基于Adaboost-PSO-BP模型的开采沉陷预测研究

邢 垒，原喜屯，张 沛

(西安科技大学，陕西 西安 710000)

开采沉陷是矿物被开采后，岩体中原始应力平衡状态改变，使地表和岩层产生连续移动、变形和非连续破坏的现象[1]。大面积矿物开采导致区域环境污染和资源破坏，引起开采区岩土体位形变化，诱发各种地质灾害[2]，严重影响工矿区经济发展和环境保护，威胁人民生命财产安全，阻碍工矿区和工矿城市可持续发展。因地质采矿条件复杂，传统的经验法、理论模型法及影响函数法等方法[3]仅用数学或力学理论无法对开采沉陷进行准确、全面的预测；而反复建立地表移动观测站，耗时费力又不能完全满足矿区持续生产需求[4-6]。因此通过优化算法对开采沉陷进行预测具有一定的理论与实用价值。

BP(Back Propagation)神经网络作为目前应用最广的神经网络之一，已广泛应用于开采沉陷变形预测中，并拥有良好的预测效果[7]。麻凤海、王泳嘉、范学理等把神经网络理论应用到开采沉陷中，并利用神经网络对地表沉陷进行预测，取得较满意的结果[8，9]。肖波、麻凤海、杨帆等将遗传算法和误差反向传播算法相结合，训练前馈人工神经网络，并将该方法用于解决实际问题[10]。张飞、刘文生建立粒子群优化BP神经网络的地表下沉系数选取模型，该模型优化了BP神经网络收敛速度缓慢、易陷入局部极值等缺陷[11]。为更好地处理矿区沉陷复杂非线性问题，为地表沉陷引起的破坏事故提供基础预测数据，本文在前人的研究基础上，提出了改进的Adaboost-PSO-BP模型，该模型具有较强的抗过拟合能力及较高的预测精度，对煤矿的安全生产、社会经济及环境保护具有重大现实意义。

1 Adaboost-PSO-BP模型原理

1.1 粒子群算法优化BP神经网络(PSO-BP模型)

粒子群算法(Particle Swarm Optimization，PSO)通过模拟鸟类捕食行为追随当前最优值寻找全局最优。更新公式：

vi=wvi+c1rand()(pbesti-xi)+

c2rand()(gbesti-xi)

(1)

xi=xi+vi

(2)

式中，i=1，2，…，N，N是粒子的总数；vi是粒子的速度；w是惯性权重，其值为非负；c1和c2是学习因子，通常取值为2；rand()是介于(0，1)之间的随机数；pbest为粒子当前个体极值；gbest为整个粒子群共享全局最优解；xi是粒子当前位置。

1986年，以Rinehart为首的科学家们提出一种多层前馈网络BP神经网络，其是用误差逆传播算法不断调整网络权值和阈值，使误差最小。

PSO算法具有全局搜索性能及鲁棒性高等特点，可用于优化BP神经网络，具体步骤如下[12]：

1)设置BP神经网络参数，建立BP神经网络，初始化其权值及阈值；

2)设置PSO算法参数，其中粒子维数H计算公式为：

H=hj+hjhi+hjhk+hk

(3)

式中，hj是BP神经网络的输入层数；hi是BP神经网络隐层层数；hk是BP神经网络输出层数。

3)以BP神经网络的均方误差作为适应度函数，计算公式为：

式中，N、H分别为样本个数和粒子维数；yij、Yij为样本i对应的理论输出和实际输出。

4)用PSO算法不断搜索全局最优解，使适应度值达到最小，确定权值、阈值。

5)用BP神经网络再次训练，建立PSO-BP模型。

1.2 Adaboost-PSO-BP模型

1990年Schapire最早提出Boosting算法，能提高任意学习算法精度。之后Freund和Schapire将其改进为Adaboost算法，使其更容易处理实际问题[13]。Adaboost 算法的核心思想是将误差大的训练样本权重增大，重新分配权重进行训练，利用多个弱预测器组成强预测器。本文以PSO-BP模型为弱预测器对训练样本训练、预测，将输出预测误差大于预定误差的样本作为加强训练样本，调整其权重，以改变之后的权重计算下一个弱预测器的权重，多次训练后，可得到多个弱预测器及其权重，组合成强预测器进行预测，输出预测结果[14]。

Adaboost-PSO-BP模型预测具体步骤如下：

设训练数据集中存在m组训练样本[x1，x2，…，xm]：

1)初始化训练数据集中m组训练样本权重wi：

式中，wi为初始权重；m为训练样本数。

2)确定PSO-BP弱预测器个数N，对训练样本训练、预测。

3)计算训练样本的预测误差ec。

4)调整训练样本权重wi，并进行归一化。

式中，i=1，2，…，m；ec是预测的误差绝对值；ee为预定误差限值。

5)计算第t个PSO-BP弱预测器的预测误差率et。

et=∑wii=1，2，…，m；t=1，2，…，N

(7)

式中，N为弱预测器的个数。

6)计算第t个PSO-BP弱预测器的权重at：

式中，N为弱预测器的个数。

迭代N次后停止训练，否则返回(2)。

7)合成Adaboost-PSO-BP强预测器。经N次训练，根据权重将N组弱预测函数ft(x)加权组合成强预测函数F(x)。

2 实验分析

2.1 实验数据

采空区地表沉陷规律因影响因素取值不同而表现出较大差异性，为提高预测模型的泛化能力，本文选取影响因素取值各异的32组数据作为样本数据[15]，主要影响因素确定为覆岩平均单向抗压强度、煤层倾角、采深、采厚、工作面尺寸、松散层厚度、推进速度，其中，以覆岩平均单向抗压强度表示覆岩力学性质对地表沉陷的影响；以松散层厚度表示松散层对地表沉陷的影响。样本数据见表1。

表1 样本数据

2.2 模型建立

以表1中前27组数据作为训练样本，后5组数据作为测试样本。因3层BP神经网络预测结果能够逼近任意非线性函数[16]，故采用3层BP神经网络对矿区最大下沉值进行预测，将表1中下沉影响因素作为输入层、地表最大下沉量作为输出层，即输入层和输出层节点个数分别为7和1，根据Kolmogorov定理，隐含层节点数范围是[4，13]，经重复测试，结果表明：隐含层节点数为7，拟合效果最佳，根据式(3)可得粒子维数为64；此外，种群规模为50，进化次数为300，学习因子为2，惯性权重取值为[0.5，1]梯度下降。

本文基于MATLAB软件，分别建立了由Adaboost算法改进的BP模型(Adaboost-BP模型)以及进一步优化的Adaboost-PSO-BP模型，两模型中的弱预测器个数为9，分别对测试样本进行预测。实验中BP模型和PSO-BP模型各进行了9次预测，结果如图1所示，图1预测值均指其误差均值。

图1 实验预测结果

2.3 结果与分析

模型绝对误差对比见表2。从表2中数据可知，优化后各模型预测结果都优于传统BP模型，BP模型绝对误差值最小值-293.28mm，最大值达到426.71mm；Adaboost-BP模型绝对误差值最小值54.23mm，最大值78.54mm；PSO-BP模型绝对误差值最小值41.89mm，最大值160.3mm；故以Adaboost算法和PSO算法分别对BP模型优化已取得较好结果，都适用于对开采沉陷的预测；而Adaboost-PSO-BP模型绝对误差值最小值只有35.41mm，预测效果更好。

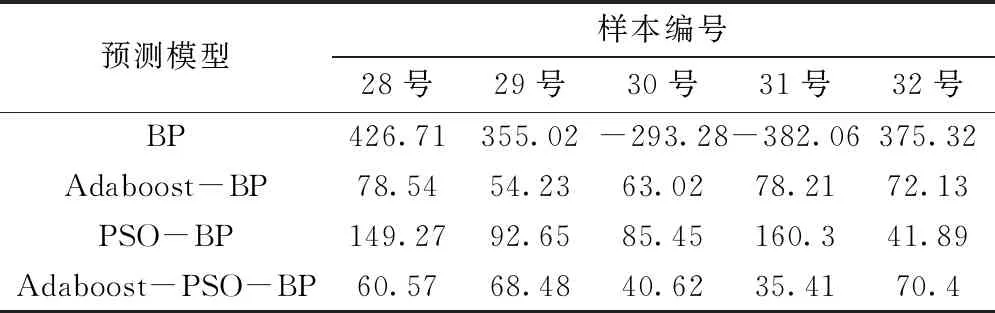
表2 模型绝对误差对比 mm

注：BP、PSO-BP两模型的误差绝对值为9次预测误差的均值。

模型相对误差对比见表3。由表3中数据可知，由于传统BP网络泛化能力差，易陷入局部最小值，故其预测精度最低，相对误差值最高到40.73 %；粒子群算法克服BP算法局部最优的缺陷，提高局部区域的收敛速度，通过惯性权重协调全局搜索与局部搜索，以较大概率保证最优解，经粒子群优化的BP模型精度有较大改善，平均相对误差达到7.24%；由Adaboost算法改进的BP模型预测精度相较于PSO-BP模型平均相对误差精度提升到5.16%；本文改进的Adaboost-PSO-BP模型的精度最高，平均相对误差只有4.26%。Adaboost算法在优化BP模型时的精度已优于PSO-BP模型，进一步改进的Adaboost-PSO-BP模型精度再次提升，表明该模型根据预测误差调整若干组弱预测器之间的权重，将神经网络不同的预测结果加权平均，组成强预测器，实现了 “优中选优”的目标。

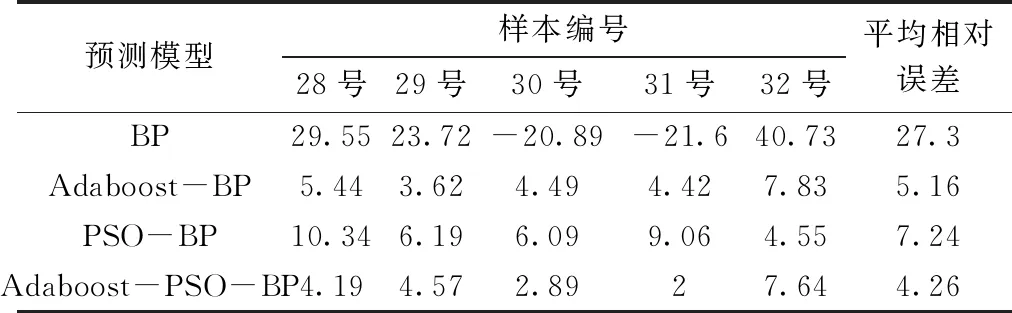
表3 模型相对误差对比 %

3 结 论

经传统BP模型、Adaboost-BP模型、PSO-BP模型及Adaboost-PSO-BP模型精度对比，结果表明：由于标准BP模型初始阈值和权值是系统任意分配，故预测结果具有不确定性；Adaboost-BP模型和PSO-BP模型分别通过侧重预测误差大的样本和优化神经网络权值及阈值的方法，弥补了BP模型的缺陷，在预测精度上有一定程度的提高；而本文提出的Adaboost-PSO-BP强预测模型同时融合Adaboost算法和PSO算法的优势，进一步提升了预测精度，证实了Adaboost-PSO-BP强预测模型在开采沉陷预测中的可行性和实用性。但网络稳定性问题，仍需进一步研究。