一种槽口与永磁体组合偏移的永磁同步电机齿槽转矩削弱方法

刘 婷，杨国灵，邓秋玲，谢 雅

（1.湖南工程学院 电气与信息工程学院，湘潭 411104；2.湖南工程学院 计算机与通信学院，湘潭 411104）

0 引言

随着我国经济发展与科技的不断进步，永磁同步电机因其诸多优点在航空航天、工农业、新能源、生产生活等领域应用十分广泛.而存在于永磁电机内的齿槽转矩，是影响永磁电机输出性能的一个重要参数.由于电机一般都有定子齿槽结构，电机永磁体与定子齿槽之间相互作用力的切向分量引起齿槽转矩.目前已有的永磁同步电机齿槽转矩优化方法主要分为两大类：一种是包括优化极槽配合选择、永磁体极弧系数优化、定子槽口宽度优化等的优选电机参数法；另一种是包括磁极偏移、斜极、辅助槽、不等齿宽和不等槽口宽等的改变电机结构法［1-4］.

近年来有学者对这两种方法进行了研究，文献［5］、［6］提出了基于电机重复单元的磁极偏移齿槽转矩削弱方法，文献［7］提出了槽口偏移的方法.两种方法都可通过消除齿槽转矩中多次高次谐波达到优化齿槽转矩的目的.但槽口偏移方法在一定程度上受到槽宽的限制，由于电机的齿宽是有限的，有时槽口能实际偏移的角度小于通过理论计算出的偏移角度，而达不到理想的齿槽转矩削弱效果.永磁体偏移方法会使部分磁极间距变近，导致磁极的端部漏磁增加.本文提出了一种采用永磁体偏移和槽口偏移组合来消除多次齿槽转矩谐波的齿槽转矩削弱方法，并采用有限元仿真进行验证.使用该方法一方面可减小磁极偏移幅度过大带来的漏磁增加；另一方面可解决槽口偏移方法偏移位置受限的问题.

1 原理分析

1.1 齿槽转矩计算的基本原理

齿槽转矩即当电机的定子和转子之间发生相对运动，永磁同步电机的定子绕组在不通电情况下也存在转矩.电机磁场能量可表示为：

W为磁共能；α为某个永磁体位置与某个电枢齿位置的夹角.

当不考虑电机的电枢铁心饱和，同时假定铁心的磁导率为无穷大时，可以将电机中所储藏的磁场能量W看成永磁体中储藏的磁场能量和电机气隙中储藏的磁场能量之和：

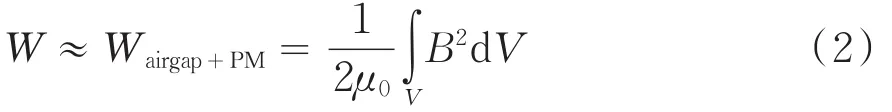
μ0为空气磁导率.在电枢圆周面上的气隙磁密可近似表示为：

在磁极中心线上,θ=0.Br为永磁体剩磁磁密；hm为永磁体磁化方向长度；g为有效气隙长度.

对Br2(θ)和进行傅立叶分解及变形可得：

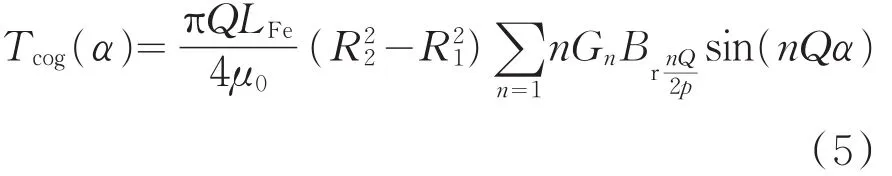
LFe为定子铁心长度，R1为转子外半径，R2为定子轭内半径，Q为定子槽数，p为极对数，n为一个使得nQ/2p为整数的整数.

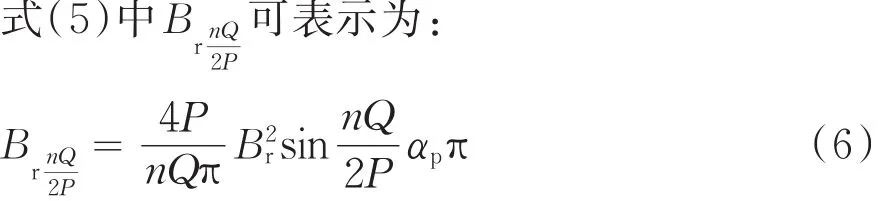
1.2 磁极偏移原理

根据已有的研究成果，电机每一个磁极作用下产生的齿槽转矩都是一系列正弦波的叠加，第j个磁极对应的齿槽转矩为［5-6］：

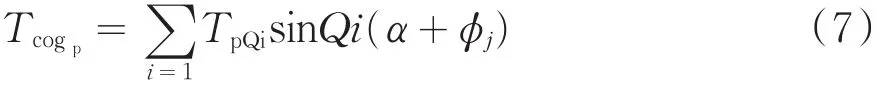
TpQi为一个永磁体产生齿槽转矩对应的傅立叶系数；α+φj为第j个永磁体位置与电枢齿位置的相对角度.当j=1时，φ1=0，永磁体与电枢齿相对位置角为α.

假定永磁磁极的端部相距很远，整个电机的齿槽转矩可基本看作由各永磁体单独作用下齿槽转矩之叠加和.电机总齿槽转矩可表示为：

由于电机整体的齿槽转矩为所有永磁体单独作用下产生齿槽转矩的叠加，因此若将永磁体进行合适角度的偏移，可达到削弱齿槽转矩谐波的目的.

1.3 槽口偏移原理

根据已有研究成果，当电机不是斜槽时，电机每个定子槽作用下产生的齿槽转矩都可表示为傅里叶级数的形式，第j个定子槽对应的齿槽转矩为［7］：

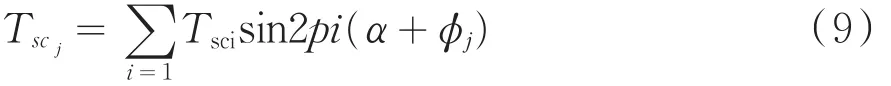
Tsci为单个定子槽产生齿槽转矩对应的傅立叶系数；α+φj为第j个定子槽位置与转子位置的相对角度，其中(j-1).当j=1时，φ=0，定子1槽与转子相对位置角为α.

电机总的齿槽转矩可表示为：

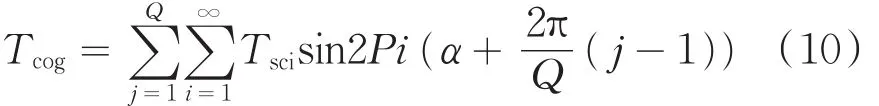
由于整个电机的齿槽转矩为各定子槽单独作用下产生齿槽转矩之和，因此若将定子槽口进行合适角度的偏移，可达到削弱齿槽转矩谐波的目的.

2 电机模型选择

本文选取一台1.8 kW永磁同步发电机为研究对象，对电机进行初步设计，部分参数如表1所示.建立模型如图1所示.

表1 电机模型参数

表1 （续）

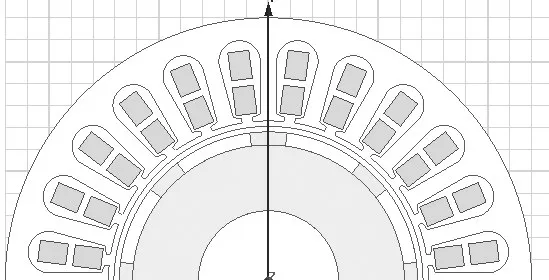
图1 电机原始模型（8极24槽）

3 有限元仿真验证

3.1 磁极偏移

文献［5］提出了永磁体偏移角度的理论计算公式，根据公式可得各永磁体的偏移角度.本文采用8极24槽模型，将所有永磁磁极顺序编号命名为P1～P8，根据表2可分两步进行磁极偏移，采用“偏移角度1”所在列的偏移方式可消除齿槽转矩基波，在“偏移角度1”基础上进一步进行“偏移角度2”所在列的偏移方式可进一步消除2次谐波.磁极偏移后电机模型如图2所示，图3为仿真结果对比.

表2 磁极偏移角度

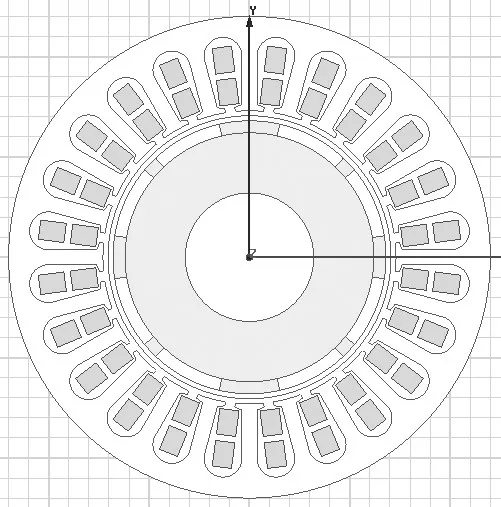
图2 磁极偏移模型（8极24槽）

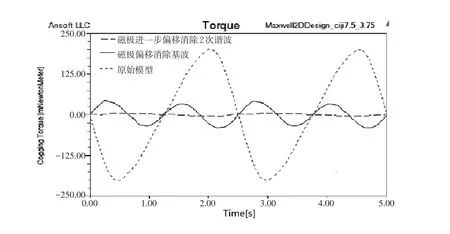
图3 原始模型与磁极偏移模型齿槽转矩对比

从图3来看，原始模型所得齿槽转矩仿真曲线每个定子齿距内有一个周期的齿槽转矩，幅值为200.6 mN·m.采取表2中“偏移角度1”所在列对应的方案消除基波后，仿真波形频率为原始波形的2倍，幅值为43.05 mN·m，减小了78.5%，在此基础上进一步按“偏移角度2”偏移相应磁极，此时基波和2次谐波同时被消除，齿槽转矩幅值减小至5.6 mN·m，与原始模型相比减小了97.21%.

3.2 槽口偏移

文献［7］提出了槽口偏移的理论计算公式.根据公式可得各槽口偏移角度.本文采用8极24槽模型，将所有电机槽口顺序编号命名为Q1～Q24，相邻的3个槽口为1组，以组为单位进行偏移.表3为根据理论计算得到的槽口偏移角度方案.根据其中“偏移角度1”所在列的偏移方案可消除齿槽转矩基波.在此基础上进一步进行槽口“偏移角度2”方案的槽口偏移可进一步消除2次谐波.由于本文模型电机定子槽宽的限制，每个定子齿槽所对应的空间角度只有15°，对槽口进行最大限度偏移，定子槽口可偏移的空间约为3.37°.此处用偏移角度3.37°代替“偏移角度1”中的3.75°进行偏移，槽口偏移后电机模型如图4所示，仿真结果对比如图5所示.

从图5来看，采用原始模型一个定子齿距内有一个周期的齿槽转矩，幅值为200.6 mN·m.采用3.37°代替“偏移角度1”中的3.75°进行偏移后，幅值为131.7 mN·m，减小34.34%，不能完全消除基波.

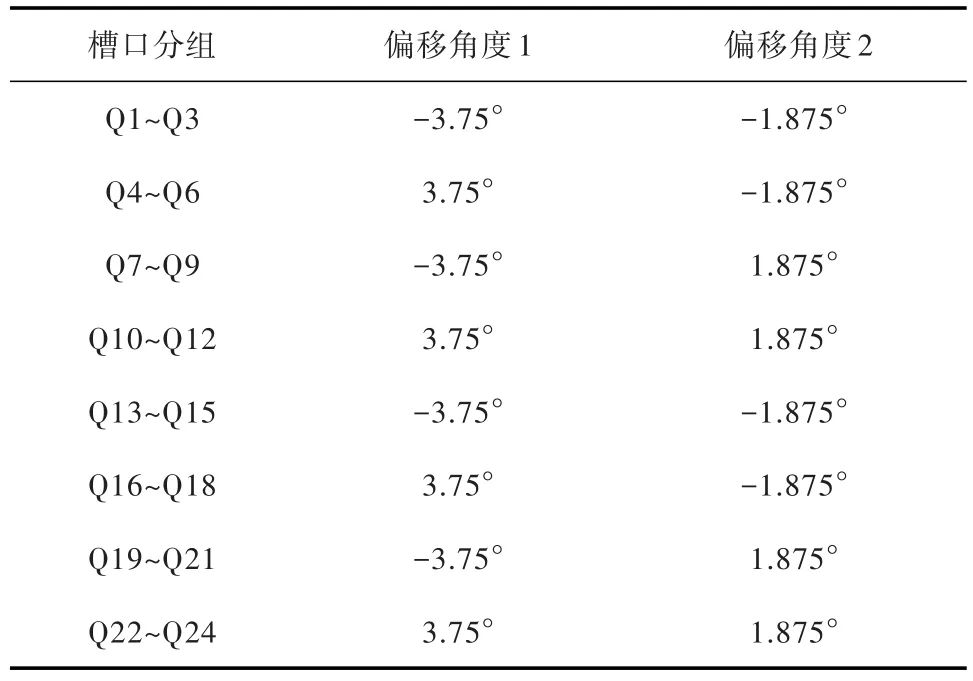
表3 槽口偏移角度

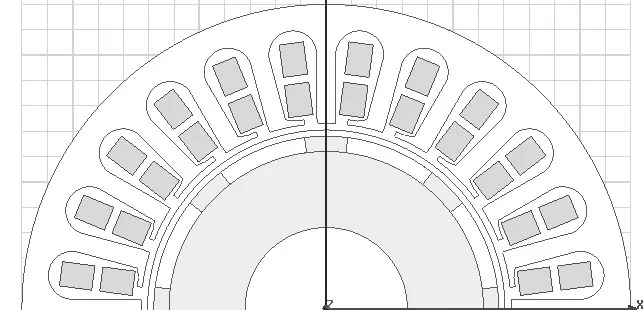
图4 槽口偏移模型（8极24槽）

图5 原始模型与槽口模型电机齿槽转矩对比

3.3 磁极偏移与槽口偏移组合

考虑组合应用磁极偏移与槽口偏移的方法，在磁极偏移消除电机基波的基础上使用槽口偏移进一步消除2次谐波，组合偏移方法如表4所示，电机经过组合偏移后模型结构如图6所示，仿真结果对比如图7所示.

从图7来看，原始模型齿槽转矩大小为200.6mN·m.采用磁极偏移磁极消除了基波以后，齿槽转矩仿真波形的频率为原来的2倍，幅值降低至43.05 mN·m，减小了78.5%，在磁极偏移基础上进一步对槽口组按表4进行偏移消除2次谐波后，仿真波形幅值降低至15.05 mN·m，与原始模型相比减小了92.5%.

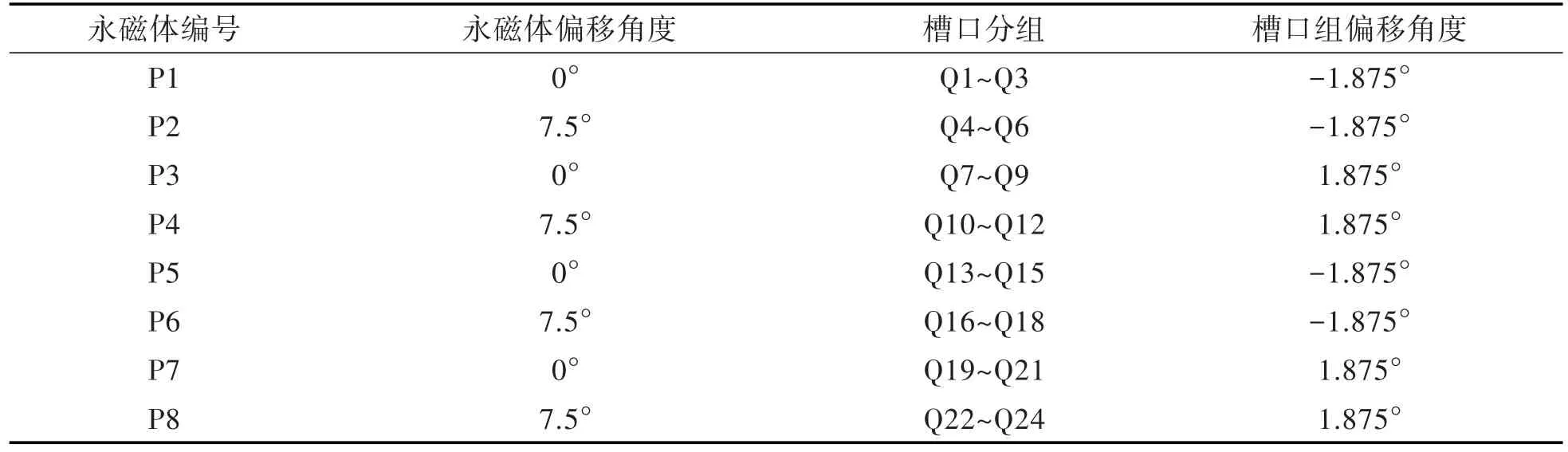
表4 组合偏移方法

图6 组合偏移方法模型（8极24槽）

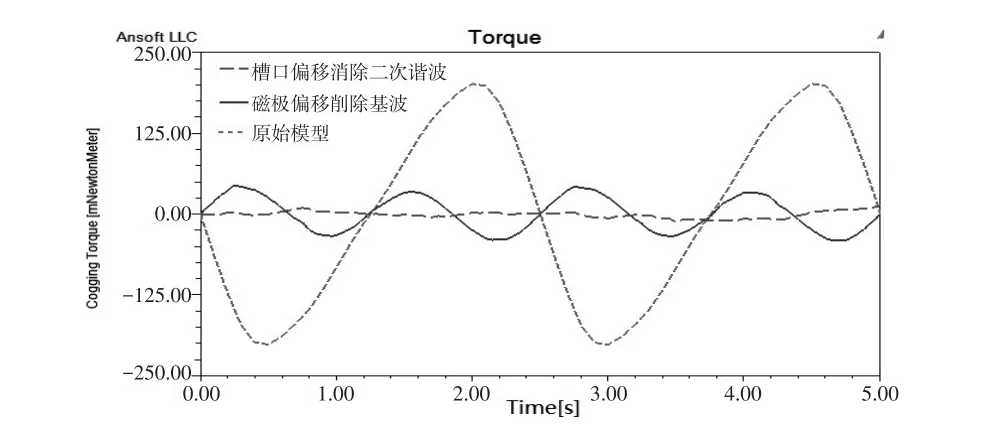
图7 原始模型与组合偏移方法模型齿槽转矩对比

4 结束语

本文提出了一种采用磁极偏移和槽口偏移两种方法组合，用以削弱电机齿槽转矩中的基波与2次谐波，建立模型进行有限元仿真，仿真结果验证了采用此组合偏移方法齿槽转矩削弱效果显著.

由于磁极偏移会使部分磁极间的间距变小，增大漏磁，另外电机齿槽宽度有限，槽口偏移方法受到槽宽的限制，本文使用磁极偏移方法消除基波，再配合槽口组偏移消除2次谐波，达到显著的削弱齿槽转矩效果.与仅使用磁极偏移或槽口偏移方法中一种方法相比，可减小磁极偏移和槽口偏移角度，减小漏磁和齿槽宽度限制槽口偏移角度的影响.若电机中槽口偏移位置足够，也可考虑采用偏移槽口组消除基波配合偏移磁极消除2次谐波的方法.