基于NTRU格的云数据可撤销属性基加密方案

江健豪 蒋 睿 裴 蓓 吴松洋

(1东南大学网络空间与安全学院，南京210096)(2信息网络安全公安部重点实验室，上海200031)

云计算通过互联网为用户提供大量虚拟资源和技术，减小用户在本地的存储和计算开销，同时对数据批量处理从而方便用户进行数据访问.然而，云环境的公开性使得数据极易遭受攻击.因此，应用在云环境中的加密算法需要保证仅有符合条件的用户能够完成数据解密，并防止云服务器直接获取数据内容.同时，加密方案需要更高效的密钥分发与更新以满足用户身份的复杂性和用户权限注册与注销带来的高流动性.由于云数据的数量大且种类繁多，需要根据用户需求提供细粒度的数据访问服务，同时保证数据的机密性.因此常规的加密算法无法针对云数据的这一特点实现安全加密.

为了进行细粒度的数据访问控制，Sahai等[1]和Shamir[2]提出属性基加密方案(attribute-based encryption, ABE).Bethencourt等[3]在此基础上提出密文策略属性基加密方案(ciphertext-policy ABE, CP-ABE)，其相对于密钥策略属性基加密方案[4]更适合于云数据加密.如果需要撤销CP-ABE方案中某个用户的属性以改变该用户访问权限，需要解除该用户对这些属性相关密文的访问权限并保留其他合法用户的数据访问权限.为了实现属性的安全撤销，Chang等[5]通过云服务器的重加密进行属性撤销，但任何撤销都会影响系统的所有属性，效率较低.文献[6]中的方案能够同时实现安全撤销并抵御共谋攻击，但同样运行效率较低；文献[7]通过引入属性群组的概念改进了效率.文献[8]中的方案通过用户群组管理员解决属性撤销的问题.Xiong等[9]提出了通过动态身份群组简化访问结构，实现属性撤销并保护用户隐私.文献[10]中的方案实现了数据删除和属性撤销.然而，目前已经出现有效运算离散对数的量子算法[11].以上方案均不能抵御量子计算攻击，需要应用新的抗量子计算加密算法来抵御潜在的量子计算攻击.

格难题是量子计算机不擅长解决的一类传统数学领域上的问题，主要包括最短格问题(shortest vector problem, SVP)、误差学习(learning with error, LWE)难题等，这些难题被证明在量子计算攻击下是难以解决的.由于格问题存在最坏情况到一般情况的困难性规约[12]，降低了算法对困难性假设要求，因此出现了大量基于格的公钥加密算法[13-14].Gentry等[15]基于LWE难题构建了原像采样陷门函数，并将其运用在数字签名和IBE方案中，文献[16]优化了这种陷门函数生成的采样向量长度.Hoffstein等[17]基于近似最短向量问题提出了NTRU(number theory research unit)算法，提高了格加密算法的效率.Stehlé等[18]将NTRU算法与环上误差学习问题(learning with error problem over ring, R-LWE)的困难性联系在一起，证明了密钥多项式生成的公钥具有均匀随机性，给出了标准模型下的安全性证明.

为了实现加密云数据抗量子计算攻击的性能，一些学者致力于将传统ABE方案与格加密算法相结合，构造基于格加密算法的ABE方案.文献[19]提出了一种理想格上的ABE方案，然而该方案既不能防止共谋攻击也不能进行属性撤销.文献[20]提出了一种可以防止共谋攻击的基于格的ABE方案，但同样不能够实现属性撤销.文献[21]改进了访问控制结构，优化了属性分配方案，但是同样未能实现安全的属性撤销.文献[22]将改进的陷门函数应用于ABE方案中，提高了计算效率，但仍然未考虑到属性撤销.文献[23]采用二叉树结构，通过罗列所有属性和用户集生成接入结构，并采用加密算法生成对应所有接入结构的重复密文，最后以此方式实现属性撤销；该方案运算量远大于一般的属性集加密算法，没有实现真正意义上的属性撤销，无法适用于外包的云存储.文献[24]采用二叉树结构实现属性撤销，并基于拉格朗日多项式实现门限访问策略；然而该方案的缺陷在于属性被撤销的用户仍能解密撤销前上传到云服务器的密文，并且基于属性二叉树的属性撤销的单次撤销运算量比重新初始化系统更大.文献[25]结合文献[24]的重加密方案，通过二叉树结构生成属性用户群密钥并进一步更新用户私钥，以此解密外包服务器重加密后的密文；然而，该方案的缺陷在于未对撤销前存储在云服务器的密文进行更新，无法实现安全的属性撤销.文献[26]基于R-LWE问题，通过构造陷门函数产生属性私钥，并结合属性基加密算法提出一种具备抗量子计算攻击的云数据外包加密方案；该方案可实现有效的用户属性撤销，但密钥尺寸庞大，运算效率较低.

除文献[26]外，目前基于格难题的属性基加密方案均不能实现真正意义上的有效属性撤销.为抵御量子计算攻击并解决安全属性撤销问题，同时进一步提高运算效率，本文提出一个属性可撤销的抗量子计算攻击CP-ABE方案RNL-ABE(revocable NTRU lattices based attribute-based encryption).首先通过构建NTRU格并从中采样生成属性公私钥对，将R-LWE难题与CP-ABE方案结合，实现了密钥的安全保护，形式化地证明了该方案在选择属性集模型下能够抵御量子计算攻击；同时，实现了云数据的细粒度访问控制和高效安全的属性撤销，并且防止云中各类实体间实施共谋攻击.

1 预备知识

1.1 NTRU格的相关定义和定理

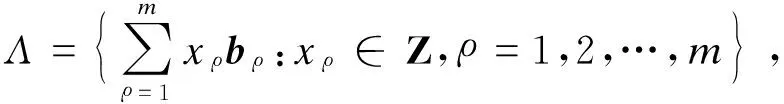
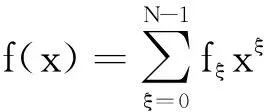
定义4(判定性小多项式商假设(decisional small polynomial ratio assumption，DSPRφ,q,χAssumption) 设φ(x)∈Z[x]为一个n阶多项式，质数q∈Z，χ为环R≜Z[x]/φ(x)上的分布，那么从分布χ中采样的多项式f,g的商h=g·f-1modq(假设f在环Rq=R/qR中可逆)和从Rq上均匀随机采样的多项式是不可区分的[13].

1.2 离散高斯分布

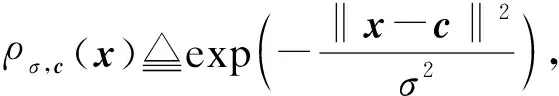
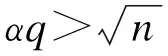
1.3 环上的误差学习问题

定义6(判定性R-LWE) 对于定义2中环Rq=Zq[x]/(xN+1)，q=1mod(2N),a∈Rq为均匀随机选取的向量，s∈Rq为秘密向量，e∈R为服从定义5中离散高斯分布Ψα的误差向量.令环上向量b=a·s+e,b∈Rq，判定性R-LWE问题是区分向量组(a,b)与R2上均匀随机选择的向量组[14].

根据定义6，定义关于判定性R-LWE问题的随机预言机Ω.

定义7(随机预言机模型) 随机预言机Ω将以同等的概率通过如下定义的2个采样器中进行采样.

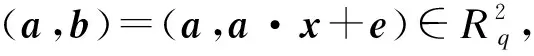
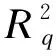
判定性R-LWE问题允许敌手多次询问预言机Ω，并且根据得到的采样给出对于采样器的猜测Ωr，r∈{1,2}.由于判定性R-LWE问题是困难的，任何敌手对Ω的猜测Ωr所具有的优势Pr[r=1]-Pr[r=2]都是可忽略的.

1.4 选择属性集模型

定义8(选择属性集安全模型) 对于CP-ABE的选择属性集模型 (selective-set model)[28]定义如下.

①在初始化阶段，敌手V公布访问策略A.

②在启动阶段，挑战者运行CP-ABE方案的启动算法生成公共参数并发送给敌手.

③在询问阶段，允许敌手V对不同的属性集合Sj中的属性询问对应私钥，但V挑战的属性集Sj中的属性不包含在访问策略A中.

④在挑战阶段，敌手V提交2个等长消息M0和M1.挑战者抛掷硬币c∈{0,1}，根据结果选择消息Mc加密后发送给敌手V.

⑤重复询问阶段.

⑥在猜测阶段，敌手V对c返回猜测c′.敌手V在这个游戏中具有优势Pr[c′=c]-1/2.

1.5 属性撤销安全模型

定义9(属性撤销安全模型) 属性撤销安全模型定义如下.

①在初始化阶段，敌手V公布目标访问策略、自身属性集S和撤销属性集Sr.撤销属性集Sr是属性集S的子集.

②在启动阶段，挑战者运行CP-ABE方案的启动算法并生成私钥发送给敌手V.

③在询问阶段，敌手V从集合SSr中选择属性j*，挑战者撤销属性j*，生成相关更新组件并发送给敌手V.

④在挑战阶段，敌手从撤销属性集合中选择属性j，挑战者抛掷硬币c∈{0,1}.若c=0则随机生成密文发送给敌手V.若c=1则撤销属性j，将更新后的密文发送给敌手V.

⑤重复询问阶段.

⑥在猜测阶段，敌手V对c返回猜测c′.敌手V在这个游戏中具有优势Pr[c′=c]-1/2.

2 基于NTRU格的可撤销属性基加密方案

2.1 系统模型

系统模型如图1所示，共5个实体.

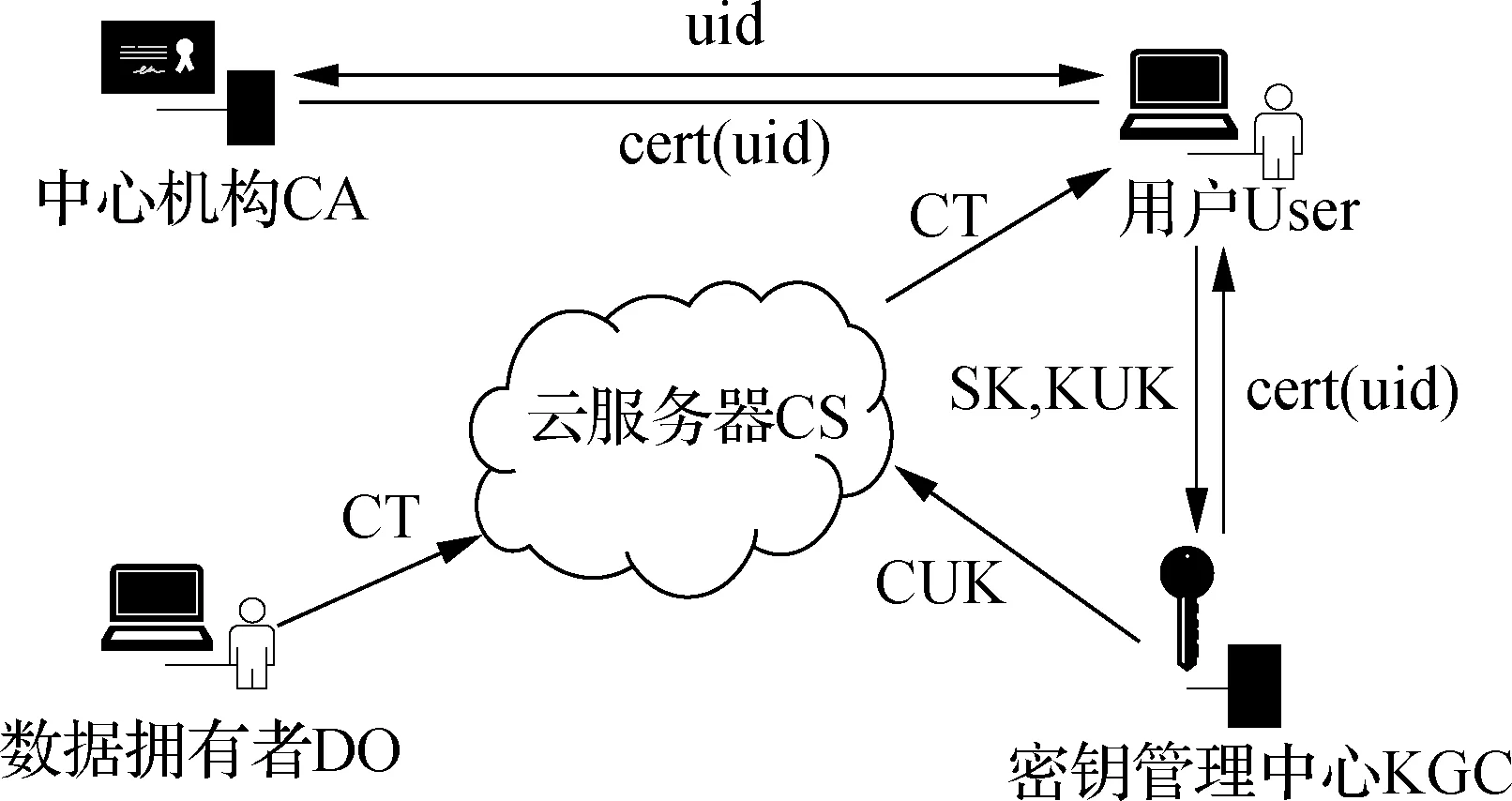
图1 系统模型

证书颁发机构(CA)是一个全局可信的中心机构，每个用户需要向CA发送身份信息进行注册.在CA确认用户合法性后，向用户发送对应证书，便于用户在之后的过程中证明自己的身份.

密钥管理中心(KGC)是一个管理用户属性和密钥的权威机构.用户在CA注册后可以向KGC请求密钥，KGC收到用户发送的证书后，将对应的属性分配给用户并为其生成对应的密钥.KGC同时负责属性撤销并更新用户密钥.

云服务器(CS)为用户提供存储数据的空间，接收需分享的加密数据.当KGC执行属性撤销时，CS可从KGC接受更新信息，进行密文的更新.

数据拥有者(DO)指的是部分提供上传数据的用户.他们可以自己决定上传数据的访问策略，并将其嵌入密文进行加密.

用户根据自身需求从CS下载加密数据，当用户属性满足访问策略时可以成功解密.

2.2 威胁模型

本文方案定义威胁模型中共有6个实体：证书颁发机构(CA)、密钥管理中心(KGC)、云服务器(CS)、合法用户、属性被撤销的用户和外部攻击者.CS是诚实但好奇的，它始终正确地执行方案中所有实体提出的要求，但会试图解密密文内容；CA和KGC为诚实可信的，意味着它们始终正确地执行方案中所有实体提出的要求，并且不会对密文密钥等秘密内容好奇；合法用户是唯一有权利通过方案规定的合法途径进行解密的实体；属性被撤销用户是指某个属性已经被撤销，因而对该属性相关的密文失去了访问权限的用户，他们仍然会试图解密这些密文；外部攻击者是指没有密钥并试图解密密文的非法入侵者.

在本文的威胁模型中，合法用户、属性被撤销用户以及外部攻击者3方都可以相互交换部分信息，进行共谋攻击.

2.3 RNL-ABE方案

2.3.1 系统初始化

在系统初始化阶段共有如下3个步骤：CA启动、KGC启动、生成系统公钥和密钥.

1) 在CA启动阶段，CA根据系统安全参数λ选定多项式阶数N、模数q以及一个较小的质数p≪q.随后每个用户将他们的身份信息发送给CA.在确定了用户身份合法之后，CA随机选择一个uid∈Zq作为用户唯一身份标识符，然后输出证书cert(uid).最后CA定义哈希函数H将uid∈Zq映射到H(uid)∈Zq.

2) 在KGC启动阶段，KGC设定一个属性集{x1,x2,…,x|S|}, 其中|S|为本文方案中涉及的属性个数，随后为每个元素随机选择γj∈Rq作为属性参数.随后KGC通过文献[16]中的高斯采样算法Gaussian_Sampler(B,σ,c)对定义2中的格基B生成系统公钥与私钥.

3) 生成系统公钥和私钥的流程如下.

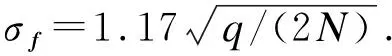
②用扩展欧几里得算法计算多项式环向量ρf,ρg∈R和Rf,Rg∈Z，满足等式

-ρf·f=Rfmod(xN+1)

-ρg·g=Rgmod(xN+1)

若gcd(Rf,Rg)≠1或gcd(Rf,q)≠1，则重新对f,g进行采样.

③对满足条件的Rf,Rg∈Z再次使用扩展欧几里得算法，计算满足uRf+vRg=1的u,v∈Z.

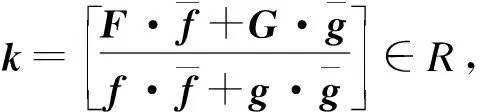
F←F-k·f,G←G-k·g

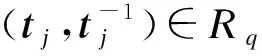
2.3.2 属性密钥生成

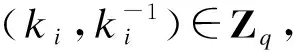
1) 输入属性参数tj，进行高斯采样(δj,1,δj,2)=(tj,0)-Gaussian_sampler(B,σf,(tj,0))，得到(δj,1,δj,2)满足{δj,1+δj,2·h=p-1tj}.

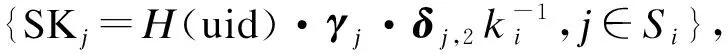
2.3.3 数据加密

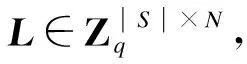
DO随机选择小多项式u∈{-1,0,1}N和e1,eφ,2∈Ψα作为误差多项式.随后将明文m∈{0,1}N设定为Nbit二进制.密文组成如下：

2.3.4 数据解密

数据解密流程如下.

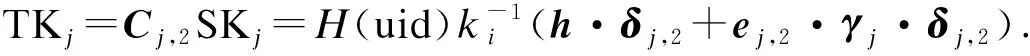
2) 解密时，符合访问路径的合法用户计算出的令牌能够进行进一步的解密得出中间量μ，即

展开TKj、Cj,1得到

进一步展开SK0，并合并式中误差向量χj=ej,2·δj，2·γj-δj，1得到

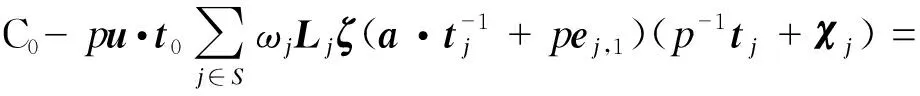
pej,1·χj)

进一步展开密文项C0=su·T0+pe1+m可得

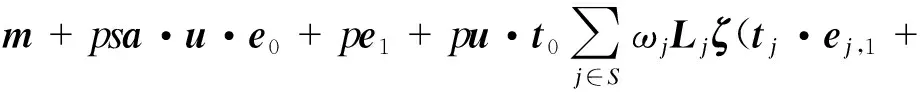
进一步计算m*=μmodp得到

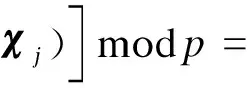
因此，可得正确的解密结果.

2.3.5 属性撤销

属性撤销流程如下.

1) 生成更新密钥时，设S′为需更新的属性集合.对属性j′∈S′，KGC随机选择γ′j′∈Rq并为每个拥有该属性的用户计算属性密钥更新密钥，即

KGC同时计算密文更新密钥：

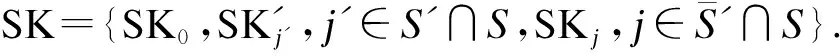
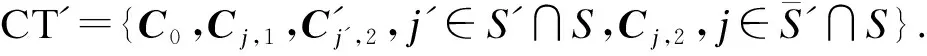
3 安全分析

3.1 正确性证明

定理1本文方案的全部加解密计算过程是正确的，即指合法用户能够成功加解密，并能实现安全的属性撤销.

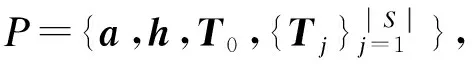
在解密的最后一步，计算得到除明文消息m以外的剩余项为

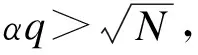
3.2 选择属性集模型下的安全证明

基于定义7中随机预言机Ω和定义8中安全模型，将证明本文方案在DSPR假设和R-LWE假设下是选择安全的，能够抵御量子计算攻击.

定理2若存在一个敌手V能够通过概率性的时间多项式(probabilistic polynomial time)算法对本文方案进行选择属性攻击，并具有不可忽略的优势ε>0，则将会存在一个概率多项式时间模拟者B以1+ε/2的概率解决判定性R-LWE问题.

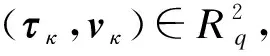
根据定义7，敌手V对于r的猜测r′具有优势为Pr[r′=r]-1/2.因此如果预言机Ω通过伪随机采样器Ω1进行采样，V对于r的猜测具有优势ε，Pr[r′=r|Ω=Ω1]=1/2+ε且Pr[Ω′=Ω|Ω=Ω1]=1/2+ε；如果预言机Ω通过随机采样器Ω2进行采样，V对于r的猜测不具有任何优势，Pr[r′=r|Ω=Ω2]=1/2且Pr[Ω′=Ω|Ω=Ω2]=1/2.

那么对于模拟者B通过敌手V对预言机进行的猜测Ω′所具备的优势为

由此定理2得证.

3.3 抗共谋攻击证明

定理3本文方案能够有效地防止合法用户和属性被撤销用户之间的共谋攻击、合法用户与外部攻击者之间的共谋攻击以及属性被撤销用户之间的共谋攻击.

证明在为用户属性生成密钥的阶段，KGC会对其选择唯一的秘密值ki∈Zq并将其绑定在用户i所拥有的属性密钥中.由于每个用户对应的ki∈Zq都由KGC保密，非法用户i*即使获取了合法用户i的密钥也不能得到属于自己的合法密钥.因此本文方案能防止合法用户和属性被撤销用户之间的共谋攻击.

同理，外部攻击者与合法用户共谋也无法伪造属于自己的密钥.因此，本文方案能够防止外部攻击者和合法用户之间的共谋攻击.

对属性被撤销的用户，其属性密钥中对应参数的值γj不变，但对应密文中Cj,2的参数γj已更新为γj′，因此属性被撤销的用户无法正确计算令牌TKj.即使他们通过共谋获取更新后的密钥SK′j，由于绑定在每个用户密钥中唯一的秘密值ki无法被替换，这些属性被撤销用户无法拥有属于自己的新的属性密钥，无法成功解密.因此本文方案能够防止属性被撤销用户之间的共谋攻击.证毕.

3.4 属性安全撤销证明

基于定义7中随机预言机Ω和定义9中安全撤销模型，我们将证明本文方案的撤销算法在DSPR假设和R-LWE假设下能够抵御量子计算攻击.

定理4如果存在一个敌手V能够通过概率性的时间多项式算法对本文方案进行选择属性攻击，并具有不可忽略的优势ε>0，那么将会存在一个概率多项式时间模拟者B以1+ε/2的概率解决判定性R-LWE问题.

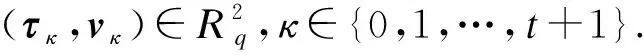
根据定义7，敌手V对于r的猜测r′具有优势Pr[r′=r]-1/2.因此如果预言机Ω通过伪随机采样器Ω1进行采样，V对于r的猜测具有优势ε；如果预言机Ω通过随机采样器Ω2进行采样，V对于r的猜测不具有任何优势.因此，模拟者B通过敌手V对预言机进行的猜测Ω′所具备的优势为

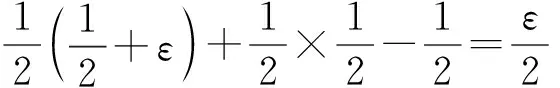
由此定理4得证.

3.5 安全性比较

我们将RNL-ABE方案与其他同类型方案[22-25,26]进行了比较，比较的目标有防止共谋攻击、安全撤销和抵御量子计算攻击.根据表1，RNL-ABE方案可以实现上述所有安全目标，而其他方案不能，因此本文方案在安全性上具有较大优势.

表1 各方案的安全性比较

4 效率分析

4.1 计算开销分析

本节进行计算开销的对比，分别比较同类型方案中加密和解密的运算量.表2为一些基于格难题的CP-ABE方案(方案1～方案5)与本文方案计算开销的对比.其中，|S|表示系统属性个数，|J|表示密文属性个数，|Si|表示解密涉及属性个数，θ表示方案3中默认属性的个数，β表示方案2中访问策略析取范式分解的子策略个数，l1=5「logq⎤,l2=6「logq⎤,l3=「logq⎤+2分别为相关文献中的陷门函数参数，mul表示环Rq上向量之间的乘法，mod表示模运算.

表2 各方案中每个实体的计算开销

4.1.1 加密开销

加密开销来源于生成密文的计算，如表2所示.RNL-ABE方案加密开销比方案1的小.这是因为方案1的访问控制涉及系统中全体属性，加密过程中需计算全体属性对应的密文组件，而本文方案只需计算密文中涉及的属性对应的组件；并且在方案1中的每1 bit明文对应的单个属性密文长度为l3bit，对应的计算量是本文方案的l3倍.因此，本方案的加密计算开销小于方案1.

同时，RNL-ABE方案的加密开销比方案2的小.这是因为在加密过程中方案2需要对密文涉及的属性进行3次环上的向量乘法计算，而本文方案仅需要进行2次；同时其属性密文长度是本文方案的l2倍，单次计算开销同样是本文方案的l2倍.另外方案2需要对β个子策略进行共β次加密，这将进一步带来数倍于本文方案的开销.因此，本方案的加密计算开销远小于方案2的加密计算开销.

相比于方案3，RNL-ABE方案的加密开销更小.这是因为在加密过程中，方案3需要进行3(θ+|J|)次向量乘法运算，而本文方案仅需要进行2|J|次运算，并且方案3的单次运算开销是本文方案的l2倍.因此本方案的加密计算开销小于方案3.

相比于方案4，RNL-ABE方案具有更小的加密开销.这是因为方案4在加密过程中需对密文涉及的属性进行4次环上向量乘法运算，而本文方案仅需进行2次，且方案4单次运算开销是本文方案的l1倍.因此本方案加密计算开销小于方案4.

最后，RNL-ABE方案加密开销比方案5的小.虽然方案5加密过程中仅需对密文涉及的属性进行1次运算，但其单次运算开销是本文方案的l2倍；而本文方案仅需进行2次运算，大多数情况下l2≫2.因此本文方案的加密计算开销比方案5小.

4.1.2 解密开销

解密开销来源于计算解密的令牌以及解密密文，如表2所示.RNL-ABE方案的解密开销比方案1的小，因为本文方案仅需要进行|Si|次的环上乘法运算，小于方案1中的|S|次，并且本文方案的单次乘法运算的开销也小于方案1.因此对比方案1，本文方案的解密开销较小.

同时，RNL-ABE方案解密开销比方案2的小，因为方案2在解密时需要进行4次环上乘法运算，相比之下本文方案仅需要进行2次环上乘法运算，并且方案2中单次解密计算的开销是本文方案的l2倍.因此对比方案2，本文方案解密开销较小.

与方案3相比，RNL-ABE方案解密开销较小.因为方案3引入了数量为θ的默认属性，在解密时需要对这些额外的属性进行3次参数计算，同时方案3单次解密运算开销是本文方案的l2倍.因此本文方案的解密开销小于方案3.

与方案4相比，RNL-ABE方案的解密开销较小.这是因为方案4在解密过程需要对用户属性进行3次环上乘法运算，而本文方案仅需要进行2次，并且方案4的单次乘法运算开销是本文方案的l1倍.因此本文方案的解密计算开销小于方案4.

最后，RNL-ABE方案解密开销比方案5小.尽管方案5在解密开销中进行环上乘法运算次数与RNL-ABE方案相同，但其单次乘法运算的开销是本文方案的l2倍.因此本文方案的解密计算开销小于方案5.

为了直观地展现计算量对比结果，通过柱状图进行展示，如图2所示.RNL-ABE方案的加解密运算量小于方案1～方案5，并减少50%以上.该结果与上文分析完全一致.

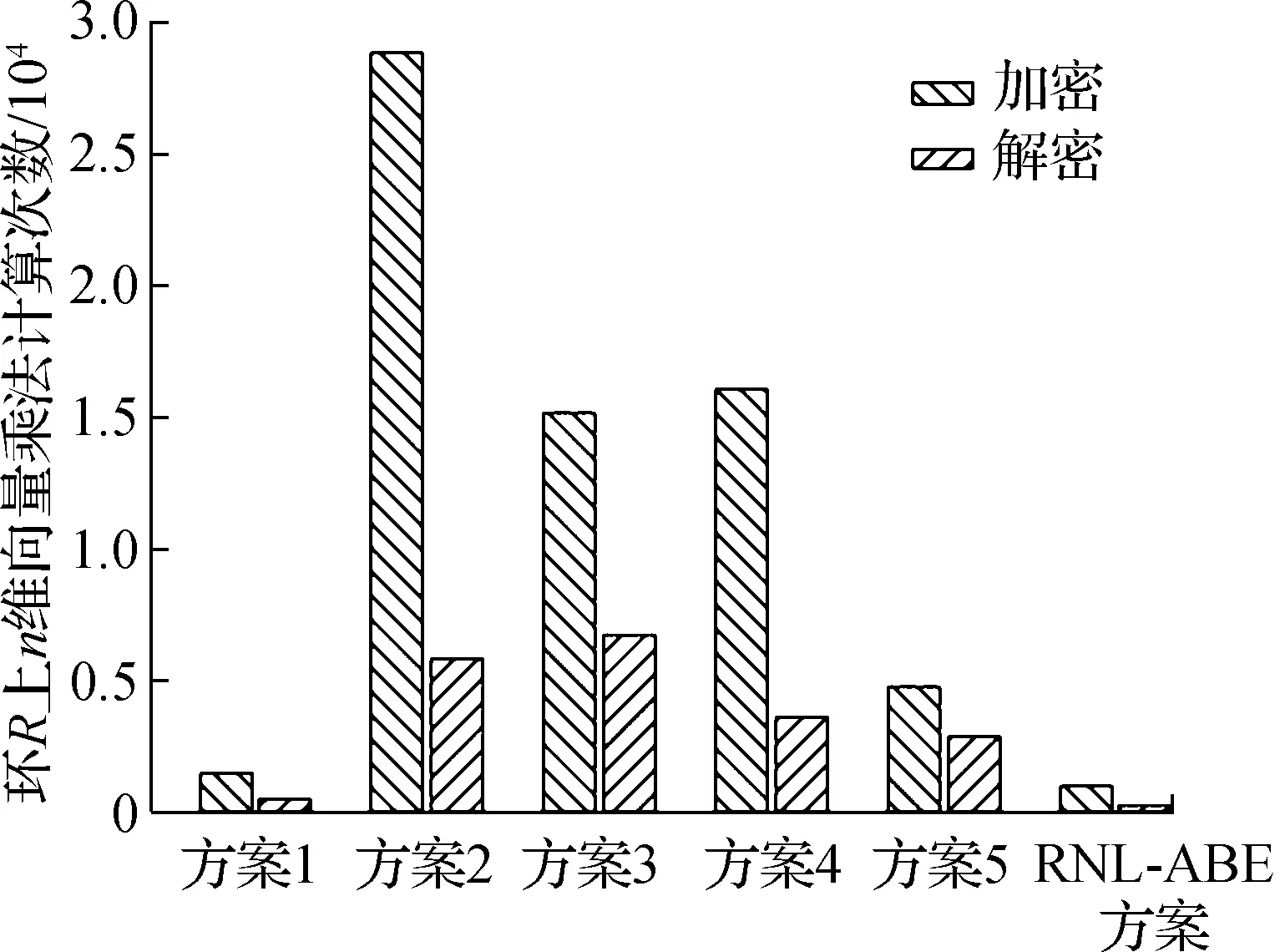
图2 各方案加解密计算量对比

4.2 通信开销分析

本节进行通信开销的对比，模拟了基于格难题的CP-ABE方案(方案1～方案5)和RNL-ABE方案的通信开销，结果如图3所示.通信开销主要来源于密文上传云服务器产生的开销.设定明文长度为256 bit的整数倍，计算明文长度从256 bit到 7 280 bit对应的密文长度，同时设置参数N=64,q=129，部分方案中陷门函数参数m1=5N「logq⎤,m2=6N「logq⎤,m3=N(「logq+1⎤+2)，方案2中析取范式分解得到的子策略个数β=10，方案3中的默认属性个数θ=10、密文涉及到的属性个数|J|=50以及系统属性总数|S|=100.

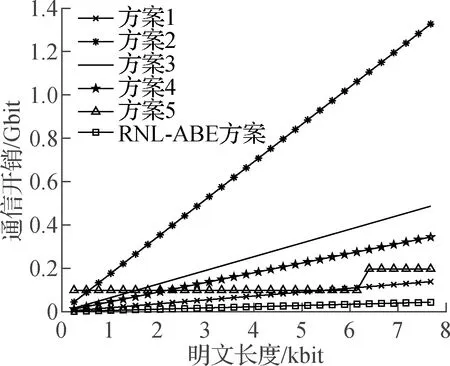
图3 各方案通信开销对比

由图3可知，RNL-ABE方案的通信开销小于方案1，这是因为方案1中与属性相关的密文采用m3×N的矩阵形式，数据量大于本文方案中的密文长度N.因此，本文方案的通信开销比方案1小.

RNL-ABE方案的通信开销远小于方案2，这是因为方案2需要对访问策略析取范式分解后的β个子策略一一加密，并且每Nbit对应单个属性密文长度为3m2，远大于本文方案的属性密文长度N.因此，本文方案的通信开销远小于方案2.

与方案3相比，RNL-ABE方案具有较小的通信开销.这是因为方案3的属性密文个数相较于本文方案多θ个，并且每Nbit对应的单个属性密文长度为3m1，远大于本文方案属性密文长度N.因此，本文方案的通信开销小于方案3.

与方案4相比，RNL-ABE方案具有更小的通信开销.这是因为方案4每Nbit明文对应的单个属性密文的长度为2m2，大于本文方案中的属性密文长度N.因此，本文方案通信开销小于方案4.

最后，RNL-ABE方案相比于方案5具有较小的通信开销.这是因为方案5需要一次性加密m2N/|S| bit(图3中对应通信开销呈阶梯上升)，平均每Nbit明文对应的单个属性密文长度为m2，大于本文方案中的属性密文长度N.因此，本文方案的通信开销小于方案5.

5 结论

1) 本文提出了一种基于NTRU格的可撤销ABE方案RNL-ABE.该方案通过R-LWE难题保证算法的安全性，同时基于NTRU格进行高效的采样和运算以保证算法的效率，并且形式化证明了RNL-ABE方案能够抵御量子计算攻击.

2) 本文方案实现安全的属性撤销并防止共谋攻击.RNL-ABE方案与已有的基于格难题的属性基加密方案相比，在解密计算开销基本相同的情况下实现了安全的属性撤销，真正实现了对云数据的细粒度访问控制，能够较好地应用于云环境中.

3) 本文方案能抵御云中各类实体共谋攻击.被撤销用户和外部攻击者无法与合法用户共谋生成自己的合法密钥，确保云存储环境中数据安全.