基于分类模型的生猪价格预测
吕逸鹏,林旭东
(华南农业大学数学与信息学院,广东广州 510642)
猪肉是我国居民餐桌上的主要肉食来源,2006 年我国猪肉产量已达5 197.2 万t[1]。受“非洲猪瘟”影响,2019 年12 月我国猪肉月均价格相比于2019 年1 月上涨了172.42%。据学者统计,不仅玉米价格、仔猪价格、“猪周期”、存栏量等因素会影响生猪价格[2-5],疫情也会长期影响生猪价格[6]。如果可以预测未来生猪价格,那么企业可以在未来价格过低时减少生猪存栏量,降低亏损,在未来价格处于较高区间时提前扩大生产,创造更多盈利。
目前众多学者常采用价格分解、经验模态分解、反向传播神经网络(BPNN)、支持向量机(SVM)、灰度模型、ARIMA 模型和向量自回归模型等深度学习和机器学习算法进行生猪价格预测、风险预警、走势分析和波动分析等研究[7-14]。较为典型的方法是使用经验模态分解将价格序列分解成不同频率,再逐个使用SVM 或神经网络算法分别进行预测[15]。另一种是使用多元回归的方法,研究影响猪肉价格的因素,再用BP 神经网络进行预测[16]。有学者使用SVM_AdaBoost 组合模型预测股票涨跌,这对本文的涨跌分类起到了启示作用[17]。本文在研究和预测生猪价格时发现,不同样本类型的预测误差是不一致的,如果将样本分成上涨样本和下跌样本,再分别进行预测,可以提高模型的效果,降低预测的误差。于是本文提出了一种基于分类模型的预测方法,利用单类样本预测误差更低这一特点,将所有样本分为下月上涨和下跌2 类,在进行生猪价格预测前,先根据日度价格数据计算出需要用于涨跌分类的各项特征,研究并提出了使用BP 神经网络和Xgboost 组合的分类模型,最后根据分类结果使用不同的多元回归模型得到生猪价格的预测值,以期为生猪企业的布局与调整提供参考。
1 材料与方法
1.1 数据来源和预处理 本文用于生猪价格预测的数据是由中国南方某养殖企业提供的从2000 年7 月1 日—2015 年11 月30 日每天的销售额和销售总重量。据此计算出每月的月初价格、最大值、最小值、月末价格和月平均价格,共计185 条数据,在此基础上画出K 线图,如图1 所示。本文根据K 线图进行上涨和下跌样本的标注,并定义将下月价格上涨的样本归类为涨样本,下月价格下跌的样本归类为跌样本。
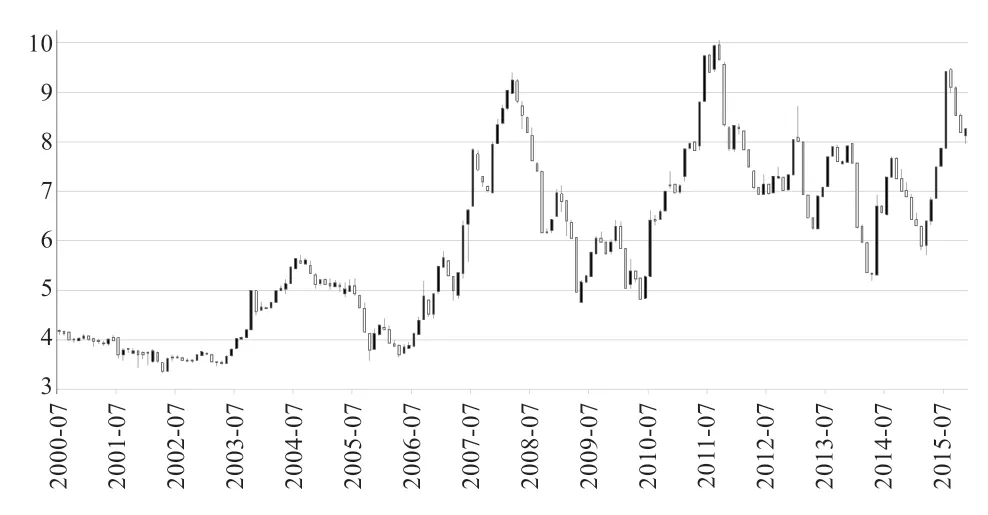
图1 生猪月度价格数据K 线图
1.2 用于涨跌分类的特征因子 样本的分类预测是整个模型的核心部分,预测样本类型的准确度直接关系到下一步生猪价格预测的误差。本文通过对比股票的涨跌相关的特点,定义了以下因素作为分类模型的候选输入特征:PMi 为第i 个月的月均价格(i=1,2,3,...,184),PD(i,j)为第i 月第j 天的日价格(j=1,2,...,30),PDi 为第i 个月最后一天的日价格,PM(max)、PM(min)为近18 个月里的最大值与最小值,PD(max)、PD(min)为近30 d 内最大值与最小值。于是第i 个月有以下指标:

其中,MD9 表示的是前8 个月和当月的MK18 的分子之和,再除以前8 个月和当月的MK18 分母之和。DD15i中n 的值为第i 个月的天数,例如当i=2 时,n=28。其中的指示价值在于当MK18 值处于MD9 值上方时,价格一般为上涨趋势,反之则为下跌,于是就有:
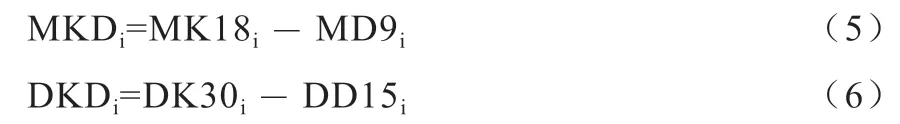
另外,本文还定义了以5 d 为单位的五日均值,1个月取6 个值,体现了第i 个月价格数据的滑动特征,以第1 个5 d 均值AVG1 为例,计算如下:
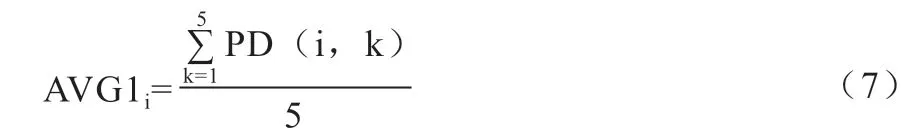
再加入月初价格和月末价格,就得到全部14 项输入特征,但只需选择其中较为重要的某些特征。本文特征因子筛选是根据Xgboost 模型中的每个因子得分的高低进行选择。此算法源自陈天奇博士论文[18],在创建决策树时,模型能根据创建时所用到的数据集中的因子,通过每个因子在分裂点改进性能的多少来计算因子的得分。将14 项特征因子输入Xgboost 模型中,得到的因子重要程度得分如图2 所示,根据Xgboost 模型的结果,选择了MK18、AVG1、MD9、MKD、DK30、DD15、DKD、AVG2 作为分类模型的输入特征,进行生猪价格涨跌分类。
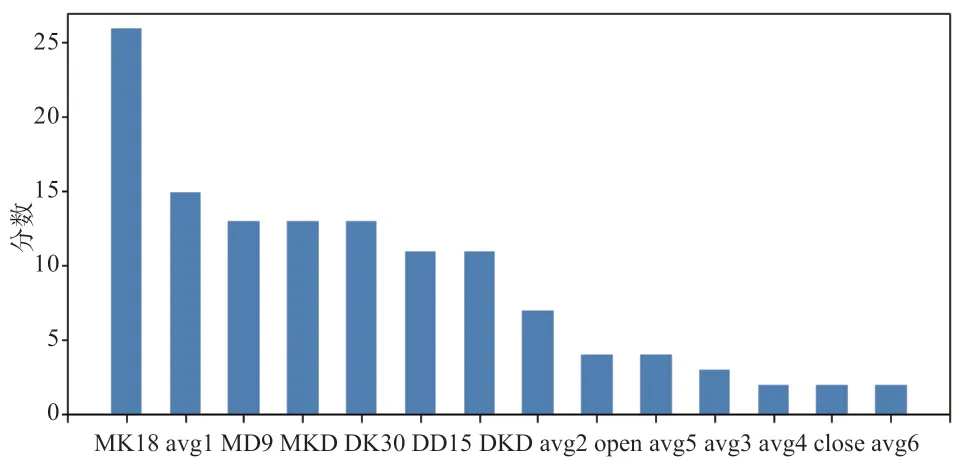
图2 各因子重要程度得分
1.3 多种分类算法结构设计 本文从常用的分类算法模型中挑选了在同一样本集中不同类别的分类正确率差异较大的3 种算法进行涨跌分类,即SVM 模型、Xgboost模型和BP 神经网络模型。SVM 分类算法是一种寻找怎样划分超平面可以使得样本划分的间隔最大的方法,本文使用高斯核函数对两类样本进行软间隔分类,惩罚系数C 为1.0。
Xgboost 算法采用一种类似贪婪的算法构建每一棵决策树,当构建一颗决策树的时候,首先需要满足新树构造后会使整个模型的熵在当前状态下最低,然后还要满足用户设定的阈值才能构建,而每棵树的叶子节点是该节点所对应的分数,模型的输出结果是所有叶子节点的得分值之和。本文使用1.2 中筛选出的8 个特征因子作为模型的输入,其他参数采用交叉验证法,调整至最优状态。
BP 神经网络模型是通过一种有监督的学习方式,训练样本通过输入层进入网络,与网络中的权值进行运算,通过激活函数进入下一层,直到通过最后一层的激活函数,此时的输出才是网络的结果。考虑到输入特征维度为8,需将样本分为2 类,且样本数据不到两百条,所以在网络结构和输出层神经元数量的选择上,本文进行了多次尝试。最后确定网络为单隐层结构,其输入层为8 个神经元,隐层为10 个神经元,输出层为2 个神经元,并引入动量因子对网络的反向传播过程进行优化。首先向输入层输入8 维的特征向量,与隐层的权值矩阵相乘通过sigmoid 激活函数得到隐层的输出值,再与输出层的权值矩阵相乘通过sigmoid 激活函数得到2 个输出,此时输出层的误差为E_output,隐层误差为E_hidden。
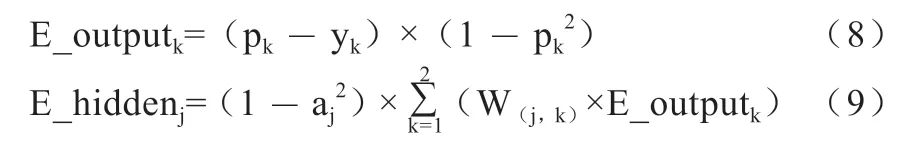
其中,pk为输出层第k 个神经元的输出值,aj为隐层第j 个神经元的输出值,W(j,k)为隐层第j 个神经元对应第k 个输出层神经元的权值。更新网络权值时,按照0.1的学习率α和0.01 的动量系数β更新各层权值。
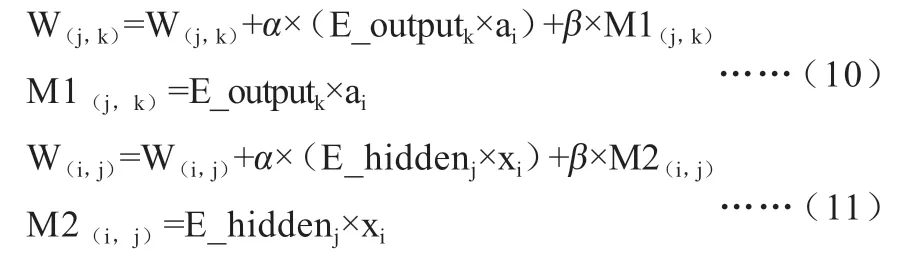
其中,W(i,j)为输入层第i 个神经元对应第j 个隐层神经元的权值,M1 和M2 的初值为全零矩阵,在权值更新时按照(10)和(11)同步更新。模型通过反复训练,最终确定下来的权值参数可以使得下次输入样本时能得到较高的准确率。本文最终使用的网络结构如图3 所示。
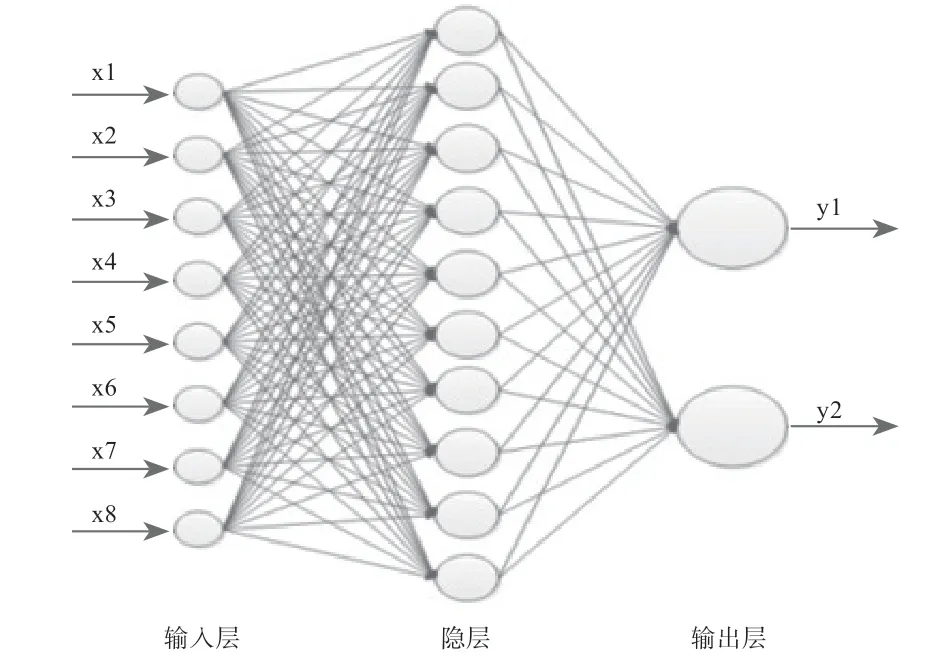
图3 神经网络结构
经多次实验发现,在输入值一致的前提下,各算法模型分类成涨时的正确率与分类成跌时的正确率并不一致。于是本文提出了对2 个算法是涨跌分类正确率最高的那一类结果进行融合的模型组合方式。本文将单模型在涨和跌上的分类正确率作为实验对照组,分别使用BPNN_SVM、BPNN_Xgboost 和Xgboost_SVM 3 种组合进行涨跌分类,2 种模型进行组合时先假设算法A 分类为跌的正确率大于分类为涨时的正确率,且综合正确率大于算法B。如果算法B 分类为涨的正确率大于分类为跌的正确率,则组合后的分类结果为当算法B 分类为涨时该样本为涨,其他样本的结果与算法A 的分类结果一致;若算法B 分类为跌的正确率大于分类为涨时的正确率,则组合后的分类结果仅在2 个算法同时分类为涨时才为涨,其中任意一个算法分类为跌都是跌。
1.4 模型评价标准及实验参数 本文将数据集分成训练集和测试集2 个部分,其中训练集为122 条数据,测试集为37 条数据。本文对使用相同输入的BP 神经网络模型和SVM 模型以及Xgboost 模型进行比较,再将其两两组合,选出综合分类正确率最高的模型,并根据分类结果使用不同参数的多元回归模型预测每月的价格。通过实验摸索,最终确定以每月的月初价格、月末价格、最小值、最大值和月平均价格作为回归模型的自变量,设计了回归模型。再将先分类涨跌再进行预测的方法和不分类直接预测的方法进行对比实验,以平均绝对百分比误差(MAPE)作为模型的评价标准。
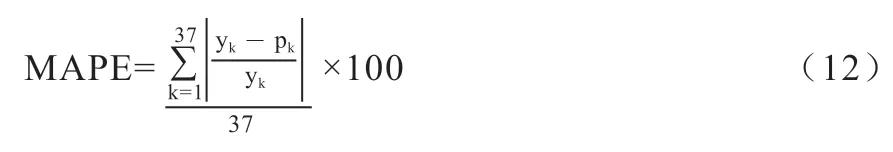
2 结果与分析
2.1 相同参数下各分类模型对比 由表1 可知,BP 神经网络和Xgboost 模型分类为跌的正确率相对较高,但是综合正确率仍然只有90%左右。按照1.3 中两两组合的方式对各算法模型进行结合,结果如表2 所示,使用BP_Xgboost 算法的模型分类正确率不仅高于其余2 组,而且较单一模型而言,准确度也有提升。本文将各模型分类的具体值逐个比较后发现,虽然BPNN 和Xgboost单模型分类成跌的正确率已经很高,但这只能说明模型分类为跌时的可信度更高,但仍然存在跌样本预测成涨的情况。采用以上组合模式,本质上是使用BPNN 的结果对Xgboost 进行优化。还可以将这种组合模式推广到任意两种算法的组合上。假设现有两种算法,其中算法A 的综合正确率大于算法B,如果考虑存在一种极端情况,即算法B 预测为涨的正确率是100%,但综合正确率只有90%。意味着当算法B 预测结果为涨,则该样本一定为涨,但存在涨样本被预测成跌的情况,所以综合正确率仅为90%。那么,从理论上讲,在算法A的预测结果中,用算法B 预测为涨的结果覆盖原算法A的结果。即可达到将算法A 中可能将涨样本预测为跌的情况纠正过来,从而达到提高预测正确率的效果。
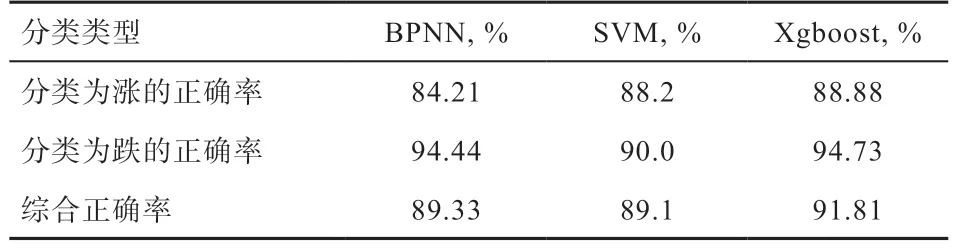
表1 各算法在不同分类上的正确率
2.2 先分类再预测与直接预测的方法对比 图4 展示了2 种方法对生猪价格的预测效果。2 种方法的预测值在数值上虽然只有细微的差别,但从图5 中发现,先分类再预测的MAPE 比直接预测的MAPE 要低,而且图中大部分节点的预测误差都优于直接分类的结果。

表2 各类算法两两组合的分类正确率
2.3 2019 年生猪全国参考价预测 本文从行情宝(http://hqb.nxin.com)上获取了2019 年1 月—2019 年12 月的全国生猪参考价格的日度数据,整理后得到11 个样本。由于数据量太小,且大部分是上涨数据,于是本文将整理后的样本作为测试数据,输入2.2 中的上涨模型中。直接使用上涨模型的回归参数,得到了2019 年2 月—2019 年12 月的预测值,与真实值的对比结果如图6 所示。在除去4 个月价格上涨幅度超过15%的异常情况后,模型预测得到的MAPE 为2.37%。模型的预测误差在3%以内,说明模型可以适应当前的市场环境,可用于一般情况的价格预测,在一定程度上能指导企业的生产活动。
3 结 论
本文提出了一种基于分类模型的生猪价格预测方法。在样本分类阶段,本文使用的BP 神经网络模型和Xgboost 模型两者都在分类为跌样本时有较高正确率,将两者进行组合后整体的正确率提高,说明通过融合2个模型分类正确率最高的那一类的结果,可以提高组合模型的分类正确率。先分类再预测方法得到的MAPE为2.64%,而直接预测方法的MAPE 为2.90%,说明先将样本进行涨跌分类,再对其进行预测,可以降低预测的误差。从2019 年的预测结果来看,除去大幅上涨的异常情况,MAPE 在3%以内,说明本文所使用的方法可以适应当前的市场环境。
但是生猪预测仍然存在一些问题,即预测误差较大的节点往往是生猪价格发生转折的附近。一般来说,价格预测在拐点处的误差会相对较高,因为价格惯性会让模型误以为保持上次预测的趋势,从而造成相反的结果,因此未来研究方向是如何确定价格序列中的拐点,进一步降低误差。
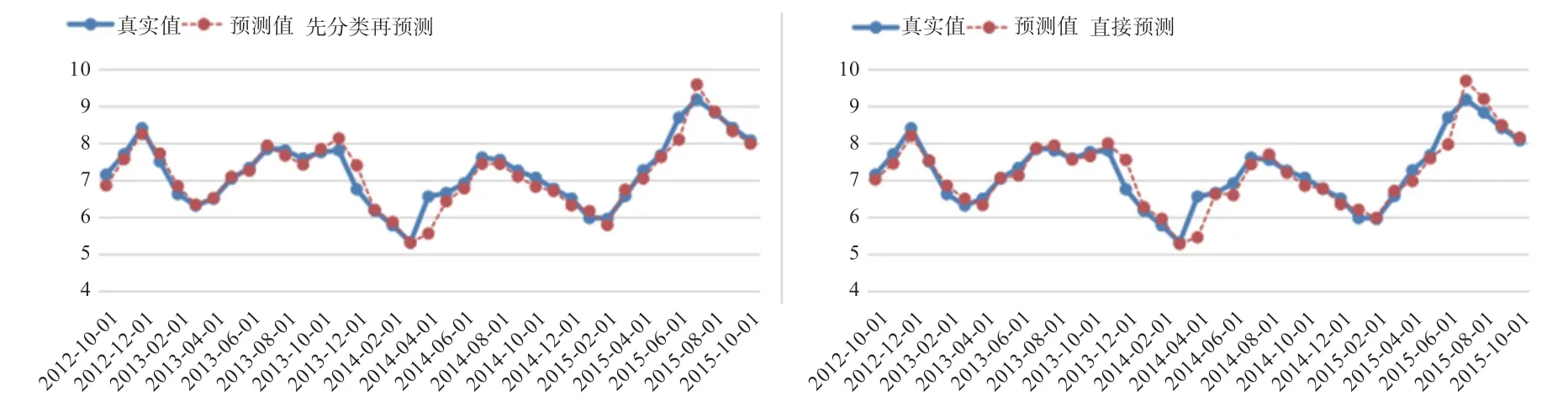
图5 2 种预测方式的MAPE 比较
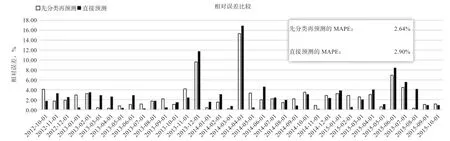
图6 全国生猪价格预测

