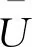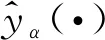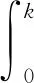半线性微分方程的近似可控性

李建利，陈丽珍

(1.太原学院 应用数学系，山西 太原 030032；2.山西财经大学 应用数学学院，山西 太原 030006)

0 引言

本文主要研究下列微分方程:

(1)

温和解的近似可控性.算子A在Banach空间Y上生成强连续半群T(s)，u(·)是L2(J,U)中给定的控制函数，B是U→Y的有界线性算子，g:J×Y→Y.y0是Y的一个给定的元素，C(J,Y)表示定义在J上取值于Y的连续函数全体，赋予范数‖y‖=sup{|y(s)|:s∈J}.

由于可控性问题与极点配置、结构分解、最优控制等有密切的联系，所以可控性问题在控制理论和工程中占有重要的地位[1,2].近年来，各种微分和脉冲微分系统的可控性问题已被许多人使用不同的方法进行了广泛研究[3-5].在文献[3,4,7]中有半群紧性的假设，也有相应线性系统的可控性假设， 但在无限维的情况下，这些假设是相互矛盾的[6,7].实际上，在这种情况下，可控性仅在子空间上成立.因此，微分方程的近似可控性的研究具有重要意义.在本文中，利用不动点方法和非紧性测度来研究半线性微分方程的近似可控性.

1 预备知识

本节主要介绍一些基本定义、符号及引理.

设yk(y0,u)为系统(1)在终点k对应控制函数u的状态值，y0为初始值.定义集合:

R(k,y0)={yk(y0,u)(0):u(·)∈L2(J,U)}，

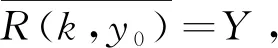
定义算子

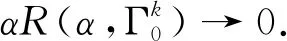
根据文献[8]可知，(S1)成立，当且仅当线性系统

(2)

在J上是近似可控的.

定义1.2若函数y∈C([0,k],Y)满足

则称函数y为问题(1)的一个温和解.

设X为Banach空间，定义X上的Hausdorff非紧性测度MNC，

χ(Ω)=inf{ε>0:Ω在X中有一个有限的ε-网}.

在下面的引理中给出了Hausdorff非紧性测度χ的的一些基本性质.

引理1.3[9]设X为实Banach空间，B1,B2⊆X有界，则满足下列性质：

(ⅰ)B1是预紧的，当且仅当χ(B1)=0；

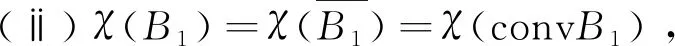
(ⅲ)若B1⊆B2，则χ(B1)≤χ(B2)；

(ⅳ)χ(B1+B2)≤χ(B1)+χ(B2)，其中B1+B2={x+y;x∈B1,y∈B2}；

(ⅴ)对任意的λ∈R，χ(λB1)=|λ|χ(B1).

定义1.4定义有界线性算子G:L1([0,k],Y)→C([0,k],Y)为:

(3)

称之为Cauchy算子，其中T(s)是由A生成的C0半群.

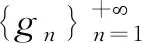
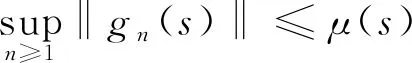
那么对于所有的s∈[0,k]，有

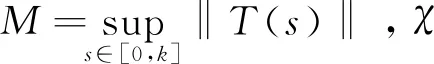
引理1.6[11]假设A:D(A)→Y是Banach空间Y中一致有界线性算子{T(s),s≥0}紧半群的无穷小生成元,那么由:

给出的p>1的算子Q:Lp(J,Y)→C(J,Y)是强连续的.

下面的不动点定理在主要结果的证明中起着关键作用.

y≠λF(y)，

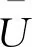
下面仅需证明，对所有α>0，都存在一个连续函数y(·)∈C(J,Y)，使得:

其中:

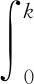
则系统(1)是近似可控的.

2 主要结果

假设：

(H1) 半群T(s)(s>0)，是紧的.

(H2)g:[0,k]×Y→Y；对于几乎处处的s∈[0,k]，函数g(s,·):Y→Y是连续的；对于所有y∈Y，函数g(·,y):[0,k]→Y是可测的.

(H3) 对于所有y∈Y和s∈[0,k]，存在一个函数m∈L1([0,k],R+)和一个非递减连续函数Ω:R+→R+，使得

‖g(s,y)‖≤m(s)Ω(‖y‖).

(H4) 存在一个函数b∈L1([0,k],R+),使得对每个有界集D⊂Y，有

χ(g(s,D))≤b(s)χ(D)，a.e.s∈[0,k]，

其中χ是Hausdorff MNC.

为了方便起见，引入两个符号

定理2.1设Y为实Banach空间.若假设(H1)-(H4)成立，则对于所有的0<α≤1，只要存在一个常数N>0，且满足

(4)

和

(5)

则系统(1)在J上有一个温和解.

证明 对于α>0，将C(J,Y)上的算子Γα定义为

Γα(y)=z，

其中:

下证，对所有α>0，Γα:C(J,Y)→C(J,Y)都有一个不动点.

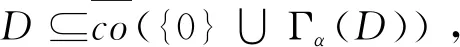
那么对于所有的ε′>ε，存在一个有限族{η1,η2,…,ηj}⊂L2([0,k],U)，使得对于任意的un∈L2([0,k],U)，存在

‖un-ηi‖L2(J,U)≤ε′,i∈{1,2,…,j}.

根据上面的不等式，有:

和

因为

由引理1.3

因此，

利用(5)式，上式表明χ(D)=0.

第3步，设λ∈(0,1)，y=λΓα(y)，那么对于s∈[0,k]，有

因此

所以

那么由(4)可知，存在N使得‖y‖≠N.定义集合

U={y∈C([0,k],Y):‖y‖

定理2.2假设线性系统(2)在J上近似可控，如果满足条件(H1)-(H4)，则系统(1)是近似可控的.

下的一个温和解，且满足等式

Qgα→Qg.

因此，当α→0+时，

其中:

那么当α→0+时，

因此，系统(1)在J上是近似可控的.