关于“ 学生决策能力培养”的理性思考

鄢晓钦

【编者按】近段时间，随着深度学习的理念逐步为广大一线教师所接受，学生高阶思维发展的重要性愈加凸显。高阶思维，意指发生在较高认知水平层次上的心智活动或认知能力。教师在小学数学教学实践中，如何设计能够促发学生创新能力、决策能力与批判性思维等高阶思维能力的情境与活动？本期话题一起来探讨。

当今世界，信息化、智能化、数字化高度融合并快速发展，新时代迫切需求具有高阶思维的人才，同时高阶思维也是学生成长和发展必备的一种思维品质。决策能力是高阶思维能力中的一项重要的能力，它对高阶思维的发展起着至关重要的作用。“决策”是指决定战略或策略，是一个复杂的思维操作过程，是人们面对各种事件通过信息收集、加工，最后做出判断、得出结论的过程。从心理学的角度来看，人在做出决策的过程中，是思维和行动相融合的过程。能力是完成一项目标或者任务所体现出来的综合素质，因此，决策能力是个体或群体在对事件做出决策的过程中所呈现的综合能力。具体来说，决策能力是指人们面对问题时，能够依据已有知识和经验提出多种解决方案，并运用科学方法和科学手段选择出最佳方案的能力。它包括发现与认识问题的能力、信息收集与整合的能力、形成并优化方案的能力。笔者经过长期的调研，发现小学数学教学中对学生决策能力培养的意识是比较淡薄的。因此，本文围绕“学生决策能力培养”作如下阐述。

一、发现与认识问题是做出决策的基础

形成决策的目的是为了更好地解决问题，因此，问题是什么就显得尤为重要，因为它是形成决策的基础。问题从浅层面来看是指要求回答或解答的题目，但能成为决策依据的问题一定是错综复杂的，需要从众多问题中发现关键问题，解决这个关键问题的过程就是决策形成的过程，这就需要学生先发现并认识问题。

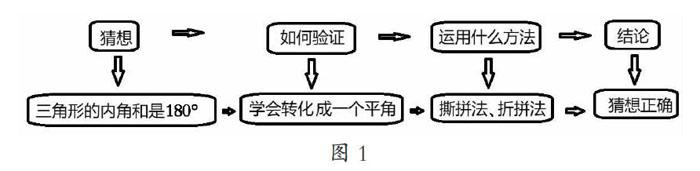
“发现”在《辞海》里是这样解释的：经过研究、探索等，看到或找到前人没有看到的事物或规律。因此，发现的事物或规律是本来就存在的，不是个体创造出来的，但根据个体的经验、感觉、思维等能力的不同，对事物发现的深度和广度也不尽相同。由此分析，“发现问题”指的就是一定主体为了实现一定的目标，根据已有的经验、知识、能力，按照一定的认识方法，在一定条件下根据感觉和思维认识世界事物的现象、本质、规律之间的矛盾。认识问题，指的是在发现问题的基础上，对各个问题形成清晰的认知，做出正确的分析，并在众多问题中找出关键问题，为做出正确的决策提供研究的方向。如何培养学生发现并认识问题的能力？最佳的方式是进行问题式教学，让学生直面需要解决的问题，就能找出背后隐藏的起关键作用的问题。如人教版四年级下册“三角形的内角和”一课要探究的问题是：三角形的内角和是多少度？这是一个浅表性的数学问题，是所有学生都能发现的数学问题，要培养学生形成最后解决问题的决策能力，就要直面该问题进行教学。学生通过用量角器测量，发现三角形内角和大约是180°，由于受到测量方法和工具精确性的影响，有可能造成误差，于是学生提出一个大胆的猜想：三角形的内角和是180°。教学的关键问题是如何验证这个猜想的正确性，在验证的过程中学生就会形成如下的思考过程（图1）。

经历这样的直面问题教学，运用“猜想、验证、结论”三步骤教学，学生的思路有指向性，明确问题的关键点在哪里，懂得运用什么方法解决问题。发现解决问题背后的关键在于如何验证，运用转化的方法把三角形的三个角通过撕拼或折拼的方法组成一个平角，这就实现了问题的转化，三角形内角和的问题也就迎刃而解了。

二、收集与整合信息是做出决策的条件

提出要解决的关键问题，紧接着就是为解决这个问题去收集并整合有用的相关信息，这是形成决策的条件。在收集信息的过程中，明确信息、认识信息、理解信息是做出决策的基础。首先从要解决的问题出发，明确要收集哪些方面的信息，细化收集的任务单，帮助学生收集到全面、有用的信息。其次，要分工合作收集整合信息。一项任务的完成是要小组成员之间既分工又合作，分工是为了减轻学生的任务负担，将收集和整合信息的任务分配给组内的成员，也避免了得到信息的重复性，增强了收集整合信息的实效性。而且，每个成员都带着自己的任务参加，也激发了学生的积极性，在分工合作的学习过程中，很好地培养了学生的合作能力和团队精神，这也是对学生成长过程中必备的核心素养的培养。最后，根据收集的信息做出整合。在整合信息的过程中需要考虑的因素众多，主要思考：从显性信息中能寻找到隐性的关键信息是什么？运用它们能解决哪些相关的问题？这就需要对收集的信息进行例举、分析、研究，挖掘到关键的深层次的信息，从而让信息为决策的形成提供一个强有力的依据。

如人教版五年级上册第一单元例8“解决问题”一课，从题目中可以收集到3个层面的信息。

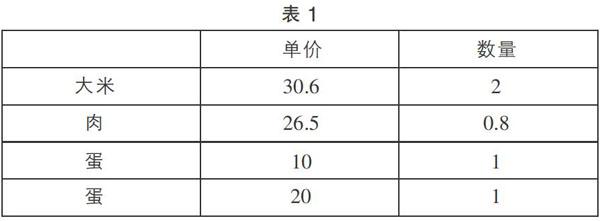
第一层面的信息（表1）。收集到这些信息，可以通过精确的计算来解决问题：100-30.6×2-26.5×0.8=17.6（元），20>17.6>10。因此够买一盒10元的鸡蛋，不够买一盒20元的鸡蛋。

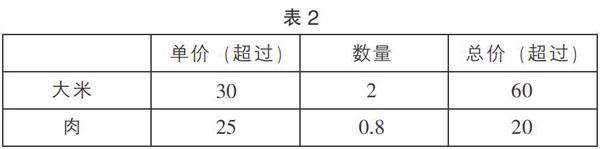
第二层面的信息（表2）。运用估算的方法，把数据往小了估，1袋米超过30元，两袋米就超过60元，1千克肉超过25元，0.8千克肉就超過20元，买米和买肉的钱超过80元，不够买一盒20元的鸡蛋。

第三层面的信息（表3）。依据原始数据，运用估算的方法，把数往大了估，又得出新的信息，算出买大米、肉、蛋的总价与100元的关系如下：62+27+10<100，62+27+20>100。因此够买一盒10元的鸡蛋，不够买一盒20元的鸡蛋。

从问题出发，收集到三个层面的信息，第一个层面是显性的信息，第二、第三两个层面的信息是通过第一层面信息推导出来的，运用它们分别可以解决相关的数学问题。信息的不同决定解决问题的方式是不同的，第一个层面的信息，需要对数据进行准确计算，得出精确数据，再进行比较得出结论。第二层面的信息，是将原信息的数据往小了估形成新的数据，通过计算很容易得出再买一盒20元的鸡蛋，钱是不够的。但较之第一层面的信息，它的应用使问题解决显得便捷。第三层面的信息跟第二层面的信息比较，同样是用估算的方法，但它能很容易得出两个问题的答案——够买一盒10元的鸡蛋，不够买一盒20元的鸡蛋。因此，通过信息的分析与整合，第三层面的信息能最便捷、全面地解决问题，于是，第三层面的信息就成了优选的信息。

三、形成与优化方案是做出决策的核心

方案指的是进行工作的具体计划或对某一问题制订的规划。它是从解决问题出发，确立解决目标，细化操作要求，选用适当的方法，周密部署，形成可操作的计划。决策亦是决定的意思，方案形成后付之行动的实施过程就是决策的过程。因此，方案的形成是做出决策的核心。决策的形成是要经历一系列的过程：确定决策目标—拟订方案—对比方案—分析方案—选取方案—实施方案。决策形成的过程就是对学生决策能力培养的过程，让学生能够根据收集到的信息形成多种解决方案的能力，需要学生的整体规划能力。

但在数学学习中，学生要知道某些问题往往没有明确答案或唯一的解决办法，需要找出多种替代方案并在决策时给予考虑。而且在解决问题的过程中，思考的方向、方法等因素不同，就会形成不同的方案。为了让决策更有实效性，需要对方案进行对比、优化，从而做出最后的判断。同时，优化方案的运用也能很好地落实优化思想在学习中的运用，让学生理解对待解决方案要好中选优、择优而用。

优化决策要遵循以下几个原则：①从结果来看，选取的决策确定能解决问题。②从过程来看，要能快速便捷地解决问题，提高解决问题的效率。③从方法来看，要能促进学生的思考，提高学生数学思考的能力。

如人教版四年级下册第一单元例5“租船问题”一课：经过学生的合作探究學习，会得出多种方案。方案①：假设全部租小船，（32÷4）×24=192（元）。方案②：假设全部租大船，32÷6=5（条）……2（人），（5+1）×30=180（元）。对比两种方案，发现第二种方案比第一种来得优惠，引导学生探寻原因，发现是坐大船每个人的单价比较低，由此选取第二种方案，尽量坐大船。接着引导学生再次思考，还有更优惠的租船方案吗？在学生互动学习、互相启发中得出了第三种方案。方案③：假设租5条大船，1条小船：30×5+24=174（元）。随着学习和思考的深入，发现小船上依然空着两个座位，这还不是最优惠的方案，只有座位不空着且都坐满人才是最优惠的租船方案。方案④：假设租大船4条、小船2条，30×4+24×2=168（元）。

整个学习的过程先后形成四种租船方案，运用了“先假设，后调整”的探究学习方式，引导学生从四个方案中明辨优劣，根据最优惠租船这个目标，得出最优惠的租船方案，避免了决策的偏颇。在决策方案对比中，对各种方案的优劣进行对比，做出评价，算出结果，培养了学生全面看待问题、全局思考、对比分析、择优选择的学习能力。经历这样的学习过程，也就让学生拥有了形成并优化方案的能力，促进了决策的形成，很好地培养了学生的决策能力。

（作者单位：福建省福州市钱塘小学教育集团湖前校区）

微言

教师与学生，成人与儿童在思维领域的差异以及矛盾，造成数学思维交流与沟通的阻隔。因此，非常有必要寻找到适合小学生思维层次的指导方法，晓之以理，启迪思维，引领学生数学思维的深度发展。

——福建省连江县第二实验小学 蔡诗莺