求解正则化非负低秩逼近问题的交替最小二乘算法

黄琼慧， 段雪峰

(桂林电子科技大学 数学与计算科学学院，广西 桂林 541004)

考虑下述非负矩阵的正则化低秩逼近问题。

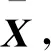
在信息时代，结构化矩阵的低秩逼近频繁出现在金融工程[1]、图像与信号处理[2]、潜在语义分析[3]及机器学习[4]等学科与领域。Park等[5]提出了Hankel矩阵低秩逼近的总体最小范数算法，随后此算法被应用于Sylvester矩阵的低秩逼近计算。与上述算法相比，Cadzow算法[6]对于求解结构矩阵低秩逼近问题更加简单便捷。基于牛顿法和交替最小二乘算法，Schost等[7]提出类牛顿迭代算法求解结构低秩逼近问题，且该迭代算法能够局部收敛于一个低秩结构矩阵。Duan等[8-9]基于Gramian representation和特殊三角函数变换将相关矩阵的低秩逼近问题转化为无约束优化问题，并构造共轭梯度算法进行求解。随后，他提出非单调谱投影梯度法求解Q范数下的相关矩阵低秩逼近问题。Chu等[10]系统地研究了结构低秩逼近问题及其在信号处理和蛋白质折叠等方面的应用。

求解问题1的关键在于如何刻画问题中的可行集

鉴于此，利用矩阵的满秩分解处理可行集中的秩约束，基于交替最小二乘法求解等价的非负矩阵分解问题，提出投影梯度法求解相关子问题并证明其收敛性，并用数值例子验证方法的可行性。

1 主要结果

1.1 交替最小二乘法

引理1n×n阶矩阵X的秩小于等于r，当且仅当存在矩阵W∈Rn×r,H∈Rr×n，使得X=WH。

由引理1，问题1的可行集可刻画为如下形式：

Ω={X=WH|W≥0,H≥0,W∈Rn×r,

H∈Rr×n}。

因此问题1可等价转化成问题2。

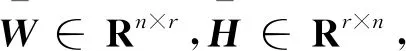
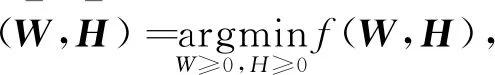
其中，

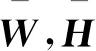
应用如下交替最小二乘算法求解问题2。

算法11)初始化W1≥0,H1≥0。

2)当k=1,2,…时

(1)

(2)

该算法也称作有界约束优化中的块坐标下降算法[11]，即其中一个向量块对应的目标函数在相应的约束条件下被最小化，而其余的块是固定的。该算法处理的是最简单的情况，即只有W、H两个块向量。

由文献[12]中的推论2，有如下收敛性结果。

定理1算法1所产生序列{Wk,Hk}的任意收敛点为问题2的稳定点。

实现算法1的关键在于求解式(1)和(2)，其中式(1)和(2)都为有界约束优化问题，故设计投影梯度方法进行求解。

1.2 投影梯度法

考虑下列有界约束优化问题的标准形式：

其中：f(x):Rn→R为连续可微函数，l和u分别为上界和下界。则投影梯度方法的迭代规则为

xk+1=P[xk-αkf(xk)]，

其中，

的作用是将点映射至有界可行域中。

利用Armijo线搜索下的投影梯度法求解上述有界约束优化问题。

算法21)给定0<β<1，0<σ<1，初始化任意可行点x1。

2)当k=1,2,…时，

xk+1=P[xk-αkf(xk)]。

其中：αk=βtk，且tk为满足不等式

f(xk+1)-f(xk)≤σf(xk)T(xk+1-xk)

的最小非负整数t。

关于式(2)，可将其重写为

s.t.Hij≥0,∀i,j。

(3)

其中，A、B、C、W为常数矩阵。

根据Shepherd的描述[13]，式(1)和(2)应用投影梯度法的更新规则为

Wk+1=max(0,Wk-αkWf(Wk,Hk)),

Hk+1=max(0,Hk-αkHf(Wk,Hk))，

其中αk为步长。因此，求解式(2)的投影梯度算法如下。

2)计算投影梯度

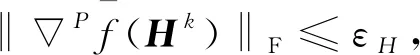
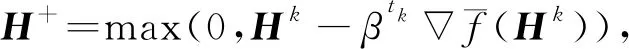
的最小非负整数t，令

将式(1)重写为与式(3)同样形式：

s.t.Wij≥0,∀i,j，

其中H为常数矩阵，则可应用与算法3类似的算法获得式(1)的解Wk+1。

2 数值实验

利用数值例子验证交替最小二乘算法求解问题2的可行性。实验在MATLAB 2016a环境下运行。

在数值实验中，设(Wk,Hk)处的投影梯度为Pf(Wk,Hk)，其中(Wk,Hk)为算法1中第k次迭代值，停机标准为‖Pf(Wk,Hk)‖F≤ε‖f(W1,H1)‖F。

例1给定矩阵

设α=0.3，r=2，初始值：

用算法1求解，经13次迭代得到问题2的最优解：

从而问题1的最优解为

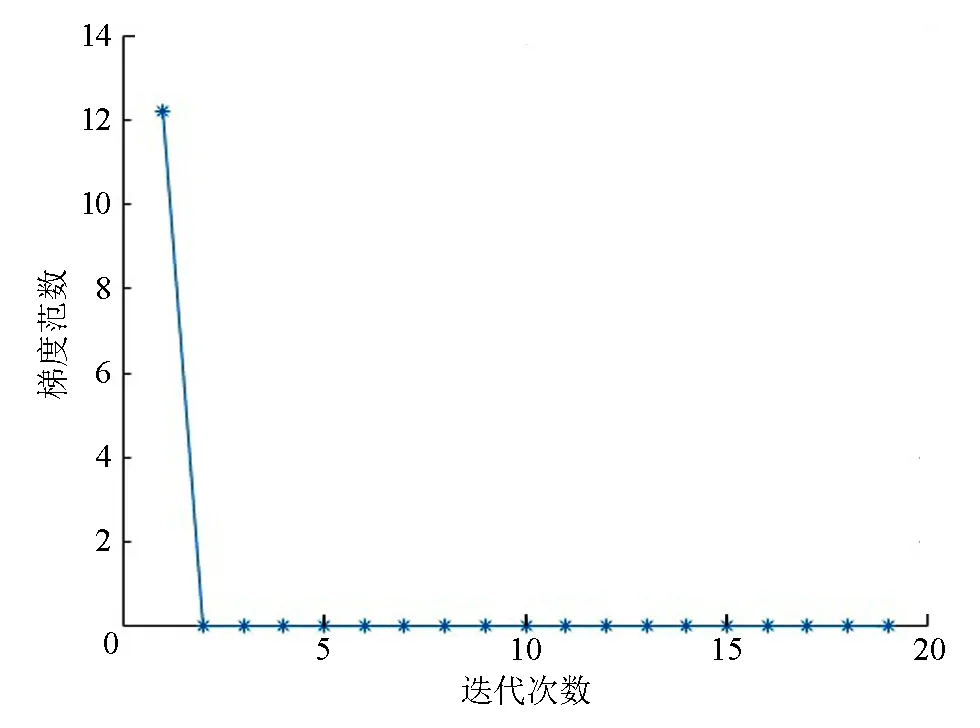
图1 n=3，r=2时的梯度范数曲线

例2给定矩阵：

A=

B=

C=

设α=0.3，r=3，初始值：

H0=

用算法1求解，经26次迭代得到问题2的最优解：

从而问题1的最优解为

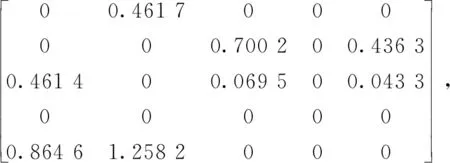
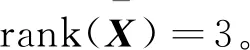
图2 n=5，r=3时的梯度范数曲线

3 结束语

利用矩阵的满秩分解及其相关性质,将非负矩阵的正则化低秩逼近问题转化为等价的非负矩阵分解问题，并利用交替最小二乘方法求解非负矩阵分解问题，用投影梯度法求解相关的子问题。数值实验表明，此方法是可行的。