修正的共轭梯度法在压缩感知中的应用
马金瑶,朱志斌,杨子琳
(桂林电子科技大学 数学与计算科学学院,广西 桂林 541004)
压缩感知理论由Donoho、Candes和华裔科学家Tao等提出,相比于传统的奈奎斯特理论,需要采样的频率高于信号最高频率的2倍以上,压缩感知理论在低于传统采样率条件下获取采样信号,并恢复稀疏信号,提高采样效率,节省了成本。基于此,压缩感知理论利用信号的稀疏性,广泛用于信号的恢复问题。
压缩感知理论不仅在科学研究,如低秩恢复、抽样理论、统计学习等中应用,而且在工程领域也有广泛应用,如核磁共振成像、地震成像、雷达等。最近更是在无线通讯系统中获得了学者们的大量关注。
1 稀疏信号恢复
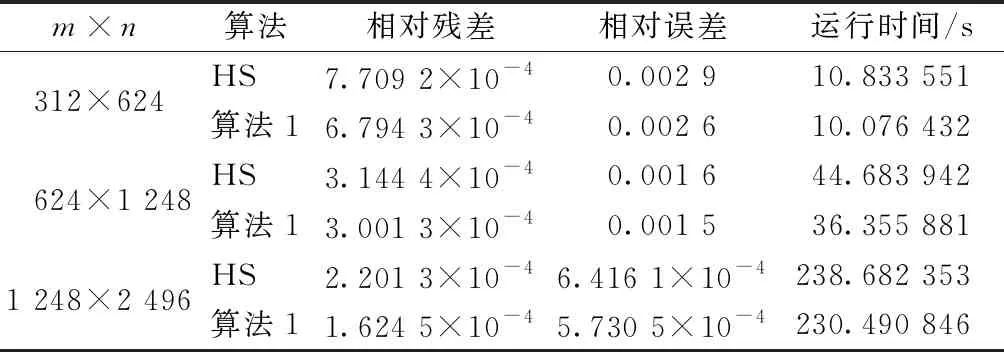
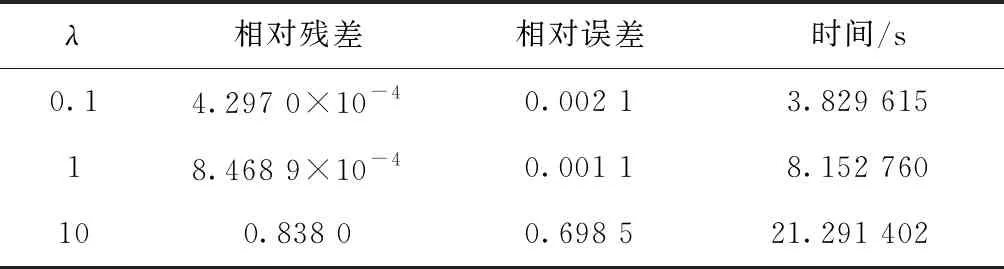
利用压缩感知恢复信号,本质是从Ax=y重建恢复稀疏信号x∈CN(其中测量矩阵A∈Cm×N,测量向量y∈Cm,m min‖x‖0, s.t.Ax=y。 (1) 然而,问题(1)是一个NP难问题,因此转化成一个与问题(1)有相同解的l1范数问题[2]: min‖x‖1, s.t.Ax=y。 (2) 已知l1范数问题是约束凸优化问题,求解这个问题可转化成求解基追踪去噪最小化问题[3]: (3) 因为‖x‖1是非光滑的,先将‖x‖1进行光滑化处理[4], (4) 此时, minF(x)。 (5) 其中F(x)的梯度为 F(x)=λfτ(x)+AT(Ax-b)。 共轭梯度法是求解无约束凸优化问题的有效方法之一,标准迭代格式为[5] xk+1=xk+αkdk, (6) (7) 其中:gk=F(xk),dk为搜索方向;αk为利用某种线搜索获得的步长;βk为共轭梯度法中的一个参数。4种βk计算公式为: 确定了4种经典的共轭梯度法,分别称为PRP法、FR法、DY法和HS法。近年来,许多学者对βk进行了改进。基于拟牛顿法,Dai和Liao[6]得出如下新的βk公式: (8) (9) 文献[7]对HS和LS进行了如下改进: 文献[8]采用新的迭代格式 (10) 其中: yk-1=gk-gk-1=F(xk)-F(xk-1)。 在以上迭代格式的前提下,提出新的修正的共轭梯度法, (11) (12) 该算法的具体步骤为: 1)任取初始点x1∈Rn,参数0<δ<σ<1,ε>0,τ0=0.6,d1=-g1,k=1; 2)若‖gk‖≤ε,且τk≤ε,则停止,否则转步骤3; 3)由Wolfe线搜索准则[9]求得步长αk,即αk满足 (13) (14) -‖gk‖2<0, 所以结论成立。 为了分析算法的收敛性,给出以下假设: 假设1水平集μ={x∈Rn:F(x)≤F(x1)}有界,即存在一个常数B>0,使得 ‖x‖≤B,∀x∈μ。 假设2在水平集μ的一个邻域N内,F连续可微,梯度函数满足Lipschitz连续,即存在常数L>0,使对任意的x,y∈N,有 ‖g(x)-g(y)‖≤L‖x-y‖。 证明由引理1及假设1知,{F(xk)}为单调下降有界序列,故{F(xk)}为收敛数列。又由假设2和式(14)得 故有 又由式(13),得 所以结论成立。 定理1设假设1和2成立,则算法或有限步终止于gk=0,或产生无穷点列{xk},使得 在本试验中,算法参数为t1=0.8,t2=0.3,ε=10-4,终止条件为‖gk‖≤ε或迭代次数超过2 000。 为了检验本算法的实际数值效果,用经典的HS共轭梯度算法[10]和算法1进行数值比较实验,利用Matlab编程。表1在正则化参数等于0.1的前提下,给出了在不同维数的测量矩阵下2种算法的对比实验结果;表2在测量矩阵A的维数都是312×624的前提下,正则化参数λ选取为0.1、1、10时,分别给出算法1的数值结果;图1是测量矩阵A的维数为312×624,分别取λ为0.1、1、10,应用修正的算法1进行信号恢复的效果图,其中圆圈为原始信号,圆点为恢复出来的信号。 表1 2种算法的对比结果 图1 λ取不同值时算法1的恢复效果图 表2 λ取值不同时算法1的数值结果 将提出的新的共轭梯度法应用到利用压缩感知解决信号恢复的问题。在一定的测量矩阵维数下,选取不同的正则化参数进行了实验。在相同条件下,与经典的HS共轭梯度法进行了对比实验。实验结果表明,利用提出的共轭梯度法解决信号恢复问题是可行的。
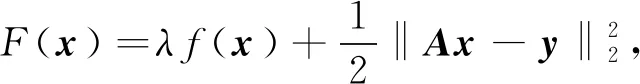
2 修正的共轭梯度法
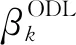


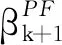
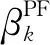
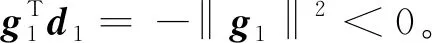

3 全局收敛性

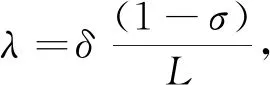


4 数值实验

5 结束语

