道岔区固定辙叉心轨垂磨对轮轨动态接触的影响
杨新文,张 昭,孟 玮,钱鼎玮,胡耀华
(1.同济大学轨道交通结构耐久与系统安全上海市重点实验室,上海,201804;2.同济大学道路与交通工程教育部重点实验室,上海201804)
道岔是铁路轨道结构的薄弱环节之一,在既有普速铁路线开行重载货车会导致道岔结构变形加剧,从而影响重载货车过岔的安全性和平稳性[1-2]。由于道岔区固定辙叉存在有害空间,心轨垂直磨耗超限现象普遍,直接影响列车过岔辙叉区轮载过渡,而在普速铁路中,固定型辙叉道岔占大多数,且《普速铁路线路修理规则》中明确将固定辙叉心轨垂直磨耗作为养护修理的一项控制标准[3]。心轨垂直磨耗是指辙叉区心轨轨顶面垂向磨耗,心轨垂直磨耗会造成心轨与翼轨顶面高差增大,是影响道岔辙叉区轮轨动力性能的重要因素,直接影响过岔时轮轨接触在翼轨与心轨之间的过渡,从而造成轮载过渡时产生较大的冲击力,从而加剧钢轨伤损,甚至影响行车安全性与平稳性。因此,探明辙叉区心轨垂直磨耗对重载车辆通过固定辙叉的轮轨接触影响规律有非常重要的意义。
关于列车过岔时辙叉区轮轨接触关系,国内外学者们进行了诸多研究。文献[4]通过建立车辆与轨道动力学混合预测模型,研究分析了列车通过辙叉的车轮冲击荷载和噪声。Shupp 等[5]利用多体动力学软件Simpack 分析了列车通过固定式辙叉单开道岔时的轮轨多点接触问题以及车辆的动力学性能。翟婉明[6]采用垂向冲击函数模型模拟了列车通过固定型辙叉的轮轨垂向冲击响应。司道林和杨东升等[7]建立了高速道岔辙叉动力学模型,分析了高速列车通过辙叉区时的动力学响应,提出通过设置合理的翼轨抬高值可以改善辙叉区结构不平顺的动力效应。徐井芒等[8]在分析固定辙叉伤损规律的基础上,提出了基于车轮踏面高差值的固定辙叉优化设计方法。李文博等[9]通过优化设计辙叉关键断面位置处心轨降低值、翼轨加高值等措施来降低辙叉区的轮轨垂向相互作用,从而提高车辆通过道岔时的安全性和平稳性。李跃鹏等[10]根据新型重载道岔平面线型及结构尺寸,对嵌入式高锰钢辙叉和合金钢辙叉两种型式进行了研究,提出了适应于朔黄铁路的新型重载道岔的强化措施。曹洋、王平等[11]基于车轮踏面在翼轨和心轨间过渡时的轮轨接触几何关系和动力相互作用,提出了心轨关键断面降低值的选取及评价方法,并用该方法对心轨降低值进行了优化。
本文通过对道岔辙叉区钢轨廓形进行实测分析,研究道岔固定辙叉区心轨垂直磨耗的分布规律。针对重载条件下60 kg·m-1钢轨12 号固定辙叉单开道岔,基于车辆-道岔耦合动力学的理论建立重载货车-道岔动力仿真模型,计算分析了重载货车各方向过岔时,心轨垂直磨耗对重载列车过岔辙叉区轮载过渡范围轮轨接触的影响,可为重载化普速道岔养护维修提供技术支持。
1 道岔区心轨垂直磨耗的分布规律
1.1 现场实测
以既有普速铁路60 kg·m-1钢轨12 号单开道岔为研究对象进行多次抽样测试,测试时选取道岔为既有客货混运线路固定辙叉提速道岔,该类型道岔是典型的重载化普速道岔。钢轨廓形测试采用非接触式轮廓测量仪CLIPRI C4X 进行测量,该测量仪通过激光束测量出钢轨廓形,速度快、精度高、误差小。现场测试情况如图1所示。

图1 测试道岔和测试仪器Fig.1 Measuring turnout and instrument
测试范围包括道岔轮载过渡区在内的辙叉心轨-翼轨变截面区域,由于道岔部分截面旁有联结部件(如:限位器、顶铁等)阻碍激光廓形测试,测点间距略有偏差,后续进行了拟合处理。测试廓形位置以辙叉理论尖端为原点,沿逆向过岔方向依次测试,在辙叉区共测试7 个典型廓形,分别距理论尖端距离为-1.470、-0.760、0、0.155、0.635、1.355 和1.625 m。选出有代表性的几个辙叉区钢轨断面测试廓形,距离辙叉理论尖端距离以顺向过岔为正,逆向过岔为负,如图2所示。图中,y和z分别表示钢轨横向和纵向坐标。
1.2 心轨垂磨分布规律
12号单开固定辙叉道岔采用的是高锰钢整铸辙叉,根据辙叉标准图纸,各心轨轨顶宽截面参数如表1 所示,将测得的辙叉廓形数据进行分析处理后,将其与标准数据进行对比,并考虑了心轨轨顶宽度,如图3 所示。图3 中横虚线为辙叉心宽40 mm 断面位置,竖虚线为辙叉心宽40 mm 处对应钢轨断面距理论尖端的距离。
由图3 可知,在心轨顶宽20~40 mm 范围是实测心轨垂磨较大的区域,成因是轮载从翼轨过渡到心轨时,存在有害空间,造成了很大的冲击荷载,根据文献[1],正常状态下道岔高锰钢整铸辙叉叉心顶宽20~35 mm 处为轮载过渡段,而轮载过渡段心轨轨头宽度较窄,结构薄弱,易发生磨耗等伤损。图3中横虚线为以辙叉心宽40 mm断面处垂磨为基准。
1.3 拟合心轨垂磨
根据《铁路线路修理规则》[3],高锰钢整铸辙叉损伤标准以辙叉心宽40 mm 断面处(图3 中横虚线所示)垂磨为基准,规范中对不同线路心轨磨耗伤损值有着较为详细的界定,但对于重载化普速道岔情况下仍需具体分析。车轮反复冲击碾压后,受道岔结构、车辆轴重、速度等诸多因素影响,心轨垂磨的分布随机性较大,难以拟合出符合各种实际情况下的心轨垂磨分布曲线。本文根据实测心轨垂磨分布规律进行简化拟合:以心轨顶宽40 mm处为基准,根据距心轨顶宽73 mm断面的距离线性拟合出心轨顶宽 40 mm 处垂磨为 3、4、5 和 6 mm 时的各关键截面心轨-翼轨高差表和心轨-翼轨顶面高差空间曲线,拟合心轨垂磨的各级分布曲线与实际心轨垂磨分布的共性规律存在一定的相似性,具有工程参考价值,如图4 所示。将标准的7 个辙叉区关键截面的心轨顶部曲线向下平移对应的偏差值得到对应的心轨与翼轨顶面高差截面,下面列举心轨顶宽30、40 和50 mm截面各级心轨垂磨廓形,如图5所示。
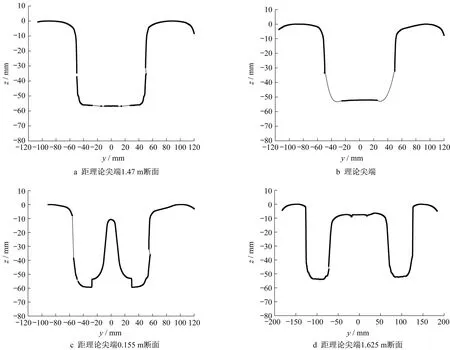
图2 实测辙叉廓形Fig.2 Measured profile of frog

表1 整铸辙叉截面参数Tab.1 Section parameters of cast manganese-steel frog
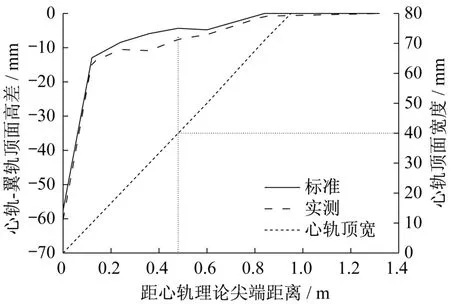
图3 实测心轨-翼轨高差与标准值对比Fig.3 Comparison of the difference between measured nose rail-wing rail height and standard value
2 车辆-道岔耦合动力学模型
为了研究心轨垂磨对重载列车过岔辙叉区轮载过渡范围轮轨接触的影响,建立重载货车-道岔动力仿真模型,其中道岔为60 kg·m-1钢轨12号固定辙叉单开道岔,计算分析了重载货车各方向过岔时车辆和轨道耦合动力响应。

图4 拟合心轨各级垂磨曲线Fig.4 Fitting curve of vertical wear of nose rail at each level
2.1 车辆模型
本文建立了包含2个转K6型转向架的C80重载货车,转K6 型转向架属于“三大件”式转向架,采用两系悬挂。1个转K6型转向架主要由2个侧架、1个摇枕和2个轮对组成,车体、侧架和轮对均设置为完整的5个自由度,摇枕仅考虑沉浮和摇头运动的2个自由度,整车模型共有49个自由度。重载货车轴重25 t,固定轴距1.83 m,车轮滚动圆半径0.42 m,车辆定距8.7 m,一系悬挂纵向、横向和垂向刚度分别为13、11和160 MN·m-1,二系悬挂纵向、横向和垂向刚度分别为4.4、4.4和4.89 MN·m-1。
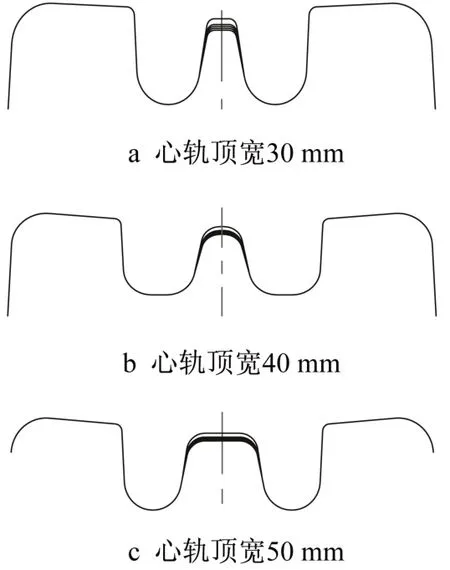
图5 各心轨垂磨下辙叉关键截面Fig.5 Typical profile of frog under each level of nose rail vertical wear
2.2 道岔模型
(1)道岔钢轨变截面处理
对于钢轨变截面特性处理方式主要是通过预先给定一系列关键截面,随后通过插值计算出整条渐变的钢轨截面。标准图纸给出了道岔变截面钢轨转辙区的7个控制截面和辙叉区的8个控制截面,根据这些标准截面通过线性插值可得到其间任一截面的廓形,如图6和图7所示。

图6 尖轨-基本轨的关键截面Fig.6 Key sections of switch rail-stock rail
(2)12号单开道岔平面线型
12 号单开道岔平面布置图如图8 所示,图中各变量含义说明列于表2。
(3)道岔动力学模型

图7 心轨-翼轨的关键截面Fig.7 Key sections of frog nose rail-wing rail
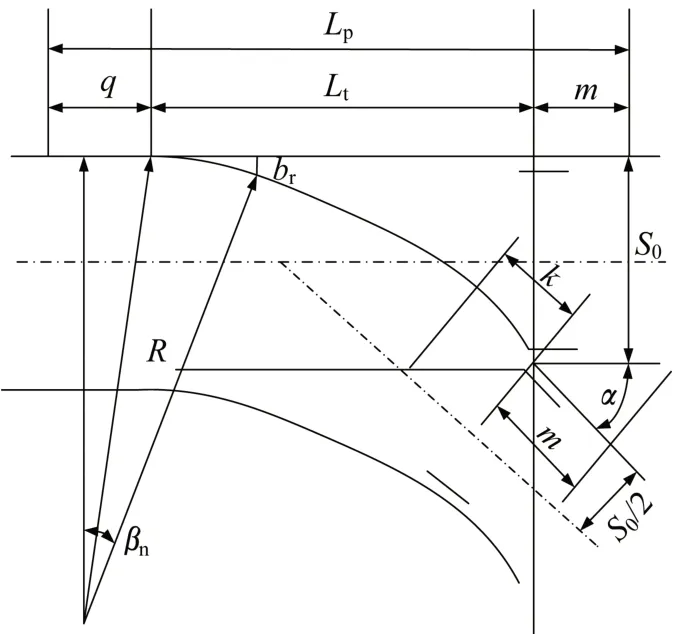
图8 道岔平面图Fig.8 Plan view of turnout
在道岔动力学计算中,轨道结构采用弹性轨道建模。钢轨采用欧拉梁模型,考虑了垂向和横向运动;支承条件采用按轨枕间距分布的离散弹性点支承,用线性弹簧-阻尼单元模拟;轨枕采用欧拉梁模型,考虑了垂向和横向运动;枕下垫层采用分布式线性弹簧和阻尼单元进行模拟[6],路基部分由于变形较小,本文不考虑对其影响。如图9所示,Kpz,Cpz分别为轨下垫板垂向刚度与阻尼系数;Ksz,Csz分别为枕下垫层垂向刚度与阻尼系数;Kpy,Cpy分别为钢轨扣件横向刚度与横向阻尼系数;Ksy,Csy分别为枕下垫层横向刚度与阻尼系数。
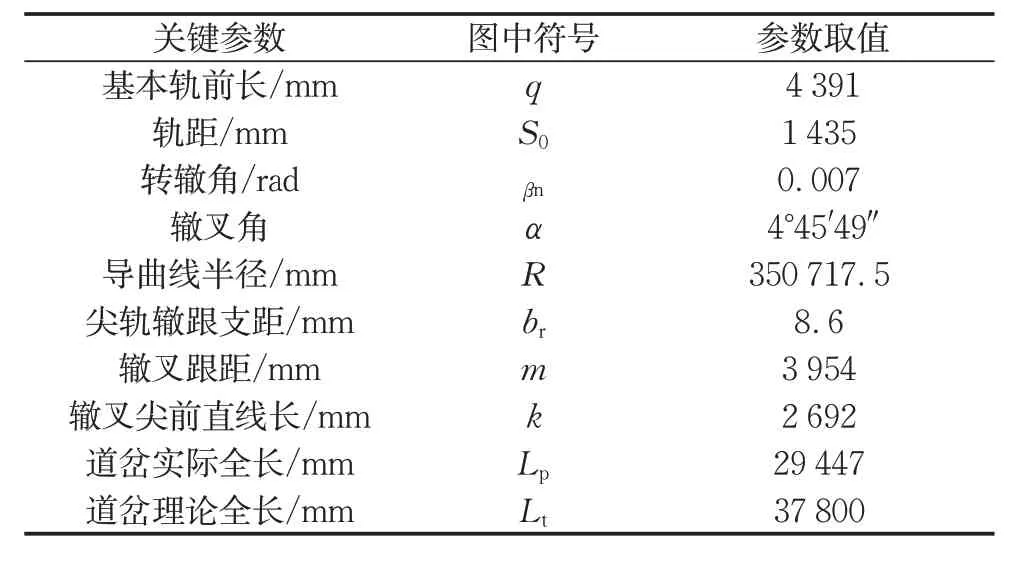
表2 12号单开道岔线形关键参数Tab.2 Key parameters of No.12 single turnout
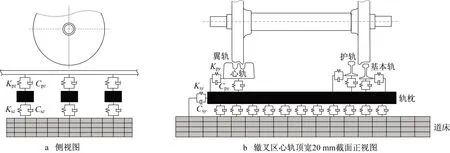
图9 轨道结构动力学模型Fig.9 Track dynamics model
(4)轮轨接触算法
在道岔转辙区的轮轨接触中,轮轨接触点将在尖轨和基本轨之间转移,轮载转移会影响轮轨滚动接触过程中的轮轨相互作用关系,因此采用的轮轨接触计算方法应兼顾精度和效率。本文采用Kik-Piotrowski[12](K-P)多点接触力学模型来进行轮轨接触法向力和切向蠕滑力的计算。
2.3 模型验证
为了验证本文建立的重载车辆-道岔耦合动力学的正确性及结果的可靠性,此处将以本文所建模型的计算结果与国内外相关文献中具有代表性的仿真结果进行对比。文献[13]中仿真分析了25 t轴重货车以45 km·h-1速度侧逆向通过12 号重载道岔的动力学特性,本文在建立了整段道岔模型的基础上,仿真分析了25 t轴重货车以45 km·h-1速度侧逆向通过60 kg·m-1钢轨12号普速道岔的动力学特性,将文献[13]与本文仿真计算结果中的轮轨横向力和轮轨垂向力对比如图10所示。
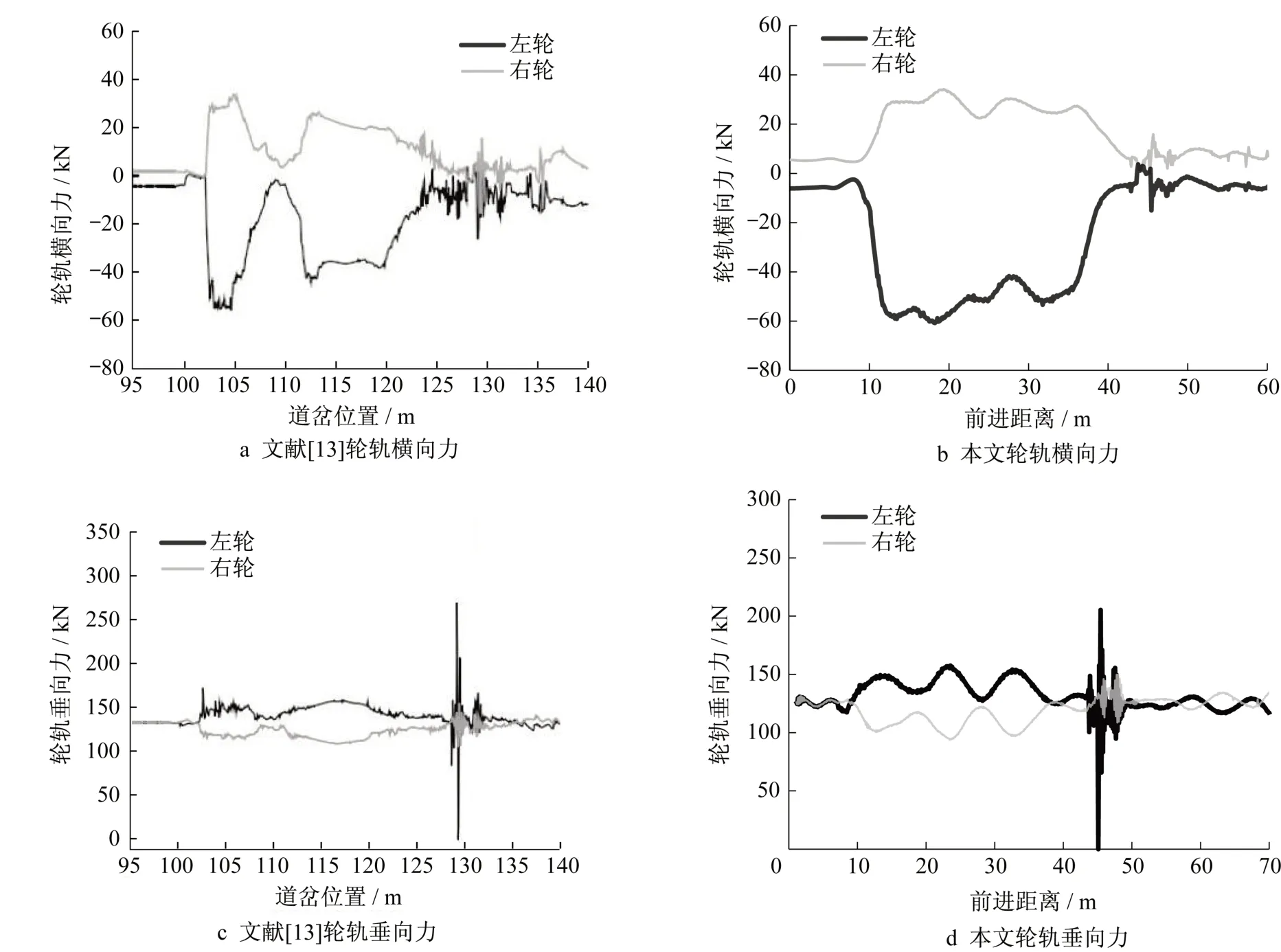
图10 文献[13]与本文仿真计算轮轨力比较Fig.10 Comparison of wheel-rail force in literatureRef.[13]’s and this paper’s simulation calculation in this paper
由图10可知,在车辆进入转辙区后本文与文献[13]中计算得到的轮轨横向力和轮轨垂向力均会产生突增并伴随波动,表明车轮与截面发生变化的基本轨和曲尖轨间的动力作用较为剧烈,在道岔尖轨截面变化结束时,钢轨截面突变为基本轨的标准截面,并且已进入导曲线。因此使得轮轨作用力也相应地减小,道岔导曲线一般未设超高,故该段轮轨横向力大于直线段的对应指标,轮轨垂向力出现一侧大于另一侧的偏载现象。进入辙叉区后,可以看出由于固定辙叉有害空间的存在,轮轨垂向力峰值较大。综上所述。列车侧逆向通过道岔区时,文献[13]仿真计算结果与本文仿真计算轮轨力各峰值大小、时程波形和变化规律较为一致。本文建立的重载车辆-道岔耦合动力学模型可用来进行道岔转辙区相关动力学计算分析。
3 心轨垂磨对辙叉区轮轨接触的影响
以轴重25 t的重载车辆以40 km·h-1的恒定速度侧逆向通过60 kg·m-1钢轨12 号右开道岔辙叉区为例,轨顶面摩擦系数取0.35,轨距角摩擦系数取0.15,计算分析了心轨垂磨量对轮轨接触点位置和接触力的影响。图11 是重载车辆以40 km·h-1的速度侧逆向过岔时轮轨接触点在转辙区和辙叉区的过渡轨迹,其中,垂直于接触斑平面的接触力N1为轮轨接触法向力,平行于接触斑平面且在于钢轨截面廓形平面内的接触力F1为轮轨接触横向蠕滑力,N2为轮缘接触点处轮轨接触法向力,F2为轮缘接触点处切向力,β1为N1与竖向坐标轴的夹角,β2为N2与竖向坐标轴的夹角,如图12所示。

图11 轮载过渡轨迹Fig.11 Distribution of rail load transition

图12 轮轨接触力示意图Fig.12 Wheel-rail contact force
图13 为心轨顶宽40 mm处垂磨为5 mm时重载车辆第1位轮对轮载过渡侧轮轨接触点在钢轨表面和车轮廓形上的轨迹,根据接触点位置,远离轮缘为第1接触点,靠近轮缘为第2接触点。
由图13 可知,辙叉区轮载过渡区非常短,以轮轨冲击的方式完成轮载过渡。随着心轨垂直磨耗增大,车轮与心轨碰撞点远离理论尖端。轮轨碰撞点沿钢轨纵向后移远离理论尖端,而对横向位置影响较小。图14 和图15 为侧逆向过岔辙叉区第1 位轮对轮载过渡侧接触法向力和横向蠕滑力在翼轨和心轨的转移情况。
由图14 和图15 可知,当心轨不发生磨耗时,轮载在心轨和基本轨转移时较为平稳,轮轨冲击较小,但随着垂磨的增大,轮载过渡前后接触力波动增大,接触力峰值增大,轮载过渡不再稳定。进一步,在直向过岔速度为70 km·h-1,侧向为 40 km·h-1的工况下,将车辆不同过岔方向的辙叉区第1 位轮对的轮载过渡撞击点位置进行统计整理,如表3所示。
由表3可知,当心轨顶宽40 mm截面垂磨量从0增至6 mm时,轮载过渡碰撞点逐渐远离理论尖端并造成“有害空间”的增大。以侧逆向过岔为例,轮轨碰撞点从距离理论尖端289.20 mm 远离至379.07 mm,相隔89.87 mm。为定量研究心轨垂磨量对辙叉区轮轨动力作用的影响,将各心轨垂磨量下重载车辆以不同方向通过既有普速道岔的轮轨垂向力和轮重减载率进行对比分析(图16)。
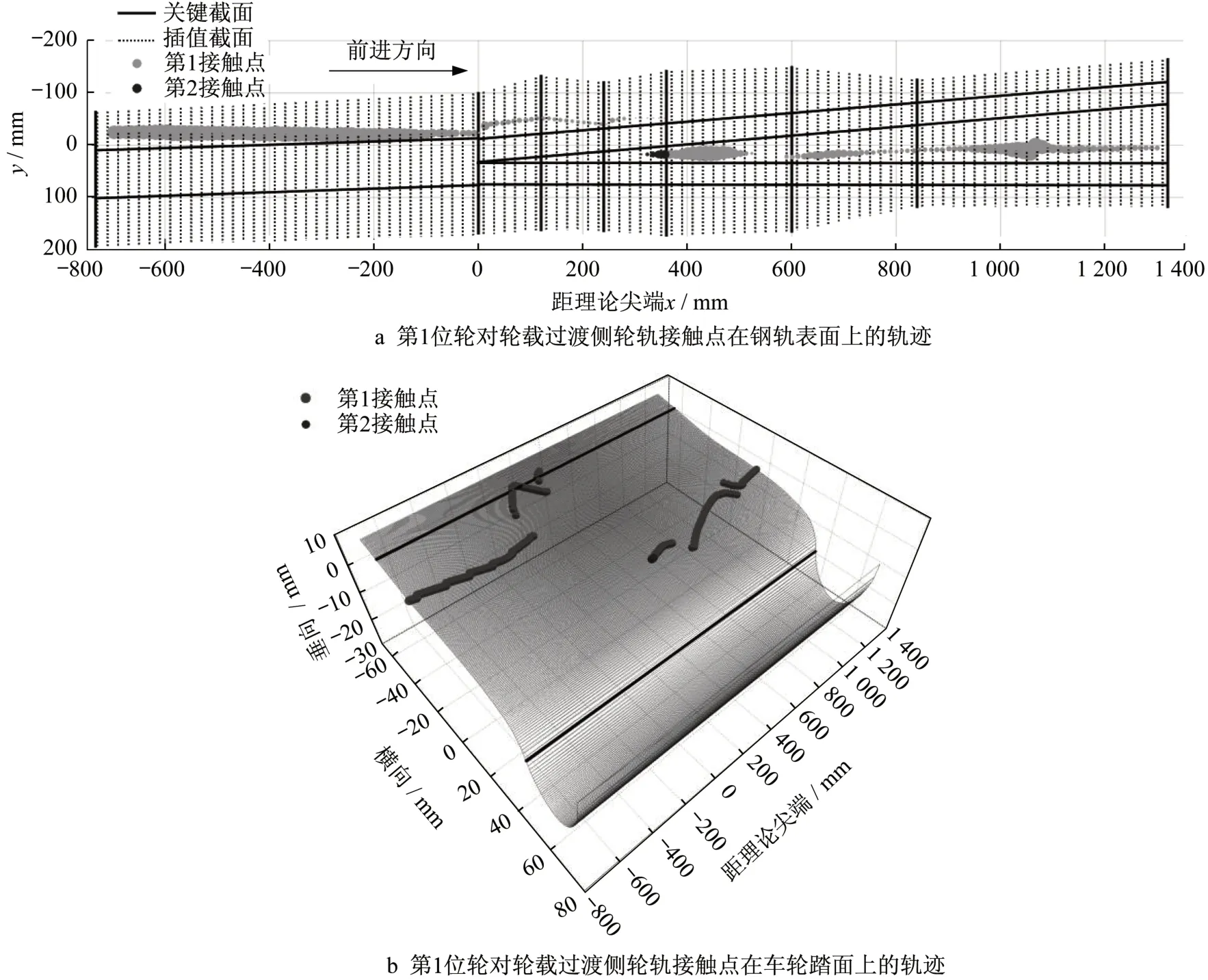
图13 心轨垂磨量对辙叉接触点轨迹的影响Fig.13 Effect of vertical wear of every nose rail on wheel-rail contact point
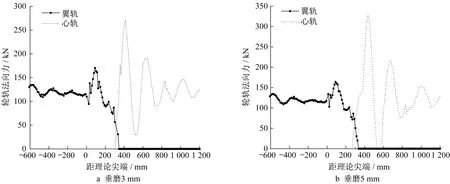
图14 辙叉区轮载过渡接触法向力Fig.14 Wheel-rail contact normal force when rail load transition in frog nose rail
由图16 可知,当心轨顶宽40 mm 截面垂磨从0增大到6 mm 时,轮轨垂向力方面,直向过岔大于侧向过岔。以直逆向过岔为例,辙叉区垂向力最大值从213.917 kN增大到295.621 kN;当心轨垂磨达到6 mm 时,轮轨垂向力已超出限值250 kN,轮重减载率已超出第一限值0.65。由此可得,辙叉区各动力学指标最大值均会随着心轨垂磨偏差增大而增大,根据动力学指标超限情况,综合考虑辙叉区轮轨接触点位置,当轨道几何不平顺较为良好时,心轨顶宽40 mm处垂磨应控制在5 mm之内。
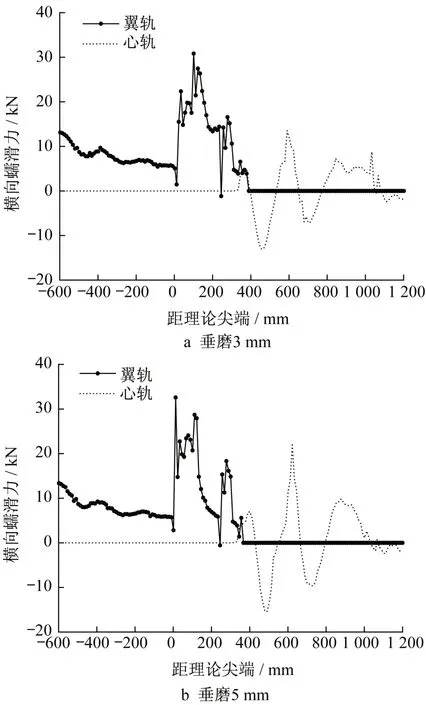
图15 辙叉区轮载过渡接触横向蠕滑力Fig.15 Wheel-rail lateral creep force when rail load transition in frog nose rail
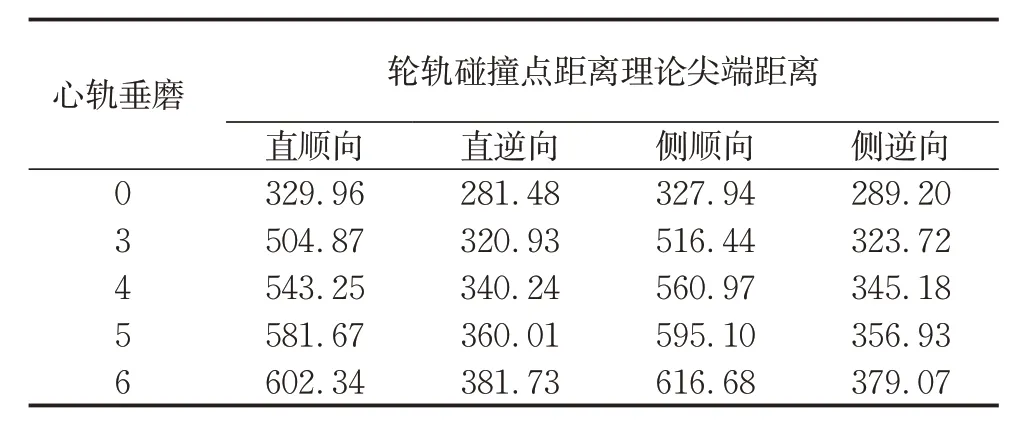
表3 心轨垂磨对辙叉区轮载过渡撞击点位置的影响Tab.3 Influence of nose rail vertical wear on the impact point location when rail load transition in frog mm
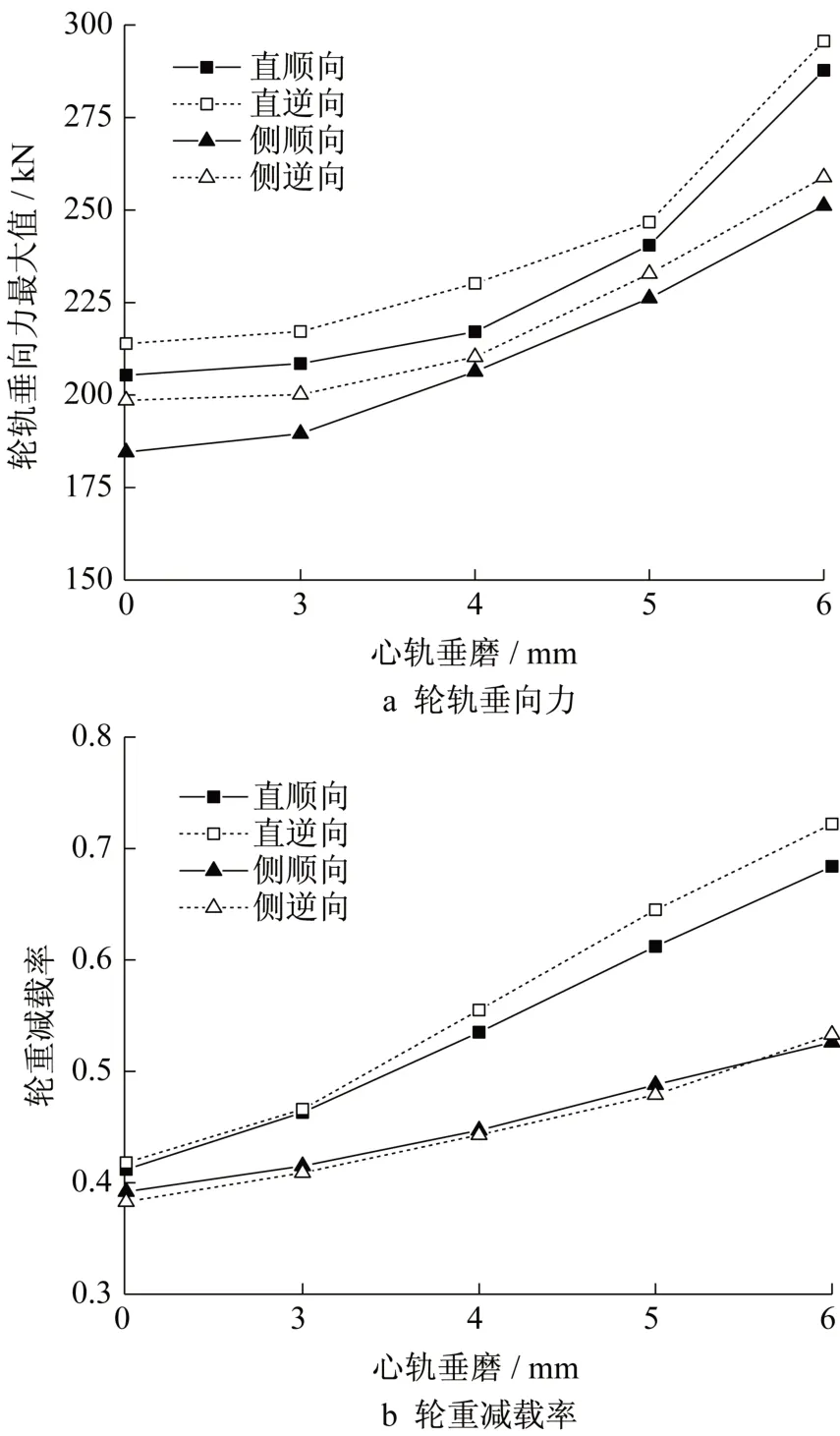
图16 心轨垂磨对辙叉区动力学指标最大值影响Fig.16 Influence of nose vertical wear of rail on maximum dynamic index of frog area
4 结论
本文针对重载条件下60 kg·m-1钢轨12 号固定辙叉单开道岔,基于车辆-道岔耦合动力学的理论,建立重载货车-道岔动力仿真模型,计算分析了重载货车不同方向过岔时,心轨垂磨对重载列车过岔辙叉区轮载过渡范围轮轨接触的影响,得出的主要结论如下。
(1)由于固定辙叉存在有害空间,轮载过渡范围内心轨受到车轮荷载冲击作用,心轨顶宽20~40 mm范围是实测心轨垂磨较大的区域。
(2)辙叉区轮载过渡区非常短,以轮轨冲击的方式完成轮载过渡。随着心轨垂磨增大,车轮与心轨碰撞点远离理论尖端,轮载过渡前后接触力波动增大,接触力峰值增大,轮载过渡不再稳定。
(3)当心轨顶宽40 mm 截面垂磨量从0 增至6 mm 时,轮载过渡碰撞点逐渐远离理论尖端并造成“有害空间”的增大,辙叉区轮轨接触法向力最大值随之增大,增速逐渐变快而横向蠕滑力最大值随机性较强,无明显规律。
(4)综合考虑辙叉区轮轨接触点位置,当轨道几何不平顺较为良好时,心轨顶宽40 mm 处垂磨应控制在5 mm之内。
综上所述,心轨垂磨的增大会造成轮载过渡不平稳,从而导致列车过岔行车安全与平稳性下降,过大的轮轨冲击力会进一步恶化辙叉区道岔结构。

