风险感知交叉演变下突发事件网络舆情传播模型研究
苏妍嫄 张亚明 何旭 杜翠翠
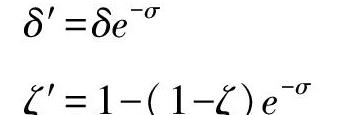
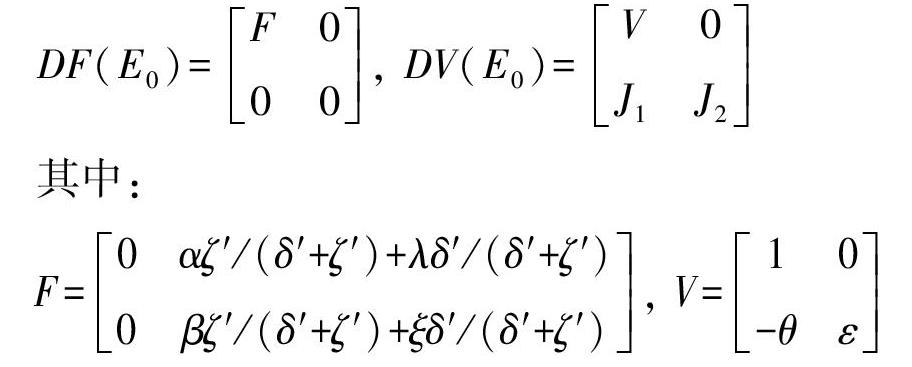
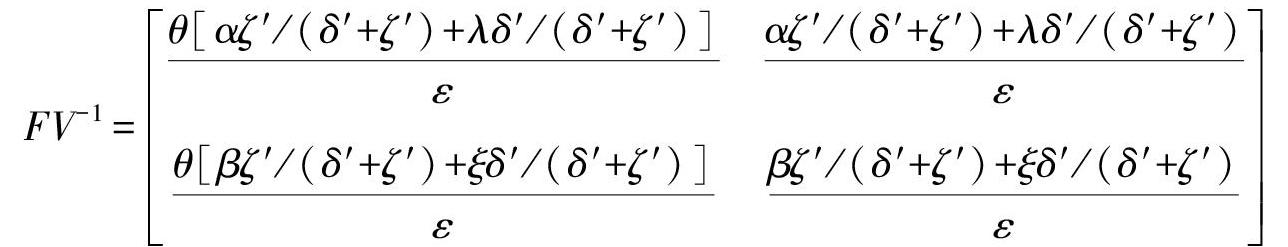
收稿日期:2020-07-11
基金项目:中国博士后科学基金面上资助项目“虚实互动的网络舆情传播模型与负面效应调控算法研究”(项目编号:2019M651067);河北省科学技术研究与发展计划软科学研究项目“面向重大突发公共安全事件的网络舆情传播态势演变与干预研究”(项目编号:19456232D);河北省社会科学发展研究课题“非传统安全事件网络舆情传播模型与干预研究”(项目编号:2019041201001)。
作者简介:苏妍嫄(1991-),女,讲师,博士,研究方向:舆情传播。何旭(1995-),男,硕士,研究方向:信息传播。杜翠翠(1995-),女,硕士,研究方向:舆情治理。
通讯作者:张亚明(1962-),男,教授,博士,博士生导师,互联网+与产业发展研究中心主任,研究方向:复杂网络信息传播。
摘 要:[目的/意义]突发事件网络舆情传播对健全舆情引导机制,推动国家治理体系和治理能力现代化具有重要意义。[方法/过程]借鉴传染病动力学模型,基于公众风险感知异质性与交叉演变性双重视角,通过剖析突发事件驱动的风险感知交叉演变机制,构建了网络舆情传播模型并求解出基本再生数。[结果/结论]“北京新发地疫情”网络舆情实证与仿真结果表明,公众风险感知异质性越小且受突发事件影响越大,网络舆情最终扩散规模及产生的影响越大。突发事件恶化将促使交叉演变向高度风险感知倾斜,加剧网络舆情传播;突发事件好转将促使交叉演变向低度风险感知倾斜,有助于控制网络舆情大规模扩散。政府面对突发事件应立即启动应急响应,降低公众风险感知水平,实现网络舆情有效干预,维护社会和谐稳定。
关键词:突發事件;网络舆情;公众风险感知;传播动力学模型;交叉演变
DOI:10.3969/j.issn.1008-0821.2020.12.011
〔中图分类号〕C912.63 〔文献标识码〕A 〔文章编号〕1008-0821(2020)12-0100-14
Research on Network Public Opinion Propagation Model of
Emergency under Cross-Evolution of Risk Perception
Su Yanyuan1,2 Zhang Yaming1,2* He Xu1 Du Cuicui1
(1.School of Economics and Management,Yanshan University,Qinhuangdao 066004,China;
2.Research Center of Internet Plus and Industry Development,Yanshan University,
Qinhuangdao 066004,China)
Abstract:[Purpose/Significance]It is of great significance to study the network public opinion propagation of emergencies for improving public opinion guiding mechanism and promoting the modernization of national governance system and capacity.[Method/Process]Based on the dynamic model of infectious diseases,and the dual perspectives of heterogeneity and cross-evolution of public risk perception,this paper constructed the network public opinion propagation model by analyzing the cross-evolution mechanism of risk perception driven by emergencies.Besides,the basic reproduction number was also calculated.[Result/Conclusion]The empirical and simulation results of the network public opinion of“Beijing New Epidemic”showed that the smaller the heterogeneity of public risk perception and the greater the effect of emergencies was,the larger the scale and influence of network public opinion propagation were.The deterioration of emergencies would make the cross-evolution incline to the high risk perception,and intensify the spreading of network public opinion.However,the improvement of emergencies would promote the cross-evolution to the low risk perception,and it is helpful to control the scale of network public opinion.The government should start the emergency response immediately to reduce the level of public risk perception,realize the effective intervention of network public opinion,and maintain social harmony and stability.
Key words:emergencies;network public opinion;public risk perception;spreading dynamics model;cross-evolution
近年来,新冠肺炎疫情、无锡高架桥坍塌事故、利奇马台风、7·23甬温动车事故、8·12天津滨海新区爆炸事故等突发事件频繁发生,给人们的生活带来了严重威胁。特别是自媒体时代,伴随移动智能终端普及与在线社交网络井喷式增长以及5G商用,公众可借助各种网络平台实时表达情感、态度、意见、观点,致使突发事件网络舆情瞬间涌现,引爆网络舆论场。尤其是一些无良媒体或个人趁机发布谣言等虚假舆情信息制造噱头,导致网络空间非理性情绪、负面情绪甚至极端情绪泛滥,进一步加剧网络群体集聚。此外,加之公众所处环境、个人经历、知识结构等各不相同,对同一事件具有不同的风险感知水平并交叉演变,使得网络舆情传播更加复杂,致使次生衍生突发事件以及连锁反应爆发风险不断增大,挑战政府的治理与控制能力,引起巨大负面效应,对公共安全、社会和谐稳定甚至国家安全构成了严重威胁。由此可见,网络舆情已经成为突发事件的晴雨表和放大器,结合个体差异性研究风险感知交叉演变影响下的突发事件网络舆情内在传播规律,对健全舆情引导机制、推动国家治理体系和治理能力现代化具有重要意义。
1 文献综述
构建数学模型并进行系统仿真是当前剖析突发事件网络舆情传播机制的主要研究方法。鉴于舆情传播与疾病传播的相似性,传染病动力学模型为研究舆情传播问题提供了基础理论参考。Daley D J等率先将传染病动力学模型应用到谣言等舆情传播中,将个体分为易感者、传播者、免疫者3类,进而构建出经典的D-K模型[1]。随后,一些学者在此基礎上通过进一步细化传播过程对模型进行改进[2-6]。然而,信息技术的飞速发展与在线社交网络井喷增长使得舆情传播模式发生了深刻变革,直接采用经典泛化的传染病模型已不能精准刻画网络舆情几何级数裂变传播过程[7]。其中一个重要原因是疾病传播是无意识的,感染者是否传播疾病不以人的主观意志为转移,但网络舆情传播本质是社会传播,特别是突发事件网络舆情传播过程凝聚着人类行为社会属性[8-11],与疾病传播具有本质差异。因此,还需要进一步结合网络舆情内容属性、公众社会属性等因素进行研究[12-14]。Zhang L等对传播网络舆情的用户状态进行细分,提出了SI3R网络舆情传播模型[15]。尚明生等为有效应对重大非常规突发事件,融合社会网络与传播动力学模型,建立了应急管理集成仿真原型概念框架,提出了以非常规突发事件为情景的仿真规划方法[16]。王家坤等考虑到线上、线下活动的相互依赖性,基于复杂网络理论和传播动力学等方法,构建双层社交网络上的舆情传播模型[17]。赵海峰等以地铁突发事件为例,综合考虑时间有限性与空间有限性,在传统有界信任模型中引入局部沟通和有限理性两个因素,建立了地铁突发事件舆情传播模型[18]。刘小洋等考虑网络动态演变影响,构建了突发公共事件动态网络扩散舆情传播动力学模型[19]。王治莹等分别定义公众类型与政府干预作用,结合突发事件舆情传播特点构建了政府干预下的舆情传播控制模型[20]。种大双等考虑公众状态转移关系和政府干预影响,构建政府干预下舆情传播控制SEIRS模型,运用控制因子实现突发事件网络舆情有效干预[21]。Yin F等针对用户参与讨论一个主题后可能会进入另一个相关主题的行为,提出一种多信息M-SDI重大公共卫生突发事件舆情传播模型,并基于新浪微博新型冠状病毒舆情数据进行分析,以了解突发事件网络舆情传播模式[22]。Wang Z等分析突发事件后多舆情相互促进传播过程,提出了3SI3R模型[23]。
上述研究模型为分析突发事件网络舆情传播规律奠定了重要理论研究基础。然而值得注意的是,这些研究普遍将处在同一状态的个体归为一类而忽略了公众风险感知异质性影响。所谓风险感知是指个体对存在于外界的各种客观风险的感受和认识,并强调是个体由直观判断和主观感受所获得的经验对认知的影响[24]。事实上,由于公众知识结构、所处环境、生活经历等具有差异性[25-27],即便暂时处在同一状态的公众也会具有不同的风险感知水平,进而产生不同的传播倾向。特别是突发事件发生后,面对网络空间涌现的大量舆情信息,绝大部分公众会因信息不对称而凭借个人知识储备、经验阅历做出判断,并根据感知的风险决定是否传播网络舆情进而表现出相应行为。一般而言,距离突发事件发生地越近的公众风险感知水平越高,越倾向传播网络舆情,而距离越远的公众风险感知水平越低,越倾向理性思考后再做决定,且伴随《关于办理利用信息网络实施诽谤等刑事案件适用法律若干问题的解释》《网络信息内容生态治理规定》等系列法律法规出台,公众传播网络舆情越来越谨慎理智。此外,公众风险感知水平还随自身对突发事件相关信息掌握情况以及事态发展变化发生交叉演变。一方面,随着公众对突发事件与自身关联度了解的深入,公众风险感知水平逐渐交叉演变。例如,当起初认为突发事件与自身关联度不大的公众发现亲朋好友处在事件爆发地时,风险感知水平会由低度演变为高度。相反,当起初对突发事件高度恐慌的公众发现自身及家人好友所受影响较小时,风险感知水平会由高度演变为低度;另一方面,突发事件发展变化对公众风险感知水平交叉演变具有驱动影响,公众风险感知水平既可能受外界影响随突发事件激化而逐渐上升,同时也可能随公众对事件可控性的了解以及问题解决而逐渐下降。为此,本文拟基于公众风险感知异质性与演变性双重视角,剖析突发事件驱动的公众风险感知交叉演变机制,构建网络舆情传播动力学模型,通过实证分析与数值仿真验证模型有效性,进一步分析突发事件公众风险感知交叉演变下的网络舆情传播规律。
2 突发事件驱动的公众风险感知交叉演变机制分析
突发事件发生后,公众往往会根据事件可控性、事件对经济社会影响、事件发生在自身可能性以及对自身工作生活的影响等评估并感知风险。由于公众所处环境、个人阅历等存在差异,面对同一突发事件往往产生不同程度的风险感知,进而在收到相关网络舆情时产生不同的传播行为。为简单起见,将公众风险感知水平分为两类,即高度风险感知与低度风险感知。其中,具有高度风险感知的公众通常受突发事件影响较大或对事件极度敏感,如身处突发事件发生地的公众等。这类公众往往受到突发事件刺激处在恐慌、焦虑状态,迫切了解并转发相关舆情信息,甚至对信息真假失去理性判断能力,在收到相关网络舆情后更容易出现盲目传播行为。与之相反,具有低度风险感知的公众一般受突发事件影响较小,或受过专业训练,如远离事发地的公众等。这类公众能够理性看待与应对突发事件,收到相关网络舆情信息后,往往更倾向查阅相关资料或者思考之后再决定是否传播。
一般而言,公众风险感知水平并非一成不变。一方面,随着公众对突发事件的深入了解,公众风险感知水平逐渐发生交叉演变。当公众发现突发事件并非自己想象那样可怕或不可控时,风险感知水平更侧重向低度交叉演变;而当公众意识到突发事件具有严重威胁性、危害性时,风险感知水平更侧重向高度交叉演变。特别地,由于公众所处环境、个人经历等诸多方面具有异质性,某一阶段不同公众风险感知水平演变方向也存在差异,因而存在高低风险感知水平同步演变情境。如地震灾害发生后,当地震级数与烈度不是很大时,距离震中较远或未有震感的公众通常风险感知水平较低,但当这些公众得知亲朋好友恰好在震中或附近工作时,风险感知水平通常会由低度向高度演变,而对于身处外地但家乡在震中附近的公众通常在起初风险感知水平较高,但与家人沟通后发现未受较大影响时风险感知水平会逐渐降低,因此对于同一起突发事件,不同公众在同一时段风险感知水平存在同步交叉演变现象;另一方面,受突发事件事态发展驱动影响,公众风险感知水平同样也会发生交叉演变。若突发事件防控不当,事态朝负向演变并逐渐恶化,则交叉演变中公众风险感知水平逐渐上升;若突发事件得到有效解决,事态朝正向演变且逐渐好转,则交叉演变中公众风险感知水平逐渐下降。
为剖析公众风险感知交叉演变机理,假设伴随公众对突发事件的深入了解,公众由高度风险感知自发演变为低度风险感知的概率为δ,由低度风险感知自发演变为高度风险感知的概率为ζ。受突发事件驱动影响,公众风险感知交叉演变中由高度演变为低度的概率为δ′,由低度演变为高度的概率为ζ′。令突发事件对公众风险感知交叉演变所产生的驱动作用为σ,借鉴文献[28-30],当突发事件防控不当,事态逐渐恶化时,则:
δ′=δe-σ
ζ′=1-(1-ζ)e-σ(1)
当突发事件得到有效解决,事态逐渐好转时,则:
δ′=1-(1-δ)e-δ
ζ′=ζe-σ(2)
两种事态发展情形下,公众风险感知交叉演变概率变化趋势分别如图1、图2所示。
3 突发事件网络舆情传播动力学模型构建
3.1 突发事件网络舆情传播机理分析
根据之前学者的研究及上述分析,网络空间公众类型可以分为5种,即高度风险感知未知者(S1)、低度风险感知未知者(S2)、犹豫者(E)、传播者(I)、免疫者(R)。其中,高度风险感知未知者指尚未听说某网络舆情,但因受到突发事件刺激处在极度恐慌、焦虑状态,收到网络舆情后难以理性判断且易盲目传播的公众。低度风险感知未知者指尚未听说某网络舆情,但收到网络舆情后易倾向理性思考判断的公众。犹豫者表示已经收到网络舆情,但对信息真假持怀疑态度尚未传播的公众。传播者表示正在传播网络舆情的公众。免疫者表示得知网络舆情,但对此没有兴趣或认为网络舆情为虚假信息不进行传播的公众。考虑公众风险感知差异及交叉演变特征,提出如下突发事件网络舆情传播规则,并据此剖析公众风险感知交叉演变下突发事件网络舆情传播机理。
1)当某一高度风险感知未知者S1(i)接收到一位传播者I(j)发送的网络舆情信息后,该高度风险感知未知者S1(i)可能因不确定信息真假以概率α变为犹豫者E(i),也可能迫切分享信息,以概率β变为传播者I(i)将网络舆情传播给他人,还可能认为网络舆情信息与实际情况不符等以概率γ变为免疫者R(i)。根据文献[31-32]状态转移表示方法,可得:
S1(i)+I(j)αE(i)+I(j)
S1(i)+I(j)βI(i)+I(j)
S1(i)+I(j)γR(i)+I(j)(3)
由于高度风险感知未知者S1(i)接收到传播者I(j)发送的网络舆情后一定得知该信息,因而一定发生状态转移,故有α+β+γ=1。
2)当某一低度风险感知未知者S2(i)接收到一位传播者I(j)发送的网络舆情信息后,该低度风险感知未知者S2(i)可能对此持怀疑态度以概率λ变为犹豫者E(i),也可能信以为真,以概率ξ变为传播者I(i)将网络舆情传播给他人,还可能对此毫无兴趣以概率η变为免疫者R(i)。同上,该低度风险感知未知者S2(i)的状态转移过程可表示为:
S2(i)+I(j)λE(i)+I(j)
S2(i)+I(j)ξI(i)+I(j)
S2(i)+I(j)ηR(i)+I(j)(4)
由于低度风险感知未知者S2(i)接收到传播者I(j)发送的网络舆情后一定得知该信息,因而一定发生状态转移,故有λ+ξ+η=1。
3)当某一公众为犹豫者E(i)时,该犹豫者E(i)经过查阅资料论证后,可能觉得网络舆情信息有一定道理以概率θ变为传播者I(i),也可能经过理性思考后判定网络舆情为虚假信息或认为传播网络舆情没有实际意义,以概率(1-θ)变为免疫者R(i)。该犹豫者E(i)的状态转移过程可表示为:
E(i)θI(i)
E(i)1-θR(i)(5)
4)当某一传播者I(i)将网络舆情传播给他人后,该传播者I(i)可能因精力有限,随着时间推移以概率ε停止传播网络舆情变为免疫者R(i),則该传播者I(i)的状态转移过程可表示为:
I(i)εR(i)(6)
5)随着公众对突发事件的进一步了解以及突发事件的发展变化,未知者的风险感知水平也不断发生交叉演变。假设i为高度风险感知未知者S1(i),j为低度风险感知未知者S2(j),在突发事件驱动影响下,高度风险感知未知者S1(i)以概率δ′转变为低度风险感知未知者S2(i),低度风险感知未知者S2(j)以概率ζ′转变为高度风险感知未知者S1(j)。
S1(i)δ′S2(i)
S2(j)ζ′S1(j)(7)
3.2 突发事件驱动的S1S2EIR网络舆情传播动力学模型
根据上述分析,分别用S1(t)、S2(t)、E(t)、I(t)和R(t)表示t时刻高度风险感知未知者S1、低度风险感知未知者S2、犹豫者E、传播者I、免疫者R的密度。这里忽略网络空间人数变化,则有S1(t)+S2(t)+E(t)+I(t)+R(t)=1。根据上述传播规则,公众各状态转移概率可分别写为:
pS1→E=αI(t)
pS1→I=βI(t)
pS1→R=γI(t)
pS2→E=λI(t)
pS2→I=ξI(t)
pS2→R=ηI(t)
pS1→S2=δ′
pS2→S1=ζ′
pE→I=θ
pE→R=1-θ
pI→R=ε(8)
其中,概率α、β、γ、λ、ξ、η、θ、ε、δ、ζ均位于[0,1]之间,突发事件对公众风险感知交叉演变所产生的驱动作用σ为非负常数。根据上述分析,突发事件公众风险感知交叉演变下网络舆情传播过程可用图3表示。
综上所述,可构建如下突发事件网络舆情S1S2EIR传播动力学模型:
dS1(t)dt=-S1(t)I(t)-δ′S1(t)+ζ′S2(t)
dS2(t)dt=-S2(t)I(t)-ζ′S2(t)+δ′S1(t)
dE(t)dt=αS1(t)I(t)+λS2(t)I(t)-E(t)
dI(t)dt=βS1(t)I(t)+ξS2(t)I(t)+θE(t)-εI(t)
dR(t)dt=γS1(t)I(t)+ηS2(t)I(t)+(1-θ)E(t)+εI(t)(9)
3.3 S1S2EIR模型基本再生数分析
在网络舆情传播分析中,基本再生数R0是衡量网络舆情能否大规模扩散的重要参数,表示无干预情形下网络空间全部为未知者时,引入一个网络舆情传播者所能影响人数的平均值。当基本再生数R0<1时,网络舆情不会大规模扩散;而当基本再生数R0>1时,网络舆情会呈现大规模扩散趋势。
定义x=(E(t),I(t),R(t),S1(t),S2(t))T,分别构造函数F(x)、V(x)、V(x)=V-(x)-V+(x)。其中,F(x)表示各类型中出现新增网络舆情传播者的概率,V+(x)表示由其他类型公众转变为该类型公众的概率,V-(x)表示由该类型公众转变为其他类型公众的概率,则有x′=F(x)-V(x)。根据式(9),有:
F(x)=αS1(t)I(t)+λS2(t)I(t)
βS1(t)I(t)+ξS2(t)I(t)
0
0
0(10)
V(x)=E(t)
-θE(t)+εI(t)
-γS1(t)I(t)-ηS2(t)I(t)-(1-θ)E(t)-εI(t)
S1(t)I(t)+δ′S1(t)-ζ′S2(t)
S2(t)I(t)+ζ′S2(t)-δ′S1(t)(11)
显然,当网络舆情不存在时系统处于稳定状态,此时网络空间仅存在两类未知者,即有E0=(0,0,0,S*1,S*2)为系统平衡点。由式(9)可知,S*1=ζ′/(δ′+ζ′),S*2=δ′/(δ′+ζ′)。F(x)、V(x)在E0处分别求导可得:
DF(E0)=F0
00, DV(E0)=V0
J1J2
其中:
F=0αζ′/(δ′+ζ′)+λδ′/(δ′+ζ′)
0βζ′/(δ′+ζ′)+ξδ′/(δ′+ζ′), V=10
-θε
则有:
FV-1=θ[αζ′/(δ′+ζ′)+λδ′/(δ′+ζ′)]εαζ′/(δ′+ζ′)+λδ′/(δ′+ζ′)ε
θ[βζ′/(δ′+ζ′)+ξδ′/(δ′+ζ′)]εβζ′/(δ′+ζ′)+ξδ′/(δ′+ζ′)ε(12)
可得FV-1的谱半径为:
R0=ρ(FV-1)=θ(αζ′+λδ′)+βζ′+ξδ′ε(δ′+ζ′)(13)
由式(13)可知,基本再生数与突发事件对异质风险感知公众的影响力以及公众风险感知水平交叉演变性具有密切关系,这些因素对网络舆情能否大规模扩散具有重要影响。其中,当其他因素保持不变时,若突发事件对异质风险感知公众的影响力β、ξ不断增大,使得基本再生数R0由小于1的值逐渐增大至1时,网络舆情逐渐扩散开来,且随着基本再生数R0的增大,扩散规模越来越大。
4 仿真分析
为了验证突发事件公众风险感知交叉演变下网络舆情传播S1S2EIR模型有效性,并进一步分析突发事件公众风险感知交叉演变下网络舆情传播规律,借助Matlab平台,以“北京新发地疫情”为例,通过实证数据对比研究与数值仿真进行分析。
4.1 S1S2EIR模型有效性分析
2020年6月11日北京新增1例新冠肺炎确诊病例,打破了北京长达57天无新增本地确诊病例的记录。6月12日报告显示新发地市场环境样本核酸检测呈阳性,且截至当天24时新增的多例本地新冠肺炎确诊病例均具有新发地市场活动史,致使“北京新发地疫情”成为舆论场讨论的热点。同时,由图4“知微事见”平台收集的参与“北京新发地疫情”突发事件讨论的微博用户地域分布图可以发现,不同地域的公众关注度存在较大差异,风险感知水平具有明显异质性。为此,本文以2020年“北京新发地疫情”为例,对S1S2EIR突发事件网络舆情传播模型有效性进行分析。如图5(a)所示,基于“知微事见”平台获取2020年6月11日—2020年7月3日期间有关“北京新发地疫情”事件的94 865条微博信息,以每日微博发文量变化情况表示相关网络舆情传播趋势。在S1S2EIR模型仿真中,结合现实情境令初始时刻网络舆情传播者I密度为0.001,由于此前国内新冠肺炎疫情已逐漸好转,故假设初始时刻高度风险感知未知者S1密度为0.1,低度风险感知未知者S2密度为0.899,其他状态公众密度为0。此外,由于严峻疫情形势的骤然而至,北京立即进入战时状态,公众面对疫情反弹也再次陷入恐慌,故这里设置各概率分别为α=0.2、β=0.7、γ=0.1、λ=0.3、ξ=0.4、η=0.3、θ=0.7、ε=0.3、δ′=0.3、ζ′=0.7,得到模型仿真结果,如图5(b)所示。对比图5(a)与图5(b)可以发现,S1S2EIR模型仿真结果与“北京新发地疫情”网络舆情真实数据传播趋势基本一致,因此模型具有有效性。
4.2 突发事件网络舆情传播过程分析
为了进一步分析突发事件网络舆情传播过程中各状态公众变化趋势,如图6所示,采用与4.1相同的参数设置,显示突发事件公众风险感知交叉演变下网络舆情传播过程。从图6可以看出,犹豫者E、传播者I的密度呈现先上升后下降的趋势,免
疫者R的密度呈现持续上升趋势。这3种状态变化趋势与前人研究成果基本一致。然而需要注意的是,对于同样处在未知状态的两类风险感知公众,二者密度变化趋势存在差异。其中,低度风险感知未知者S2的密度不断下降直到系统达到稳定状态,而高度风险感知未知者S1的密度呈现先上升后下降的趋势。这是因为初始时刻突发事件网络舆情信息尚未扩散开,仅有事发地等少部分公众知道突发事件且对具体信息尚不了解,构成最初的高度风险感知未知者。如“北京新发地疫情”爆发前夕,多地无新增本土病例,大部分公众将注意力集中在复工复产复学等方面,对疫情发展变化情况关注度较之前相对降低,对北京新发地疫情关注度更是少之又少,甚至很多非京公众此前尚未听过新发地农产品批发市场。因而当北京出现新增本土新冠肺炎病例时,只有患者周边极少部分公众为高度风险感知未知者。然而,伴随时间推移以及事件的发展变化,初期的低度风险感知未知者逐渐意识到问题严重性,因而在收到网络舆情信息前逐渐向高度风险感知未知者状态转移,致使高度风险感知未知者密度逐渐上升而低度风险感知未知者密度逐渐下降。如随着北京新增新冠肺炎病例的不断增加以及防控工作的立即开展,低度风险感知未知者逐渐转变为高度风险感知未知者。特别是新发地农产品批发市场吞吐量大,且伴随在新发地市场活动的非京籍患者以及四川、河北等地关联病例的出现,相关地区公众的风险感知水平也逐渐由低度向高度转移。然而,虽然整体呈现低度风险感知未知者转向高度风险感知未知者的演变态势,但这一过程中也存在未知者风险感知水平逆向演变的情况。如随着防控工作的有利开展,部分起初比较敏感的非疫区高度风险感知未知者会认为疫情暂时可控,加之期间我国多个省份遭遇台风、洪涝灾害,这些公众风险感知水平也可能由高度转为低度。此外,随着网络舆情信息传播扩散,越来越多公众得知相关信息,致使高度风险感知未知者与低度风险感知未知者密度均逐渐降低。当系统达到稳定状态时,网络中仅存在高度风险感知未知者、低度风险感知未知者以及免疫者3种状态的公众。
4.3 突发事件驱动的公众风险感知交叉演变对网络舆情传播的影响
4.3.1 突发事件对异质风险感知公众影响程度的作用分析
突发事件是公众感知到的主要风险源,事件特征是公众对突发事件风险判断并据此决定是否传播网络舆情的主要依据。为此,本节分析突发事件对高度风险感知未知者S1与低度风险感知未知者S2的影响,进而探索突发事件影响力对网络舆情传播的作用过程。由于传播概率β、ξ是刻画突发事件影响力的重要参数,传播者I密度最大值反映了网络舆情的最大影响,免疫者R密度最大值反映了网络舆情的最终扩散范围,故主要通过分析传播者I和免疫者R密度随传播概率β、ξ的变化情况研究突发事件影响力对网络舆情传播的作用。
这里假设初始时刻高度风险感知未知者S1密度为0.1,低度风险感知未知者S2密度为0.899,传播者I密度为0.001,犹豫者E与免疫者R密度均为0。图7、图8描绘了突发事件对高度风险感知未知者S1与低度风险感知未知者S2不同影响程度下,传播者I与免疫者R密度随时间的变化情况。其中,图7设置各参数分别为λ=0.2、ξ=0.4、η=0.4、θ=0.3、ε=0.5、δ′=0.5、ζ′=0.5;图8设置各参数分别为α=0.2、β=0.7、γ=0.1、θ=0.3、ε=0.5、δ′=0.5、ζ′=0.5。在图7中分别取α=0.3,β=0.6、α=0.2,β=0.7、α=0.1,β=0.8,代入式(13)計算可得基本再生数R0分别为1.15、1.22、1.29,则理论认为网络舆情会得到大规模扩散,这与图中所示结果一致。同理,在图8中分别取λ=0.3,ξ=0.3、λ=0.2,ξ=0.4、λ=0.1,ξ=0.5,代入式(13)计算可得基本再生数R0分别为1.15、1.22、1.29,理论上同样认为网络舆情会得到大规模扩散,与图中所示结果一致。同时,从图7、图8中还可以看出,传播者I、免疫者R密度最大值均随传播概率β、ξ的增大而增大,即突发事件对两类风险感知公众的影响程度越大,传播网络舆情的人数越多,最终得知网络舆情的人数也越多。
此外,为了进一步分析突发事件影响力对网络舆情大规模扩散的影响,图9显示了传播者密度最大值以及免疫者密度最大值随突发事件影响力β、ξ的变化。从图9可以发现,伴随突发事件对异质风险感知公众影响程度的变化,当基本再生数R0>1时,传播者密度最大值以及免疫者密度最大值将呈现迅速增长趋势。由此可见,突发事件影响力对网络舆情能否大规模扩散具有重要影响。
4.3.2 公众风险感知异质性对网络舆情传播的作用分析
公众风险感知水平及异质性体现了突发事件波及范围,对网络舆情传播过程具有重要影响。一般来说,与突发事件具有直接利益关系的公众通常具有较高的风险感知水平,而其他公众往往具有较低
的风险感知水平。显然,若公众风险感知异质性较低且普遍具有较高的风险感知水平,则表明突发事件波及范围较广。为此,用高度风险感知未知者S1与低度风险感知未知者S2的密度差异表示公众风险感知异质性,且当高度风险感知未知者密度较大时,表示突发事件波及范围较广,相反,当低度风险感知未知者密度较大时,表示突发事件波及范围较小。设置各参数分别为α=0.2、β=0.7、γ=0.1、λ=0.2、ξ=0.3、η=0.5、θ=0.3、ε=0.5、δ′=0.5、ζ′=0.5,分别分析传播者与免疫者的密度变化。
由图10可知,随着高度风险感知未知者密度的增大,突发事件网络舆情产生的最大影响与最终扩散规模均逐渐增大,且网络舆情扩散速率也不断增大。这说明公众风险感知异质性越低且高度风险感知未知者越多,突发事件波及范围越广,与之关联的网络舆情传播越快,影响范围越广。这一结果与现实情景是一致的,如图5(a)所示,2020年6月11日北京新增本土新冠肺炎病例1例,但由于各级卫健委网站往往在第二天发布疫情通报,且病例发现后需要多维度排查并不能立即锁定新发地市场,因而初始时刻并未引起公众较大关注,只有极少数公众处在高度风险感知未知者状态,“北京新发地疫情”舆情尚未迅速扩散。但随着疫情信息发布以及与新发地市场相关的新增本土病例的不断出现,公众逐渐产生恐慌情绪,“北京新发地疫情”网络舆情关注人数迅速增长,越来越多的低度风险感知未知者演变为高度风险感知未知者,6月13日新发地市场休市,网络舆情呈现迅猛增长,随后伴随疫情防控工作的迅速开展、新冠肺炎患者的救治以及北京疫情的好转,公众对“北京新发地疫情”网络舆情的关注度也逐渐降低。
4.3.3 突发事件驱动下公众风险感知交叉演变对网络舆情传播的作用分析
公众风险感知交叉演变与事态发展紧密相关,既可能受外界影响,随突发事件恶化与矛盾激化而逐渐上升,也可能随公众对事件可控性的了解以及问题解决而逐渐下降。这里假设初始时刻高度风险感知未知者S1密度为0.1,低度风险感知未知者S2密度为0.899,传播者I密度为0.001,犹豫者E与免疫者R密度均为0,设置各参数分别为α=0.2、β=0.7、γ=0.1、λ=0.3、ξ=0.3、η=0.4、θ=0.3、ε=0.4、δ=0.5、ζ=0.5。下面分别对事态逐渐恶化与事态逐渐好转两种情形进行讨论。
从图11可以看出,当不考虑突发事件驱动影响时,部分低度风险感知未知者会逐渐转变为高度风险感知未知者,致使网络舆情传播初期高度风险感知未知者密度逐渐增大。图11(a)显示了事态逐渐好转情形下各状态公众密度变化趋势,图11(b)显示了事态逐渐恶化情形下各状态公众密度变化趋势。由图11(a)可知,事态好转情形下随着突发事件驱动作用逐渐增强,公众风险感知交叉演变趋势发生转变,由低度风险感知未知者向高度风险感知未知者演变逐渐转换成由越来越多的高度风险感知未知者向低度风险感知未知者演变,致使低度风险感知未知者密度逐渐增大,并进一步削弱网络舆情产生的最大影响,降低网络舆情最终扩散规模。而与之相反,从图11(b)可以看出,事态恶化情形下随着突发事件驱动作用逐渐增强,公众风险感知交叉演变过程中越来越多的低度风险感知未知者会逐渐转变为高度风险感知未知者,致使高度风险感知未知者密度越来越大,并进一步强化网络舆情产生的最大影响,增大网络舆情最终扩散规模。此外,对比图11(a)与图11(b)还可以发现,突发事件驱动力度相同时,事态好转情形下突发事件驱动的公众风险感知交叉演变对网络舆情传播影响较大。这主要是因为大数据时代,网络空间信息量庞大且公众精力有限,若突发事件能迅速解决将不会引起大家广泛关注,且如今公众信息安全意识逐渐增强,当相关信息逐渐透明时,公众普遍不会轻信谣言并传播。
此外,为探究突发事件驱动下公众风险感知交叉演变程度对网络舆情传播的影响,本节还分析了两个公众风险感知交叉演变概率同步变化时,网络舆情最大影响程度以及最终扩散规模的变化趋势。这里假设初始时刻各状态公众密度不变,除公众风险感知交叉演变概率外其他参数设置同上。横坐标表示高度风险感知未知者演变为低度风险感知未知者的概率δ,纵坐标表示低度风险感知未知者演变为高度风险感知未知者的概率ζ′。图12(a)、图12(b)颜色值分别为网络舆情传播最大影响程度与网络舆情最终传播规模,且随颜色由蓝色变为黄色数值逐渐增大。
从图12可以看出,随着高度风险感知未知者演变为低度风险感知未知者概率δ′的增大,网络舆情最大影响程度以及最终扩散规模均会不断减小;与之相反,随着低度风险感知未知者演变为高度风险感知未知者概率ζ′的增大,网络舆情最大影响程度以及最终扩散规模均会不断增大。此外,根据图12(a)、图12(b)中对角线颜色变化情况可知,相同风险感知水平转移概率下,低度风险感知未知者演变为高度风险感知未知者所产生的影响大于高度风险感知未知者演变为低度风险感知未知者所產生的影响,致使网络舆情产生的最大影响及最终扩散规模随公众风险感知水平交叉演变概率的增大而逐渐增大。这一结果启示政府等有关部门应积极采取各种措施,第一时间尽全力解决突发事件及相关问题,及时公布相关信息消除公众疑虑,避免事件恶化造成公众风险感知水平提升及由此产生的次生衍生突发事件,有效引导公众理性思考,进而有效控制网络舆情大规模传播扩散,维护社会和谐稳定。
5 结 论
面对突发事件网络舆情,公众往往会结合自身所感知的风险并依据个人知识储备与经验阅历等决定是否传播。本文考虑公众对突发事件风险感知异质性与演变性双重特征,通过分析突发事件驱动的公众风险感知交叉演变机制,构建S1S2EIR突发事件网络舆情传播模型,并求解基本再生数。最后,以“北京新发地疫情”为例验证模型有效性,进而进一步通过数值仿真揭示突发事件公众风险感知交叉演变下网络舆情传播规律。研究发现:
1)突发事件对异质风险感知未知者的影响程度对网络舆情能否传播扩散具有重要作用,两类风险感知未知者受突发事件影响程度与网络舆情扩散规模及产生的最大影响呈正相关关系,且低度风险感知未知者受突发事件影响程度加大时对网络舆情传播过程的影响更大。
2)公众风险感知水平及异质性对突发事件网络舆情传播具有重要影响,公众风险感知水平越高且差异越小,表明突发事件波及范围越广,网络舆情产生的最大影响程度越大,最终扩散范围越广。
3)受突发事件发展趋势驱动影响,公众风险感知交叉演变对网络舆情传播具有重要作用。当突发事件逐渐恶化时,公众风险感知交叉演变过程中易由低度向高度转移,进而加剧网络舆情传播扩散。相反,当突发事件逐渐好转时,公众风险感知交叉演变过程中易由高度向低度转移,进而有助于抑制网络舆情大规模传播。
上述研究结果启示政府等有关部门,面对突发事件应立即响应,降低突发事件等级,削弱突发事件影响力,缩小突发事件波及范围,及时查明事情真相并适时公开,消除公众疑虑,降低公众风险感知水平,进而减小突发事件网络舆情产生的负面影响,维护社会和谐稳定。
参考文献
[1]Daley D J,Kendall D G.Stochastic Rumours[J].IMA Journal of Applied Mathematics,1965,1(1):42-55.
[2]Maki D P,Thompson M.Mathematical Models and Applications[M].Prentice-Hall,1973.
[3]Sudbury A.The Proportion of the Population Never Hearing a Rumour[J].Journal of Applied Probability,1985:443-446.
[4]Kawachi K.Deterministic Models for Rumor Transmission[J].Nonlinear Analysis:Real World Applications,2008,9(5):1989-2028.
[5]张亚明,苏妍嫄,刘海鸥.双重社会强化谣言传播模型及稳定性分析[J].系统科学与数学,2017,37(9):1960-1975.
[6]魏静,黄阳江豪,朱恒民.基于耦合网络的社交网络舆情传播模型研究[J].现代情报,2019,39(10):110-118.
[7]杨善林,周斌,贾焰,等.网络舆情监测、分析与管理的现状与挑战[J].中国工程科学,2016,18(6):17-22.
[8]李瑾颉,吴联仁,齐佳音,等.基于人类动力学的在线社交网络信息传播研究[J].电子与信息学报,2017,39(4):785-793.
[9]胡蓉,唐振贵,赵宇翔,等.移动经验取样法:促进真实情境下的用户信息行为研究[J].情报学报,2018,37(10):1046-1059.
[10]Centola D.The Spread of Behavior in an Online Social Network Experiment[J].Science,2010,329(5996):1194-1197.
[11]卢新元,胡智慧,易亚琦.融合用户信任及遗忘机制的社交网络传播预测模型[J].现代情报,2020,40(7):52-62.
[12]Romero D M,Meeder B,Kleinberg J.Differences in the Mechanics of Information Diffusion Across Topics:Idioms,Political Hashtags,and Complex Contagion on Twitter[C]//Proceedings of the 20th International Conference on World Wide Web.ACM,2011:695-704.
[13]郭强,岳强,李仁德,等.基于四阶奇异值分解的推荐算法研究[J].电子科技大学学报,2019,48(4):586-594.
[14]Hébert-Dufresne,Laurent,et al.Macroscopic Patterns of Interacting Contagions Are Indistinguishable from Social Reinforcement[J].Nature Physics,2020:1-6.
[15]Zhang L,Su C,Jin Y,et al.Cross-network Dissemination Model of Public Opinion in Coupled Networks[J].Information Sciences,2018,451:240-252.
[16]尚明生,邱晓刚.社会网络及其上的传播动力学集成研究[J].系统工程理论与实践,2015,35(10):2557-2563.
[17]王家坤,王新华.双层社交网络上的企业舆情传播模型及控制策略研究[J].管理科学,2019,32(1):28-41.
[18]赵海峰,孙艳秋,Edison T S E.基于有界信任模型的地铁突发事件信息传播[J].系统工程理论与实践,2017,37(12):3244-3252.
[19]刘小洋,何道兵.基于突发公共事件的信息传播动力学模型与舆情演化研究[J].计算机科学,2019,46(5):320-326.
[20]王治瑩,李勇建.政府干预下突发事件舆情传播规律与控制决策[J].管理科学学报,2017,20(2):43-52,62.
[21]种大双,孙绍荣.基于传染病模型的重大突发事件舆情传播与控制[J].情报理论与实践,2018,41(5):104-109.
[22]Yin F,Lv J,Zhang X,et al.COVID-19 Information Propagation Dynamics in the Chinese Sina-microblog[J].Mathematical Biosciences and Engineering,2020,17(3):2676-2692.
[23]Wang Z,Liang J,Nie H,et al.A 3SI3R Model for the Propagation of Two Rumors with Mutual Promotion[J].Advances in Difference Equations,2020,(1).
[24]Slovic P.Perception of Risk[J].Science,1987,236(4799):280-285.
[25]Afassinou K.Analysis of the Impact of Education Rate on the Rumor Spreading Mechanism[J].Physica A:Statistical Mechanics and Its Applications,2014,414:43-52.
[26]Chen S,Mao J,Li G,et al.Uncovering Sentiment and Retweet Patterns of Disaster-related Tweets from a Spatiotemporal Perspective—A Case Study of Hurricane Harvey[J].Telematics and Informatics,2019,47:101326.
[27]李钢,王聿达.基于受众画像的新型耦合社交网络谣言传播模型研究[J].现代情报,2020,40(1):123-133,143.
[28]Lü L,Chen D B,Zhou T.The Small World Yields the Most Effective Information Spreading[J].New Journal of Physics,2011,13(12):123005.
[29]Zheng M,Lü L,Zhao M.Spreading in Online Social Networks:The Role of Social Reinforcement[J].Physical Review E,2013,88(1):012818.
[30]阚佳倩,谢家荣,张海峰.社会强化效应及连边权重对网络信息传播的影响分析[J].电子科技大学学报,2014,43(1):21-25.
[31]Gomez Gardenes J,Latora V,Moreno Y,et al.Spreading of Sexually Transmitted Diseases in Heterosexual Populations.[J].Proceedings of the National Academy of Sciences of the United States of America,2008,105(5):1399-1404.
[32]Zan Y,Wu J,Li P,et al.SICR Rumor Spreading Model in Complex Networks:Counterattack and Self-Resistance[J].Physica A:Statistical Mechanics and Its Applications,2014,405:159-170.
(責任编辑:孙国雷)

