网络舆情演变过程的主体博弈及对策研究
孟骊超 来爽

收稿日期:2020-01-15
基金項目:陕西省提升公众科学素质计划项目(2020新型冠状病毒感染肺炎应急科普专项)“突发公共事件网络舆情的风险预防模型研究”(项目编号:2020PSL(Y)031);陕西省高等教育学会2020年“疫情防控专项研究课题”“突发公共事件下高校网络舆情的风险预模型研究”(项目编号:XGH20064)。
作者简介:孟骊超(1986-),女,硕士研究生,研究方向:电子政务、网络舆情。
通讯作者:来爽(1973-),男,副教授,博士,研究生导师,研究方向:网络信息安全、电子商务、电子政务、网络经济。
摘 要:[目的/意义]为探寻网络舆情演变的动力机制,本文采用演化博弈工具,试图厘清参与主体与舆情发展间的内在关联。[方法/过程]首先构建了网络舆情潜伏期、发展期、爆发期及消退期的演化博弈模型,通过求解博弈均衡和雅克比矩阵分析了网络舆情的演变路径和关联条件,以博弈主体之间的利益依存探讨了网络舆情发展演变的内在机制;在此基础上,在Matlab平台上对西安地铁3号线“问题电缆事件”舆情演变过程进行仿真模拟,并重点检验了心理满足程度对博弈均衡的影响。[结果/结论]处于不同发展时期的网络舆情,影响其未来走势的关键因素也有所不同;参与网络舆情的各方主体共同影响着舆情演变的方向;政府部门的作为对网络舆情影响重大;心理满足系数对网民的决策至关重要,甚至能够改变舆情事件的发展走向。
关键词:网络舆情;演变;主体博弈;仿真;心理满足
DOI:10.3969/j.issn.1008-0821.2020.12.012
〔中图分类号〕G206.2 〔文献标识码〕A 〔文章编号〕1008-0821(2020)12-0114-16
Research on the Actors Game and Countermeasures in the
Evolution Process of Internet Public Opinion
Meng Lichao Lai Shuang*
(School of Humanities,Economics and Law,Northwestern Polytechnical University,Xian 710072,China)
Abstract:[Purpose/Significance]In order to explore the dynamic mechanism to promote the evolution of Internet public opinion,this paper uses evolutionary game tools to clarify the internal relationship between the participants and the development of public opinion.[Method/Process]Firstly,the evolutionary game model of the incubation period,development period,outbreak period and recession period of Internet public opinion were constructed.By solving the game equilibrium and Jacobian matrix,the evolution path and associated conditions of Internet public opinion were analyzed,and the internal mechanism of the development and evolution of Internet public opinion was discussed based on the interest dependence between the players of the game.On this basis,on the MATLAB platform to“problem cable event”of Xian Metro Line 3 was simulated,and the effect of psychological satisfaction on game equilibrium was mainly tested.[Results/Conclusion]The key factors influencing the future trend of Internet public opinion in different development periods were also different;the main parties involved in the game jointly decided the direction of the evolution of Internet public opinion;the actions of government departments had a significant impact on the Internet public opinion;the number of psychological satisfaction factors was crucial to the decision-making of Internet users,and even could change the development trend of public opinion events.
Key words:internet public opinion;evolution;actors game;simulation;psychological satisfaction
网络舆情是当前理论界和政府高度重视的研究范畴,自2000年至今,国内研究成果遍及特征[1-3]、过程[4-5]、监测[6-7]、风险评估[8]、管理应对[9]等方面,但推动网络舆情发展演变的动力和本源究竟为何的问题,却没有得到有效解决。“天下熙熙,皆为利来;天下攘攘,皆为利往。”人类的逐利本性可以作为解释舆情演变的一个动因,用经济本源解释社会现象也符合辩证唯物主义的思想,因此,国内不少学者从利益博弈的视角出发,通过研究网络舆情的主体博弈过程,探寻推动舆情发展的动力机制和影响要素。
网民群体间博弈是研究的起点和热点,羊群效应[10-11]常被用以解释观点的收敛和演化过程,传染病模型[12-13]生动反映了网络舆情演变过程中网民的角色转化过程。政民博弈[14-15]则直观分析了舆情发展中政府与民众各自的利益关切点。而将网络媒体[16-17]、意见领袖[18]、网络推手[19]、企业[20]等主体纳入博弈过程,一方面是基于舆情主体多样化的现实需求;另一方面也有助于刻画企业舆情、伪舆情[21]等复杂多样的舆情传播过程。
不难发现,从系统角度分析群体行为调整的演化博弈理论将网络舆情的研究推向了行为逻辑的深度,得到的政策建议也更具有前瞻性和可操作性。但当前的研究大多使用一个博弈模型,侧重描述网络舆情的形成或爆发时刻,且主要关注博弈主体的一般收益,而对主体的心理满足程度缺乏有效关注。实质上,网络舆情的形成或爆发并非一蹴而就,是一个由量变到质变的过程,历经“生—老—病—死”的生命周期[22],仅仅使用一个模型描述舆情发展的全过程难免有失偏颇。而网络舆情的参与主体(人),作为感性与理性的复杂交织体,在考虑其经济收益的同时,对心理预期的考量也不容忽视。因此,对网络舆情演变全过程分别建模,通过博弈均衡探讨舆情发展的演化路径及影响条件,并考察心理满足程度对舆情发展的影响成为本文的主要研究内容。
1 网络舆情演变过程的阶段划分及博弈主体分析
依托现实情境,网络舆情的演变过程可以分为潜伏期、发展期、爆发期和消退期4个阶段,参与主体主要包括网民、网络媒体、意见领袖和政府4类,各主体的策略空间分别为{参与,不参与}、{报道,不报道}、{推动,不推动}以及{积极应对,消极应对}。同时,考虑到如果意见领袖的“推动”观点与网络媒体“报道”的观点相近,这两方主体的差异将十分微弱,可以视为同一主体进行考虑。为凸显博弈主体的差异性,本文假设意见领袖“推动”的观点显著不同于网络媒体“报道”的观点。
1.1 博弈主体收益分析
本文用一般效益和心理满足效益的代数和表示博弈主体的收益。一般效益包括经济效益、权威性和安全感等,如网络媒体的广告点击收益、意见领袖粉丝数量增加、网民社会地位提升等。同时,在不完全信息条件下,博弈方对一般效益的认知所產生的心理满足效益也会对其策略选择产生影响[23]。借鉴Bethwaite J等[25]考虑公平因素的效用函数,本文提出博弈主体的收益为:
Ui=ρi+βiρi-ρj(1)
其中,ρi和ρj表示博弈方i和j的一般收益;βiρi-ρj表示博弈方i的心理满足效益;βi∈[-1,1]为心理满足系数,反映博弈方i对一般效益差距的敏感程度或认知特点。βi从-1到1变化反映了博弈方i心理满足程度从最差到最优的过程。
1.2 网络舆情演变过程的主体组合
1.2.1 潜伏期的博弈主体组合
网络舆情的潜伏期是指事件的刺激性信息零星见于网络空间,表现为网民个体离散观点的点对点传播,尚未引起大规模关注和较大影响,博弈也主要发生于网民与网民之间。网民间博弈的收益矩阵及参数含义如表1和表2所示。由于博弈双方是同类型的,本文假设双方的一般收益相同时也具有相同的心理满足系数。表示双方策略不一致时各自的心理满足系数。
见领袖开始关注舆情事件,相关信息也开始不断被挖掘披露。意见领袖和网络媒体还利用强大的用户凝结力将网络空间划分成一个个“部落”,部落内部舆情更加快速地扩散并形成“热点话题”。在强势主体的推波助澜下,网络舆情快速发展传播,因此,发展期的博弈主要发生在意见领袖、网络媒体及网民之间,其收益矩阵及参数含义如表3和表4所示。
1.2.3 爆发期的博弈主体组合
网络舆情的持续发展可能会产生负面舆论,并通过线上线下共振严重影响社会和谐,因此社会管理者应该主动介入舆情发展,采取各项措施将负面影响降至最低。也就是说,政府将与由意见领袖、网络媒体及网民构成的大群体展开拉力。在相互博弈的过程中,舆情传播呈现出波浪式前进或螺旋式上升的状态,每当到达一个波峰或螺旋的顶部时,就出现了网络舆情的爆发。
在网络舆情的爆发期,处于中国政治生态下的网络媒体,大部分成为政府的“喉舌”,利用信息传播优势为政府“出声”并引导舆论方向,其博弈地位退化至政府一方。也有部分网络媒体作为网民利益的代表,继续与政府展开对话博弈,意见领袖的博弈地位也将发生同样的分化。因此这场博弈最终演变为政府与网民之间的公权力之争,其收益矩阵及参数含义如表5和表6所示。
1.2.4 消退期的博弈主体组合
历经爆发的舆情信息透明度已经非常高,加之网络中各种热点话题层出不穷,不断吸引着公众的
眼球,使得此次舆情逐渐淡出公众视野,但仍有零散信息可能在网民间默会传播,因此博弈也主要在网民之间展开。
与潜伏期不同的是,处于消退期的舆情信息带有很高的共识性,但舆情的消退并不意味着终结,如果此时出现了新的关联性刺激信息,将导致网络舆情重新进入发展期甚至引发次生舆情风暴。
2 网络舆情演变过程的博弈均衡分析
2.1 潜伏期网民—网民的博弈均衡分析
设网民群体选择“参与”策略的比例为x,则“不参与”的比例为1-x(0 U(参与)=x*(R1-C)+(1-x)*[R2-C+β1R1-C] U(不参与)=x*β2C-R2+(1-x)*0=x*β2C-R2 =x*U(参与)+(1-x)*U(不参与) F(x)=dxdt=x*(U(参与)-)=x*(1-x)*[x*(R1-C-β2C-R2)+1(-x)*(R2-C+β1R2-C)](2) 令F(x)=dxdt=0,可以求得该博弈最多存在3个稳定状态:x*1=0、x*2=1和x*3=R2-C+β1R2-CR2-R1-(β1+β2)R2-C(0≤x*3≤1)。对F(x)进一步求导得到: F′(x)=(1-2x)[x*(R1-C-β2C-R2)+(1-x)*(R2-C+β1R2-C)]+(x-x2)*[R1-R2-(β1+β2)C-R2] 令A=R2-C+β1R2-C,B=R2-R1-(β1+β2)R2-C,可以分情况求得网民博弈的进化稳定策略(ESS)。 1)当A>0且B>0时,x*3>1或x*3<0,所以x*3不是系统的稳定状态。此时F′(0)>0、F′(1)<0,故x*2=1是唯一的ESS。 2)当A<0且B<0时,x*3>1或x*3<0,所以x*3不是系统的稳定状态。此时F′(0)<0、F′(0)>0,故x*1=0是唯一的ESS。 3)当A>0,B<0时,0 4)当A<0,B>0时,0 当满足条件1时,无论对手是否“参与”网络舆情,博弈方“参与”策略的收益总是大于“不参与”的收益,因此会有越来越多的网民选择 网 民政府积极应对消极应对参 与R1-C1-F+β11R1+C2-C1-R2-2F,R2-C2+F+β21R2+2F+C1-C2-R1R1-C1+β12R1+C3+W2-C1,-C3-W2+β22C1-R1-C3-W2 不参与-W1+β13C2-W1-R2,R2-C2+β23W1+C2-R2(0,0) 参与网络舆情。羊群效应逐渐形成,博弈向着全体网民“参与”的均衡演化,其演化相位如图1(a)所示。 條件2则反映了与1相反的情形,由于博弈方选择“不参与”策略的收益更大,因此越来越多的网民将选择“不参与”策略,其均衡状态下的演 条件3表示:无论博弈方策略如何,其对手都将在相反策略下获得更大收益,此时博弈的均衡为:有x*3比例的网民选择“参与”网络舆情,1-x*3比例的网民选择“不参与”策略,其演化相位如图1(c)所示。 条件4与3的情况相反,博弈双方在相同策略下共同获得更多收益。此时博弈的均衡结果取决于网民参与网络舆情的初始比例x,当0 上述分析表明,在网络舆情的潜伏期,网民个体的策略会在一定程度上影响其他网民的选择。由于网民群体之间的学习和模仿行为,得益高的策略将受到网民群体的追捧,随着x和1-x比例的动态变化,网络舆情演变的方向也较为分散,既有可能消失无声,也有可能继续发展。 2.2 发展期网民—意见领袖—网络媒体的博弈均衡分析 随着网络舆情的扩散,一些强势节点逐渐参与其中。网络媒体、意见领袖和网民的三方博弈使网络舆情在发展期的演变更加复杂,任何一方的行动都会影响其他博弈方的策略选择,从而共同推进着网络舆情的传播。 在前文假设的基础上,进一步假设意见领袖选择“推动”策略的比例为y,网络媒体选择“报道”的比例为z,则网民、意见领袖和网络媒体选择“不参与”“不推动”“不报道”策略的比例分别为1-x、1-y和1-z(0≤x,y,z,1-x,1-y,1-z≤1)。由此得到网民在不同策略下的收益及复制动态方程分别为(为方便表达,省略心理满足系数的乘数项): U1(参与)=m1+y*z*(β11m1-m2-m3-β12m1-m2+W3-β13m1+W2-m3+β14m1+W2+W3)+y*β12m1-m2+W3+z*β13m1+W2-m3+(1-y-z)*β14m1+W2+W3 U1(不参与)=y*z*(β15-W1-m2-m3-β16-W1-m2+W3-β17-W1+W2-m3)+y*β16-W1-m2+W3+z*β17-W1+W2-m3-y*W1-z*W1+y*z*W1 F(x)=dxdt=x*(U1(参与)-1)=x*(1-x)*[y*z*(β11+β14+β16+β17-β12-β13-β15)+m1+y*(β12-β16)+z*(β13-β17)+(1-y-z)*β14+y*W1+z*W1-y*z*W1](3)
令F(x)=0,可得三方博弈的平衡点为x*=0、x*=1和
z*=-[y*(β12-β14-β16+m1+y*W1+β14][y*(β11+β14+β16+β17-β12-β13-β15)+(β13-β14-β17)+W1-y*W1]
当z=z*时,F(x)=0,此时无论x取值如何,博弈三方的收益均处于最大值,所有x均为ESS;当z>z*时,由于F(x)xx=0>0,F(x)xx=1<0,所以x*=1是ESS,即网民都会选择“参与”策略;当z
类似地,意见领袖和网络媒体的分析过程同理可证。经过分析,得到三方博弈系统可能存在的局部平衡点为(0,0,0)、(0,0,1)、(0,1,0)、(0,1,1)、(1,0,0)、(1,0,1)、(1,1,0)、(1,1,1)和(x*,y*,z*)(需滿足条件)。依据文献[25]提出的方法,通过分析系统雅克比矩阵的局部稳定性可以得到系统的ESS。具体地,需要先求出博弈系统的雅克比矩阵:
J=F(x)xF(x)yF(x)z
G(y)xG(y)yG(y)z
H(z)xH(z)yH(z)z
=(1-2x)Aa12a13
a21(1-2y)Ba23
a31a32(1-2z)C
其中,
a12=(x-x2)[z*(β11+β14+β16+β17-β12-β13-β15)+β12-β14-β16+(1-z)*W1]
a13=(x-x2)[y*(β11+β14+β16+β17-β12-β13-β15)+β13-β14-β17+(1-y)*W1]
a21=(y-y2)[z*(β21+β24+β26+β27-β22-β23-β25)+β22-β24-β26+(1-z)*W2]
a23=(y-y2)[x*(β21+β24+β26+β27-β22-β23-β25)+β25-β26-β27+(1-x)*W2]
a31=(z-z2)[y*(β31+β34+β36+β37-β32-β33-β35)+β33-β34-β37+(1-y)*W3]
a32=(z-z2)[x*(β31+β34+β36+β37-β32-β33-β35)+β35-β36-β37+(1-x)*W3]
A=y*z*(β11+β14+β16+β17-β12-β13-β15)+m1+y*(β12-β16)+z*(β13-β17)+(1-y-z)*β14-y*W1+z*W1-y*z*W1
B=x*z*(β21+β23+β26+β27-β22-β23-β25)+m2+x*(β22-β24-β26)+z*(β25-β26-β27)+β26+x*W2+z*W2-x*z*W2
C=x*y*(β31+β34+β36+β37-β32-β33-β35)+m3+x*(β33-β34)+y*(β35-β36)+(1-x-y)*β37+x*W3+y*W3-x*y*W3
再判断各平衡点处行列式DetJ和迹TrJ的正负,即可得到该博弈的ESS。不难算出博弈系统在各平衡点处行列式和迹的表达式如表7所示。
表7中,表达式(m1+β14)、(m2+β26)、(m3+β37)均反映了当前只有一方主体选择积极参与网络舆情,其余主体均选择消极策略的情形。表达式(m1+β11-β15+W1)、(m2+β21-β23+W2)、(m3+β31-β32+W3)代表博弈对手们均选择积极策略时,博弈方在不同策略下的收益差。例如:意见领袖和网络媒体选择“推动”和“报道”策略时,网民在两种策略下的得益差为:(m1+β11-β15+W1)。以上各表达式的正负需要分别进行讨论。
(m1+β13-β17+W1)、(m1+β12-β16+W1)表示意见领袖和网络媒体策略相左时,网民不同策略的得益差。例如:(m1+β13-β17+W1)代表意见领袖选择“不推动”,网络媒体选择“报道”时,网民是否参与网络舆情的收益差。结合第2节的分析,处于发展期的网络舆情,意见领袖和网络媒体分别代表持两种观点的强势主体,他们具有很强的引领力和号召力,当他们选择推动网络舆情时,网民大多积极参与,以期获得更多收益,因此推断该表达式的取值为正。
(m2+β25-β27+W2)、(m3+β35-β36+W3)代表网民选择“不参与”,在一方强势主体选择积极策略的情形下,另一方强势主体的策略收益差。网民是影响网络舆情发展最重要的力量,当一个强势节点选择积极策略但网民选择“不参与”时,推断网民不响应该强势节点。由于两方强势主体持相反意见,所以另一强势主体的积极策略必会获得网民支持,因此推断表达式取值为正。
(m2+β22-β24+W2)、(m3+β33-β34+W3)代表网民“参与”策略下,在一方强势主体选择消极策略时,另一方强势主体的策略收益差。在这种情形下,一方强势节点处于失声状态,广大网民缺乏精神领袖,另一方强势节点的积极策略将迅速引发网友热议,为其带来巨大收益,即表达式的取值为正。
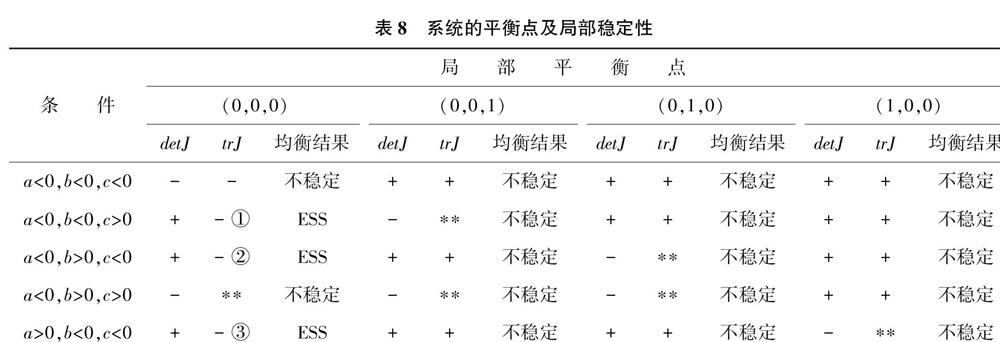
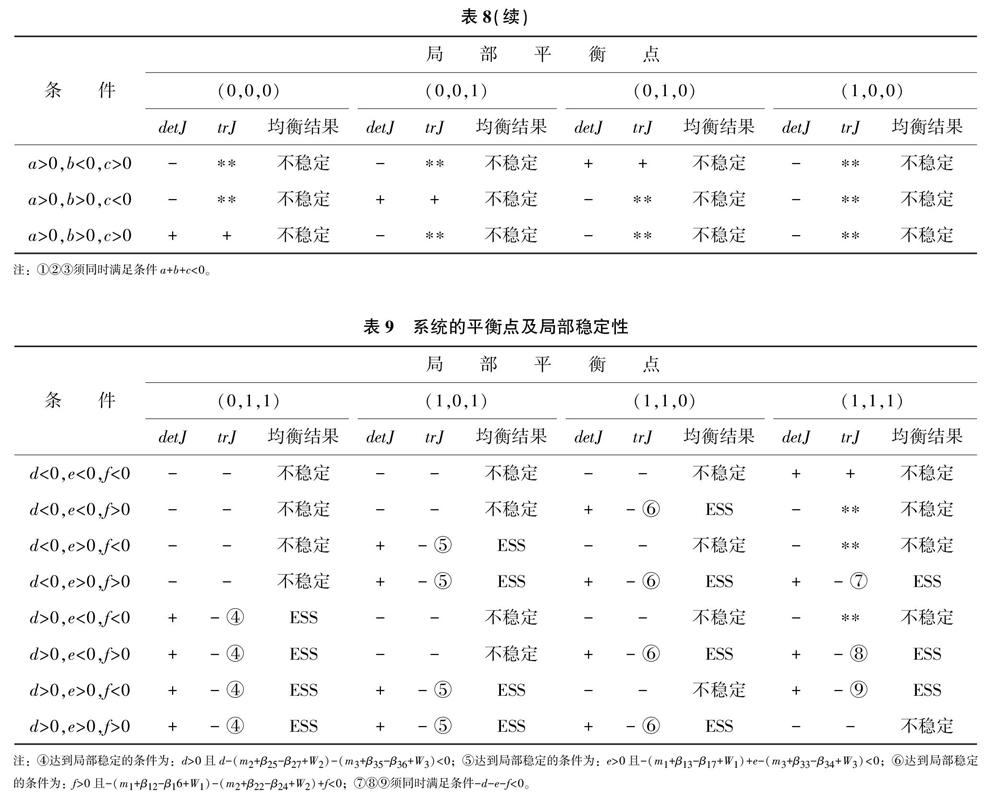
综合分析后发现行列式和迹的符号由表达式a=(m1+β14)、b=(m2+β26)、c=(m3+β37)、d=(m1+β11-β15+W1)、e=(m2+β21-β23+W2)和f=(m3+β31-β32+W3)的符号或符号组合决定。根据影响范围和所需条件不同,本文将行列式和迹的正负判断拆分为两个表格进行描述,具体见表8、表9。
由表8、表9可知,在网民—意见领袖—网络媒体的博弈中,当满足一定条件时,(0,0,0)、(0,1,1)、(1,0,1)、(1,1,0)和(1,1,1)都具有局部稳定性,是系统的进化稳定策略。
1)当满足条件a<0、b<0、c>0(或a<0、b>0、c>0或a>0、b<0、c>0)且a+b+c<0时,系统存在唯一的演化稳定策略(0,0,0)。这意味着博弈中只有一方主体选择积极策略并获得正收益,但其余两方均持消极态度,且博弈總收益为负。在这种情形下,无论各博弈方之前如何选择策略,(0,0,0)是系统唯一的ESS。以网民的决策为例,当意见领袖“不推动”且网络媒体“不报道”网络舆情时,网民仍然坚持“参与”策略,尽管此时网民仍可获得一定收益,但由于系统整体收益为负,最终导致网民孤掌难鸣,网络舆情将朝着网民“不参与”,意见领袖“不推动”,网络媒体“不报道”的均衡演进,其演化轨迹如图2(a)所示。
2)当满足条件d>0且d-(m2+β25-β27+W2)-(m3+β35-β36+W3)<0时,系统存在唯一的演化稳定策略(0,1,1)。这表示,当两方强势主体共同推进网络舆情时,网民“参与”获益更高。同时该均衡还需满足条件:网民的收益差小于情形①与情形②之和。情形①②分别指代一方强势主体选择积极推进舆情,但网民不参与时,另一强势主体的策略收益差。
满足上述条件时,系统的ESS为{不参与,推动,报道},其演化轨迹如图2(b)所示。
3)当满足条件e>0且-(m1+β13-β17+W1)+e-(m3+β33-β34+W3)<0时,系统存在唯一的演化稳定策略(1,0,1)。这意味着,当网媒和网民同时选择推动舆情时,意见领袖的积极策略获益更多。同时该均衡还需满足:意见领袖的收益差小于情形③与情形④之和。情形③④分别指代:在意见领袖的两个策略空间中,当网媒/网民选择积极策略时,另一方主体在不同策略下的收益差。此时系统的ESS为{参与,不推动,报道},其演化轨迹如图2(c)所示。
4)当满足条件f>0且-(m1+β12-β16+W1)-(m2+β22-β24+W2)+f<0时,系统存在唯一的演化稳定策略(1,1,0)。这一情形与均衡3类似,表明了在意见领袖的号召下网民积极参与网络舆情的现象,其演化轨迹如图2(d)所示。
均衡3、均衡4验证了第2节中描述的网络舆情发展期群体内部意见的形成与交流过程。在网络媒体或意见领袖的带领下,网络空间中形成了一个个相互独立的“部落”。由于网络媒体与意见领袖持相反意见,即使一方保持沉默,另一方也会推动网络舆情继续扩散。
5)当满足条件d<0、e>0、f>0(或d>0、e<0、f>0或d>0、e>0、f<0)且-d-e-f<0时,系统存在唯一的演化稳定策略(1,1,1)。这代表此时博弈的均衡取决于一方博弈主体的策略收益差与其他两方主体在“积极”策略下的收益组合。以网民的决策为例,当意见领袖和网络媒体同时选择“推动”和“报道”策略时,由于种种原因使得网民“不参与”获益更高,理性的网民选择置身事外,但另两方主体在积极策略下收获更多,所以他们仍然不断推送相关信息,最终也裹挟着网民选择“参与”策略。网络舆情朝着网民“参与”,意见领袖“推动”,网络媒体“报道”的均衡演进,网络空间众声喧哗,网络舆情逐渐从发展期辗转到爆发期。其演化轨迹如图2(e)所示。
综上所述,处于发展期的网络舆情其演化方向非常灵活。网民、意见领袖和网络媒体三者之间的策略选择相互作用、相互影响,任一参与主体的策略发生变化,都有可能改变网络舆情的演变方向。
2.3 爆发期网民—政府的博弈均衡分析
爆发期的网络舆情,假设政府在与网络媒体、意见领袖和普通网民集结而成的大网民群体进行博弈时,网民选择“参与”策略的比例为x,政府选择“积极应对”的概率为y。则“不参与”和“消极应对”的比例分别为1-x、1-y(0≤x,y,1-x,1-y≤1),此时网民及政府的复制动态方程分别为(各主体的期望收益函数参前文):
F(x)=dxdt=x*(U1(参与)-1)=x*(1-x)*[y*(W1-F+β11R1+C2-C1-R2-2F-β12R1+C3+W2-C1-β13C2-W1-R2)+(R1-C1+β12R1+C3+W2-C1)](4)
G(y)=dydt=y*(U2(积极应对)-2)=y*(1-y)*[x*(F+C3+W2+β21R2+2F+C1-C2-R1-β22C1-R1-C3-W2-β23W1+C2-R2+(R2-C2+β23W1+C2-R2)](5)
令F(x)=0,G(y)=0,可分别求得博弈各方的稳定状态,并获得系统可能存在的局部平衡点分别为(0,0)、(0,1)、(1,0)、(1,1)以及(x*,y*)(需满足条件0≤x*、y*≤1),解得系统的雅克比矩阵为:
J=F(x)xF(x)y
G(y)xG(y)y=A(1-2x)B(x-x2)
C(y-y2)D(1-2y)
其中,
A=y*(W1-F+β11R1+C2-C1-R2-2F-β12R1+C3+W2-C1-β13C2-W1-R2)+(R1-C1+β12R1+C3+W2-C1)
B=W1-F+β11R1+C2-C1-R2-2F-β12R1+C3+W2-C1-β13C2-W1-R2
C=x*(F+C3+W2+β21R2+2F+C1-C2-R1-β22C1-R1-C3-W2-β23W1+C2-R2)+(R2-C2+β23W1+C2-R2)
D=F+C3+W2+β21R2+2F+C1-C2-R1-β22C1-R1-C3-W2-β23W1+C2-R2
各局部平衡点处的detJ和trJ的表达式见表10。
分析表10可知,行列式和迹的符号由a=(R1-C1+β12R1+C3+W2-C1)、b=(R2-C2+β23W1+C2-R2)、c=(R1-C1-F+β11R1+C2-C1-R2-2F+W1-β13C2-W1-R2)、d=(R2-C2+F+C3+W2+β21R2+2F+C1-C2-R1-β22C1-R1-C3-W2)的符号及符号组合决定。a代表政府消极策略下网民“参与”的收益;b表示网民“不参与”舆情时政府“积极应对”的收益;c表示政府“积极应对”时网民的策略收益差;d表示网民“参与”舆情时政府的策略收益差。
进一步分析发现:在网络舆情的爆发期,各种信息充斥于网络空间,谣言与真相齐飞,不断裹挟着更多不明真相的网民参与其中,在“沉默的螺旋”和“群体极化”效用下,极易引发极端言论甚至极端行动,严重威胁着社会秩序和公共安全。此时政府若采取消极放任策略,将导致网络舆情愈发不可收拾,只有“积极应对”才有可能平息舆论,将损失降至最低,因此推断d>0。
另一方面,当政府部门选择“消极应对”网络舆情时,在宽松的监管环境下,网民更倾向通过“参与”传播舆情收获更多的关注度和心理满足感,故a>0。
综上所述,各平衡点上行列式和迹的符号需要根据b和c的正负分别进行讨论,具体情况如表11所示。
局部平衡点b>0,c>0b>0,c<0b<0,c>0b<0,c<0detJtrJ均衡结果detJtrJ均衡结果detJtrJ均衡结果detJtrJ均衡结果
(0,0)++不稳定++不稳定-**不稳定-**不稳定
(0,1)-**不稳定+-ESS++不稳定-**不稳定
(1,0)-**不稳定-**不稳定-**不稳定-**不稳定
(1,1)+-ESS-**不稳定+-ESS-**不稳定
(x*,y*)不是局部平衡点不是局部平衡点不是局部平衡点+-鞍点
由表11可得(0,1)和(1,1)具有局部稳定性,是当前博弈的ESS。
1)当b>0且c>0时,系统存在唯一的演化稳定策略(1,1)。这表明博弈双方的积极参与都能为自身带来更高收益时,系统的演化稳定策略为{参与,积极应对},其演化轨迹如图3(a)所示。
2)当b>0且c<0时,系统存在唯一的演化稳定策略(0,1)。这意味着政府“积极应对”舆情不仅使自身获益为正,而且使网民的“不参与”策略获益更高时,博弈的演化稳定策略为{不参与,积极应对}。此时,网络舆情也将逐渐转至消退,其演化轨迹如图3(b)所示。
3)当b<0且c>0时,系统存在唯一的演化稳定策略(1,1)。与条件1类似,此时博弈将朝着网民“参与”和政府“积极应对”的均衡演变,网络舆情呈持续爆发态势,其演化轨迹如图3(a)所示。
对爆发期的分析发现,只有政府积极应对并使网民认识到继续“参与”必然得不偿失,公众才有可能慢慢平静下来,舆情也才能日渐消退。
2.4 消退期网民—网民的博弈均衡分析
网络舆情消退期的主体博弈也发生于网民和网民之间。但与潜伏期不同的是,历经发展和爆发的网络舆情,各类信息的透明度已经很高,网民此时选择“参与”的获益大大降低,甚至還可能在政府的惩罚举措下得不偿失。即消退期网民间的博弈均衡符合2.1节中的条件2,博弈最终会朝着全体网民选择“不参与”的均衡演化,网络舆情慢慢归于平静。
3 案例仿真与分析
为验证上述理论研究的有效性,本章以2017年西安地铁3号线“问题电缆事件”为例进行分析。通过对该事件网络舆情演变过程进行仿真,验证了舆情传播过程中的主体博弈,并考察了心理满足程度对博弈均衡的影响。
3.1 案例梳理
西安地铁3号线2012年开工,2016年8月正式开通运营。2017年3月13日,1名网友在天涯论坛发表贴文《西安地铁你们还敢坐吗》,称地铁3号线整条线路所用的电缆偷工减料,陕西奥凯电缆有限公司以次充好,将不合规格的电缆提供给施工方,相关信息零星传播于网友之间,网络舆情处于潜伏期。3月15日起,该贴开始广泛传播并引发公众热议,陕西奥凯电缆有限公司(意见领袖)发布多份澄清声明,网络媒体也积极报道,推动舆情快速发展。3月16日晚23:50分,西安市政府正式回应事件,其后连续发布通告持续引爆全网,网络舆情呈现爆发态势。3月23日起,随着对责任人的处理及对全国范围内涉事电缆排查工作的展开,网络舆情开始慢慢消退。
3.2 “问题电缆事件”网络舆情演变过程的仿真
在对事件梳理的基础上,采用Matlab2010对网络舆情的演变过程进行仿真有助于检验理论的可靠性。结合实际情况,同时不失一般性,对各阶段博弈主体成本收益的赋值见表12,此次网络舆情事件演变过程的仿真效果图分别如图4~8所示。
以上图例反映了参与主体策略选择的概率变化,也再现了“问题电缆事件”网络舆情演变的全过程。潜伏期越来越多网民的“参与”推动舆情进入发展期,意见领袖、网络媒体和网民的三方博弈促使网络舆情开始爆发,随后在政府的积极应对下,网民的热情逐渐消退,舆情也归于消退期。
3.3 “问题电缆事件”博弈主体的心理满足系数对博弈均衡的影响
现有研究大部分都从博弈主体的一般收益出发,考察经济效益对舆情演变的影响,心理满足程度对舆情演变影响的文献尚不多见,因此本文希望探明心理满足系数与舆情演变的内在关联。
如1.1节所述,βi代表博弈主体的心理满足程
度,本文设置-1、0和1这3个取值,分别反映主体的心理满足程度最差、无影响和最优。同时考虑到博弈主体在不同策略组合中具有不同的βi,为定向考察某一主体的心理满足系数,假设其他主体的心理满足程度不会影响博弈均衡,即将其余βi设置为0。
在“问题电缆事件”网络舆情的潜伏期,需要考察网民策略相异时“参与者”的心理满足系数β1和“不参与者”的心理满足系数β2。如图9所示,观察β1对曲线的影响:随着β1从大到小变化,曲线的收敛速度也逐渐变缓,即随着“参与者”心理满足程度的降低,其“参与度”也随之降低。此外,当β1-β2取最大值时,心理满足系数对博弈均衡的影响最大,对应曲线③④。也就是说,当两种策略的心理落差最大时,βi较大的一种策略将成为主流选择,参与者的热情愈加高涨,而不参与者则愈加消极,最终推动网络舆情朝不同的方向发展。
图9 “问题电缆事件”网络舆情潜伏期心理满足系数对博弈均衡的影响
图10分别考察了网络舆情发展期网民、意见领袖和网络媒体在不同策略组合中的心理满足系数。由图形可知,β此时对博弈的影响比较微弱,但当其余两方选择阻滞策略,仅考察方选择推动策略时,βi仍能在一定程度上影响博弈均衡的演化路径。以网民的策略为例,如图10(a)所示中β14,β14=-1及β14=1时,分别对应了最慢和最快的曲线收敛速度。这表明,在不改变三方博弈其他参数的基础上,即使已经有两方选择阻滞策略,但剩余一方在心理满足程度的驱使下依然积极参与,这将会使政府减缓舆情传播的预期落空。意见领袖和网络媒体的相应参数分别为图10(b)中的β26和图10(c)中的β37。
网络舆情进入爆发期后,网民的心理满足程度可能会改变他们的最终选择,但政府部门的心理满足系数只能加速或减缓其选择积极策略的速度,并不能改变政府积极应对舆情事件的决心。
如图11(a)所示,曲线②(β11=1)、③(β11=-1)反映了政府“积极应对”网络舆情时,心理满足程度高的网民具有更强的参与意愿,表现为曲线的收敛速度更快。曲线④⑤反映了政府的消极应对“激发”了网民的参与热情,此时曲线具有更加陡峭的斜率。政府如果希望网民改变策略,就必须提升网民“不参与”时的心理满足程度。如曲线⑥所示,当网民认为“不参与”策略能获得最佳心理满足时,即使仍有部分网民略有“挣扎”,最终的博弈均衡总会朝着全体网民“不参与”的方向演变。
政府部门积极处置爆发的网络舆情是其义不容辞的责任和义务,因而无论如何调整心理预期,这个总趋势不会发生改变。但图11(b)也反映出当网民选择不参与舆情传播时,政府的心理满足落差也影响着博弈均衡的收敛速度(曲线⑥⑦)。
随着舆情的持续发展,事件的透明度越来越高,使得即使在高心理满足系数下,网民的整体收益依然很低,最终全体网民选择了“不参与”,图12(a)反映了这一过程。但曲线②⑦又印证了网络舆情具有“死灰复燃”的可能性,这提醒政府部门:即使在网络舆情的消退期,仍要对网民的心理满足保持关注以避免舆情风暴的重新爆发。
如图12(b)所示,当“问题电缆事件”网络舆情重新归于网民之间的博弈时,尽管此时舆情传播已经日暮西山,但心理满足程度仍深刻影响着博弈的均衡路径,网络舆情也存在死灰复燃的可能(曲线②④)。同时,心理满足系数也影响网络舆情的消退时间和速度。
4 研究结论与应对策略
4.1 研究结论
本文主要研究了网络舆情演变过程的主体博弈。文章分别构建了潜伏期、发展期、爆发期及消退期的演化博弈模型,通过求解博弈均衡和雅克比矩阵分析了网络舆情的演变路径和关联条件,以主体之间的利益依存探讨了网络舆情演变的内在动力。在此基础上,以2017年西安地铁3号线“问题电缆事件”为实例背景,在Matlab平台上对舆情演变的全过程进行了仿真模拟,又重点考察了心理满足系数对博弈均衡的影响,最后得到了本文的研究结论。
1)从博弈的视角分析网络舆情的演变,不难发现由于每个时期主要参与主体及其收益的差异化,使得影响舆情发展的关键因素也有所不同。如在网络舆情潜伏期,网民是主要参与主体,其获益的多寡决定了舆情的未来走势;而随着网络媒体、意见领袖等强势节点的加入,舆情信息快速在网络空间蔓延辐射,这些强势节点理应成为政府治理舆情的关键所在。
2)参与博弈的各方主体共同影响着舆情的演化方向。网民、政府、意见领袖及网络媒体之间的策略选择彼此交织,相互影响。任意一方行动的调整都会改变系统内其他主体收益,从而改变舆情的演变方向。例如,在舆情的发展期,1.2节中的均衡1反映了当意见领袖和网络媒体均选择不推动策略时,网民的坚持“参与”最终也将不了了之,系统的ESS仍为{不参与,不推动,不报道}。与此对应,均衡5则代表了相反的情况,在意见领袖及网络媒体的推动下,原本“不参与”的网民最终也投入到网络舆情的洪流之中。
3)通过博弈分析发现政府策略对网络舆情影响重大。在网络舆情演变的过程中,政府部门的所作所为将深刻影响甚至改变舆情的演化方向。例如,若政府在舆情的潜伏期就采用“发布权威信息”“惩治谣言”等举措,网络舆情很可能被遏制于摇篮之中;或者当网络舆情爆发时,政府若依然采取消极懈怠的处理方式,无疑会刺激网民热议并形成更大的舆论漩涡,造成不可挽回的严重后果。
4)收益多寡是決定博弈主体策略选择的直接动因,其心理满足程度也不容忽视。博弈主体的收益由一般效益和心理满足效应构成,前者主要取决于经济要素,后者则与博弈方的内心感知相关,如社会关注度的提升、情绪宣泄等。通过对“问题电缆事件”网络舆情演变的仿真发现,心理满足系数深刻影响着网民的行动,直至改变舆情事件的发展走向。在网络舆情的潜伏期,心理满足程度直接决定了舆情信息的传播速度,而位于消退期的网民心理满足程度,则可能使原本已经趋于平静的网络舆情重新沸腾起来。
4.2 應对策略
基于研究结论,本文提出了政府应对网络舆情演变的策略和建议:
1)面对汹涌的网络舆情,政府要冷静面对,准确判断舆情发展阶段,并据此确认主要参与主体,有的放矢调整各方收益,主动规划网络舆情的发展方向。
2)由于博弈各方的策略选择息息相关,因此,政府需要综合调控各方收益。一般来讲,政府在治理网络舆情时,首先要考虑的是数量巨大的网民群体,他们是掀起舆论风暴的“关键力量”,因而降低网民参与率是政府平息网络舆情的重要抓手。但本文研究证实,如果进一步挖掘出博弈系统中其他参与主体与网民的内在利益关联,找到影响网民策略选择的内生桥梁,通过团结意见领袖及网络媒体,就可以达到事半功倍的治理效果。
3)政府部门的积极主动和灵活权变是应对网络舆情的“金钥匙”。首先,政府部门及时发声、积极回应等主动行为都能引导网络舆情积极发展。政府部门直面网络舆情,向民众传递的是一种主动负责的态度,构建了解决问题的良好开端。而正面回应网民关切,及时公布调查真相则减少了滋生谣言的土壤,让网民理智对待舆情事件。严肃追责问责则有利于强化政府正面形象,增进官民信任。其次,在网络舆情发展的不同时期,政府要保持灵活权变。由于政府需要应对的参与主体及其利益诉求各有不同,因此要求政府务必保持权变的态度,因事因时制宜,灵活调整应变举措,提高政府部门网络舆情管理的质量和效率。
4)加强心理学理论在舆情治理方面的运用,通过调整网络舆情参与主体的心理预期,达到舆情治理的目的,不断提高政府舆情应对的手段和水平。一般来说,网络舆情事件大多与民生密切相关,因而受到事件内生公共危害性和社会正义感的驱动,网民群体很容易在心理效应的催化下积极传播舆情。“上兵伐谋”,政府部门要在深入总结网络舆情演变规律的基础上,从行为主体的策略选择逆向推导出影响其抉择的心理要素,透过现象抓本质,找准网民的心理关切点再对症下药,通过调整博弈方的心理满足程度疏散网络舆情。
参考文献
[1]匡文波,周倜.2018年网络舆情的特征研究[J].新闻与写作,2019,(2):79-83.
[2]李明德,张玥,张琢悦,等.2014—2017年雾霾网络舆情现状特征及发展态势研究——以新浪微博的内容与数据为例[J].情报杂志,2018,37(12):112-117.
[3]赵丹,王晰巍,韩洁平,等.区块链环境下的网络舆情信息传播特征及规律研究[J].情报杂志,2018,37(9):127-133,105.
[4]顾雨迪,狄岚.分层演化趋向行为的网络舆情传播模型[J].智能系统学报,2018,13(5):700-706.
[5]黄炜,余辉,李岳峰,等.网络舆情事件演化的仿真实践研究[J].现代情报,2017,37(8):65-73.
[6]张艳丰,李贺,彭丽徽.基于直觉模糊推理的网络舆情监测预警评估方法研究[J].情报杂志,2017,36(6):111-117,172.
[7]宋余超,陈福集.基于数据立方体的网络舆情监测指标体系构建[J].情报科学,2016,34(6):31-36.
[8]梁冠华,鞠玉梅.基于舆情演化生命周期的突发事件网络舆情风险评估分析[J].情报科学,2018,36(10):48-53.
[9]张玉亮,杨英甲.基于4R危机管理理论的政府网络舆情危机应对手段研究[J].现代情报,2017,37(9):75-80,92.
[10]刘锦德,刘咏梅.基于不完全信息演化博弈模型的网络舆情传播羊群行为[J].国防科技大学学报,2013,35(5):96-101.
[11]陈福集,黄江玲.基于演化博弈的网络舆情传播的羊群效应研究[J].情报杂志,2013,32(10):1-5.
[12]魏静,朱恒民,洪小娟,等.基于复杂在线网络的舆情传递研究——进化博弈视角[J].现代图书情报技术,2013,(3):65-70.
[13]祁凯,杨志,张子墨,等.政府参与下网民舆论引导机制的演化博弈分析[J].情报科学,2017,35(3):47-52.
[14]刘人境,孙滨,刘德海.网络群体事件政府治理的演化博弈分析[J].管理学报,2015,12(6):911-919.
[15]霍良安,邵洋洋.基于秩依效用理论的网络舆情传播博弈模型[J].现代情报,2016,36(9):45-49.
[16]周 飞,郭韧.基于多方博弈的政府回应网络舆情策略研究[J].情报杂志,2015,34(5):128-133.
[17]董凌峰.基于SD演化博弈的网络舆情形成阶段主体研究[J].情报科学,2018,36(1):24-31,44.
[18]王澍贤,陈福集.意见领袖参与下微博舆情演化的三方博弈分析[J].图书馆学研究,2016,(1):19-25.
[19]魏芳芳,陈福集.网络虚假信息中政府、企业和公民三者的进化博弈行为分析[J].运筹与管理,2012,21(6):225-230.
[20]陈福集,黄江玲.三方博弈视角下政府应对网络推手的对策研究[J].中国行政管理,2013,(11):18-21.
[21]赵静娴.演化博弈视角下的网络伪舆情监管对策研究[J].情报科学,2016,34(6):143-146,169.
[22]李昊青,兰月新,侯晓娜,等.网络舆情管理的理论基础研究[J].现代情报,2015,35(5):25-29,40.
[23]李勇建,王治莹.突发事件中舆情传播机制与演化博弈分析[J].中国管理科学,2014,22(11):87-96.
[24]王长春,陈超.基于复杂网络的谣言传播模型[J].系统工程理论与实践,2012,32(1):203-210.
[25]Bethwaite J,Tompkinson P.The Ultimatum Game and Non-selfish Utility Functions[J].Journal of Economic Psychology,1996,17(2):259-271.
[26]Friedman D.Evolutionary Game in Economics[J].Econometrica,1991,59(3):637.
(责任编辑:孙国雷)

