风电场中电力无源滤波器设计与优化策略

赖迎 涂继昭

国家电投集团江西电力有限公司高新清洁能源分公司 江西南昌 330000

在风电系统的应用和发展中，随着电场容量的不断扩大，风电场并网给系统电力带来的影响也越来越大，其中，一个最主要的影响就是电力谐波。因此，在具体的风电系统应用过程中，风电企业应加强对电力谐波的重视，并通过无源滤波器的合理设计和优化来提升谐波治理效果，以此来保障风电系统的正常运行，在满足用户需求的基础上提升风电企业经济效益。

1 风电场电力无源滤波器的设计分析

在对风电场内的无源滤波器进行设计时，基本应该遵循以下的几个设计步骤：

在滤波器加装之前，应该对风电网络中的谐波情况进行全面分析，以此来获得各次的谐波电流和谐波电压等的这些计算数据。

对风电系统所需要的滤波器机组以及无功补偿容量进行安装方案的初步确定。在对风电系统中的无功补偿容量进行计算的过程中，主要可通过估算法来进行容量Q 的估算。假设在滤波器加装之后，系统中的功率因数取值需要根据实际的工作情况来进行确定，则可以通过以下公式来进行容量Q 的估算：

在以上公式中，风电系统中的有功负荷用P 表示，滤波器加装之前的系统功率因数角用 0φ 表示，加装之后的因数角用 1φ 表示。

在对滤波器机组进行安装的过程中，其具体的安装方案和风电网络谐波源及其谐波分析有着直接关系。通常情况下，在风电场中，谐波源都属于变流器。比如，在六脉整流形式的变流器中，就可以进行5 次和7 次单调谐波器的装设，如果依然存在频率比较高、幅值比较低的很多谐波，则需要将一组高通滤波器设置在系统中，其调谐作用通常在7-12 次[1]。

按照相应的计算结果进行无源滤波器机组中每一个滤波器实际参数的计算。首先是单调谐波形式的滤波器计算，在具体计算中，通过调谐次数、电容器的额定电压以及n 次谐波电流来进行电容量Qc 的确定，最后再对电容C、电阻R 以及电感L 进行求解，其具体计算公式如下：

在以上公式中，电容器自身的额定电压用UN表示，第n 次谐波产生的电流值用In表示，基波角频率用 0ϖ 表示，调谐锐度用Q表示。

其次是高通谐波器，通常情况下，这种谐波器需要设定更大一些的容量，以此来降低高通谐波器自身的损耗。但是容量也不可太大，这样才可以有效避免无功功率出现过补偿现象，防止电力事故。在确定了单调形式的谐波器参数之后，就可以对高通滤波器进行基波无功输出的计算，假设无功输出是Q（H），在具体计算中，可通过以下公式进行计算：

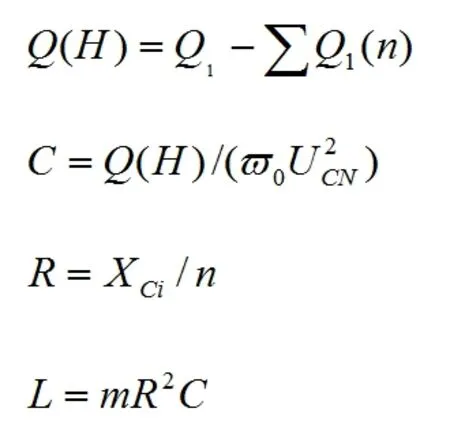
校验选择的电压以及电流参数，如果发现参数不符合实际需求，则需要对其再一次调整并校验，一直到完全与实际运行过程中的安全要求相符为止。

2 风电场无源滤波器的优化

2.1 等式约束条件

在对风电系统的无源滤波器进行设计的过程中，主要的等式约束条件就是系统滤波网络方面的潮流方程。通过算例来看，假设滤波源等值阻抗是Zeq，对没有频偏状态下的基波以及谐波潮流方程进行建立，其公式如下：

2.2 不等式约束条件

在对风电系统的无源滤波器进行设计的过程中，主要的不等式约束条件就是根据相关规定对总谐波含量以及系统谐波含量进行允许值的计算。首先是对35KV 单次谐波电压含量不超过公用电网谐波含量最大允许值的情况进行计算，以下是其计算公式：

在以上公式中，当母线为35KV 条件下，电压总谐波畸变率的具体规定值用D 表示。

2.3 目标函数的优化

首先是谐波抑制方面目标函数的优化，具体优化过程中，可通过传统方法对实际的滤波效果进行衡量，也就是保障滤波总畸变率最小，其公式如下：

其次是无功补偿方面目标函数的优化，在无源滤波器中，无功补偿方面的容量不仅需要保障系统功率因数与1 接近，同时又要保障不出现过补偿情况，因此有：

在以上公式中，风电系统的无源滤波器所能提供的最小基波无功用Qmin 表示，这个无功功率可以满足风电系统最低的功率因数需求；风电系统的无源滤波器所能提供的最大基波无功用Qmax 表示，这个无功功率可以让风电系统中的功率因数和1 无限接近[2-3]。

因为对风电系统中的无源滤波器进行参数优化是一个非线性过程，且有着很多的优化目标，所以在具体的优化过程中，风电企业可借助于MATLAB 形式的优化工具箱来进行优化，以编程的形式来对风电系统中的无源滤波器进行参数优化。通过这样的方式，就可以让无源滤波器获得良好的优化效果。

3 结语

综上所述，在风电行业的不断发展中，随着电网的扩展和并网等工作的开展，系统谐波情况也越来越常见。在对风电系统谐波进行治理的过程中，无源滤波器是一种主要的治理设备。所以，风电企业应该加强对无源滤波器的设计及其参数优化。通过这样的方式，才可以让风电系统谐波问题得以有效治理。