基于变步长Velocity Verlet 算法的卢瑟福散射模拟的优化

周 伟，张宜新，刘学锋，杨喜峰，王殿生，王玉斗

（中国石油大学（华东） 理学院，山东 青岛 266580）

卢瑟福散射是近代物理科学发展史上一个非常重要的实验。该实验验证了原子的核式模型，奠定了原子物理学的基础[1-2]。同时，卢瑟福散射还推动了许多技术应用方面的进步。例如：利用离子束与物质相互作用对物质进行元素成分分析和结构分析的离子束分析技术[3]；利用卢瑟福散射中的大角度偏转进行物质分析的背散射技术[4]等。

由于卢瑟福散射有着很高的技术价值，因此它一直保持着较高的研究热度。计算机模拟是一种常用的研究卢瑟福散射的方法。目前，国内外有许多关于计算机模拟卢瑟福散射的研究。文[5—6]中，作者直接应用卢瑟福散射公式计算了单靶核对α 粒子的散射几率。然而这种方法无法模拟出α 粒子的运动情况，更无法研究实际散射过程中存在的多靶核的影响。文[7]中，作者利用Visual Basic 语言完成了卢瑟福散射轨迹的模拟，模拟出了不同α 粒子入射能量和瞄准距离下的α 粒子散射的运动轨迹。但其主要内容是单个粒子散射轨迹的演示，并没有讨论散射几率。文[8—9]中，作者利用欧拉方法与蒙特卡罗方法模拟了散射过程，既模拟了散射的运动轨迹，又得到了散射概率曲线。但是，当靶核数目较多或模拟次数较大时，文中所使用的程序出现了效率低、计算时间长的问题，难以满足研究要求。

目前，卢瑟福散射的计算机模拟效率低主要有两方面原因：一是核心算法的精度偏低，导致了单位步长较小；二是模拟中没有考虑不同条件下粒子受力的变化，采用了单位步长固定的模拟方法。鉴于以上不足，本研究基于文[9]中所使用的模拟框架，采用了新的优化算法，并在此基础上引入了动态步长，大幅度提高了卢瑟福散射的模拟效率。

1 模拟方法

首先介绍本文中进行卢瑟福散射的计算机模拟的基本流程，然后详细介绍几种轨迹模拟算法的原理并比较其效率，最后给出提高模拟效率的变步长处理方案。

1.1 模拟过程

本研究将入射粒子和靶核看作是点粒子，不考虑其体积。入射时假定每一个入射粒子都以固定的能量垂直射向靶核所在平面。考虑到靶核质量远大于入射粒子，散射过程中可以认为靶核位置固定。

模拟中，首先应进行初始化，设定散射过程中的几个参量，主要包括入射粒子能量、入射粒子初始坐标及靶核坐标。入射粒子的坐标与速度确定后，即可对一次散射进行模拟。模拟过程中，认为入射粒子只受库仑力作用。整个过程可以看作由若干微小时间间隔Δt 组成，每一段间隔内，粒子所受库仑力近似被认为不变。利用特定的算法得出微小时间间隔后入射粒子的速度与坐标。通过多次迭代运算即可得到此次散射过程的轨迹，最后求出该次散射的散射角。通过蒙特卡罗方法随机给定多个粒子的初始坐标，再利用上述方法模拟出每个粒子的散射轨迹及散射角。对大量粒子的结果进行统计后即可得到散射几率。

可以看出在上述模拟流程中，单次散射的轨迹算法对模拟效率起到了关键性作用。因此，下面对多种模拟算法进行详细的讨论和比较。

1.2 轨迹模拟算法

1.2.1 欧拉方法

欧拉方法即为文[8—9]中所使用的算法，是一种以迭代为基本思想的常微分方程的数值解法。

公式（1）给出了位置函数r 的Taylor 展开[10]，

其中r(t)是t 时刻α 粒子所在的位置，r(t+Δt)是t 时刻又经过一个微小时间段Δt 后α 粒子所在的位置。

取展开式的前两项，得到：

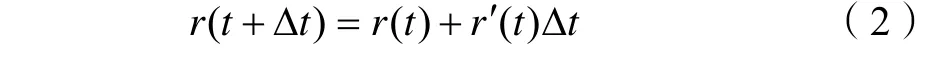
该公式说明仅需初始时刻的r(t)和t 时刻的r 的微分值（即速度v）即可近似得到t+Δt 时刻的r 值。该算法的误差为二阶。

显然，欧拉方法的误差较大，为满足模拟精度的要求，需要将步长Δt 取的较小，而Δt 过小又会导致模拟效率较低。因此在本研究中尝试使用其他的算法。

1.2.2 基本Verlet 算法

基本Verlet 算法是一种求解牛顿运动方程的数值方法，其作为一种积分方法，被广泛运用于分子动力学模拟、行星运动等领域。

对位置函数r 进行Taylor 展开：

可以看出，在该方法中，为了得到t+Δt 时刻的r值，需要t 及t-Δt 时刻的r 值以及t 时刻的加速度。该方法的误差为四阶[11]，精度要高于欧拉算法，但在计算过程中并没有显式求出速度，这给最终的散射角计算带来一定的困难。

1.2.3 Velocity Verlet 算法

在基本Verlet 算法的基础上，人们又发展出了Velocity Verlet 算法，该算法也有广泛的应用范围。

分别对t 和t+2Δt 时刻的位置函数r 进行Taylor展开并取前3 项：

可以看出该方法的误差同样为四阶[11-13]，与基本Verlet 算法完全一致，但该算法可以显式给出每一时刻的速度与位置。

1.2.4 算法比较

为了选择出最佳算法，本文比较了3 种算法的模拟精度及效率。图1 中的3 组图给出了1、5、10 MeV 3 种不同入射粒子能量下3 种算法的模拟误差。从图中可以看出：在3 种能量下，欧拉方法的误差都大于2 种Verlet 算法；随着入射粒子能量的增加，欧拉方法的误差变化没有固定规律，而2 种Verlet 算法误差则逐渐减小且算法误差基本一致。

图1 不同入射粒子能量下3 种算法误差比较

表1 给出了3 种算法运行万次的用时。可以看出：欧拉法与基本 Verlet 算法效率基本相同，Velocity Verlet 算法较另外2 种方法效率略有提高。表2 详细比较了3 种算法的异同。综合考虑这些因素可以得到：在轨迹模拟中，Velocity Verlet 算法较其他2 种算法误差更小，效率更高，也更加方便。因此，选定Velocity Verlet 算法作为改进后的模拟程序的轨迹算法。

表1 3 种算法模拟时间比较

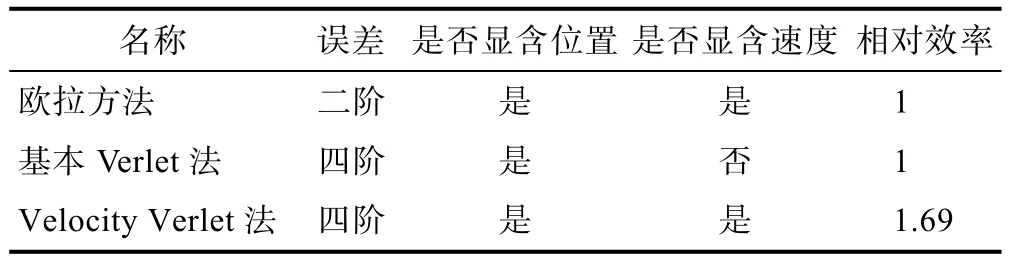
表2 3 种算法综合比较

1.3 变步长处理

确定好轨迹算法后，模拟效率得到了一定的提高，但还达不到要求。本文希望能进一步提高模拟效率。图2 给出了α 粒子散射过程中距靶平面不同距离时的受力情况。可以看出，α 粒子在大部分区间（距离靶核较远）内受到的库仑力很小，速度变化很小，因此模拟时步长Δt可以取的较大；而α 粒子距离靶核较近时，库仑力会急剧增大，该阶段对最终的散射轨迹影响很大，因此模拟计算的步长Δt需要取的相对较小，才能保证模拟精度。因此，步长Δt的大小与粒子所受的库仑力有关。

为了确定步长 Δt的具体形式，本研究采用了将粒子动量在每个模拟步内变化控制在一个固定值这一标准。而粒子动量在每个模拟步内变化即为其所受到的冲量。这样就可以根据公式（11）求出每一步的步长值。可以看出每一步的步长与粒子所受库仑力F成反比。

图2 散射过程中F-Z 变化曲线

λ为一固定冲量， 在本研究中其大小取为 6.64×10-23N·s。

对程序进行变步长优化后需要对其结果进行检验。而检验的标准即为变步长后的模拟精度是否仍在可接受范围内。图3 是对模拟程序进行变步长处理后，3 个入射粒子能量下散射角误差随瞄准距离的变化图。在3 种入射粒子能量下，散射角绝对误差全部都不超过1°，可以满足模拟要求。当入射能量较高，瞄准距离较短时，误差相对较大；其余情况下，误差都较小且比较稳定。

图3 变步长后不同入射能量下的误差

2 结果与分析

经过算法筛选、步长动态处理两方面的优化后，最终给出了基于变步长Velocity Verlet 算法的卢瑟福散射模拟程序。下面将其与原来基于定步长欧拉算法的卢瑟福散射模拟程序进行比较。

图4 是优化后程序与原程序的误差对比图。图4(b)给出了原程序的模拟误差，可以看出：不同入射能量下的绝对误差普遍小于0.9°；误差随瞄准距离的增大先迅速变大而后减小，在约200 fm 附近出现误差最大值。图4(a)给出了优化后程序的模拟误差，可以看出：不同入射能量下散射模拟的绝对误差同样都小于0.9°；误差随瞄准距离的变化与原程序基本一致，也是先迅速变大而后减小，在200 fm 附近出现最大值。两张图对比，可以得到：在较低入射能量下，优化程序精度与原程序基本一致；在较高入射能量下，优化程序的精度比原程序更好一些。

图4 优化程序、原程序误差比较

表3 给出了原程序和优化后的程序在不同入射能量下运行万次所需要的时间。可以看出，在同样条件下优化后的程序运行时间较原程序减小2 个数量级左右。随着入射能量的增加，原程序用时与优化后程序用时的比值基本保持不变，稳定在135 左右。

表3 优化前后万次运行平均用时

本文首先详细讨论比较了多种轨迹算法，并从中优选出了Velocity Verlet 算法；然后根据入射粒子的具体受力情况提出了变步长的模拟方法。通过两步优化可以使得卢瑟福模拟的效率得到大幅提高，优化后程序的万次运行平均用时可以下降到原程序的约1/135。