某中低速磁浮轨道巡检车动力学特性研究

朱震寰

(中国铁建重工集团股份有限公司 湖南长沙 410100)

1 前言

中低速磁浮由于其环境友好、选线灵活的优势在各种类型新型轨道交通中具有很强的优势，并持续获得越来越广泛的应用[1-2]。在中低速磁浮系统中，列车与轨道的匹配精度要求高，保证良好的轨道状态是保证行车舒适和安全的基础。在运营过程中轨道检测是保证安全运行的主要措施。

目前，在磁浮轨道巡检研究领域，邓赞[3]对磁浮维护牵引车车辆系统进行了动力学仿真。曾长操等[4]研究了高速磁浮轨道巡检车的侧向动力学性能和导向系统的安全性。张耿等[5]73建立了唐山低速磁浮试验线的轨道不平顺谱。德米特里·波戈列洛夫等[6]基于Universal Mechanism(UM)开发了磁浮列车-轨道梁耦合振动仿真的专用程序UM Maglev。陈琛等[7]采用虚拟激励法将轨道不平顺产生的随机激励转化为系统输入激励。Zhang等[8]研究了基于机器视觉检测技术的中低速磁浮F轨轨缝的动态检测方法。魏高恒等[9]分析了不同波长的轨道垂向激励对磁浮车辆系统动力学的影响。

CXJ-5磁浮智能巡检车是中国铁建重工集团股份有限公司针对中低速磁浮轨道线路智能巡检功能而开发的一种集人员输送及轨道检测于一体，具备高速巡检和低速精细检测模式的新型中低速磁浮轨道工程作业车。该车设计的高速走行速度为25 km/h、低速检测速度为5 km/h。为了提升磁浮智能巡检车运行速度，并保证其平稳性，增强其适用性，本论文通过建立动力学模型仿真以及工程试验验证来研究该车的动力学特性，并进行优化设计。

2 中低速磁浮轨道巡检车动力学模型

中国铁建重工集团股份有限公司研制的磁浮智能巡检车如图1所示。

该车主要由车体、底盘、检测小车及附件构成。根据巡检车的结构，巡检车的基本组成为:车体、车架、车桥、车轮，其中车体通过6个减振器与车架相连、车架通过4个橡胶减振组件与2个车桥相连、车轮与车轴可相对转动。车轮与轨道的相互作用力采用Pacejka轮胎模型表示，并将径向刚度提高，以模拟实心橡胶车轮与轨道的作用力。车架四周的4个导向装置采用车架与轨道间的弹簧模型模拟，整车模型拓扑图如图2所示。

图1 中低速磁浮智能巡检车

图2 中低速磁浮轨道巡检车动力学拓扑模型

图2中车体与车架采用xyz三自由度铰连接，车架与车桥采用xyz三自由度铰连接，车桥与车轮之间采用β转动自由度铰连接，车架与地面间采用syzφγψ六自由度铰连接，车架与车桥间橡胶衬套采用动刚度弹簧单元模拟，车体与车架间的减振器采用弹簧阻尼单元模拟，车轮与地面接触模型采用Pacejka轮胎力模型模拟，导向机构与轨道的导向力采用弹簧单元模拟。

2.1 主要计算参数(见表1)

表1 模型参数

2.2 轮胎模型

魔术公式是用三角函数的组合公式拟合轮胎试验数据，用一套形式相同的公式表达轮胎的纵向力Fx、侧向力Fy、回正力矩Mz、翻转力矩Mx、阻力矩My以及纵向力、侧向力的联合作用工况。

魔术公式的一般表达式为:

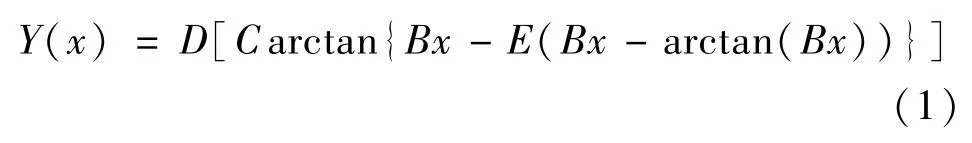
式中，Y(x)可以是侧向力、回正力矩或者纵向力，自变量x可以在不同的情况下分别表示轮胎的侧偏角或纵向滑移率，式中的系数B、C、D依次由轮胎的垂直载荷和外倾角来确定。

本文基于车轮静载试验数据以及文献[10-12]，选择较大的径向刚度数值和较小的轴向刚度数值，设定车轮参数如表2所示。

表2 车轮参数 N/m

2.3 轨道激励

中低速磁浮轨道主要由F轨、轨枕、减振元件、接头等构成，由于结构与铁路不同，现有的轨道谱不适合作为磁浮轨道上走行的车辆仿真使用。本文基于张耿等[5]76的研究，设定轨道谱如图3所示，波长范围设为0.3～16 m。

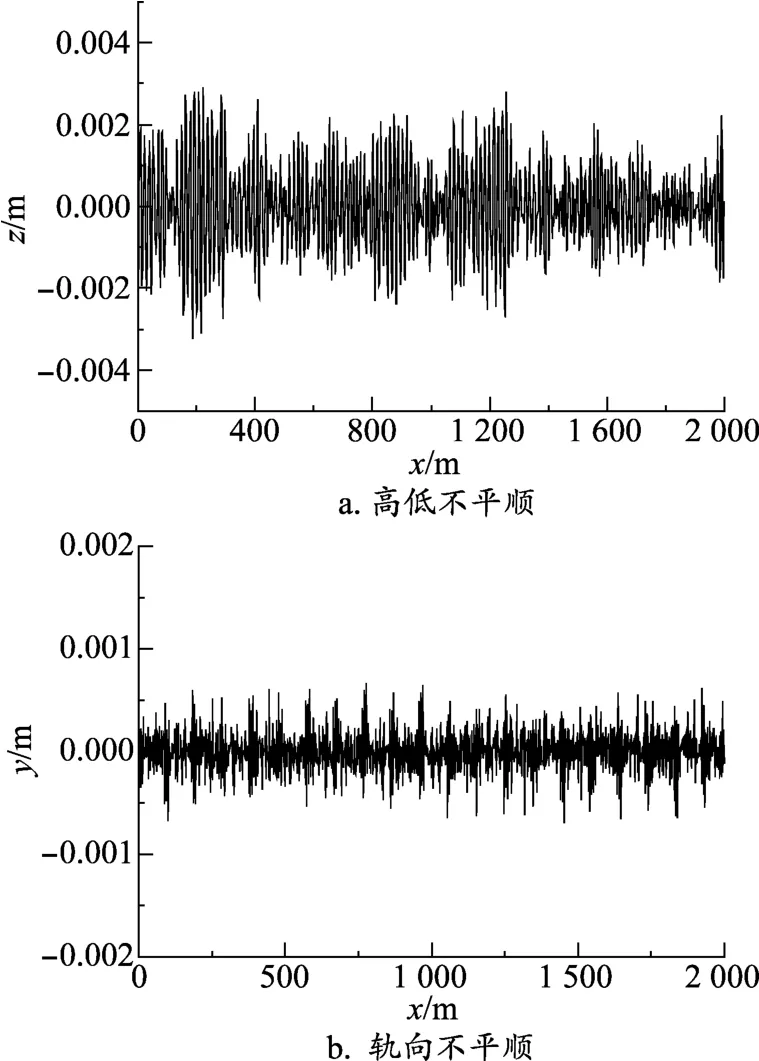
图3 轨道不平顺谱(时域)

3 工程试验概述

在某磁浮试验线上进行工程试验，试验速度20 km/h，直线段距离为2.2 km的线路进行匀速走行。在座椅安装座处布置加速度传感器(美国LORD无线加速度传感器G-LINK-200)。设定采样频率为256 Hz。将加速度传感器安装使得Z轴设为竖直方向、X轴设为车辆前进方向，Y轴设为车辆的横向。

4 结果及讨论

4.1 垂向加速度

如图4所示，图4a为动力学仿真所得的车体座椅处垂向加速度的仿真值，图4b为加速度的频谱分析图。

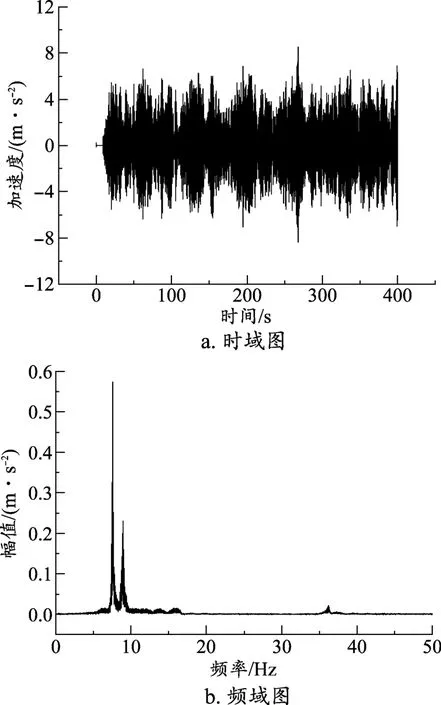
图4 车体垂向加速度仿真值

如图5所示，图5a为在线路上试验所测量得到的车体座椅处垂向加速度的实测值，图5b为加速度的频谱分析图。

对比图4与图5，车体的垂向加速度仿真所得最小为-8 m/s2、最大为8 m/s2，实测所得最大值为8 m/s2，最小值为-14 m/s2。在频谱图中仿真模型的垂向振动能量集中在9 Hz、36 Hz等频率上，实测的垂向振动能量集中在3 Hz、9 Hz、35 Hz等频率上。这表明本文所建立的磁浮智能巡检车的动力学模型可以基本反映垂向振动幅度。不足之处在于振动能量频率来源不够完全，这是因为轨道不平顺所含的频率种类不够，比如实际的磁悬浮轨道的随机不平顺功率谱具有分段特征[13]，本论文采用的不平顺谱不完全反映实际磁浮轨道不平顺特征[5]76。具体分析梁自身的频率成分[14-15]包括一阶竖向频率5.365 Hz、二阶竖向频率8.950 Hz、三阶竖向频率9.859 Hz，其中的二阶、三阶频率也是车体振动的主频率，因此论文所建模型可以反映车辆运行过程中的车体振动特性。

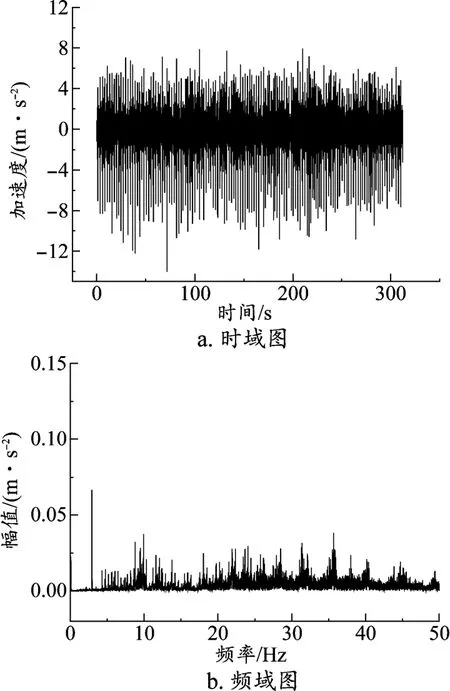
图5 车体垂向加速度实测值

分析垂向振动的频谱发现，车辆在8～10 Hz的区域内，振动能量大。而二系的固有频率为:

式中，ξ为阻尼系数，k为刚度，m为簧上质量。

计算得f＝9.4 Hz，与图4中的垂向振动频谱特性的能量最大处一致，因此，车体的垂向振动能量主要来源于二系固有振动能量，可以认为垂向振动偏大的问题是二系刚度与轨道激励的频率不匹配所致。

4.2 车体横向加速度

如图6所示，图6a为动力学仿真所得的车体座椅处横向加速度的仿真值，图6b为加速度的频谱分析图。

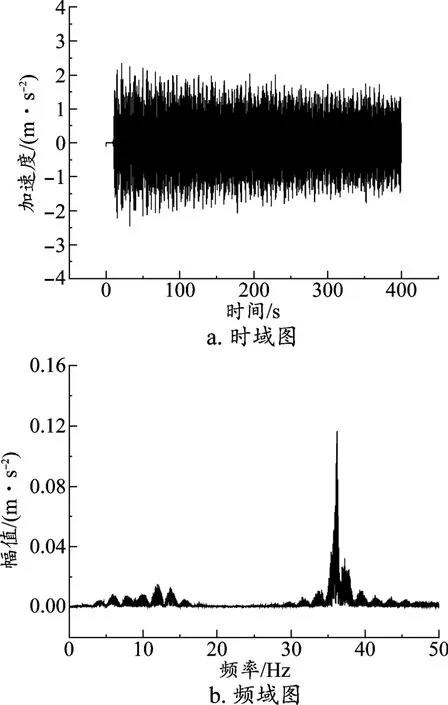
图6 车体横向加速度仿真值

如图7所示，图7a为在线路上试验所测量得到的车体座椅处横向加速度的实测值，图7b为加速度的频谱分析图。

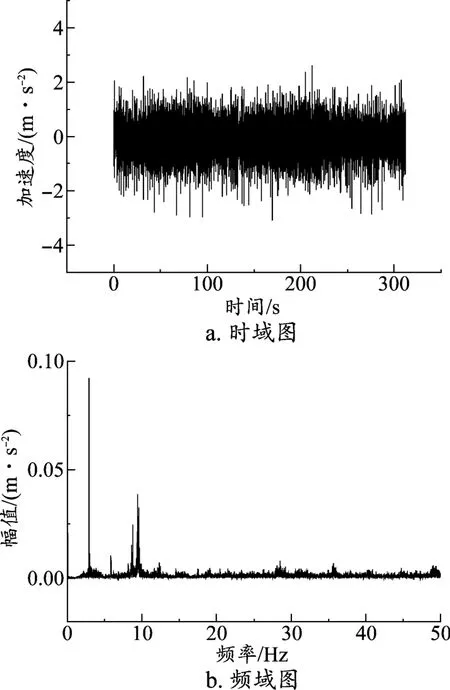
图7 车体横向加速度实测值

对比时域图，车体横向加速度的仿真所得最小值为-2.4 m/s2，最大值为2.3 m/s2，实测所得最小值为-3 m/s2，最大值为2.3 m/s2。

对比频域图，仿真所得的横向振动在频率为12、14、36 Hz处具有较大能量，实测所得的横向振动在频率2、9、29、36 Hz等处具有较大能量。

根据垂向加速度、横向加速度的仿真值与实测值比较分析，仿真结果与实测结果接近，因此本文建立的动力学模型可以反映磁浮轨道巡检车的垂向振动以及横向振动特性，可以基于该模型进一步研究整车的动力学特性。

4.3 车辆平稳性改进

磁浮轨道巡检车的高速巡检功能需要尽可能高的巡检速度，以利于减少巡检时间，提高轨道检测效率。而在工程试验中发现，车辆的速度在超过20 km/h时，振动显著变大，平稳性变差。论文分析了不同车速下的垂向平稳性指标，车辆在20～22 km/h以及15 km/h以下条件下运行垂向平稳性指标小于3，较为平稳，而超过20 km/h时，速度越快平稳性越差，最高运行速度在25 km/h以下。

为了改善该问题，提高车辆的平稳性，基于4.2节分析，本文采用改变二系刚度选调节二系的固有频率的方法，避免车体振动与轨道激励的频率重叠，改善车体的振动。在比选市场常用减振器的基础上，作者选择了某二系的减振器，其垂向刚度为270 000 N/m。

分别以不同的速度对磁浮智能巡检车整车进行动力学仿真，依据GB/T 17426标准对车体座椅处的垂向振动加速度值进行处理，分析整车的平稳性指标。将原减振器参数与改进选型后的减振器参数的计算结果进行对比，得到垂向平稳性指标进行如图8所示。

图8 垂向平稳性指标与速度关系

由图8可见，改善前车辆速度小于25 km/h时，平稳性指标在3.5～4以内，达到货车平稳性良好的要求；在车辆速度25～35 km/h范围内，平稳性指标在4～4.25以内，达到货车平稳性合格要求；在超过35 km/h以后，平稳性指标不合格。

减振器选型改进后，车辆在0～35 km/h的速度区间垂向平稳性指标均小于等于3.5，可达到货车平稳性优的指标。而在35～45 km/h的速度区间平稳性指标在3.5～4以内，达到货车平稳性良好的要求。相较现有车辆相比可以显著改善其平稳性，因此选型是合适的。

5 结论

(1)本文建立的磁浮智能巡检车的动力学模型的仿真结果与实测结果的时域特性与频域基本一致，证明了动力学模型的有效性。

(2)仿真发现当前车辆配置条件下车辆速度超过25 km/h时垂向平稳性变差。

(3)通过优化车架与车体间减振器参数，进行动力学仿真，结果表明新的减振器参数对车辆垂向平稳性有较大改善，可用于后期中低速磁浮轨道巡检车改进。