大粒径石块分布对土石混合体稳定性的影响

杨小彬， 侯 鑫， 裴艳宇， 阚李浩， 吕祥锋

(1.中国矿业大学(北京) 应急管理与安全工程学院， 北京 100083； 2.北京科技大学土木与资源工程学院， 北京 100083)

土石混合体是指形成于第四纪，由一定强度的石块和土体组成的特殊工程地质材料。土石混合体中石块和土体的不同性质、石块形状、大小、数量、分布方位等因素导致其在结构上表现出强烈的非均匀性。正是由于这种不连续、非均匀的结构特性，使其在实际工程应用和试验研究中呈现出一种既不同于土体又不同于岩石非土非石的力学性质[1-3]。

广大学者对土石混合体物理力学性质、破坏变形等方面开展了大量研究，主要研究方法有现场原位试验、室内试验和数值模拟。现场原位试验方面，李晓等[4]、油新华等[5]、徐文杰等[6]通过对土石混合体进行大型野外原位推剪和压剪试验，得出了土石混合体在天然状态下的全应力-应变曲线及其相应的抗剪强度参数。在室内试验方面，邓华锋等[7]通过现场采集试样，进行了不同含水率的土石混合体大试样室内直剪试验，提出了用临塑抗剪强度和极限抗剪强度来分析土石混合体的抗剪强度的方法。夏加国等[8]利用大型三轴剪切试验仪，对含有超径颗粒的土石混合体进行了固结不排水剪切试验，分析了其在不排水剪切情况下的体积变化规律。在数值模拟方面，数值试验的首要前提是建立符合土石混合体真实情况的物理模型。目前土石混合体模型的生成方法主要有两种：①基于蒙特卡洛计算方法的随机生成土石混合体模型[9-10]；②运用数字图像处理技术直接生成土石混合体模型[11-12]。严颖等[13]采用球体单元模拟土颗粒，通过组合颗粒单元构造非规则形态的石块，对不同含石量和石块空间分布下土石混合体的直剪过程进行了离散元数值模拟。丁秀丽等[14]通过建立非饱和土石混合体的细观数值模拟方法，分析了土-石界面接触特性、含石量及饱和度等因素对非饱和土石混合体力学特性与破坏机制的影响。

石块作为土石混合体中重要的物质组成成分，在土石混合体中承担着骨架作用，而大粒径石块又在整体石块中起着主要承载作用。因此，探究大粒径石块对土石混合体稳定性的影响，对于工程应用中人造土石混合体边坡稳定性研究具有一定的参考价值。故此基于图像处理技术构建接近真实情况的土石混合体模型，利用ABAQUS有限元分析软件探究大粒径石块的不同分布位置和角度对土石混合体稳定性的影响。

1 土石混合体模拟方法

1.1 土石混合体物理模型的建立

以平朔东露天矿实地调查情况为基础，矿区中的土石混合体广泛存在于天然土坡和抛填块石土堆中，土体和石块分选性较差，石块粒径大小不一，土-石之间存在不同程度的胶结情况，现场调查某一土石混合体边坡如图1所示。

图1 土石混合体边坡Fig.1 Soil-rock mixture slope

由于土石混合体中土体和石块颜色差异较小，直接利用图像处理技术无法较为准确地提取石块边缘信息。针对这种情况，采取先通过图像处理软件将石块从土石混合体中剥离，再对其边缘进行提取的方法，较好地保留了模型的真实性。通过图像处理技术构建土石混合体物理模型流程如下：

(1)图像获取。选取土体和石块分选较为明显的区域进行拍照，尽可能减少外界因素对图像后期处理的影响。

(2)图像预处理。将所获取图像导入Photoshop软件中转化为灰度图像，并对图像进行一系列的优化、去噪，最后对模型中石块进行土石分隔。

(3)提取图像边缘。将分隔后的石块图像在Photoshop中进行边缘提取。随后把所提取边缘图片导入Illustrator中，将所提取石块边缘转化为可编辑的矢量图。

(4)图像边缘调整。将(3)中所得的石块边缘矢量图导入Auto CAD中对其边缘进行处理，统计各石块面积，并对一些不理想的区域进行微调。

处理前后模型如图2所示。

图2 土石混合体模型示意图Fig.2 Schematic diagram of soil-rock mixture model

1.2 土石混合体模型参数

模型尺寸为700 mm×1 100 mm，采用摩尔-库伦破坏准则，在模型上部边界施加位移载荷，模型轴向应变达到5%时计算停止。模型底部边界为固定边界，两侧为自由边界，同时将模型简化成平面应变问题。采用非对称算法对其进行计算，选用非关联流动法则，即(剪胀角ψ不等于内摩擦角φ)。本文根据赵星光等[15]、孔位学等[16]对岩土工程中剪胀角参数的研究，选取剪胀角为内摩擦角的1/2。土石混合体中土体和石块的物理力学参数如表1所示。

表1 土-石参数Table 1 Soil and rock parameters

1.3 土石混合体数值试验方案

为探究大粒径石块对土石混合体的影响，对所建立的土石混合体模型中各石块面积进行统计，选取15块面积最大的石块作为此次试验的研究对象。对模型中大粒径石块的分布位置和角度进行调整，在所建立的土石混合体原位模型的基础上，分别建立针对不同情况的土石混合体模型，分2组进行数值试验。

(1)通过MATLAB中随机函数在模型指定区域生成随机坐标，将模型中大粒径石块和其余石块分别随机分配到模型的上部和下部两个区域，分配后模型如图3所示。

图3 大粒径石块不同分布位置模型Fig.3 Models of different distribution locations of big stones

(2)在Auto CAD中将模型中大粒径石块距离最远的两点连线作为石块的长轴，定义石块长轴与模型底部边界平行时为0°。为了减小其他石块对模拟结果的影响，对于大粒径石块转动而引起的石块边界相交的情况，选择删除相交石块中面积较小的石块。依次将大粒径石块长轴倾角调整为0°、30°、45°、60°、90°，调整后模型如图4所示。

2 结果分析

2.1 大粒径石块位置对土石混合体稳定性的影响

图5为大粒径石块在模型中不同分布位置时的应力-应变曲线。试验模拟了在单轴压缩情况下土石混合体的力学响应。从图5中可以看出土石混合体的单轴压缩过程总体可以分为3个阶段：①土石混合体在初步受压时，内部土体受压变形，裂隙逐渐压缩闭合的线弹性阶段；②曲线偏离线性，试件内部随着应力增大，微裂隙数量逐渐增多的塑性破坏阶段；③应力达到土石混合体最大承载能力后，试件表现出一定的应变硬化或软化特征，此后强度不再降低，应变却不断增大的残余强度阶段。

如图5所示，在模型达到同等应变情况下，大粒径石块在上部区域时所对应的应力最大；在模型中自然分布时，次之；在下部区域时，最小；所对应的峰值强度同样符合这一情况。当大粒径石块在模型上部区域和在模型中自然分布时，土石混合体应力-应变曲线的峰后阶段表现出一定的应变软化特征。而当其位于下部区域时，峰后表现出一定的应变硬化特征。

图4 大粒径石块不同角度模型Fig.4 Models of different angle of big stones

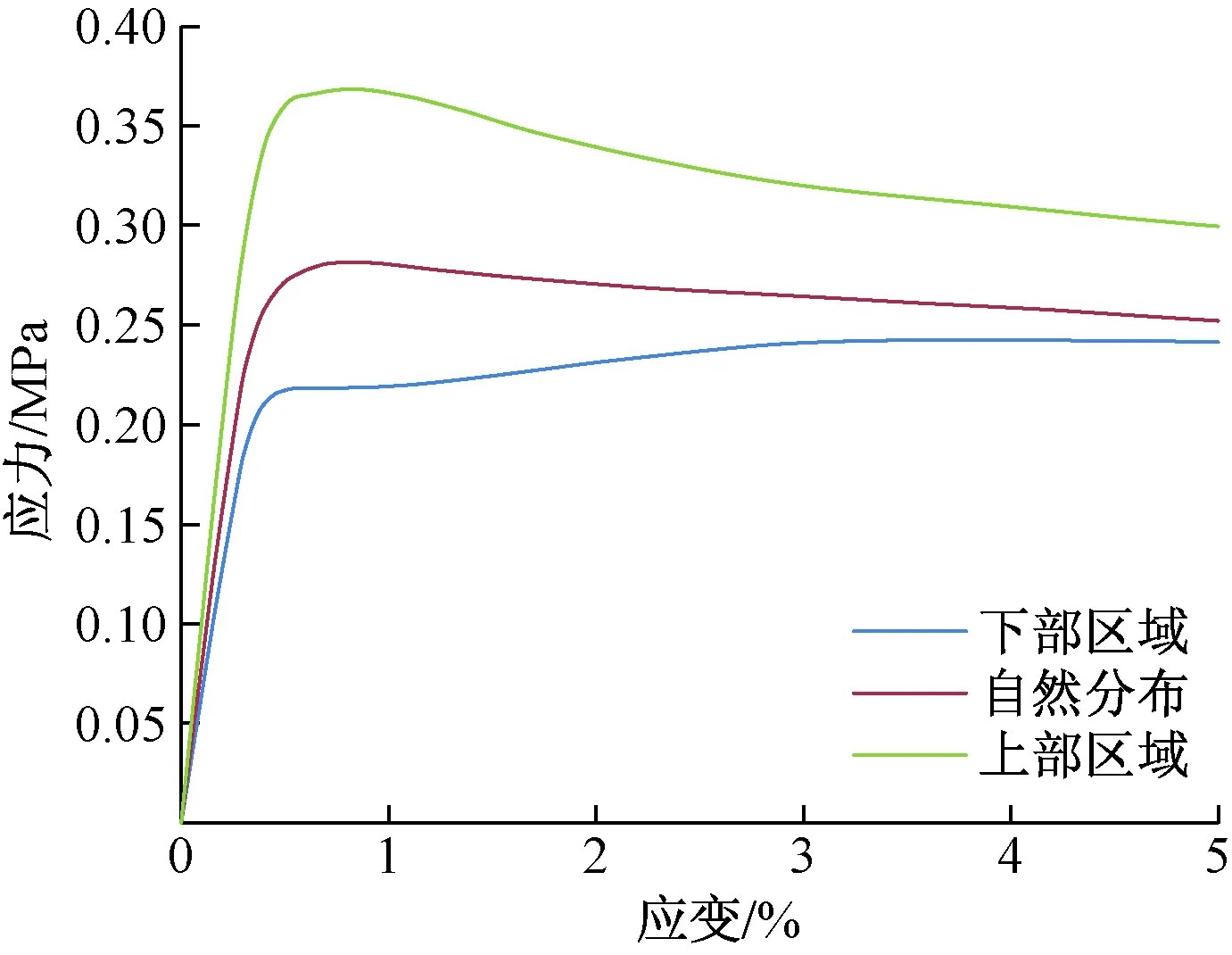
图5 大粒径石块不同位置土石混合体应力-应变曲线Fig.5 Stress-strain curve of soil-rock mixture at different locations of big stones

图6为大粒径石块处于不同分布位置时所对应的应力-应变曲线峰值时间节点和模型完全破坏时的塑性区发展云图。从图6可以看到，大粒径石块的分布位置对模型塑形区发展有一定的影响。如图6(a)所示，当大粒径石块位于上部区域时，塑性区主要分布在模型的下半部分，同时土石混合体的侧向鼓胀现象也表现于模型下半部分。这是由于下部区域分布多为小粒径石块，其区域强度低于上部区域。当模型初步受压时，上部区域的大粒径石块对于应力在模型中的传递存在较好的阻碍作用，表现为整体模型的抗压强度较大，稳定性较好。当模型继续受压至破坏时，塑性区由模型下半部分逐渐向上半部分扩展，最终形成贯穿整个模型的塑性区。在土石混合体原位模型中，塑性区首先出现在模型中部石块含量较少区域，随着加载过程进行，塑性区由中部向四周呈交叉分叉状传播，如图6(b)所示。

图6 大粒径石块不同位置土石混合体塑性区破坏云图Fig.6 Damage of plastic zone of soil-rock mixture at different locations of big stones

而在图6(c)中，大粒径石块位于下部区域时塑性区发展情况与位于上部区域时相反，大粒径石块聚集区域基本无塑性区。模型上部区域多为小粒径石块，局部承载能力较低，导致土石混合体强度相比于前两种情况较小，稳定性较差。由于模型底部保持了较好的完整性，在上部区域发生塑性破坏之后，试件承载能力主要由下部大粒径石块所集中区域承担，此时模型强度有所增大，从而使整体模型在峰后表现出一定的应变硬化特征。从图6中各塑性区发展情况可以看出，在土石混合体塑性区发展过程中，其发展形式可分为以下情况：塑性区沿石块边缘或绕过石块发展；塑性区在石块处分流发展，或者先分流绕过石块后再汇合发展。这与文献[17-18]中对塑性区扩展模式的描述基本一致。

2.2 大粒径石块角度对土石混合体稳定性的影响

为分析大粒径石块角度对土石混合体稳定性的影响，分别选取大粒径石块角度为0°、30°、45°、60°、90°时的5组模型作为研究对象。图7、图8分别为各试样在单轴试验情况下的应力-应变曲线和大粒径石块长轴不同倾角所对应的土石混合体峰值强度。可知，大粒径石块长轴倾角为0°和90°时，土石混合体峰值强度较大，其中0°时相较于90°时大；长轴倾角30°时，次之；长轴倾角45°、60°时，峰值强度较小。大粒径石块长轴水平或竖直放置时，对于应力在土石混合体模型中的传播以及塑性区发展有较好的阻碍作用，这种阻碍作用引起土石混合体局部区域产生较大的应力集中现象，表现为模型应力-应变曲线峰值强度较大。大粒径石块长轴与主应力轴斜交时，相较于前者，在试验过程中，塑性区多沿着石块表面发展，石块对于应力传播的阻碍作用降低，土石混合体稳定性较差，峰值强度降低。由图8中拟合曲线所示，土石混合体峰值强度随大粒径石块长轴倾角变化呈先减小后增大趋势发展。大粒径石块长轴倾角在45°～60°时，强度取得最小值。这与摩尔-库伦准则中所描述的，剪切滑移面与最大主应力作用面夹角为45°+φ/2=55°(φ为土石混合体中土体内摩擦角)基本一致。

图7 大粒径石块不同角度时土石混合体应力-应变曲线Fig.7 Stress-strain curve of soil-rock mixture at different angles of big stones

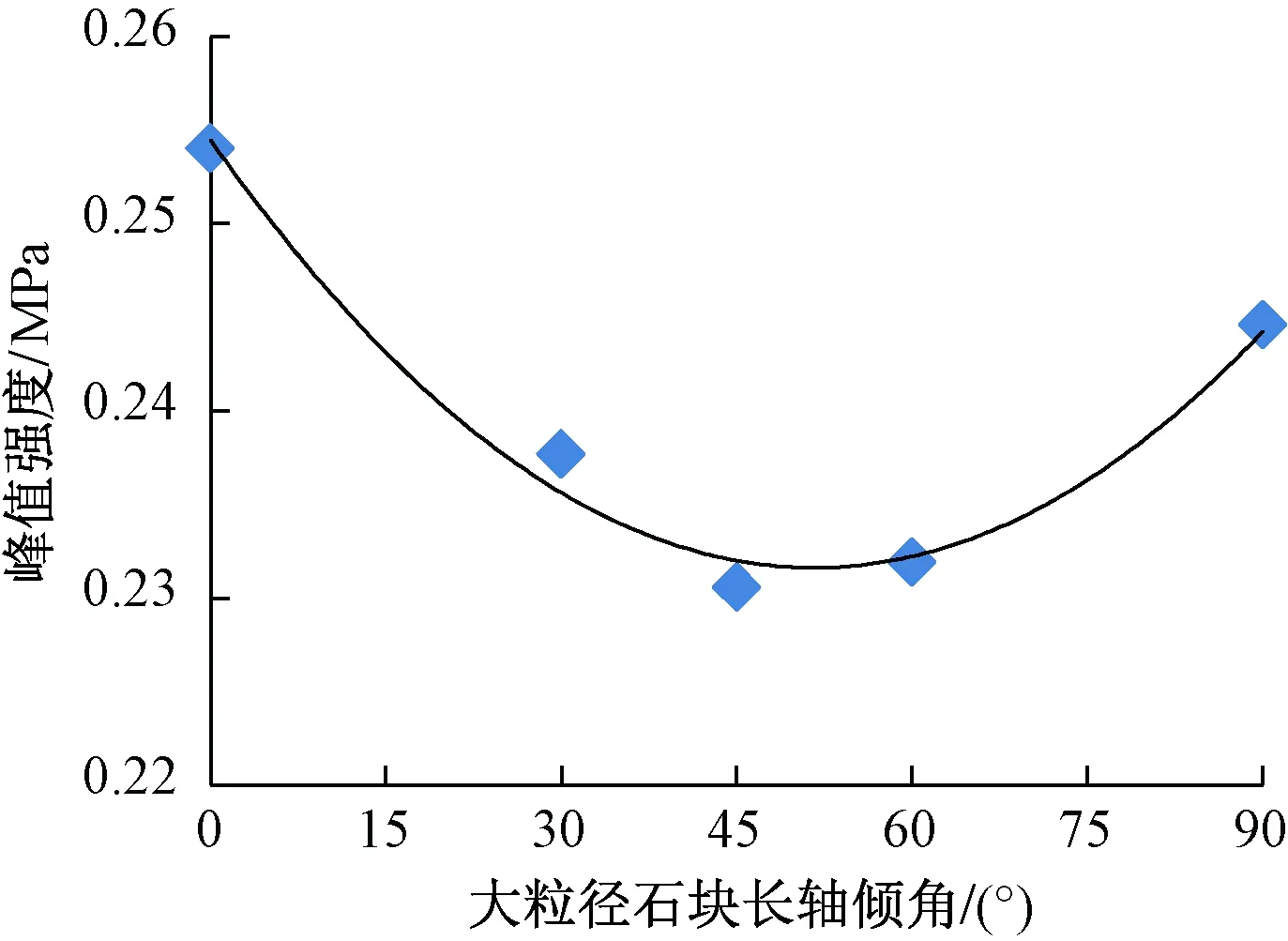
图8 土石混合体峰值强度随大粒径石块长轴倾角变化规律Fig.8 The variation of peak strength of soil-rock mixture with long axis angle of big stones

3 结论

针对大粒径石块处于不同位置和角度的土石混合体进行单轴试验，得到以下结论。

(1)大粒径石块集中分布在模型上部区域时，土石混合体强度最大；在模型中自然分布时，强度次之；在模型下部区域时，强度最小。

(2)大粒径石块对塑性区发展有一定的阻碍作用。大粒径石块在模型上部区域时，塑性区主要分布在模型下半部分，此时模型整体稳定性较高；大粒径石块在模型下部区域时，情况相反，模型整体稳定性较低。

(3)土石混合体强度随大粒径石块倾角增大呈现出先减小后增大的趋势。大粒径石块倾角在45°～60°，即摩尔-库伦破坏准则中剪切破坏面与最大主应力作用面夹角为45°+φ/2时，土石混合体强度取得最小值。