基于R/S分析及极限学习机的沉陷区土地复垦适宜性研究
陈 强,黄 鑫,拉换才让
(青海省水文地质及地热地质重点实验室/青海省水文地质工程地质环境地质调查院,西宁 810008)
随着采煤沉陷问题的日益严重,加之中国人口现状及有效耕地的不断缩减,使得土地复垦工作也越来越被重视。中国已于20世纪80—90年代开展了土地复垦研究,并取得了良好的效益和经验[1]。同时,在土地复垦研究方面,许多学者也取得了较好的成果,如肖武等[2]在分析地面地形特征的前提下,模拟了采煤的动态沉陷过程,并比较了不同阶段的复垦耕地率,从定量角度揭示了复垦耕地面积与沉陷积水面积间的关系;周宁等[3]基于草原矿区的实际情况,采用层次分析法构建了研究区的土地复垦适宜性评价模型,具有一定的借鉴意义;王锐等[4]在分析矿区土地退化的基础上,结合土地破坏现状和自然地理条件,提出了综合治理措施,为矿区的土地复垦工作提供了理论指导。上述研究虽从多方面研究了沉陷区的土地复垦,但忽视了复垦前采煤沉陷区稳定性的评价工作,且该工作对土地复垦至关重要,主要表现为若在沉陷区稳定前进行土地复垦,则复垦工程往往会因后期沉陷遭到破坏;若在稳定较长时间后才进行复垦,则会降低土地的有效利用率。因此,对沉陷区的变形稳定性评价就显得格外重要,也有不少学者在该方面进行了研究,如贾新果[5]对非充分开采条件下的沉陷规律进行了研究,得出沉陷变形值、沉陷范围及移动角之间的相互关系,为指导后期煤矿开采提供了依据;张子月等[6]通过构建沉陷区的动态沉降预测模型,有效掌握了沉陷变形与时间的关系,对矿区土地的持续生产具有重要的意义;赵忠明等[7]结合概率积分法、灰色理论和神经网络构建了沉陷特征参数的预测模型,经实例检验,该模型的预测精度较高,适用性较强。上述成果研究了多种预测模型在采煤沉陷预测中的适用性,但缺少土地复垦方面研究,也未涉及R/S分析及极限学习机的应用研究,存在一定的不足。因此,本研究以三河尖煤矿沉陷区为工程背景,先利用R/S分析判断沉陷区的稳定性现状,再利用极限学习机构建其变形预测模型,两者综合判断沉陷区开展土地复垦的适宜性;最后,结合区内工程实际,开展相应土地复垦措施研究,以便更好地指导后期施工。
1 基本原理
本研究分析过程主要包括2个阶段:阶段一,利用R/S分析及极限学习机分别构建沉陷区地表变形的趋势判断及预测模型,以综合评价地表变形的稳定性及发展趋势,进而为后续土地复垦奠定基础;阶段二,若前述判断沉陷区地表变形趋于稳定,则对沉陷区的土地复垦进行研究,以便更好地指导后期农业生产。
1.1 数据预处理
根据沉陷区地表监测的实际情况,监测数据往往具有非等距特征,且监测样本数偏少,不利于后续分析。为克服该问题,提出利用MATLAB软件的cftool工具箱实现沉陷变形与时间的分段线性插值,并根据后续分析模型的需求,将实测时间范围等分为若干区间,并求得相应时间节点处的沉陷值,以达到增加样本数的目的,并实现非等距向等距转变的处理。
1.2 稳定性评价模型的构建
R/S分析是分形理论的一种定量计算方法,能描述变形序列长期记忆性及稳定性,适用于地表变形的稳定性评价[8-11]。若将地表沉陷变形序列表示为{Ni},并将其分解为A个子序列,每个子序列长度为n,则子序列的平均值(ea)可表示为:

式中,Nk,a为第k个子序列中的第a个元素。
同时,计算各子序列的累计离差,并根据其最大值、最小值确定各子序列的极差(Ra)。
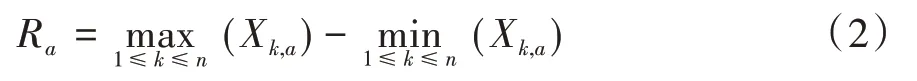
再计算各子序列的标准差(Sa)。

最后,将各子序列的重标极差(R/S)a表示为:

在不同n值情况下,可得到相应的(R/S)n,进而得到若干散点[n,(R/S)n],由于lgn与lg(R/S)n之间存在线性关系,即:

式中,C为待拟合常数,H为Hurst指数。利用Hurst指数实现沉陷变形的趋势判断及稳定性分析,其判断依据主要是:当0<H<0.5时,说明沉陷变形稳定性具有反持续性,即沉陷变形处于不稳定状态,且其偏离0.5越大,稳定性越差;当H越接近0.5,说明沉陷变形具有较强的游离性和随机性;当H>0.5时,说明沉陷变形具有持续稳定性,即沉陷变形处于稳定状态,且其偏离0.5越大,趋势性越好。
在结果的分析过程中,引入关联维数(D)和相关性度量参数(CM),前者可评价序列节点间的关联性,其值越大说明各节点的关联性越大,其值越小则节点间的关联性越小;后者可评价序列的相关性,其绝对值越大,说明相关性越强,反之相关性越弱,且C M为正值时,为正相关,反之为负相关。

1.3 变形预测模型的构建
上述R/S分析已判断沉陷区稳定性趋势,其判断为现有状态判断,然后再以极限学习机为基础,构建地表沉陷预测模型,以判断地表变形的发展趋势。
极限学习机(Extreme learning machine,ELM)是一种新型智能神经网络,优点为操作简单、运算速度快等。地表沉陷变形样本为(xi,yi),其对应预测值O j可表示为:

式中,g(x)为激励函数;M为隐层节点数;βi、wi为权值向量;b i为阈值。
根据预测思路,预测结果应零误差逼近实测值,则:

上式的矩阵形式如下:

式中,H为常数矩阵。
为实现零误差逼近预测,则需对上式进行最小二乘求解。
ELM模型虽属智能预测模型,但也存在一定不足:①ELM模型的常用激励函数有3种类型,即Sigmiod型、Sine型和Hardlim型,三者的应用多依据使用者经验而定,无法保证其最优性。②在ELM模型应用过程中需设定隐层节点数,故无法保证该参数的客观性。③ELM模型应用过程中的连接权值和阈值是随机产生的,随机性较强,仍待优化研究。
为保证地表沉陷预测精度,对上述3个不足均进行优化研究。
第一,鉴于激励函数类型相对较少,提出利用试错法对3种激励函数的预测效果进行对比分析,进而确定出最优激励函数。
第二,ELM模型属神经网络模型,根据神经网络模型隐层节点数的经验公式初步计算得到初始隐层节点数,再以该节点数为中心,扩展隐层节点数范围,并对范围内的隐层节点数进行试算,以确定出最优隐层节点数。隐层节点数(M)的计算公式:

式中,m、n分别为输入、输出层节点数;z为调节常数,一般取10。
由于m=6、n=1,则初始隐层节点数为13,故将试算区间设定为10~16。
第三,由于连接权值和阈值具有随机性,无法通过试算求得,且鉴于粒子群算法的全局优化能力,进而利用粒子群算法优化ELM模型的连接权值和阈值。优化过程:①参数初始化。将粒子群规模设置为400,粒子维数设置为2,分别代表连接权值和阈值,最大迭代次数为350,其他参数随机设置。②迭代寻优。在迭代过程中,将预测误差平均值作为适宜度值,不断对比粒子适宜度值与全局最优适宜度值,若粒子适宜度值更优,则将其替代全局最优适宜度值,反之,继续迭代寻优。③输出结果。当达到最大迭代次数后,输出全局最优适宜度值条件下的连接权值和阈值,进而实现二者的优化。
结合上述优化方法,将优化过程设定为:先利用经验公式计算出初始隐层节点数,对3种激励函数进行寻优;在确定最优激励函数前提下,计算不同隐层节点数的预测效果,进而确定最优隐层节点数;最后,利用粒子群算法实现连接权值和阈值的优化预测。
2 实例分析
2.1 工程概况
三河尖煤矿位于江苏省徐州市沛县龙固镇境内,交通较为便利,属黄淮冲积平原地貌,地形起伏较小,地势较为平坦,略向东北倾斜。区内下覆基岩以泥岩、砂岩为主,平均厚度约661 m,并夹有一定的石灰岩;上覆土体平均厚度220 m,由东向西不断增厚。同时,矿区下覆可采煤层主要为山西组7、9煤和太原组17、21煤,总厚度平均为9.73 m,且于2000年9月开采至今,共开采31个工作面,平均采深700 m。采煤方法为走向长壁法,顶板管理方法为全部冒落法。另外,随着工作面的开采,地表沉陷日益严重,为及时掌握地表沉陷规律,建立了地表移动观测站,获得了大量的地表沉陷实测数据,其中,L45监测点的实测结果如表1所示。
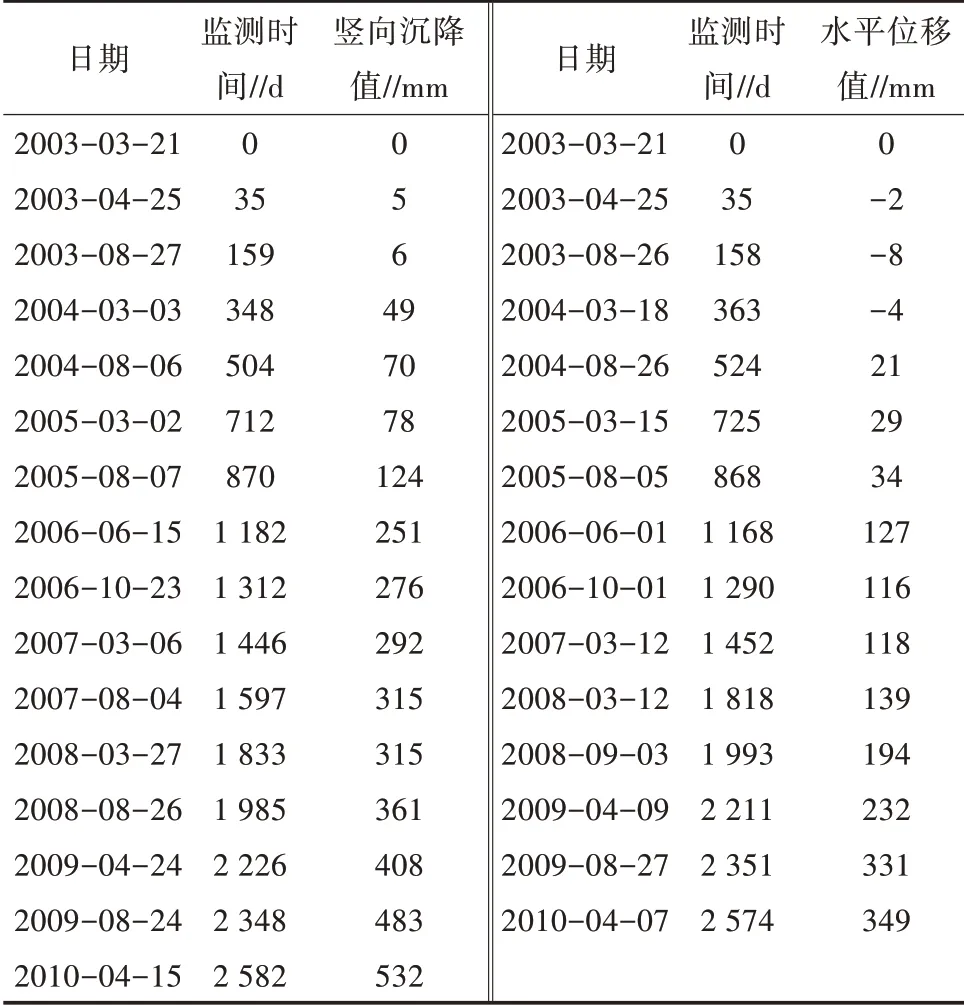
表1 L45监测点沉陷实测数据
根据L45监测点竖向沉降和水平位移的监测结果,得出该点的沉陷变形具有非等距特征,需进行数据处理。因此,通过线性插值处理,得到L45监测点处理后的沉陷曲线如图1所示。结合R/S分析的基本原理,将2个变形序列等分为60个周期,其中竖向沉降序列是43.76 d/周期,水平位移序列是43.63 d/周期。

图1 L45数据处理后的变形曲线
2.2 沉陷稳定性分析
2.2.1 整体稳定性分析 为充分评价沉陷变形的稳定性,将沉陷区的累计变形序列与速率序列均进行R/S分析,结果如表2所示。由表2可知,沉降变形和水平变形各序列的Hurst指数均大于0.5,说明各序列具有长期记忆性,沉陷变形处于稳定状态,且速率序列较变形序列的Hurst指数小,说明前者的稳定性判断趋于保守,后者稳定性评价更高;在关联维数评价中,以速率序列的关联维数相对更大,说明速率序列节点间的关联性相对更强;相关性度量参数CM均大于0,说明各序列的相关性均为正相关,且以变形序列的相关性相对更强;各序列的拟合度均趋近于1,说明各序列的拟合效果均较好。

表2 沉陷变形稳定性分析
变形序列的自相关性会放大分析结果的显著性,减弱分析结果的可信度[8]。因此,进一步采用AR(1)模型对各沉陷变形序列进行去相关性处理,并重新进行R/S分析,结果如表3所示。对比表2和表3,得出各序列在去相关性处理后,Hurst指数和C M指标均出现不同程度的减小,但关联维数D和拟合度却有不同程度的增加,说明AR(1)模型能很好地去除变形序列的自相关性,且在去除相关性后会减小沉陷变形的稳定性趋势,但会增加各序列节点间的关联性,并提高拟合精度。值得指出的是,通过去相关性处理后,沉陷变形的稳定性现状评价结果并未改变,仍处于稳定状态。

表3 去相关性后的沉陷变形稳定性分析
2.2.2 分阶段稳定性分析 为进一步分析沉陷变形稳定性随时间的演变规律,再采用递增时段和等时段的分阶段方式对沉陷变形的稳定性进行评价。
1)递增时段分析。递增时段分析是先选取监测前期若干序列进行R/S分析,再依次递加分析序列,得到相应各递增阶段的Hurst指数,计算结果如表4所示。由表4可知,竖向沉降序列和水平位移序列的前期Hurst指数均较小,且随分析序列的不断叠加,Hurst指数逐步增加,说明随时间的持续,沉陷变形趋于稳定,且2个序列的分析结果具有较好的一致性,验证了R/S分析的有效性;同时,递增各阶段的拟合度均较高,说明拟合效果较好,所得Hurst参数的可信度较高。

表4 递增时段稳定性分析
2)等时段分析。等时段分析是将监测周期等分为若干区间,对各区间进行相应的R/S分析,相关计算结果如表5所示。由表5可知,两序列在不同时段的Hurst指数均有所差异,且随时间持续不断增加,说明沉陷稳定性随时间是变化的,体现了分阶段分析的必要性,并在相应阶段,竖向沉降序列的Hurst指数均大于水平序列的Hurst指数,说明竖向变形更易于趋于稳定;同时,各等时段的拟合度均趋于1,说明拟合效果较好,采用等时段分析得到Hurst参数的可信度也较高。

表5 等时段稳定性分析
对比上述分时段的分析结果,得出沉陷变形的稳定性具有时间演化特征,在不同阶段的稳定性有所差异,但总体表现为随时间的持续稳定性不断增加,验证了R/S分析对沉陷变形稳定性随时间变化分析的有效性。
2.3 变形预测分析
为对比分析各优化阶段的优化效果,先以L45监测点竖向变形为例,详述各优化阶段的预测效果,再利用水平变形预测来验证预测模型的有效性;同时,在预测过程中,以后4个周期样本为验证样本,并在以100 d等距增加外推预测3个周期,以判断地表沉陷的发展趋势。
首先,以预测结果的相对误差均值和训练时间为预测效果评价指标,得出3种激励函数的预测效果如表6。由表6可知,3种激励函数的预测效果存在明显差异,说明通过试错法确定最优激励函数的方法是可行的;对比三者的预测效果,得出Sigmiod型激励函数具有最小的平均相对误差和训练时间,预测效果相对最优,其次是Hardlim型和Sine型。因此,本研究确定激励函数类型为Sigmiod型。

表6 不同激励函数预测效果对比
其次,对10~16个隐层节点数的预测效果进行试算分析,结果如表7所示。由表7可知,不同隐层节点数的预测效果也存在明显差异,其中,隐层节点数为15时,平均相对误差仅为2.68%,训练时间为28.63 ms,预测效果相对最优,其余隐层节点数的预测效果相对略差,进而确定ELM模型的隐层节点数为15。

表7 不同隐层节点数的预测效果对比
最后,再利用粒子群算法优化ELM模型的连接权值和阈值,且为验证其优化效果,将其与前述隐层节点数优化结果进行对比分析,结果如表8所示。由表8可知,在相应验证节点处,通过粒子群算法的参数优化,预测结果的相对误差均不同程度地减小,进而说明其能有效提高预测精度;同时,其预测结果的最大相对误差仅为2.29%,平均相对误差为2.14%,预测精度较高,进而验证了本研究优化ELM模型在地表沉陷预测中的适用性;另外,通过外推预测可知,后续3个外推预测值均呈增加趋势,但增加频率相对较小,趋于向稳定方向发展。

表8 沉陷区竖向沉降预测结果
为验证该预测模型的有效性,再对L45监测点的水平位移进行预测研究,结果如表9所示。由表9可知,沉陷区水平位移预测结果的最大相对误差为2.49%,平均相对误差为2.17%,与竖向沉降预测结果相当,进一步验证了该预测模型的有效性;同时,外推预测结果显示,沉陷区的水平位移也会进一步增加,但增加速率较小,说明其水平位移也趋于向稳定方向发展。
根据前述分析,得出三河尖煤矿采煤沉陷区现阶段稳定性较好,后期沉降变形也趋于稳定,适宜采取后续土地复垦措施。

表9 沉陷区水平位移预测结果
3 土地复垦措施
为便于后续开展土地复垦工作,重点结合规范及工程实际,开展三河尖煤矿采煤沉陷区的土地复垦措施研究。
3.1 工程技术措施
3.1.1 表土剥离及堆放 剥离表层土壤以备复垦工程利用是土地复垦的常用方法。该方法可增强三河尖煤矿采煤沉陷区的土体利用率,减少复垦成本,且应妥善保管剥离土体,防止土质恶化,尽可能保持土体的原有土壤结构,以利于种植植物。
3.1.2 土地平整工程 由于地表沉陷具有不均匀性,如L45监测点的竖向沉降与水平位移存在差异,常使被损坏土地的表层起伏不平,难以进行有效的土地利用。因此,可以对沉陷区地表起伏不平的地区采取平整措施,确保土地坡度和平整度满足复垦标准。
3.1.3 土地翻耕 受多种因素的影响,地表土体常有土壤压实的现象,降低了雨水的渗透能力,为恢复该类土地的使用功能,可对其进行清理、翻松等,以疏松土壤,增强其渗透能力,并恢复其土壤结构。为达到此目标,可采取一定政策鼓励三河尖煤矿采煤沉陷区老百姓积极开展农业生产。
3.1.4 表土回覆 土地平整后要进行表层覆土,覆土来源主要有2个:一是原有土地表层剥离的土壤;二是建设主体工程剥离的表层土壤。项目区剥离的表土可以满足土地复垦的需求,覆土厚度根据复垦后土地利用方向的具体情况确定。
3.1.5 防护工程设计 当外排土场堆较高时,应按照“先拦后弃”的原则,预先设置挡土墙,且为保护排土场边坡冲刷,需增设截排水沟。
3.2 生物和化学措施
3.2.1 生物措施 生物措施是通过改善土壤环境,以恢复土壤肥力及生物活性的措施,如施加无机化肥措施等。该措施可有效增强复垦区的生物多样性,对区内的生态恢复和建设具有重要作用。
3.2.2 土壤改良 当复垦区土地肥力低下时,应采取消除危害物质,并围绕水、肥、气、热四大肥力要素进行土壤改良,且改良措施主要在管护期或耕种期进行,复垦期主要对土壤肥力特别低下的采取施肥措施。
3.3 监测措施
为保证环保设施的落实及正常运行,并验证环境影响的实际情况和环境保护措施的效果,需对复垦效果进行监测。复垦工作实施期间,至少每10 d对复垦实施措施监测1次,每季度对复垦实施情况和效果监测1次,依据复垦节点工期定期进行监测;管护期每年的监测频次控制在2次左右。
3.4 管护措施
土地复垦后期养护是生态复垦成败的关键,主要包括浇水、施肥、培土补植等,应根据土地复垦区的实际情况确定管护时间,且管护时间不宜少于3年,可根据后期实际情况进行调整。
4 结论
1)通过R/S分析在沉陷变形稳定性判断中的应用,得出该方法能有效评价沉陷区的沉陷稳定性,且能有效分析沉陷稳定性随时间的演化规律,可为土地复垦提供参考依据。
2)沉陷区土地复垦是一个系统工作,且势在必行,因此应结合矿区的复垦条件,合理规范复垦措施,提高土地利用率,在有效利用矿产资源的同时,也应保证生态环境的稳定。
3)通过变形预测研究,得出本研究的预测模型的预测精度较高,适宜于沉陷区变形预测,且预测结果得出沉陷区变形趋于向稳定方向发展。
4)土地复垦前的沉陷稳定性评价及变形预测研究具有重要的作用,可为后期开展土地复垦研究奠定理论基础,值得进一步深入研究。

