品读教材，把握教学

刘姗姗

摘要：角的初步认识的教学，基于学生对常见的平面图形已有了直观的认识。于学生而言，“角”比长方形、正方形、三角形等平面图形更为抽象。教材上对于“角”没有具体明确的定义，学生知道这样的图形是“角”即可。基于这种教学要求，学生在“什么样的图形是角？”这一问题的理解上，多数存在着一些认知误解。但是，随着笔者研究教材，发现教材中对于“角”的认识有着巧妙的安排，教师可以根据教材的安排，帮助学生去认识角，理解角。

关键词：小学数学;教材研读;课堂教学

教学角的初步认识之前，苏教版教材已经安排了常见的平面几何图形的教学。在教学角的初步认识时，除了需要考虑从实际物体中抽象出角之外，也要适当考虑学生在平面几何图形方面已有的知识经验[1]。学生已经初步认识长方形、正方形、三角形等常见的平面几何图形，知道这些图形都有角，说明学生对角的认识已经有了一个模糊的轮廓。笔者经思考后决定，在认识角之前，先帮助学生把“角”的轮廓变得清晰一些，明确角是平面图形的一部分，角与平面图形是部分与整体的关系。于是，在课堂教学的导入环节，笔者进行了如下设计：

教师出示四根小棒摆在黑板上。

师：这有四根小棒，你能用四根小棒，摆一个我们学过的图形吗？

師：这是什么图形？

生：正方形。

师：去掉一根小棒。可以怎么摆？

师：这是什么图形？

生：三角形。

师：再去掉一根小棒。这是什么图形呢？

生：三角形的一个角。

师：这种新的平面图形是角。三角形中有角，还有哪些图形有角？

生：正方形、长方形、梯形……

师：角是图形的一部分。

从学生已知的平面几何图形中抽象出角，学生对“角”会有一种“熟悉感”，对后面角的特征的教学，起到一定的促进作用。

一、教材呈现的“角的表象”

教材呈现手工课上的情境，学生可以从三角尺、纸工袋和钟面上找出角。三角尺上的角是一个锐角，纸工袋上的角是一个直角，钟面上的角是一个钝角，这三种角帮助学生丰富角的表象。这三个物体中，钟面上形成的角其实是一个“活动角”，这也是角由静到动的一个演变。为了体现教材的这一用意，在展示钟面上的角时，笔者在钟面上“拨”出角，学生经历了角形成的过程，既可以吸引学生的注意力，也体会到角是可以变化的。

学生在“时分秒”的学习中，已经充分认识了钟面，为了体现钟面上时针和分针的走动引起角的变化，需要符合钟面上时针走的慢，分针走的快这一常识。基于此，笔者在“拨”角的过程中注意到一个问题，钟面上的时间是2时55分，“拨”角的时候，时针、分针由重合到分开，体现角形成的过程。如果从2时10分开始拨，分针要旋转大半圈，为了不让学生对角产生错误的认知，笔者把钟面上的时间调整为10时55分，在教学时，笔者把钟面上的时间由10时55分拨到11时15分，形成一个钝角。这样，既保留了角丰富的表象，又体现出角由静到动的一个变化。为后面教学角的大小做好了铺垫。

二、教材呈现的“角的特征”

角的特征是“角有一个顶点和两条直直的边”还是“角有一个顶点和两条边”？很多教师总结出角的特征是前者。我们回归教材，发现教材上茄子老师是这样总结的：“角有一个顶点和两条边。”基于此，笔者和其他教师进行了商讨，学生通过比较发现角的特征这一环节可以进行简化，学生发现角都有一个尖尖的地方（顶点）和两条线（边）即可。教师说明尖尖的地方是角的顶点，两条线是角的边，从而总结出角的特征。为了便于学生明确角的边是直直的，教师可以在角的特征之后提出“角的两条边是怎样的？”这一问题，帮助学生正确清晰地认识角。

师：这些角有什么共同特征？

生：他们都是尖尖的。

师：尖尖的地方在哪里？谁来指一指。

生：都有线。

师：每个角都有几条线？

生：每个角都有2条线。

师：这个尖尖的点是角的顶点。这两条线是角的边。

师：角有几个顶点和几条边？

生：角有一个顶点和两条边。

师：角的两条边是怎样的？

生：角的两条边是直直的。

……

角的标记是容易被教师忽略的一个知识点。教师向学生讲解角的特征之后，一般会说：“我们通常用一个弧线表示这是一个角。”教师轻飘飘一句带过，大部分学生并不知道为什么要用弧线来表示角，学生就会对角有一个错误的认知：“一个顶点和两条边是角。”但是角指的是两条边叉开的区域。如何让学生意识到角指的是两条边叉开的区域呢？笔者在帮助学生指角时，就渗透了这一问题。

师：生活中处处有角，比如我们平时常用的工具：三角尺、数学书、钟表。今天老师把它们请到了教室里。你能找打他们身上的角吗？

师：谁来指一指三角尺上的角。（学生在上面点了一下）他在三角尺上点了一下，我把他指的角画在黑板上。这是角吗？角应该怎样指呢？如果指这个角，从这个点出发，这样指，再从这个点出发，这样指，这是一个角。你学会了吗？你来指一指。你学的真快。大家拿出1号三角尺找到这个角，指一指。

笔者在向学生讲解“这是一个角”时，会在角的两条边之间用手指比划一个弧度，学生根据这个动作就会体会到角指的是两条边之间的区域。接下来由学生自己指角。

三、教材中“角的大小”的呈现

教材安排学生自己做出一个活动角，通过变化活动角，体会角是有大小的。学生每人有一份配套的组合活动角，方便学生制作。笔者发现想想做做第5题，安排学生进行折纸，学生会折出大小不同的角。受这一启发，学生发现角有大小这一环节，笔者设计了三种做角的方式，分别是：用大小相同的圆片彩纸折角、用小棒做角以及画角，学生选自己喜欢的方式做角。

在交流学生做的角时，我采用以下方式：先选一位同学画的角进行全班交流，学生说一说这位同学画的角好不好，好在哪？再选两位同学折的角，让学生对比这两个角有什么不同的地方？为了减少变量，笔者为学生提供的彩纸是大小相同的圆片，学生发现用圆片折出的角大小不同，引发学生对角的大小的认知需求。最后选一个学生做的较大的活动角，教师拿出两根比较长的小棒问：“老师也来做一个活动角，我做的活动角肯定比你们大！同意吗？”引起学生的思考。

师：大家创造出了各种各样美丽的角。（教师展现三种角，大的折角，小的折角，大的活动角）

师：这两个是折出的角，老师把两个角标出来。他们除了颜色不同，还有哪里不同？（大小不同）

师：通过比较，我们知道角是有大小的。

师：这是用小棒做成活动角，老师这里有更长的小棒。教师拿出来。我做出来的角肯定比你们的大！（教师做一个比较小的角）停顿两秒，你同意吗？

情况1：同意 老师做一个比较小的角。

师：为什么你刚刚同意呢？（觉得边比较长，就大）

情况2：不同意

学生上来摆一摆，让刚刚同意的学生来说说为什么同意。（觉得边比较长，就大）

师：角的边长，角一定大？（不是）角的边短，角一定小？（不是）

总结：角的大小和变得长短无关。

师：你能吗？

学生上来拉开

师：他是怎么做到让绿色的角变得比蓝色的角大？

生：拉開角的边。

师：准确地说，把角的两条边叉开。我们发现角的两条边叉开的越大，角越大。

师：你能让你的活动角比绿色的角小吗？你是怎么做的。

生：角的两条边叉开的越小，角就越小

师：角的大小和什么有关。

生：角的大小和边叉开的大小有关。

明确：角的大小与边的长短无关。和叉开的大小有关。

通过解读教材，可以把角的大小问题平稳合理的进行过度，而不是突兀的去研究角的大小问题。

四、教材“巩固练习”的安排

教材上的想想做做一共安排了5题，其中第5题笔者稍微改变之后，做了角的大小的引入。剩下4题分别是：辨角、数角、角有大小以及角的大小是可以借助工具比较的。由于角比较抽象，笔者在认识角的第一课时为了帮助学生理解“什么是角？”对教材的例题做了如下教学。

想想做做第1题，可以帮助学生辨角，重点让学生说一说为什么这个图形不是角？最后总结为什么剩下的图形是角？

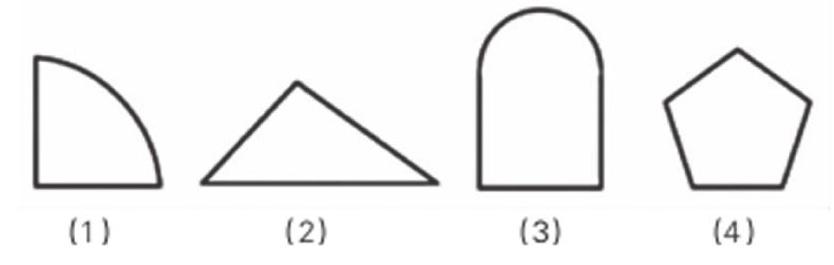
想想做做第2题，学生独立数出图形中角的个数，图（2）、图（4）学生比较顺利地找到了角，然而图（1）、图（3），有个别学生认为没有角。

师：为什么？

生：因为角的两条边都是直直的，而它们的边到了上面就弯了，所以没有角。

这时其他学生也开始迟疑，也觉得图（1）、图（3）没有角。

这部分学生只能判断出规则图形中的角，却判断不出有曲线图形中的角[2]，说明他们没有处理好角与图形是部分与整体的关系。教师要进行适当的引导。

想想做做第3题，学生能比较出三个角的大小关系，并说明原因即可。

想想做做第4题，学生通过动手，了解到三角尺上的角可以作为比较角的工具。

角的初步认识的教学，是虚实结合的[3]。在图形概念的生成过程中，教师既要重视“实”这一方面，让学生通过对实物的观察角、摸角、制作角、对比角来感受角的基本特征，同时又要重视“虚”这一方面，要指导学生在充分观察的基础上去想象、抽象出角，生成角的概念，理解角的性质。

参考文献：

[1]沈江.基于认知心理 体验知识内涵[J].小学数学教育，2018（5）.

[2]朱莹.儿童视角的图形教学[J].小学数学教育，2016（11）.

[3]于芳.图形教学的有效性思考[J].小学数学教师，2014（5）.