核电厂安全壳地震概率风险评估
王晓磊,吕大刚,阎卫东
(1.沈阳建筑大学 土木工程学院,辽宁 沈阳 110168; 2.哈尔滨工业大学 土木工程学院,黑龙江 哈尔滨 150090)
核电厂通常面临内部事件和外部事件双重威胁,2011年日本福岛核事故后,核电厂抵御地震等外部事件的能力受到广泛关注。核电厂抗震安全评估通常采用两种方法:抗震裕量评估(SMA)[1]和地震概率风险评估(SPRA)[2]。SPRA是从全概率角度的核电厂抗震裕量评估方法,可全面考虑抗震安全评估中包含的多种不确定性。
SPRA可分别基于地震风险解析函数和风险卷积函数实现。地震风险解析函数由于具有能够直接给出地震风险解析解的优点,在国外核工程领域得到广泛应用。美国ASCE43-05规范[3]基于地震风险解析函数,给出了一致风险设计方法,研究表明:基于地震风险解析函数设计的核电厂结构地震风险与精确的卷积函数计算结果较为接近。Kennedy[4]采用ASCE 43-05方法将基于地震风险解析函数与卷积函数计算结果进行比较,发现对于多个厂址,基于地震风险解析的结果与精确的卷积积分结果均较为接近。安全壳是核电厂最后一道安全屏障,其在地震作用下的完整性对核电厂安全至关重要。地震风险解析函数在我国核电厂安全壳结构地震风险评估中的适用性研究,对我国核电厂安全壳SPRA具有重要借鉴意义。
本文推导地震风险解析函数,分析地震风险解析函数蕴含的两个假设和两个近似,基于地震风险解析函数和风险卷积函数分别计算我国核电厂安全壳地震概率风险,分析地震风险解析函数蕴含的两个近似在我国核电厂安全壳结构地震风险评估中的适用性。
1 地震风险解析函数
1.1 地震风险解析函数推导
地震风险可由地震易损性函数和地震危险性函数卷积计算[5]得到:
(1)
(2)
式中:PF为地震风险;a为地震动强度参数变量;H(a)为危险性函数;FC(a)为易损性函数。
有学者研究发现地震动强度服从极值Ⅱ型分布,那么危险性函数可进一步表示为:
(3)
危险性函数通常超越概率较小,可简化为幂指数函数形式:
(4)
式中:KH为形状参数;kⅠ为位置参数;u为尺度参数。
地震易损性函数通常假设为对数正态分布形式。如果对数正态分布函数中不确定性标准差以本质不确定性的对数标准差和知识不确定性的对数标准差平方和开平方的形式表示,那么该函数被称为均值易损性函数[6],可进一步表示为:
(5)
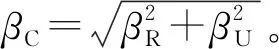
对地震易损性函数求导,可表示为:
(6)
将式(4)和式(6)代入式(1),可得:
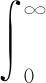
(7)
取x=lna,M=lnaC,式(7)可进一步表示为:
(8)
取x=y-M,则式(8)可转换为:
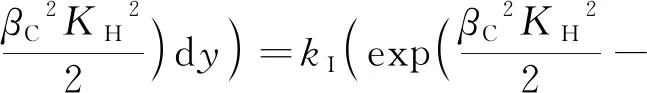
(9)

由对数正态分布性质可得:
(10)
式(9)可简化为:
(11)
式(11)可转化为地震风险解析函数为:
(12)
(13)
1.2 地震风险解析函数蕴含的假设和近似
由上述地震风险解析函数的推导过程可发现:地震风险解析函数蕴含两个假设和两个近似。两个假设分别为:地震动强度函数服从极值Ⅱ型分布,地震易损性函数服从对数正态分布;两个近似分别为:将幂指数函数近似为极值Ⅱ型分布函数,地震危险性幂指数函数中两个参数kⅠ和KH不随地震动强度参数变化,即将地震危险性函数中的局部性参数近似为整体性参数。
2 我国某核电厂安全壳结构地震概率风险评估
2.1 某核电厂厂址的地震危险性分析与一致危险谱生成
我国核电厂厂址地震危险性曲线通常基于中国概率地震危险性分析(c-PSHA)[7]方法得到,c-PSHA方法的计算公式为:
P(Y≥y) = 1-
(14)
式中:P(Y≥y)为地震动强度参数大小为y的超越概率;P(Y≥y|mj,(x,y)ki,θ)为指定震级mj、位置(x,y)ki和方向角θ的地震发生条件下,地震动强度参数大小为y的超越概率;f(θ)为方向角概率密度函数;fki,mj为空间分布函数;νk为地震年平均发生率;Aki为潜在震源区的面积;βk=bln 10,b为古登堡-里克特公式;m0为起算震级;muzk为最大震级;Δm为最小震级区间。
基于c-PSHA方法,我国某核电厂厂址地震安评报告给出了我国华南地区某核电厂厂址的概率地震危险性数据,基于评估报告中的地震危险性数据,绘出厂址一些有代表性的地震危险性曲线,如图1所示。图1中:PGA为峰值地震动加速度;Sa为谱加速度;IM为地震动强度参数。
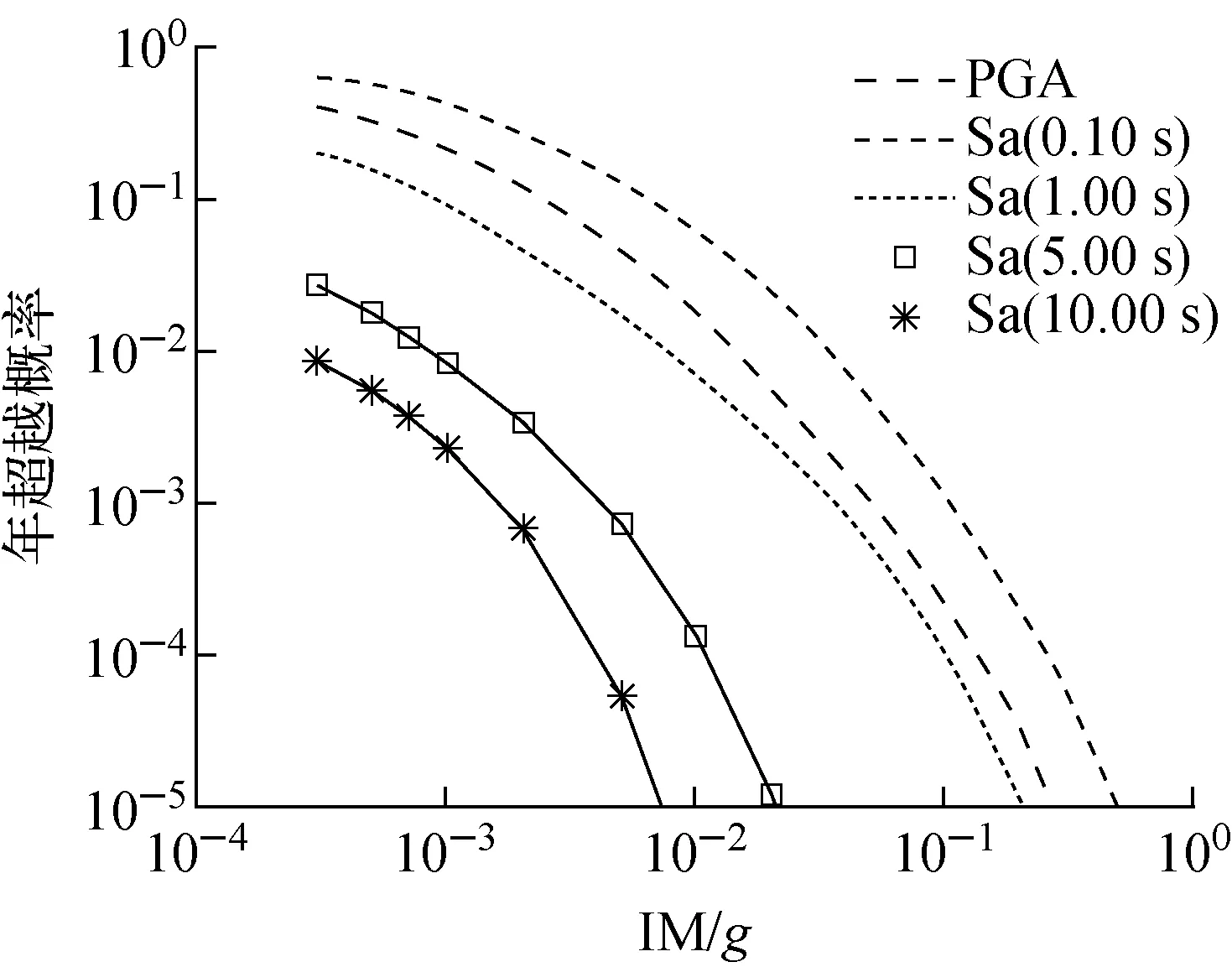
图1 地震危险性曲线Fig.1 Seismic hazard curve
基于所有强度参数的概率地震危险性数据,取指定超越概率可得到一致危险谱。一致危险谱在所有周期强度参数具有指定的超越概率,概率信息比较明确,在核电厂设计和评估中得到广泛运用。我国华南地区某核电厂厂址安全报告给出了超越概率0.000 1(万年一遇)和0.000 01(十万年一遇)的一致危险谱数据,如图2所示。图2中,T为周期。
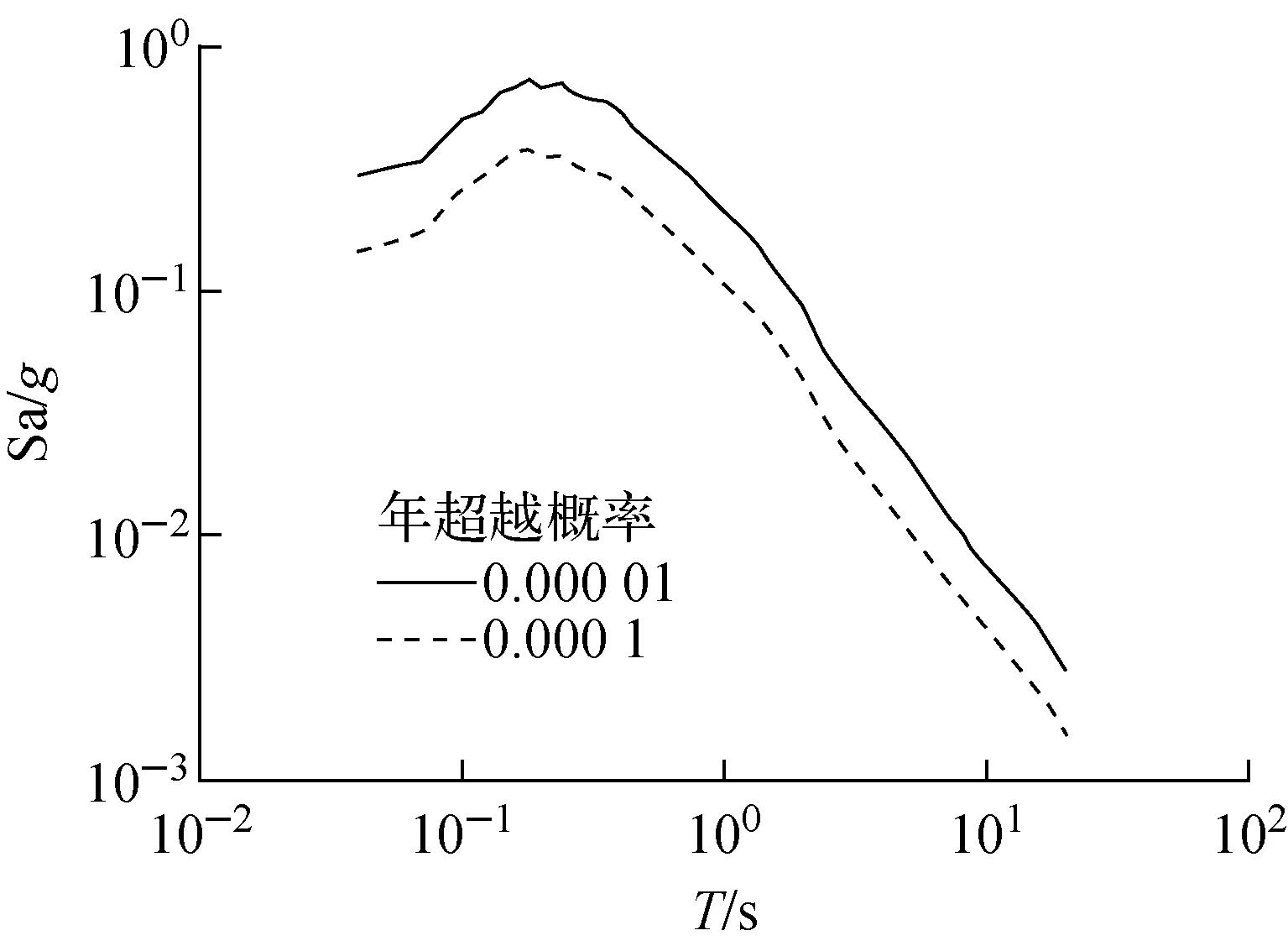
图2 一致危险谱Fig.2 Uniform hazard spectrum
2.2 安全壳结构地震易损性分析
1) 地震易损性安全系数法
安全系数法[8]是目前核电厂结构地震易损性分析常用的分析方法。核电厂结构抗震能力[9]可表示为:
A=AmeReU
(15)
式中:A为核电厂抗震能力;Am为核电厂抗震能力中位值;eR和eU分别为本质不确定性和知识不确定性的随机变量,假设服从对数正态分布。
安全系数法将抗震能力表示为设防地震能力与安全系数F乘积的形式:
A=FASSE
(16)
式中,ASSE为安全停堆级抗震能力。
安全系数F进一步可表示为:
F=FS·Fμ·FRS
(17)
式中:FS为强度系数;Fμ为塑性能吸收系数;FRS为结构响应系数。
强度系数FS可表示为:
(18)
式中:S为某种失效状态下单元的抗震能力;RN为非地震荷载下的单元响应;RT为所有荷载作用下(包括地震荷载)的单元响应。
塑性能吸收系数Fμ可表示为:
Fμ=(ρμ-q)r
(19)
式中:ρ=q+1;q=3.00δ-0.30,δ为临界阻尼;r=0.48δ-0.08;μ为系统延性。
结构响应系数FRS可表示为:
FRS=FSA·FSD·FM·FMC·Fδ·FEC·FSSI
(20)
式中:FSA为谱型和地震动系数;FSD为随着深度地震动输入折减系数;FM为建模系数;FMC为模态组合系数;Fδ为阻尼系数;FEC为地震分量的组合系数;FSSI为土-结相互作用系数。
(21)
(22)
(23)
βFRS=
(24)
2) 某核电厂安全壳地震易损性分析
假设安全壳在地震中处于塑性状态时结构失效。安全壳结构应力应变关系可表示为三线性骨架曲线模型[10],如图3所示,取第1个拐点为安全壳极限状态,此剪应力极限值τ1[10]为:
(25)
式中:FC为混凝土抗压强度;σV为竖向压应力。

图3 三线性骨架曲线Fig.3 Trilinear skeleton curve
本文分析对象是我国华南地区某核电厂反应堆厂房,其三维剖面图[11]如图4a所示,将核反应堆三维厂房等效为集中质量梁单元模型[11],如图4b所示。安全壳和筏板基础集中质量梁单元模型节点和单元信息以及材料参数参见文献[11],基于OpenSees开源有限元程序进行建模。
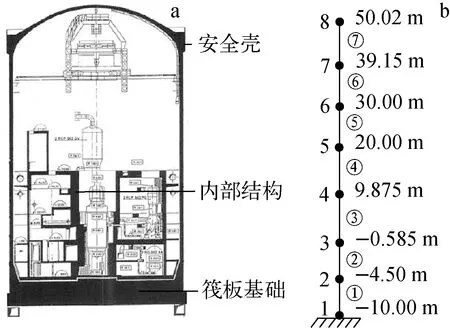
图4 某反应堆厂房剖面图(a)和安全壳 与筏板基础集中质量梁单元模型(b)Fig.4 Schematic view of reactor building (a) and lumped mass and beam model of containment and raft foundation (b)
运用安全系数法,选用超越概率为0.000 1的一致危险谱为厂址谱,基于振型分解反应谱法,计算系数FS,其他参数采用文献[12-13]中的经验数据,取经验数据范围的中位值,最终计算得到易损性曲线,如图5所示。
2.3 基于地震风险解析函数的安全壳地震风险
地震风险解析函数中的地震危险性函数需简化为幂指数函数形式:
H(a)≈kIa-KH
(26)
美国ASCE43-05规范给出了KH的确定方法:
(27)
(28)
式中:HD为设防地震水准,ASCE 43-05规范取为0.000 1(万年一遇);Sa0.1HD为0.000 01超越概率(十万年一遇)的Sa;SaHD为0.000 1超越概率(万年一遇)的Sa。
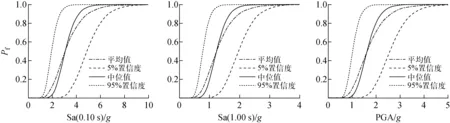
图5 基于一致危险谱的安全壳地震易损性曲线Fig.5 Seismic fragility curve of containment based on uniform hazard spectrum
基于式(26)~(28)计算了我国某核电厂厂址地震危险性近似拟合函数参数,结果列于表1,地震危险性曲线与近似函数的比较如图6所示。由图6可见:近似函数在HD和0.1HD超越概率范围内具有较好的拟合效果,但是在大于HD和小于0.1HD范围,拟合函数会高估地震危险性水平,即由ASCE 43-05确定的常数KH和kⅠ只是地震危险性数据的局部近似。

表1 地震危险性近似拟合函数参数Table 1 Parameter of seismic hazard approximation fitting function
基于上述确定的KH和kⅠ数据,利用地震风险解析函数(式(12))可计算核电厂安全壳地震风险水平,计算结果列于表2。基于风险解析函数的计算结果表明安全壳结构地震风险较低。
2.4 基于卷积的安全壳地震风险
地震风险可由地震易损性函数和地震危险性函数卷积计算得到,卷积函数见式(2)。本文利用精确的数值卷积方法,分别采用两种形式计算上述华南地区某核电厂安全壳结构地震风险:1) 采用实际地震危险性数据;2) 采用地震危险性极值Ⅱ型分布函数,分布函数的参数由ASCE 43-05方法确定,且KH和kⅠ不随地震动强度参数变化。两种形式最终计算结果列于表3。
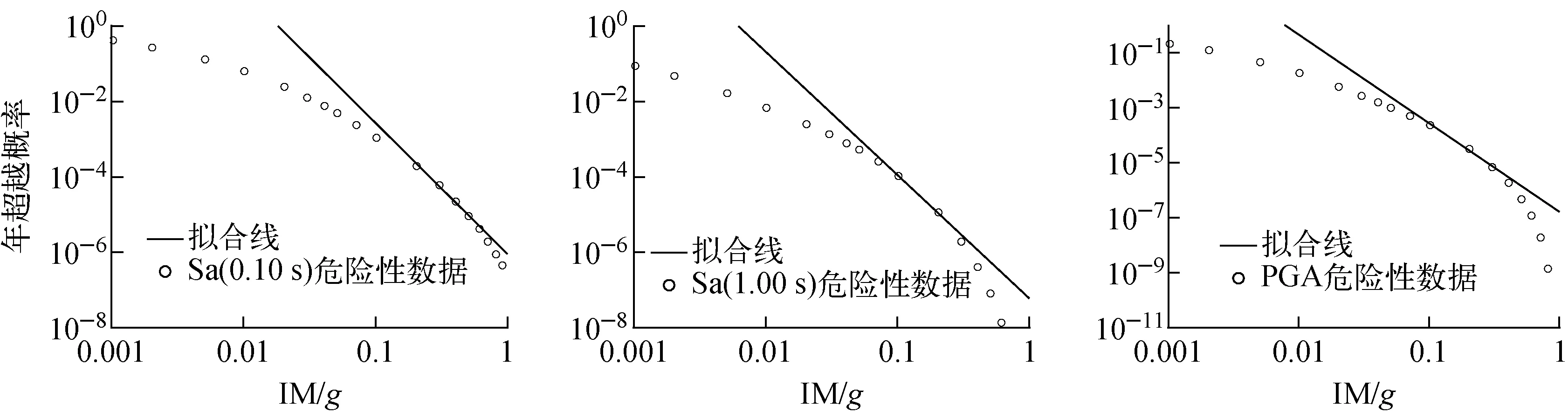
图6 地震危险性曲线与近似函数的比较Fig.6 Comparison of seismic hazard curve and approximation fitting function

表2 基于地震风险解析函数的安全壳地震风险Table 2 Seismic risk of containment based on analytical function of seismic risk

表3 基于卷积的安全壳地震风险Table 3 Seismic risk of containment based on numerical convolution
本文将第1种卷积风险计算结果与基于地震风险解析函数计算结果进行比较,分析地震危险性幂指数函数中两个参数kI和KH不随地震动强度参数变化对地震风险的影响;将第2种卷积风险计算结果与基于地震风险解析函数进行比较,分析幂指数函数近似极值Ⅱ型分布函数对地震风险结果的影响。将表2、3中的计算结果进行比较可发现:地震危险性幂指数函数近似极值Ⅱ型分布对地震风险计算结果没有影响,对于本文我国某算例厂址,采用ASCE 43-05方法确定的地震风险解析函数会高估安全壳地震风险。基于风险卷积的计算结果表明安全壳结构地震风险较低。
2.5 地震风险解析函数适用性分析
Kennedy[4]发现基于地震风险解析函数分析的核电厂结构地震风险结果与精确的卷积结果近似相等,但本文研究发现地震风险解析函数计算结果明显大于精确卷积公式计算结果,即高估了地震风险。分析原因如下:ASCE43-05的目标是设计出具有一致目标风险的结构、系统和部件,目标风险定为10-5,而我国某核电厂安全壳结构的安全裕量储备较大,面临的实际地震风险较小,在10-8~10-10量级左右,明显小于ASCE 43-5的目标风险10-5,所以对于抗震裕量较大的结构,基于地震风险解析函数分析的地震风险通常会较为保守。地震风险简化公式能直接给出地震风险解析函数,计算比较直接且方便,但在某些情况下,计算结果会高估结构的地震风险,建议将地震风险解析函数运用在我国核电厂安全壳等结构的初步地震风险评估中。
3 结论
本文推导了地震风险解析函数模型,分析了地震风险解析函数蕴含的两个基本假设和两个近似,基于地震风险解析函数和风险卷积函数,评估了我国某核电厂安全壳结构地震风险,分析了地震风险解析函数在我国核电厂安全壳地震风险评估中的适用性,并给出了应用建议,得出以下结论。
1) 地震风险解析函数包含两个基本假设:地震动强度函数服从极值Ⅱ型分布,地震易损性函数服从对数正态分布。
2) 地震风险解析函数包括两个近似:地震危险性解析函数由幂指数函数局部近似,kⅠ和KH不随地震动强度大小发生变化的局部近似。
3) 地震危险性函数由幂指数形式近似极值Ⅱ型分布对风险计算结果没有影响。
4) 针对本文算例厂址,地震风险解析函数中KH和kⅠ为常数的局部近似会高估安全壳面临的地震风险,未来我国核电厂运用该模型进行风险分析时,要适当考虑该规律影响。
5) 我国核电厂安全壳结构地震风险水平较低,具有较高的抗震裕量。
6) 建议将地震风险解析函数运用在我国核电厂安全壳等结构的初步地震风险评估中。

