基于ANSYS Workbench对单螺旋榨油机榨膛温度分布情况的研究

李芃荃，谭雪松，张黎骅，李 举

(四川农业大学 机电学院，四川 雅安625000)

螺旋榨油机被广泛运用于植物油料中的油脂提取，通过对榨油机某些关键技术的研究，能够保障榨油质量的同时增加油脂产量，可节约时间和人力成本[1]。目前世界范围对螺旋榨油机的研究较少，理论经验不足，缺乏有效的试验验证。影响榨油机性能的因素有很多，其中温度是对榨油机出油率及出油质量影响最大的因素之一[2]。榨油机工作时, 主要通过榨膛内部油料粒子之间、油料与螺杆及油料与榨膛之间的摩擦生热来维持所需的温度，但这种平衡模式是比较难保持的[3-5]。国内生产螺旋榨油机的核心部分是榨膛[6]，而加热装置大多放置在榨膛上，通过导热的方式为榨料提供压榨时的温度条件，因此对榨油机榨膛温度的研究很有必要。

温度属于热力学范畴，对于热力学来说，包括稳态热力学分析(系统的净热流率为零)和瞬态热力学分析(系统加热或冷却的过程)，榨油机工作时，对于榨油机榨膛自身结构来说，属于稳态热传导问题[7]。有限元方法常用来解决稳态热传导问题,常用的有限元软件有ANSYS Workbench、SDRC/I-DEAS等[8]。其中ANSYS Workbench仿真平台能对复杂机械系统的结构静力学、结构动力学、刚体动力学、流体动力学、结构热、电磁场以及耦合场等进行分析模拟，其强大的功能以及简便的操作已成为国际最流行的有限元分析软件之一[9]。到目前为止，国内还未有用ANSYS Workbench来研究榨油机榨油时适宜温度范围的先例。本文旨在运用ANSYS Workbench对单螺旋榨油机榨膛温度分布进行研究，并提出此方法可用于预测榨膛内外壁温度分布。

1 材料与方法

1.1 试验材料

本试验使用CH 1500T 家用单螺旋榨油机(功率1 500 W，榨螺转数30～50 r/min，处理量1.5 kg/h)，对新疆薄皮核桃仁进行压榨试验。密封袋、HT-866红外测温仪、电子称、卷尺、秒表等。

1.2 试验方法

为方便测量榨膛外壁温度，用卷尺测量榨膛全长190 mm,从左到右每5 mm选取一个点，选点时错开榨膛出油孔，均匀选取36个点，由于红外测温仪光斑大小为2～3 mm，故测点坐标误差以毫米为单位。测点位置如图1所示。

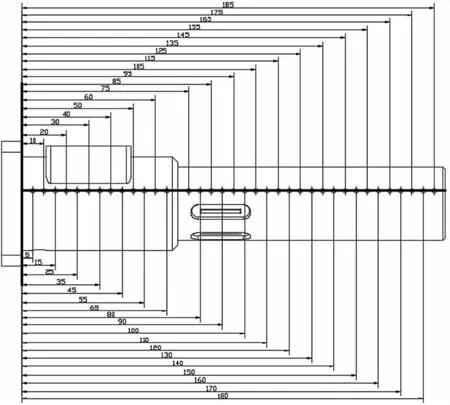
图1 榨膛外表测温点示意图

试验步骤：①将剥好的核桃仁掰成小块，平均分为6组，每组80 g。②检查榨油机，接通电源，空转调试，确保榨油机能够正常工作。③记录试验时间、试验地点、环境温度以及榨膛各测点的初始温度，待榨油机工作前榨膛外壁各测点的平均温度与室内环境温度基本一致时开始试验。④完成试验1(无预热)，记录试验压榨时间为4 min以及试验后榨膛外壁指定各点对应的温度数据。⑤完成试验2～6(预热5 min)，记录试验压榨时间皆为4 min(确保压榨时间一致)，记录试验结束后各测点的温度。⑥计算并记录试验2～6结束后各测点温度的有效平均值，统计各对应点的平均温度，以此作为试验榨膛外壁各对应点温度。

2 结果与分析

2.1 试验温度测试结果(见表1、表2)

经检查调试以后，该榨油机可以正常工作。由试验1可知，若不预热不易出油，并且各个测点所对应的温度(见表1)变化不大，不宜用来作为分析温度变化的数据(试验室温为25℃，试验前测得所有测点的平均温度为24.3℃，误差在可忽略不计的范围以内)。

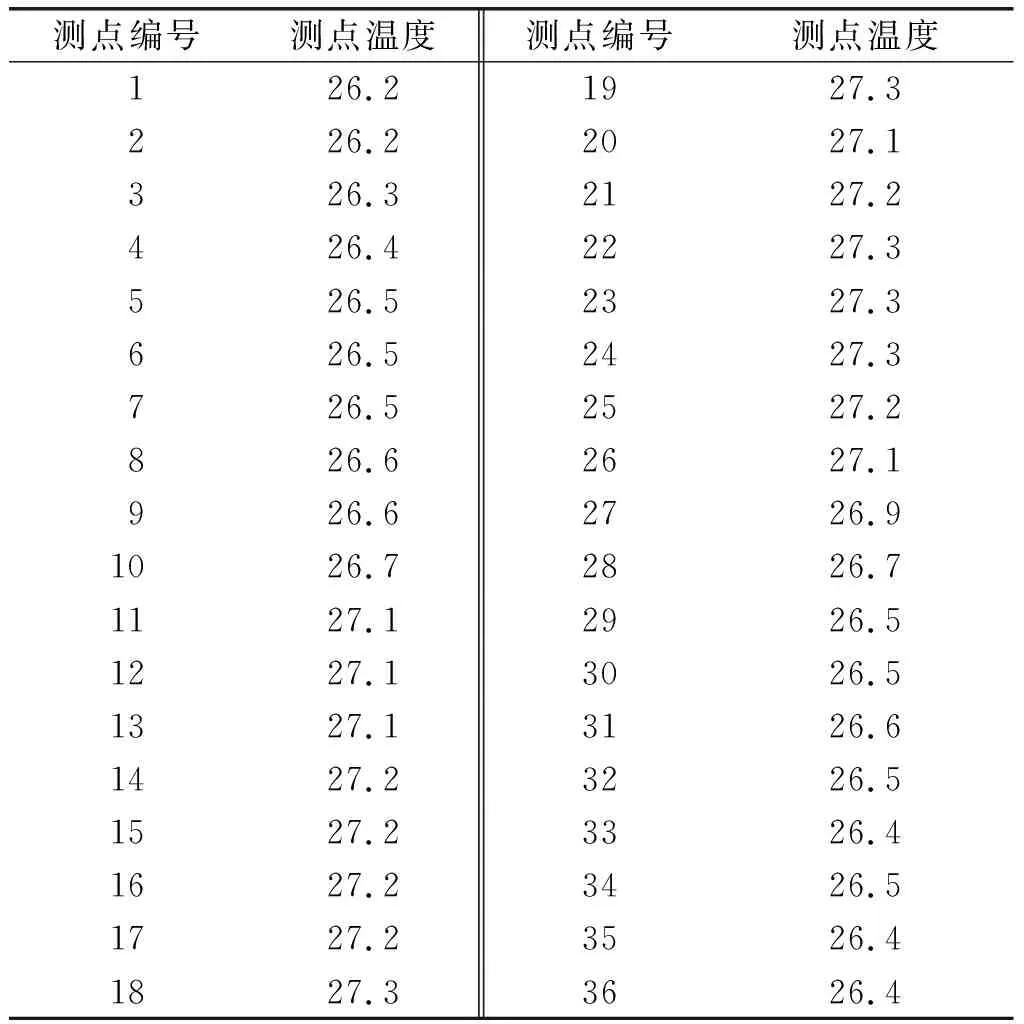
表1 试验1榨膛外壁温度 ℃

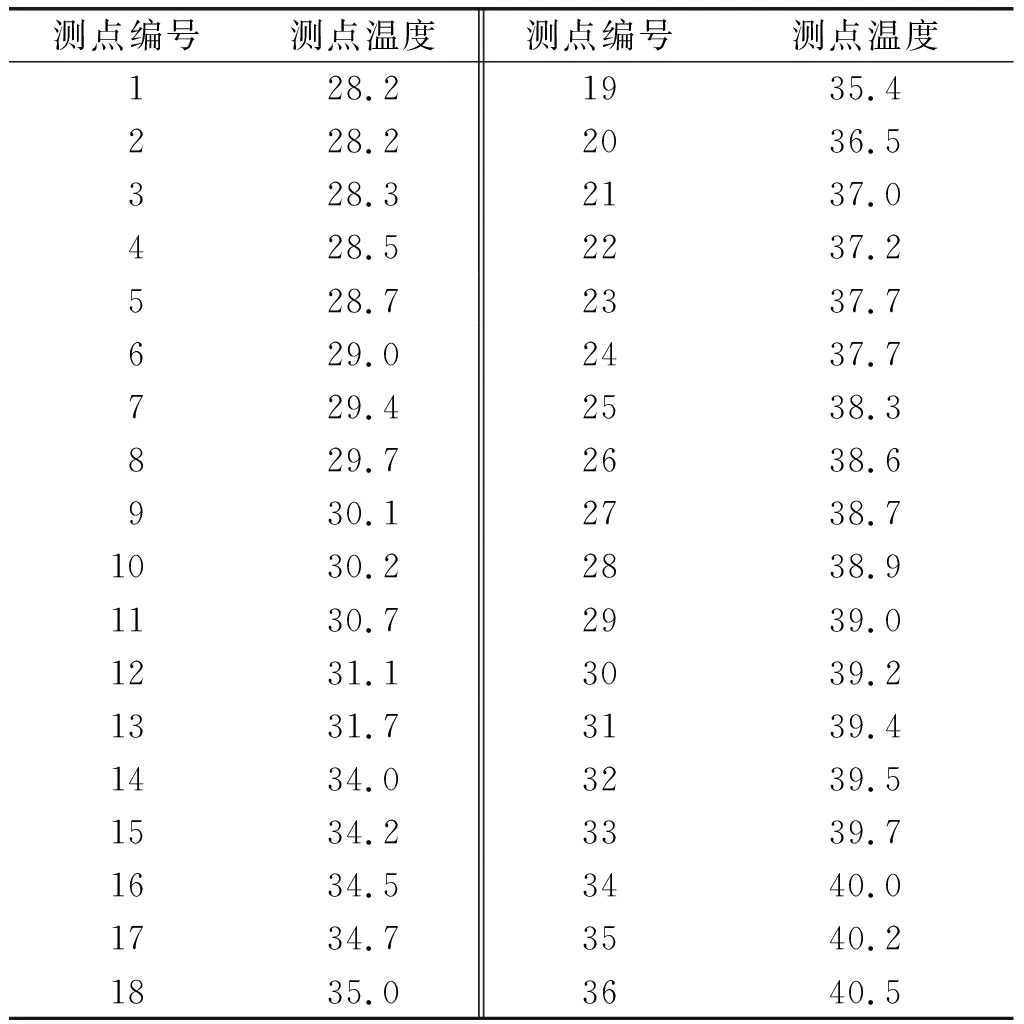
表2 试验2～6榨膛外壁平均温度 ℃

记录预热时间为5 min的5组试验的榨膛外壁测点温度，并求得榨膛外壁平均温度如表2所示(试验室温为25℃，5组试验前所有测点的平均温度分别为24.6、24.4、24.7、24.5、24.2℃，误差在可忽略不计的范围以内)。

2.2 单螺旋榨油机榨膛稳态热仿真

基本传热方式有热传导、热对流及热辐射3种。

在稳态热分析中任意一节点的温度不随时间变化，稳态热分析的能量平衡方程为：[K]{I}={Q}。式中：[K]是传导矩阵，包括热系数、对流系数及辐射系数和形状系数；{I}是节点温度向量；{Q}是节点热流向量，包含热生成。在ANSYS Workbench中利用模型几何参数、材料热性能参数以及所施加的边界条件，自动生成[K]、{I}、{Q}。

2.2.1 建立有限元模型设置材料特性

在Solidworks中把模型另存为(.igs/stp)格式，打开ANSYS Workbench，将其导入Steady-State Thermal图形窗口中，经过Solid Model Facets等操作将模型实体化, 如图2所示。并添加材料属性，本文中榨膛的材料为304不锈钢。

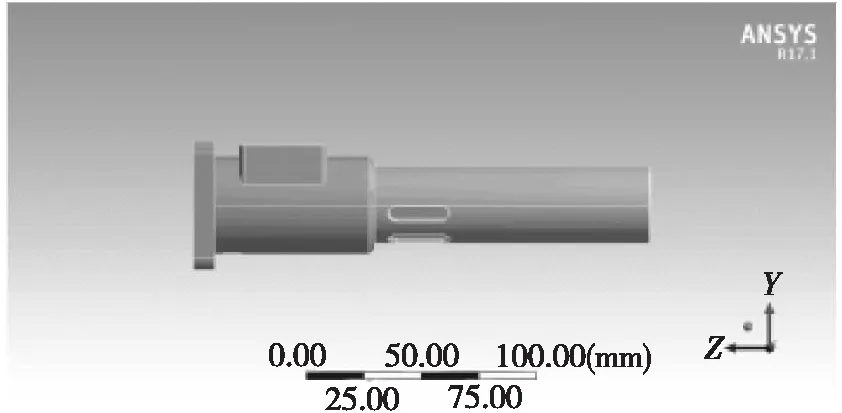
图2 榨膛简易模型导入示意图

2.2.2 定义接触区域并网格划分

以5 mm为单位间隔，从榨膛左侧到榨膛右侧依次选取36个测量点。本文采用Solid87(六节点四面体单元)划分方式进行划分，因为Solid87在热仿真中对于不太规整的结构比较适合，并且精度较高，对结果的准确性提供了保障依据，将Mesh中的Patch Conforming Method设置为Tetrahedrons，并把Details of Mesh中的Relevance调制成100。最终如图3所示将榨膛划分成117 704个单元72 502个节点。

图3 榨膛简易模型划分单元格示意图

2.2.3 施加载荷和边界条件进行求解

假设环境温度恒定，在Steady- State Thermal的Initial Temperature中设置初始环境温度为25℃，在Convection的Film Coefficient中选中Import Temperature Dependent后选择Stagnant Air—Simplified Case。然后将榨膛外壁从右到左指定36个点的温度导入ANSYS Workbench中，并进行求解得到榨膛温度分布云图，如图4所示。

图4 榨膛简易模型导入温度示意图

因为此时无法再在榨膛内壁标定点，所以用等比例的方式在榨膛内部从右往左选取第1、2、3、5、7、9、10、11、13、15、17、19、20、21、23、25、27、29、30、31、33、35、36测点的对应温度，共23个，如图5所示。

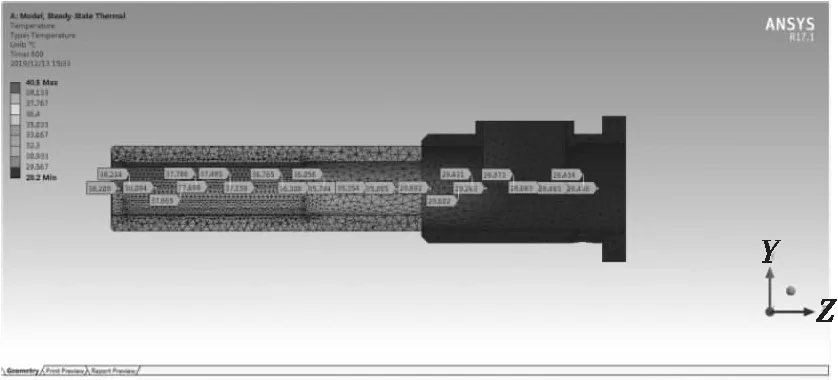
图5 榨膛简易模型内壁温度示意图

2.2.4 反解榨膛外壁仿真温度

将榨膛当成一个整体，在内壁添加同样的边界条件、网格划分方式，选取测点1对应的榨膛内壁仿真温度加载在榨膛内表面(选中Steady-State Thermal的Temperature，将Magnitude设置为28.436℃)，通过ANSYS Workbench热仿真得到榨膛外壁仿真温度，重复22次以上步骤得到榨膛内、外壁23个仿真温度，如表3所示。

2.3 单螺旋榨油机榨膛内外壁热仿真温度误差

通过试验和仿真得到榨膛外壁23个对应点的温度，如表4所示。由表4可知，在测点36(185 mm，40.5℃)取得最大误差为6.274%，平均误差为2.44%，由于最大误差和平均误差都小于10%，所以对于该农业机械来说误差是在可接受范围以内的，因此可以用仿真温度替代实际测量的温度用于后面的温度曲线拟合。

通过Matlab可以将23个榨膛外壁仿真温度拟合成如图6的函数，其函数表达式为f(x)=0.065 859x+27.463，且取得的最大误差为6.191 3%，对于农业机械来说，误差低于10%，同样满足拟合精度。

榨膛内壁仿真温度拟合函数如图7所示，其函数表达式为f(x)= 0.067 098x+27.514 1，且取得的最大误差为6.279 2%。

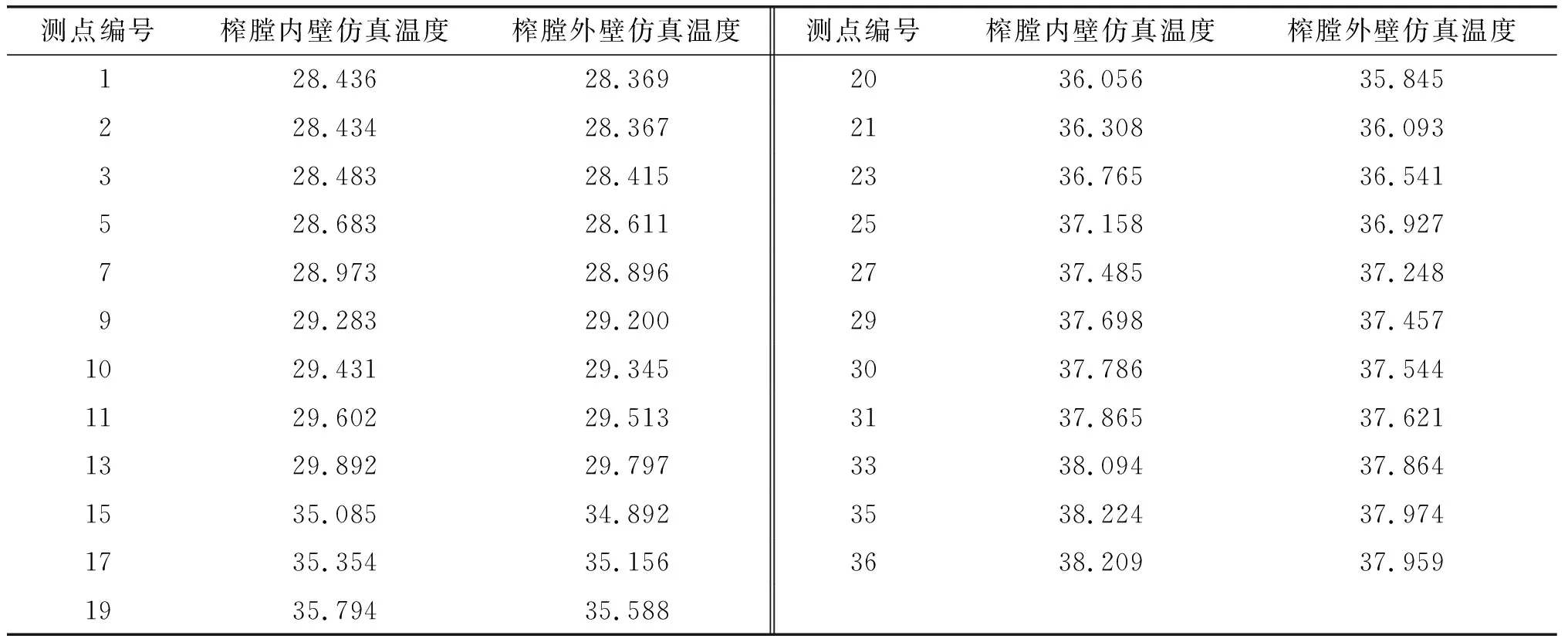
表3 榨膛内、外壁仿真温度 ℃

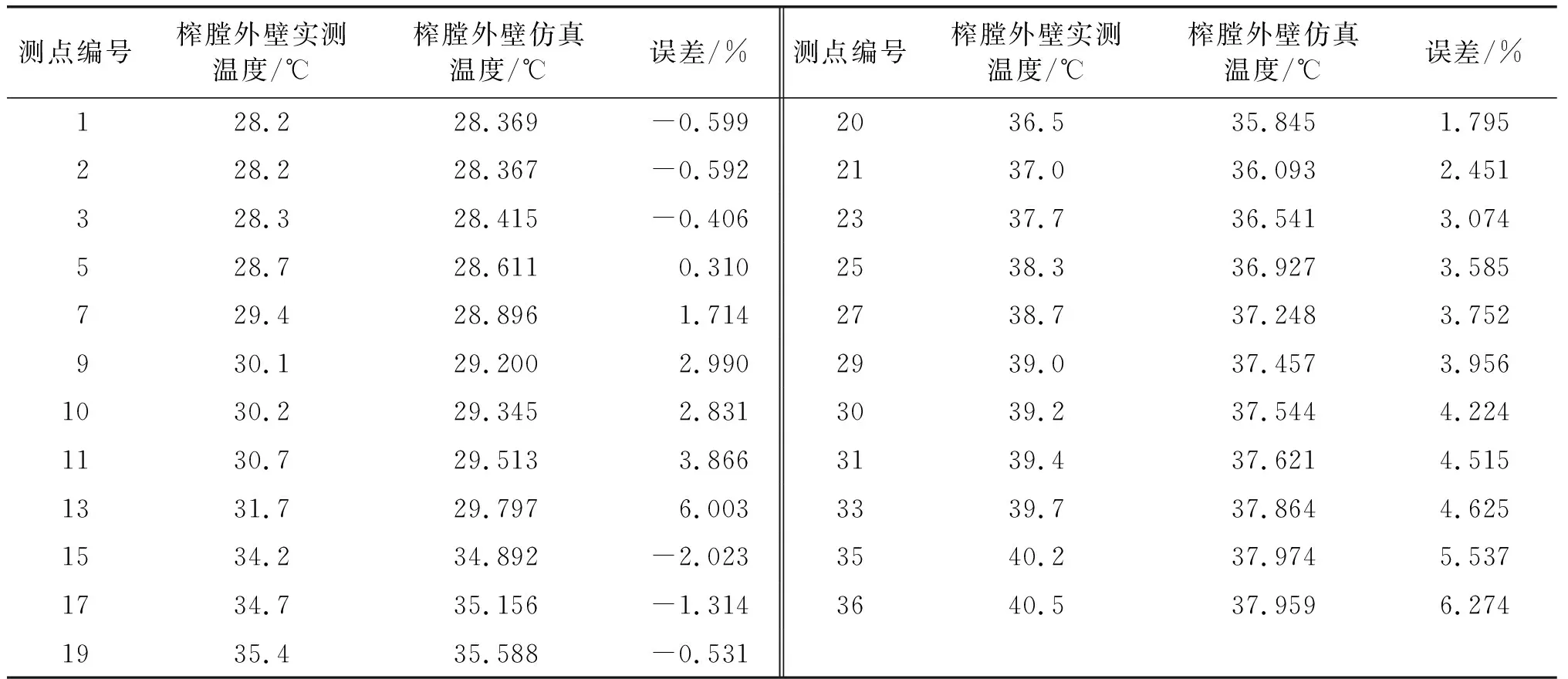
表4 榨膛外壁实测温度与仿真温度

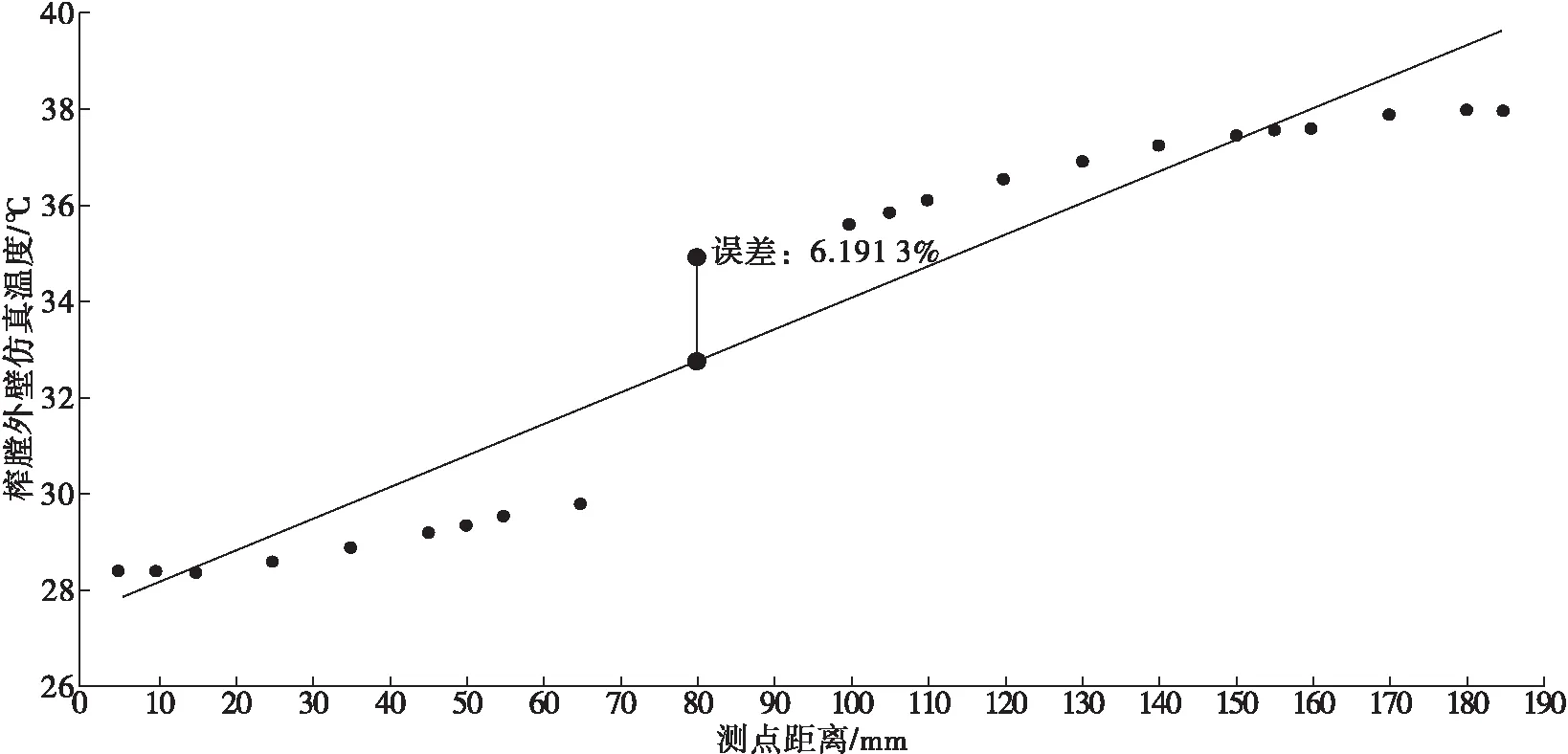
图6 榨膛外壁仿真温度拟合函数示意图

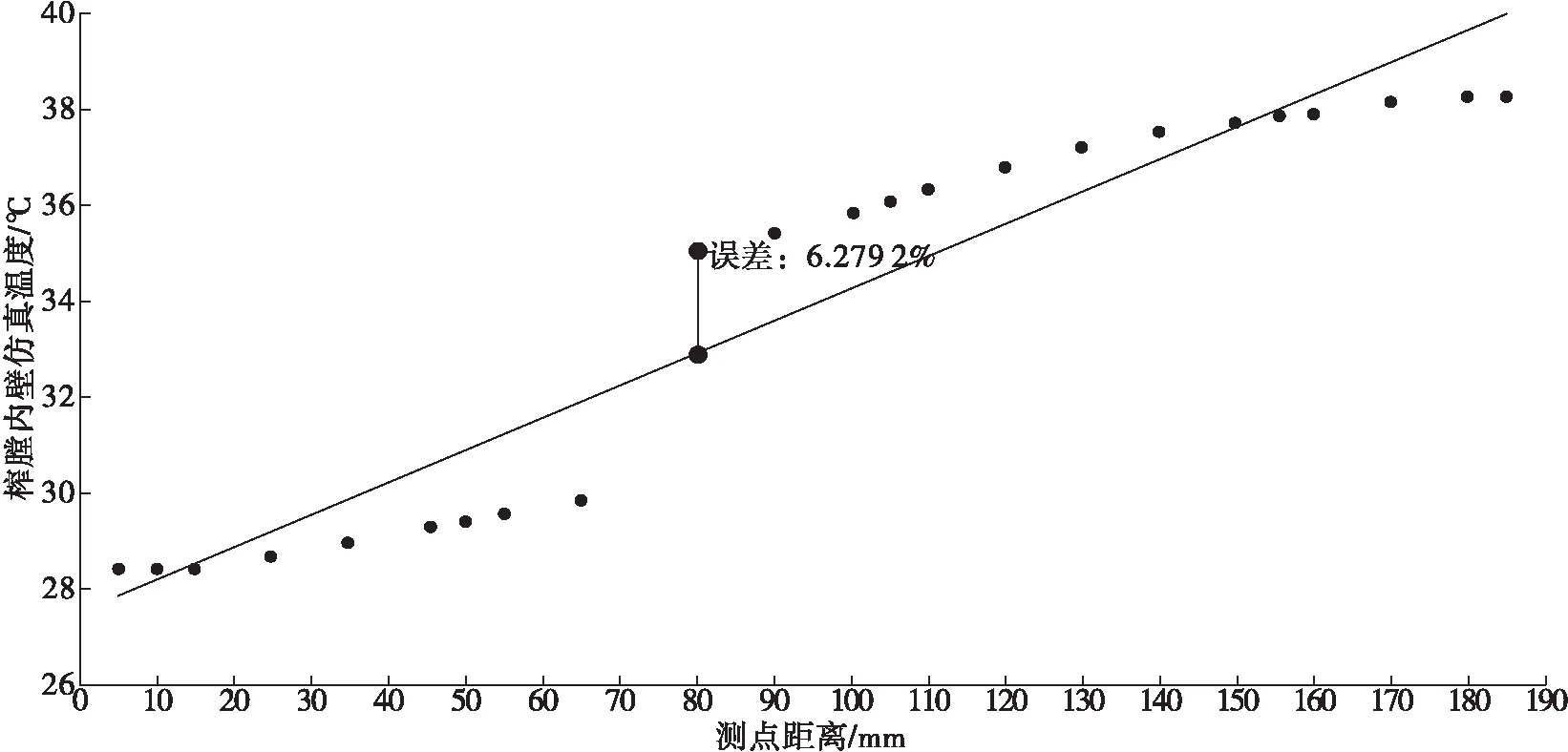
图7 榨膛内壁仿真温度拟合函数示意图

2.4 单螺旋榨油机榨膛外壁仿真结果验证

为了验证本文热传导仿真结果的准确性，在榨膛外壁选取36个测点剩下的13个测点，在拟合通过仿真得到的榨膛外壁温度的曲线上求得对应的13个测点的温度，并与实际测得的温度进行比较，如表5所示。

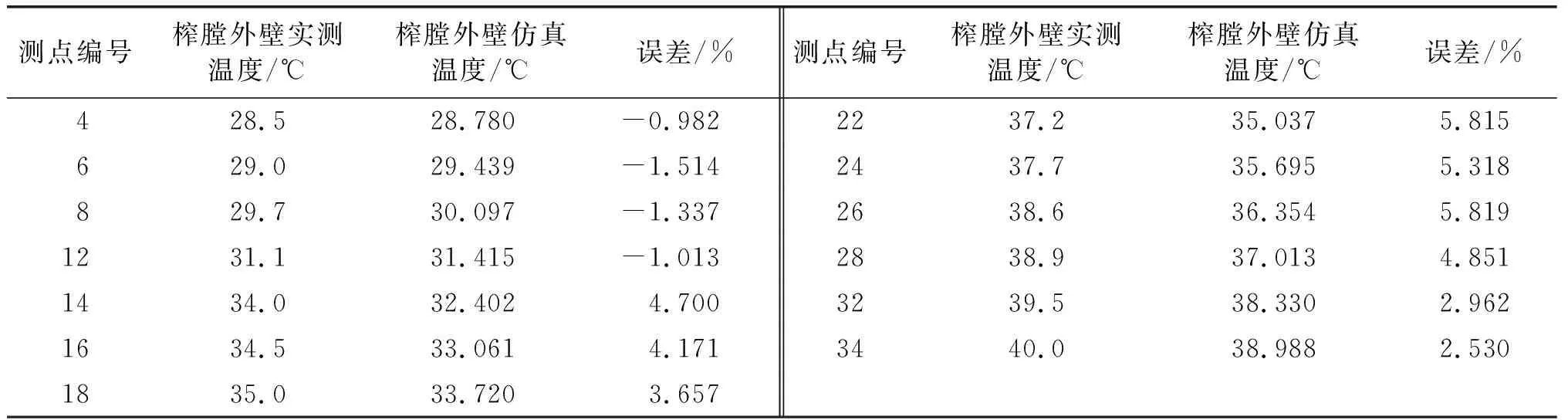
表5 榨膛外壁实测温度与仿真温度

由表5可知，剩下13个测点的榨膛外壁实测温度与仿真温度的最大误差为5.819%。因此，这种热传导反解问题的方式是可以用来预估榨膛压榨时内外壁温度分布以及压榨温度范围的。

3 结 论

利用ANSYS Workbench软件对CH 1500T单螺旋榨油机的榨膛进行网格划分以及稳态传热仿真，得到榨膛内外壁相应测点的温度。对比榨膛外壁实测温度与仿真温度，误差范围在-2.023%～6.274%之间,对于农业机械来说此误差范围在可接受范围内(低于10%)，从而验证了可以运用ANSYS Workbench来预测榨膛内外壁温度分布。