复杂地形对风关海洋环境噪声特性影响

衣雪娟，林建恒，江鹏飞，孙军平，单元春,2

(1. 中国科学院声学研究所北海研究站，山东 青岛 266114；2. 中国科学院大学，北京 100049)

海洋环境噪声是海洋中的固有声场，其研究始于二战期间，利用环境噪声实测数据总结出的Knudsen谱[1]和Wenz曲线[2]现在仍然是水声工程中经常使用的背景场参考曲线。随着水声学的发展以及声呐技术对背景场需求的日益增加，人们在持续开展海洋环境噪声实验研究[3-8]的基础上，着手海洋环境噪声的理论建模以及利用环境噪声数据反演海面、海底参数等技术[9-11]进行研究。按照适用于海洋环境来分，目前海洋环境噪声模型主要分为2类：1)适于分层介质海洋环境的二维噪声模型[12-14]，将海水介质沿深度分若干层，水平方向视为均匀，仅考虑海洋信道多种环境因素作用下不同分层相关参数的变化：如声速分布、海面和海底的反射以及介质的吸收等；2)考虑环境参数随水平距离或方位变化情况的三维海洋环境噪声模型[15-18]。实际海底地形往往非常复杂，包括浅海大陆架、向深海延伸的大陆坡，以及海山、海沟、岛礁等，这些地形的起伏对海洋波导中的声传播具有重要影响[19]。海洋环境噪声理论建模是基于所关注海域的环境噪声源模型和声传播模型，因此实际环境中模型的仿真需要深入了解海山、岛礁等复杂海底地形对海洋环境噪声的影响，关注复杂海底地形引起的海洋环境噪声建模的难度和仿真分析计算量的增加。

本文依据现有的海洋地形数据库，针对真实的复杂海底地形—海山/岛礁海域，采用射线三维声传播的N×2D和3D算法，建立了适于复杂地形海域的风关海洋环境噪声理论模型，研究复杂地形海域的海洋环境噪声特性。为了突出海底地形对风关海洋环境噪声特性的影响，假设风关噪声源随机均匀分布且声速剖面不随距离和方位变化。

1 复杂地形海域风关海洋环境噪声模型

由于射线法对高频声传播计算具有独特优势，计算简洁，适于求解深、浅海，特别是深海与距离有关环境的声场，结果直观、物理意义清晰明确，因此模型选取了射线三维声传播模型。利用射线声传播模型的N×2D和3D算法：采用柱坐标系，假设垂直接收阵位于z轴，将三维海洋环境按水平方位角划为N个扇区(见图1)，计算每个位于方位扇区中心角度上声源至接收点的声场，叠加后获得接收点的总声场。N×2D和3D算法的区别在于后者考虑了方位分区之间的声耦合(即2个相邻垂直扇区之间能量交换)，因此3D算法精度高，适于计算涉及地形剧烈起伏或海洋水团变化等引起的声线水平折射问题，但3D算法的计算时间明显高于N×2D。若认为海洋环境在水平方位变化不太剧烈，声传播在水平方位上的耦合甚小于深度方向耦合，则采用N×2D算法更便捷、经济。

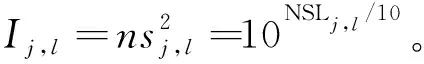
(1)

式中ψj和ψl是0～2π均匀分布的随机数，代表距离和方位2个方向的随机相位信息。

图1 水平方位分区示意Fig.1 Schematic diagram of sectors division by azimuth

噪声场空间分布特征通常用两点声场复共轭积的系综平均表示，称为噪声互谱密度，它代表了噪声场的空间特性，定义为：

C(z1,z2)=〈Φ(z1)Φ*(z2)〉

(2)

式中：*表示复共轭；〈〉号表示系综平均。将式(2)展开，本文考虑水平均匀分布的噪声源(l=m和j=n部分)互不相关，即假设不同网格单元(l≠m和j≠n)的噪声是不相干的，则噪声互谱密度可近似为：

(3)

接收点z1的声压值可通过射线传播程序计算获得：

(4)

式中：φ为相位；ξ为声线索引，表示掠射角为αr的不同声线；A为声压振幅。

令z1=z2，对方程(3)两边取对数获得接收深度z1处的环境噪声强度级：

SL(z1)=10lg〈|Φ(z1)|2〉

(5)

考虑接收阵含有Np个垂直阵元，各阵元的声场可用列向量的形式表示：

Φ=col[Φ(zn)]，n=1,2,…,Np，

(6)

式中：col[ ]表示列矢量，Φ(zn)为每个接收阵元的复声压。入射平面波阵响应向量可表示为：

q(α,β)=col[qn(α,β)]

(7)

式中：qn(α,β)=exp(-ikxn)；k为平面波矢量；c0是接收阵位置的声速；β和α分别为方位角和俯仰角。

噪声场垂直指向性用矩阵向量来表示：

|q*(α,β)·Φ|2=qH(ΦΦH)q

(8)

噪声场垂直指向性的均值为：

〈|q*(α,β)·Φ|2〉=qHCnoiseq

(9)

式中Cnoise=〈ΦΦH〉为平均的噪声互谱密度矩阵。

2 复杂地形海域风关海洋环境噪声仿真

本文选取近海山/岛礁海域，对复杂地形海域风关海洋环境噪声进行数值仿真，主要对接收点全方位接收的海洋环境噪声级随深度的变化、全方位海洋环境噪声垂直指向性等特性进行讨论。在仿真海洋环境噪声之前，首先分析几种海底地形方位的传播损失。

2.1 仿真计算海域环境

依据海底地形数据，选取某海山/岛礁海域用于数值仿真计算海洋环境噪声特性，其海底地形见图2，垂直接收阵所在位置用★表示，该处海深为1 368 m；考虑50 km范围(在图中使用圆形标注)内的海面噪声源进行模型仿真计算，接收点正北方向的方位角为0°，按1°的步长将360°方位角沿顺时针方向划分为不同的扇区；计算频率为1 kHz，声速剖面采用深海声道形式(见图3)，在本文计算范围所对应的海区，声速剖面基本呈现负梯度形式。

图2 海底地形、接收位置和计算范围Fig.2 Seabed topography, receiver location and calculation range

图3 声速剖面Fig.3 Sound profile

2.2 不同方位的声传播损失

各水平方位分区的海底地形不同，海底引起的反射也不同，导致各方位的声传播损失不同，因而在相同噪声源情形下，地形不同的方位区，对接收点海洋环境噪声的贡献不同。本文首先计算3种显著不同海底地形所在水平方位的声传播损失。

图4是不同方位区间的海底地形变化图，方位范围分别为144°～160°、200°～220°、300°～320°，对应方位区间内最高海山的高度分别约为1 300、600和150 m。

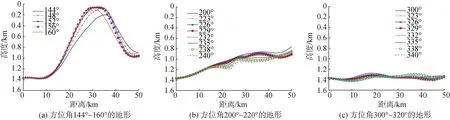
图4 不同方位角区间的海底地形Fig.4 Seabed topography for different azimuth sectors

图5分别是N×2D算法计算的不同方位角区域内声源深度为200、800 m时，3条不同掠射角度的声线轨迹。图中的黑粗实线是海底深度线，实线、虚线、点划线分别代表掠射角0°、10°、20°的声线轨迹。由于计算海深范围内声速基本呈负梯度分布，声线均会与海底接触。在海底是海山的情况下，声线与海山斜坡每接触一次，其掠射角就会发生改变，改变量与斜坡的坡度成正比。在3种海底地形中，图5(a)、(b)的海山高、坡度大，声线掠射角改变最大，声线轨迹变化也最大，同时相对于图5(a)中深度200 m、图5(b)中深度800 m的0°掠射角声线能够越过海山顶部继续向前传播，表明负梯度声速剖面和高海山情况下，更远距离的海面噪声能够以0°掠射角声线到达大深度的接收点；图5(c)、(d)中的海山坡度相对较缓，声线掠射角改变量相对较少，其轨迹变化没有图5(a)、(b)中的剧烈，因此在深度200 m的接收点，更多的海面噪声能够以上述3种掠射角声线的形式到达，而在800 m深度，海面噪声只有掠射角20°的声线能够到达，表明在负梯度声速剖面和小坡度海山情况下，200 m深接收点的海面噪声能量要高于深度800 m的接收点；图5(e)、(f)的海底相对平坦，声线轨迹只发生微小的改变，同样在负梯度声速剖面情况下，200 m深接收点的海面噪声能量略高于深度800 m的接收点。上述声传播损失计算结果表明用N×2D算法在负梯度声速剖面条件下，对于坡度大的海底山，远处海面噪声源更容易到达深度深的接收点；而对于坡度小的海山和近似平坦海底，远处海面噪声源则更易到达接收深度浅的位置。

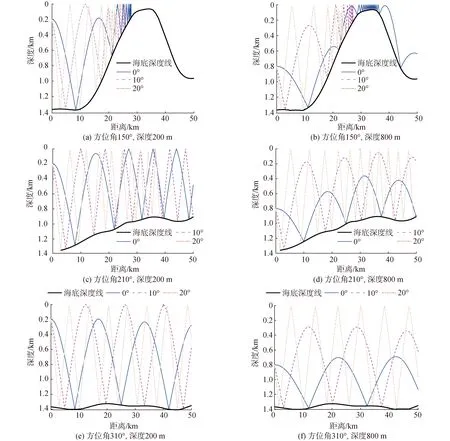
图5 不同方位区域和深度的3条声线轨迹Fig.5 Ray trajectories for different azimuths and depths

对于存在海山/岛礁海底地形的海域，位于不同位置的接收点，受到海底山/岛礁声反射的作用不同，导致不同位置的接收点环境噪声特性明显不同，下面针对图2所示复杂海底地形，对接收点距离海底山/岛礁较远和较近2种情形，仿真计算讨论风关海洋环境噪声级和垂直指向性。

2.3 接收点距离海山较远的仿真结果

取图2中的海底地形实际数据，接收点位于海山/岛礁群中间，距离海山较远，与其周边最近的海山/岛礁主峰的距离达20～40 km。图6给出接收点海洋环境噪声级均值(1 kHz)随接收深度变化的数值仿真结果。2种算法的接收点噪声级在近海面处均随深度小幅增加，此后降低，不同的是随着接收深度的进一步增加，N×2D的噪声级结果基本趋于稳定，而3D的结果则一直持续小幅度降低，600 m海深内3D计算值稍高于N×2D，600 m以下海深3D计算值稍低于N×2D，二者在相同深度的差值均在4 dB以内。

从海底地形图中可以观察到接收点的东北、东南方向均存在海底山，图7是N×2D和3D算法计算得到的各方位扇区(1°)内海洋环境噪声级随深度和方位角的变化情况，可以看出，二者的噪声级随方位变化均有起伏，N×2D的噪声级较大值位于海山高度较高的方位区域(如150°方位附近)，并且在此方位区内，噪声级较大的接收点位置较深；而海山较低的方位区域(如200°方位附近)，噪声级较大的接收点位置较浅。3D算法计算得到的水平方位分区噪声级，量级区间要大于N×2D，噪声级较大的接收点和深度，主要在海面以下几百米的深度范围内，且随水平方位角呈基本均匀分布(与N×2D结果明显不同)。从图7可以看出，3D的扇区噪声级随方位变化的趋势(即高、低噪声强度对应的方位区间)与N×2D基本相似，只是二者的量值不同。应该说明的是，本例接收点位于海底山/岛礁群围中，四周边海底山/岛礁的反射效应，致使该点处形成近海面数百米深度处噪声级较高，3D计算模型考虑了各扇区声场的耦合，即计及水平分区之间的能量交换，基本反映了上述各种声场效应作用的综合结果。

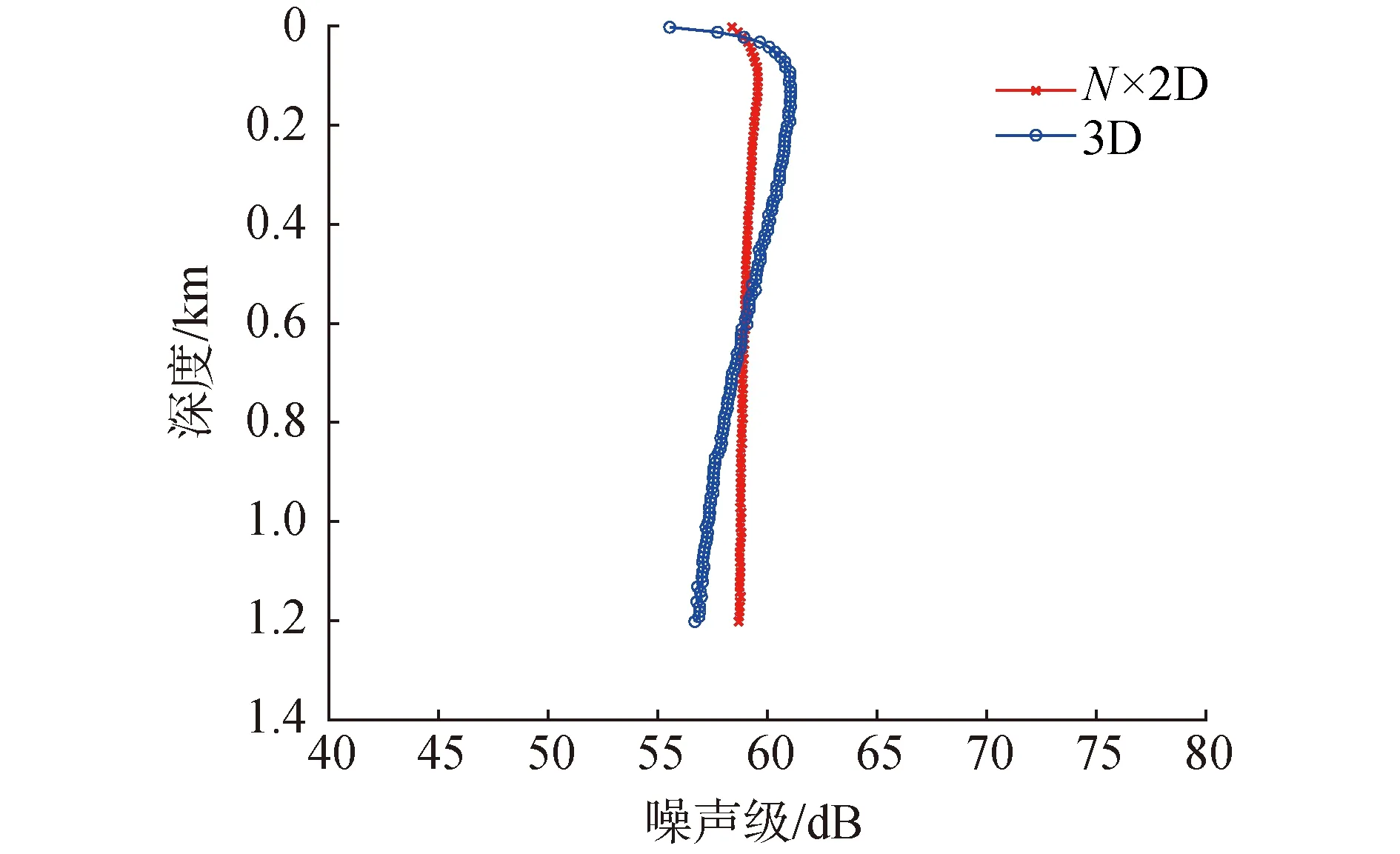
图6 风关噪声级随深度变化Fig.6 Wind-generated noise level vs depth

图7 风关噪声级随深度、方位角的变化Fig.7 Wind-generated noise level vs depth and azimuth

图8是N×2D和3D算法计算得到的各方位海洋环境噪声垂直指向性变化情况(1 kHz)，垂直阵元间隔0.7 m，首阵元深度100 m，末阵元深度121.7 m。从图中可以看出2种算法的指向性结果变化趋势基本相似：在海底较平坦的方位角区域(如310°附近)，噪声垂直指向性的结构较为稳定，存在常见的海洋环境噪声凹槽；而在存在海山的方位区，由于海山高度的不同，噪声垂直指向性形状的变化较大，环境噪声凹槽的深度得到不同程度的填补，其宽度也随之发生变化；但N×2D结果在各方位的最大值一般位于水平凹槽的左右两端或者俯仰角接近零度方向，3D结果在全方位都会存在靠近海面方向的较大值。

2.4 接收点距离海山较近的仿真结果

改变垂直接收阵的位置，如图9所示，使其与东面的岛礁群的距离更近(约数km)，该接收点海深约240 m，其东南方位计算范围内也存在海山，计算时采用的声速剖面仍如图3所示。图9画出了距接收点50 km范围(图中圆圈)内的海山/岛礁情况。

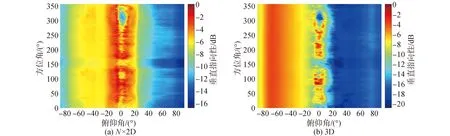
图8 风关噪声垂直指向性随方位角变化Fig.8 Vertical directionality of wind-generated noise vs azimuth

图9 海底地形、接收位置和计算范围Fig.9 Seabed topography, receiver location and calculation range

图10是上述接收点四周不同方位区间的海底地形变化图，其中图10(a)、(b)、(c)对应的方位区间分别为：44°～60°，62°～100°，250°～280°；10(a)、(b)方位内分布着不同高度的海山，10(c)方位内深度随接收距离增大而逐渐变深。

图11是用N×2D和3D算法计算该接收点位置的海洋环境噪声级(1 kHz)随深度变化，N×2D与3D算法的结果变化趋势相似，基本都是随深度缓慢增加，二者在同样深度的差值最大接近3 dB。

图12是N×2D和3D算法得到的各方位扇区风关噪声级随接收深度和方位角的变化，两者的仿真结果变化趋势较为相似，存在海山/岛礁方位区域内的噪声级均较高，并且在此类方位内，3D计算噪声级略高于N×2D结果。

图10 不同方位角区间的海底地形Fig.10 Seabed topography for different azimuth sectors

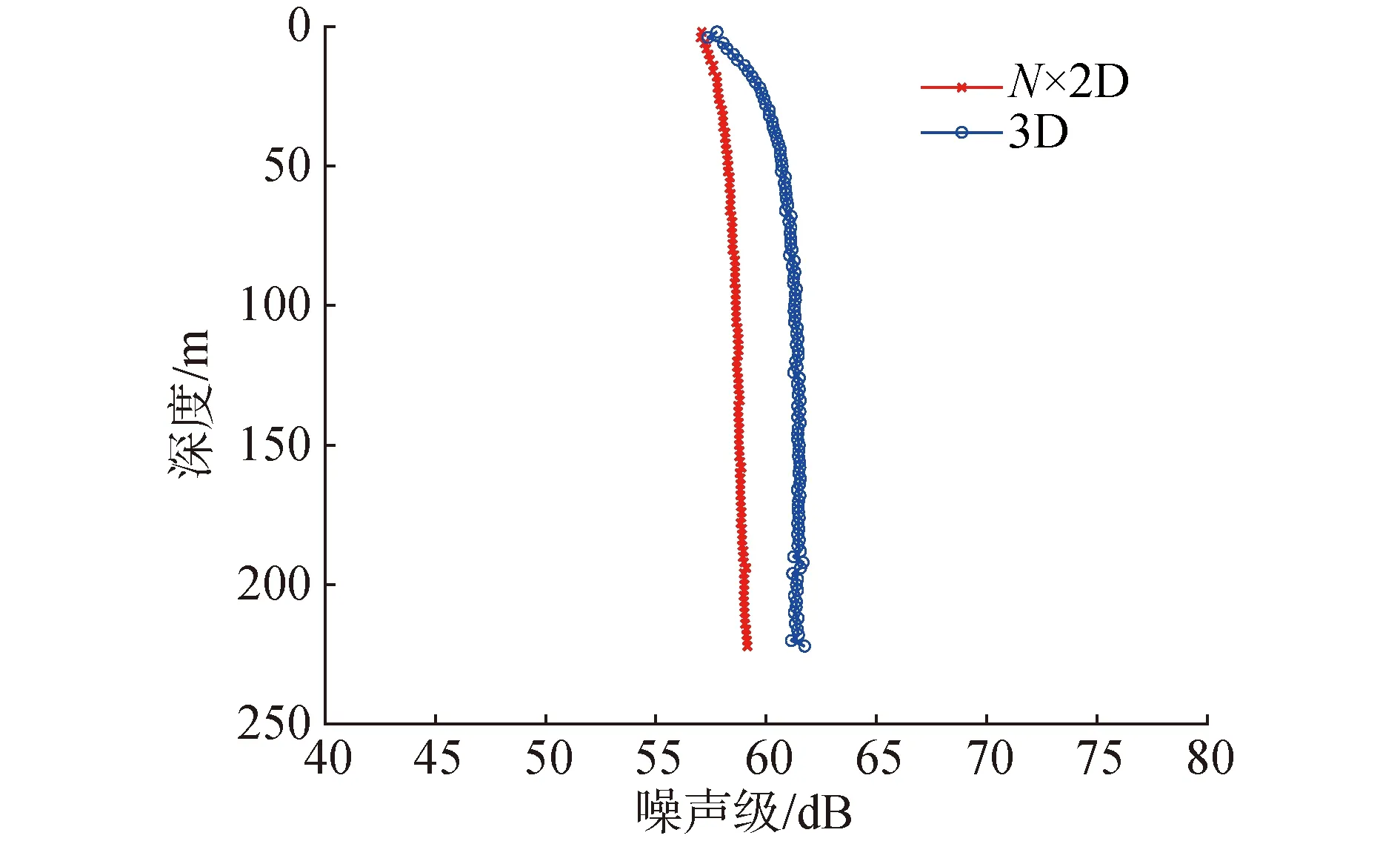
图11 风关噪声级随深度变化Fig.11 Wind-generated noise level vs depth

图13是N×2D和3D算法计算的各方位扇区海洋环境噪声垂直指向性(1 kHz)随方位角变化情况，相邻垂直阵元间隔0.7 m，首阵元深度100 m，末阵元深度121.7 m。接收点的东面方位近距离存在海山/岛礁，方位环境噪声垂直指向性的能量角度结构发生明显的改变，近水平方向噪声凹槽的深度被填补；其他方位的噪声凹槽则比较明显。

归纳起来，上述仿真分析表明：岛礁海域风关海洋环境噪声场和接收点深度、接收点与岛礁的相对位置(包括接收点是否处于岛礁群中间)、岛礁海域海山高度、大小等密切相关。在互不相关风关噪声源均匀分布的假设和负梯度声速剖面条件下，用N×2D和3D模型仿真计算了1 kHz的环境噪声特性，虽然2种算法在不同方位的扇区噪声级存在差异，但趋势相同，且不同深度处，二者全方位的总噪声级差值不超过4 dB。3D算法由于考虑了方位间的耦合，理论上其结果比N×2D结果准确，但在计算时间上，3D算法耗时接近N×2D算法的6倍。

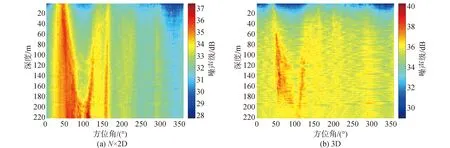
图12 风关噪声级随深度、方位角变化Fig.12 Wind-generated noise level vs depth and azimuth

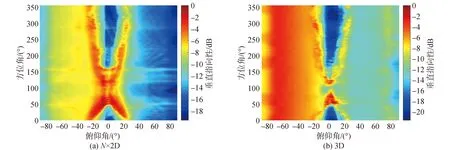
图13 风关噪声垂直指向性随方位角变化Fig.13 Vertical directionality of wind-generated noise vs azimuth

2.5 不同水平方位分区间隔对噪声级的影响

图14是不同的水平方位分区步长(扇区大小)对N×2D和3D这2种算法的噪声级影响，14(a)、(b)分别是上述2个接收点距离海山/岛礁较远和较近算例在水平方位分区步长(扇区)分别是10°、5°和1°的结果。从图中可以看出，在本文采用的海洋环境下，无论是接收点距离海山/岛礁远近，不同的方位分区步长对N×2D算法的计算结果影响非常小，3D算法的噪声级计算结果会随着步长的减小而增大，也就是说对海底地形变化海域，理论上海底地形分辨率越高，水平分区越精细，3D算法的计算结果应该越准确，而水平方位分区越精细，则计算时间就会相应的增加，所以建模需要权衡计算精度和计算时间问题。

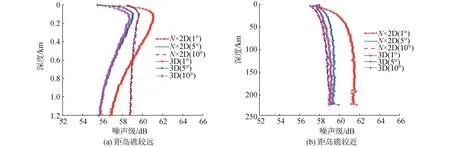
图14 不同方位分区步长对1 kHz风关噪声级的影响Fig.14 Noise levels at 1 kHz vs steps of horizontal azimuth sector

3 结论

1)接收点位于岛礁附近，考虑方位扇区的风关噪声级和垂直指向性，存在海山/岛礁方位扇区的计算值明显不同于平坦海底方位扇区结果，如在海山/岛礁方位扇区的垂直指向性靠近水平方向(小俯仰角)的凹槽深度被填补，而其他方位扇区的噪声凹槽则比较明显。

2)接收点与周边岛礁/海山相距较远时，考虑方位扇区的海洋环境噪声级，海面以下几百米海深内3D算法的结果明显高于N×2D算法，导致几百米海深内全方位总噪声级3D计算值也高于N×2D，在更深的接收深度3D计算值稍低于N×2D；接收点距离海山/岛礁较近时，负梯度声速剖面和海山/岛礁地形致使存在海山/岛礁的方位扇区噪声级均较高，3D计算的各扇区噪声级略高于N×2D；本文算例中2种算法的差值均在4 dB以内。

总体来说，基于风关海洋环境噪声模型的仿真计算结果表明，岛礁海域的风关噪声场和接收点的深度、接收点与岛礁的相对位置(包括接收点是否处于岛礁群中间)、岛礁海域海山的高度和大小等因素密切相关。在随机均匀分布、互不相关风关噪声源假设和负梯度声速剖面条件下，仿真计算1 kHz的风关噪声特性，虽然N×2D近似和3D这2种算法在不同方位的扇区噪声级计算结果存在差异但趋势相近，且不同深度处，二者全方位的总噪声级差值不超过4 dB，理论上本例3D算法结果比N×2D更准确，但相同水平方位分区条件下3D算法耗时约为N×2D算法的6倍，因此在水平方向声速没有剧烈变化情况下，当对计算时间有限制时，可选用N×2D算法来计算风关噪声场特性。