基于遗传-支持向量机的分布式光纤监测矿压时序预测

柴 敬, 王润沛, 雷武林

(1.西安科技大学能源学院, 西安 710054； 2.教育部西部矿井开采与灾害防治重点实验室, 西安 710054)

随着中国工业化的发展,对煤炭的需要也日益增长。煤矿动力灾害现象也与日俱增,为此掌握其机理,减少覆岩变形带来的灾害事故,对其有效的预测和防治成为研究的重要内容[1-2]。其中,用来预测的样本集采用分布式光纤监测相似材料模型试验来获取岩层变形规律数据。分布式光纤的超高精度、可实时监测岩体内部变形等优点成为监测覆岩变形规律的研究热点,结合相似材料模型试验形成研究覆岩变形规律的重要手段之一,柴敬等[3-4]将分布式光纤应用于采动覆岩变形相似材料模型试验中,并提出光纤频移变化度表征矿压等规律。高磊等[5]采用分布式光纤监测斜管,获取斜管应变信息,分析获得基坑深层水平位移变化。朴春德等[6]将分布式光纤应用于杨柳煤矿,成功监测到覆岩变形规律。覆岩变形是一种非常复杂的非线性问题,在工作面开采中及时准确预测其变形引起的矿压规律是预防地质灾害的重要研究问题。对此,部分学者采用神经网络的方法进行来压的预测,贺超峰等[7]、李小永等[8]采用神经网络方法进行来压预测。然而,神经网络虽具有高度的非线性系统、多信息融合的综合预测能力,但其在小样本训练过程中易出现‘维度灾难’和‘过拟合’等问题,需要新的算法替代。因此,支持向量机借助机构风险最小化理论,引入核技巧,保证数据从低维线性不可分映射到高位线性可分,得到全局最优解的能力,成为了研究的新方向。张洋等[9]、郝秦霞等[10]采用支持向量机方法进行顶板来压预测,提高模型泛化能力。此外,王晨晖等[11]、苏晨旭等[12]分别将支持向量机应用于泥石流危险度和滑坡易发性评价预测中。

然而,覆岩变形引起矿压现象是动态演化过程,因此可以采用非线性混沌动力学来构造混沌时间序列预测，其构造的时序预测是解决采矿、岩土、边坡等领域地质灾害的重要手段。其中,陶慧等[13]将其应用于冲击地压时序预测中；董辉等[14]、孙刚等[15]、谢洋洋等[16]将混沌时间序列结合支持向量机应用于滑坡预测、矿压预测、基坑变形预测。引入光纤频移变化度[4],将其看作随开挖距离变化的时间序列,结合支持向量机(support vector machine,SVM)建立时序预测模型。SVM预测模型的泛化能力与其超参数的选取有关。目前为止,借助遗传算法等进行超参数选择有较好效果。其中,曹庆奎等[17]、勒聪聪等[18]使用遗传算法结合支持向量机分别在导水裂隙带和煤层底板破坏程度预测进行研究。

目前,将支持向量机结合光纤数据进行矿压时序预测的研究尚鲜见报道。因此,以宝鸡某煤矿为对象进行相似材料模型制作,获取光纤监测数据,采用遗传-支持向量机对光纤频移变化度进行时序预测。

1 光纤频移表征矿压预测原理

1.1 光纤频移变化度

埋入工作面上覆岩层的光纤,其任意位置的频移变化与该位置的岩层变形相关。定义光纤平均频移变化度为

(1)

式(1)中：Dl为工作面开挖距离l时的光纤平均频移变化度；n为光纤上的采样点的个数；Sj为开挖时的光纤上某一个位置的频移；Sj-1为上一次开挖时的光纤上某个位置对应的频移；j为工作面开挖次数。通过前后两次频移差值来表示该时间段岩体变形程度,即光纤上采样点的任意位置处的频移变化的绝对值可以表示该位置岩层在某一段时间内的变形大小。其曲线会随开挖次数出现突峰,因此可以作为上覆岩层初次来压或周期来压的判断指标。

1.2 支持向量机时序回归原理

根据Takens理论进行相空间重构,对光纤频移变化度数据集进行一维投影,将光纤频移变化度作为随开挖距离变化的时间序列x=[xi],光纤频移变化度构成的时间序列数据集为{x1,x2,…,xi},xi是开挖一次的光线频移变化度,i=1,2,…,n。选取嵌入维数m和延迟时间τ是相空间重构的关键,这里嵌入维数采用预测误差最小法进行确定,延迟时间采用互信息法进行确定。由相空间重构后的构成的学习样本集为Y(m)=f[xi,xi+1,…,xi+(m-1)τ],其中i=1,2，…,n-1-(m-1)τ,共n-1-(m-1)τ个样本。已知上一开挖光纤频移变化度xi预测下一次开挖光线频移变化度xi+1,通过支持向量机学习到一个函数f(x),使得样本以外的X通过f(x)的映射找到对应的Y,且使真实值与Y尽可能地接近。将m作为输入特征建立训练样本,X和Y对应关系为

(2)

通过φ(xi)将样本映射到高维空间,建立支持向量机回归目标函数为

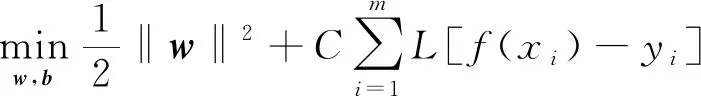
(3)

式(3)中：f(xi)=wφ(xi)+b为需要找的回归函数；C为正则化系数；L为不敏感损失函数；w为权值；b为阈值；yi为真实值。

引入松弛变量

和不敏感参数ε,将式(3)转化成目标极小化函数,即

(4)

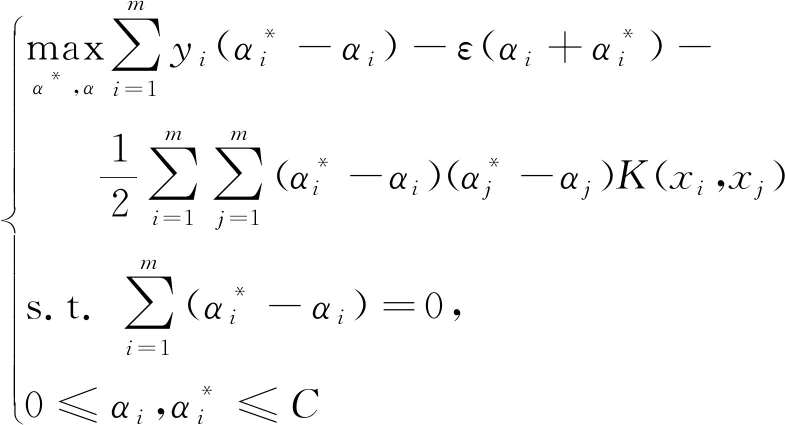
(5)

通过式(5)推导得SVR回归函数为

(6)

式(6)中：K(xi,xj)=φ(xi)Tφ(xj)是SVR的核函数。

1.3 GA-SVM时序回归模型

不同的核函数具有不同的核函数参数,无论样本大小、维数多少,径向基核函数均表现效果好,且σ是高斯径向基核函数唯一参数,为核宽度易于实现。经试验效果,高斯径向基核函数效果最好,因此,选其作为模型核函数，即

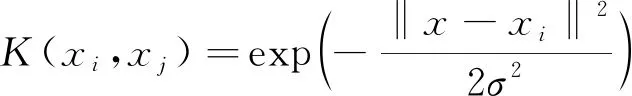
(7)

选取高斯径向基作为核函数的SVR模型,其预测精度的高低主要取决于模型惩罚因子C和核函数参数σ的选择。人工经验选取会造成误差,需要科学的选取方法。因此,引入遗传算法通优化参数,选取最优SVR预测模型。编程方式采用华南理工大学开发的Geatpy遗传算法工具箱和 Python语言。使用编程语言进行建模的程序流程如图1所示。

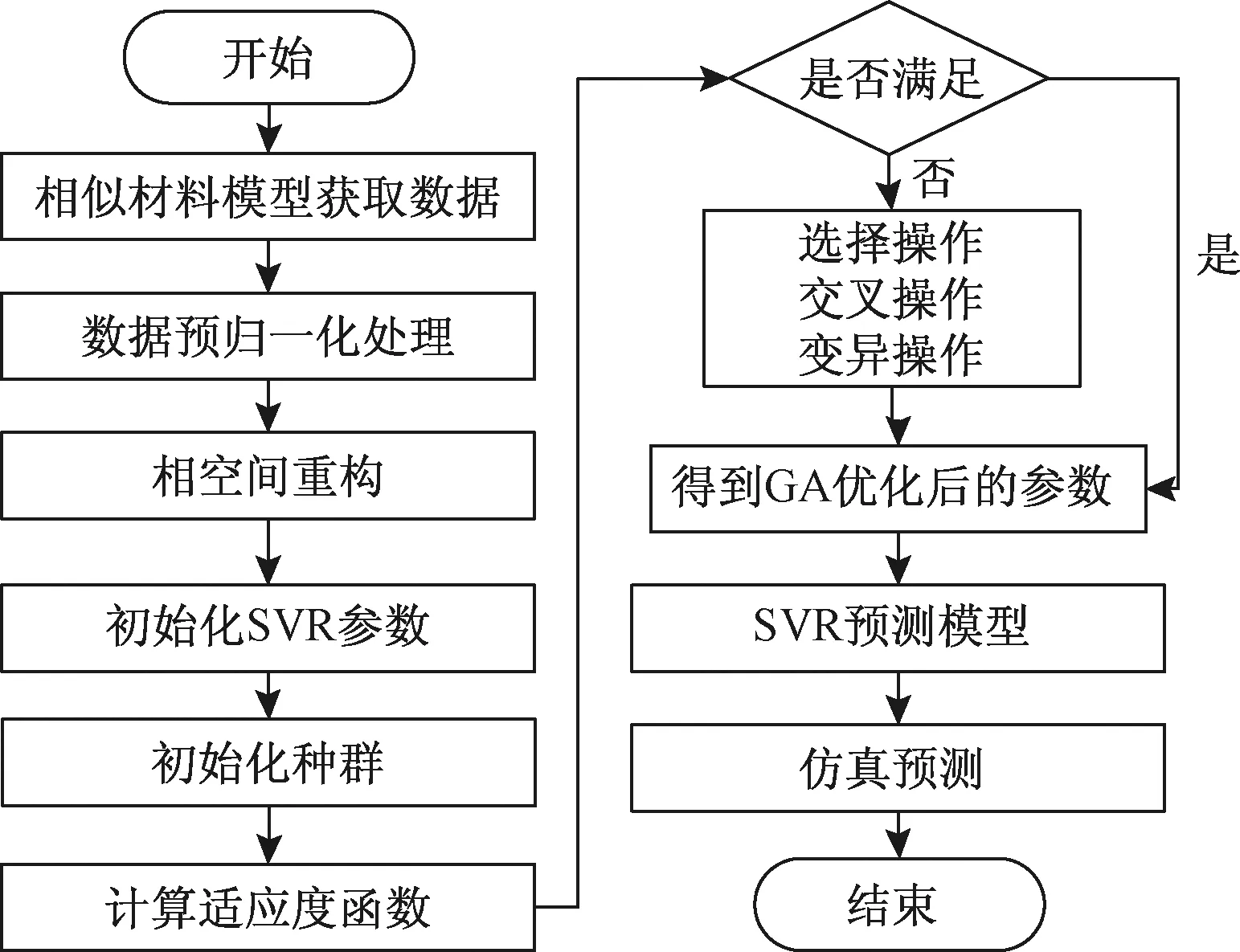
图1 SVR矿压时序预测模型流程

2 基于SVR的矿压时序预测试验应用

2.1 相似材料模型试验获取数据

以宝鸡某矿区地质柱状及其物理力学参数为对象,制作尺寸为3 000 mm×200 mm×2 000 mm(长×宽×高)的二维采场覆岩模型,其中,模型几何相似比为1∶100,模型高度为1 290 mm,其中上覆岩层厚度为1 180 mm,煤层厚度为50 mm,地板厚度为60 mm。总共开挖60步,共计2 400 mm。

分布式光纤测试系统选用日本Neubrex基于PPP-BOTDA技术研发的新一代光纤传感系统,如图2所示。在模型铺装过程中,埋设3根垂直光纤,记为V1、V2、V3，分别位于距离开切眼600、1 200、1 800 mm模型尺寸。开挖工作面位置和追至光纤布置位置如图3所示。

图2 NBX-6055分布式光纤测量仪

图3 相似材料模型试验

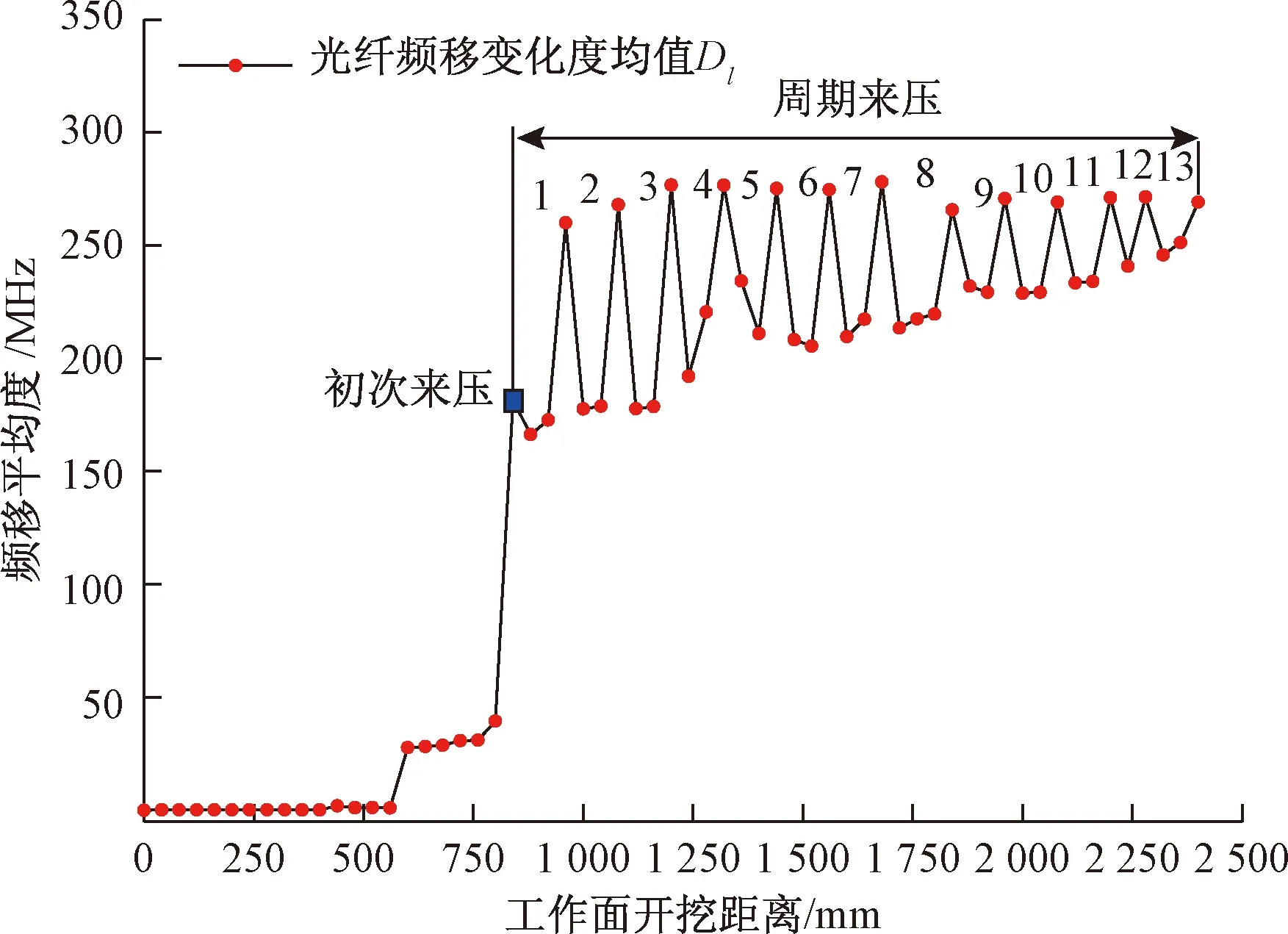
图4 光纤表征矿压规律示意图

经模型试验测得光纤频移值结合式(1)可知,3根光纤Dl求均值可以得到来压规律分为1次初次来压和13次周期来压。如图4所示,根据光纤频移变化度Dl得出了工作面来压的基本表现形式。整个过程共出现14次光纤频移变化度“尖峰”,在工作面开挖840 mm时首次出现尖峰,并在960、1 080、1 200、1 320、1 440、1 560、1 680、1 840、1 960、2 080、2 200、2 280、2 400 mm处出现频移尖峰。以此数据为样本集,将样本集按4∶1分割,前48次开挖作为训练样本,后12次开挖作为测试样本。训练不同的预测模型,并对模型进行评估,选取最优模型。

2.2 数据预处理及模型性能指标

通过上述实验得到60次光线频移变化度。在对数据进行均一化处理后,需进一步研究模型性能,保持数据训练样本和测试样本不变的条件下,对SVR和BP神经网络进行矿压数据预测建模和测试分析。通常使用平均绝对误差MAE、均方误差MSE和决定系数R2这3种指标作为回归问题的评估指标。

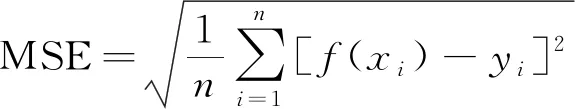
(8)

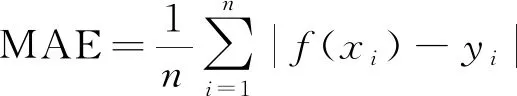
(9)

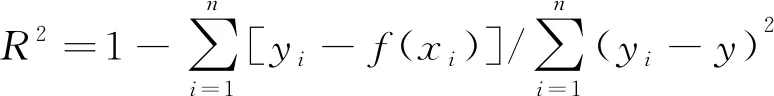
(10)

3 结果与分析

3.1 参数确定及分析对比

根据图1流程图所示,首先确定延迟时间为1,嵌入维数为3。再利用GA遗传算法对支持向量机参数C、σ进行寻优,其中遗传算法初始化参数设定为：种群个数为20,最大进化代数200,参数C的变化范围为[0,100],参数σ的变化范围为[0,1 000]。经过54次迭代后达到最优,在100次迭代后终止。经过优化后确定,C=11.625,σ=1.725，不敏感系数取程序库默认值ε=0.1,参数寻优过程如图5所示。

将参数代入SVR模型中对样本进行训练,使用相同训练样本集对传统SVR和神经网络进行训练,其中传统支持向量机参数采用程序默认数值,对于BP神经网络来说,选取两层隐含层,神经元个数为(5,2),输出层为回归函数进行拟合。

上述3种模型测试结果如图6所示,从图6中可以看出,取后12次开挖产生的频移变化度作为测试集。共出现5次光纤频移变化度“尖峰”,因此共计出现5次来压。从矿压时列数据的开挖预测结果,可以看出神经网络在前8次开挖过程中正确预测出2次来压,之后的预测数值几乎不变,说明其出现了“过拟合”现象。传统SVM整体趋势效果不错,正确预测出4次来压,但在第4、8次开挖出现较大误差。GA-SVM预测性能效果好,整体趋势吻合无较大误差,且12次开挖过程中成果预测出5次周期来压。

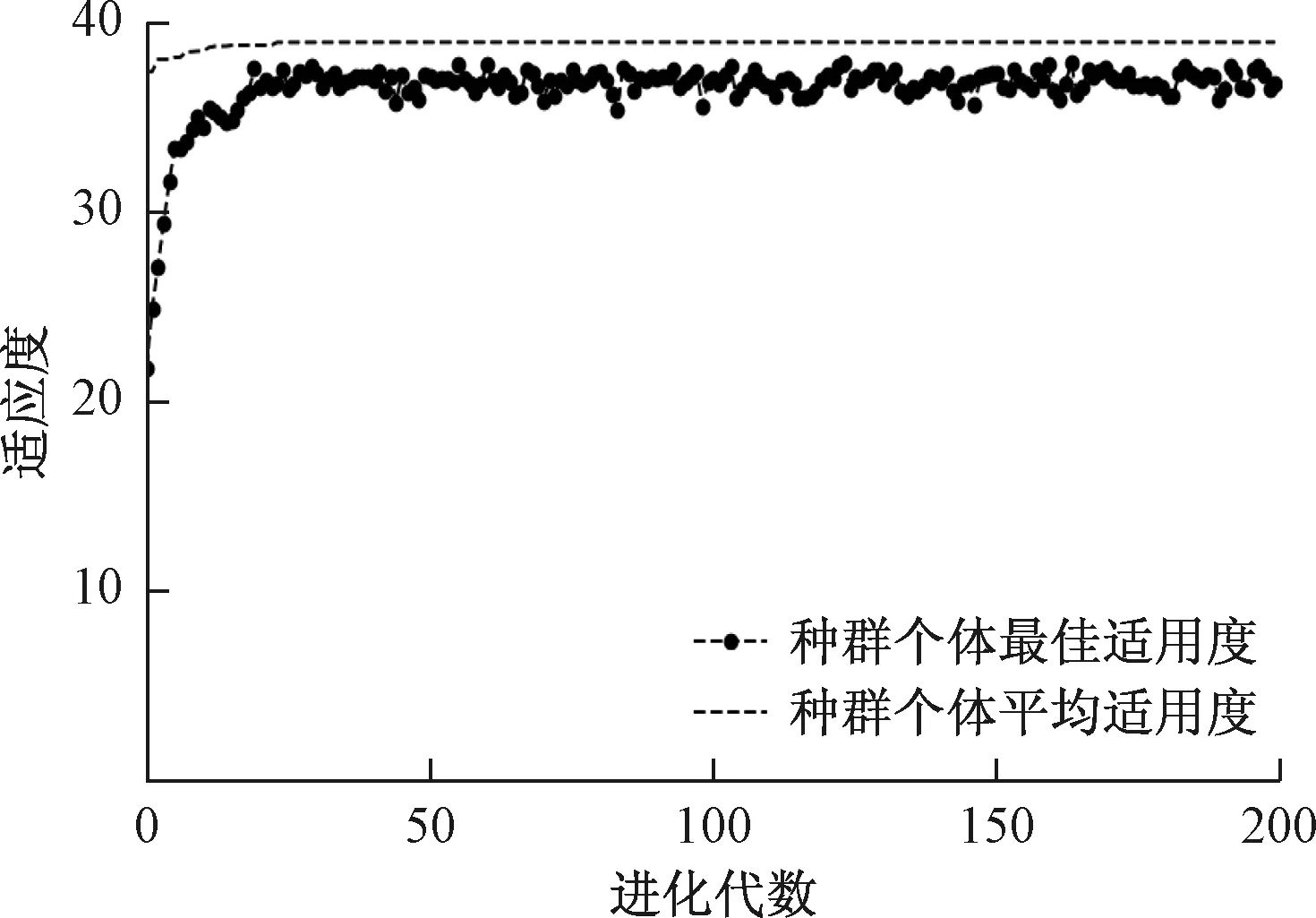
图5 GA-SVM参数寻优过程

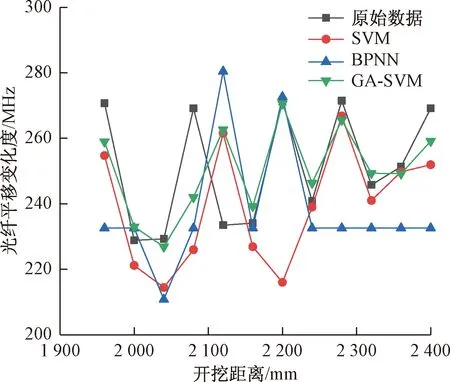
图6 光纤频移变化度实测值和预测值关系

3.2 模型性能对比

为了进一步对比分析,如表1所示。其中均方误差MSE和平均绝对误差MAE的数值越接近0模型表现越好。R2反映了对信息拟合度的好坏,其数值越接近1模型表现越好。由表1可知,在测试阶段BP神经网络测试样本的MSE相对于训练样本增多,决定系数在减小,说明神经网络模型存在过拟合显现,在测试集上由较大误差。传统SVR在训练集和测试集表现效果较好,但其超参数通过人工经验选取,没有很好的科学依据,会造成一定程度的误差,采用GA-SVR,其决定系数接近1,MSE接近0,与训练阶段差异较小,说明具有较强泛化能力。

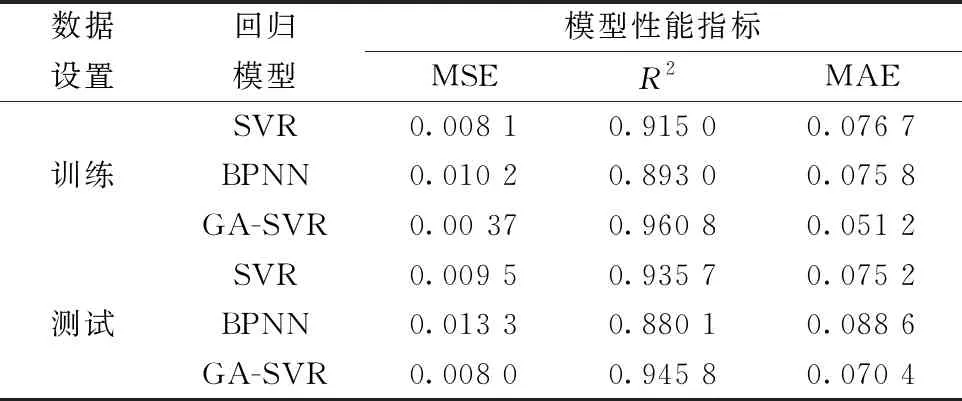
表1 不同模型性能指标对比

4 结论

(1)引入遗传算法优化SVR参数和相空间重构方法,结合分布式光纤传感技术,提出基于GA-SVR的分布式光纤监测矿压数据的时序预测方法。

(2)通过分布式光纤传感器技术监测到光线频移变化度,并通过二维平面模型试验进行验证,建立光纤监测系统,并用预测结果与BPNN、传统SVM方法进行分析比较。验证GA-SVR在煤矿开采过程中预测矿压显现是一种可行、有效和准确的方法。

(3)在模型性能上BPNN模型在其训练样本上表现良好,但在测试样本上易出现“过拟合”现象引起预测误差。GA-SVR其拥有最佳的训练结果,相对于传统SVR在选取超参数上更加科学,模型的预测精度更高。说明参数选取对SVR精度具有重要影响,并且其在处理模型试验小样本、非线性数据性能要好于BPNN模型。因此,GA-SVR在矿压预测中具有很高的实际推广价值。