基于改进天牛群算法优化的BP神经网络的入侵检测
王振东, 曾 勇, 王俊岭, 胡中栋
(江西理工大学信息工程学院, 赣州 341000)
随着计算机技术及网络的不断发展进步,网络安全性受到越来越多的重视。然而网络中存在着量大且复杂的攻击行为,这些攻击已然成为网络及信息安全的主要威胁。入侵检测[1]作为防火墙之后的第二道防线,具有积极主动且动态的防御能力,有效地弥补了传统安全技术的不足。一般情况下,入侵检测可以分为异常和误用两种不同的检测类型。误用检测是依据已有的攻击数据信息特征与主机或网络中的数据进行匹配,如果匹配的结果相符合,则被定义为异常行为,这种检测方式只能检测样本数据库中已存在的网络攻击类型。异常检测方法是先在样本数据库中建立具有正常行为轨迹的基本特征,再将所有偏离或不符合正常轨迹的行为都视为入侵行为。
当前对于入侵检测技术的研究主要集中在3个方面,分别是基于机器学习的入侵检测、基于数据挖掘的入侵检测和基于神经网络的入侵检测。尤其是神经网络具有多数据并行计算、良好的自适应学习能力、高速的寻优能力及较强的抗干扰性能,并能够处理有失真及不完整数据信息等特性,非常适合从庞大网络中复杂、高速且量大的数据中识别入侵数据。杨雅辉等[2]提出了具有增量式分层自组织映射(growing hierarchical self-organizing maps,GHSOM)的算法模型结构,该结构能够保留已学习过的知识,再对现实网络流量中新出现的攻击进行增量式的学习。该方法使得神经网络算法模型具有良好的动态自适应性,对于新型的网络攻击类型仍能够保持较好的检测率。苏洁等[3]利用DS(dempster/shafer)证据理论提出了一种基于GHSOM的入侵检测模型。该模型能够在入侵检测过程中通过动态控制网络子网的拓展速度,从而提升网络子网的动态适应性。该方法在网络流量数据有噪声的情况下也能够保持较好的检测率,但没有评估到现实网络中由于网络数据随机性这一情况的出现及实际网络数据会出现短时间膨胀对于检测率的影响。
BP(back propagation)神经网络[4]是一种严格按照误差逆向传播及训练的多层前馈神经网络,是目前应用最为广泛的神经网络。由于BP神经网络模型具备较强的自学习能力,当应用于入侵检测时BP神经网络不仅能检测网络数据中存在的已知攻击,对未知的网络攻击类型也具有一定的检测效果。但是,BP神经网络的权值阈值及学习率等参数选取时具有随机性较大等特点,容易导致网络出现收敛速度慢、BP算法易陷入局部最优等问题[5]。
对此,研究人员提出了相应的改进策略,周爱武等[6]采用模拟退火算法寻找更优化的样本子集,有效地加快了网络收敛速度及缩短了学习时间。梁辰等[7]用综合主成分分析(principal component analysis,PCA)和附加动量法,对数据特征选择和对网络权值的修正,使得在网络样本过大时收敛性能有保证。Sun[8]利用动量式粒子群算法及自适应度训练优化算法,通过改进BP网络,提出了一种较为新型的算法结构模型MLPSO-BP,仿真实验结果表明,该算法模型能达到较高的检测率。Cui等[9]调整相关规则检测网络中的异常流量,比起传统的BP网络模型,能够有效地降低误报率增量及总误差。Qiu等[10]提出了一种基于BP神经网络的变异粒子群算法(mutation-particle swarm optimization,MPSO)和MPSO优化算法的改进算法,并提出了基于神经网络的MPSO_BP:MPBIDS入侵检测模型,该模型有很强的重用及扩展能力,能及时监控整个庞大的网段、可以处理大量的网络数据、具有较强的自主学习能力和提高入侵样本检测率等优点。
与传统的BP网络算法相比,使用遗传算法、蚁群算法和PSO算法等群智能优化算法优化的BP神经网络,确实能够在一定程度上加快BP神经网络训练及学习的收敛速度,减小该算法陷入局部最优的可能性。但是对于复杂较高维问题时,传统智能优化算法过早收敛的特性并不能保证模型收敛到最优值[11],且一般的智能算法所优化的BP神经网络,通常情况下算法表现为结构相对比较复杂,且初始参数较多,加大了BP神经网络算法的复杂性。
天牛须算法(beetle antennae search algorithm,BAS)2017年由Jiang等[12]提出,核心思想是模仿生物界里具有感知触须的天牛寻找食物过程而演变而成的智能搜索算法。该算法具体方法是使用天牛触须来感知并确定出天牛下一步需要移动的方位,天牛触须灵敏的感知能力能够有效地减小各天牛进行无目的且随机的无规则转移的概率,进而直接提升了该算法的收敛速度。BAS具有结构简单、初始及可变参数较少等其他智能算法不具有的优点。然而,原始的BAS也有其局限性,只能实现单体搜索,意味着在较高维(一般大于4)的空间中搜索解时易陷入局部最优解,无法跳出。因此,在现有并在研究的群体智能优化算法基础上,提出天牛群算法(beetle swarm optimization,BSO)。该算法的本质是通过将天牛个体独自搜索的方式变化为群体共同搜索的方式,以此加强天牛个体间的联系,并且引入动态的步长策略让每个天牛个体能够实现可变步长的不规则移动,不仅保留BAS初始及可变参数少、容易实现的优点,还避免了BAS算法在多维甚至高维问题上容易陷入局部极值、精度较低等缺陷。最后,对BSO再进行改进,并将改进的BSO应用于BP神经网络权值和阈值的优化,提升BP神经网络对入侵网络数据的检测性能。实验阶段对BP神经网络、GWOBP(grey wolf optimizer-back propagation)、PSOBP(particle swarm optimization-back propagation)进行了比较,并在网络入侵数据集NSL-KDD上对算法优化后的BP神经网络模型分别进行了仿真实验验证。
1 BP神经网络
BP神经网络是一种广泛应用于各项研究的多层前向型神经网络。BP神经网络是由3个部分组成,分别是数据输入层、作为计算的隐藏层和结果输出层。BP神经网络主要包括输入数据信号的正向传播和结果误差反向传播两个过程。
(1)正向传播过程。信号通过神经网络输入层输入,随后各隐藏层的神经元对其进行处理,最后传入神经网络的输出层,得到信号处理的实际输出值,若预测值与真实值之间的误差未达到BP神经网络所设定的精度,则将该误差转入反向传播的过程。
(2)反向传播过程。反向传播过程是将预测值与真实值之间的误差通过BP神经网络隐藏层向输入层进行逆向传导,在这个过程中利用BP神经网络的误差分配机制将误差分配给各个神经元,并沿着误差函数下降最快的方向调整BP神经网络的权值和阈值,然后用该过程更新后的权值和阈值进行正向传播。进行反复的正向和反向传播过程,直到训练的BP神经网络输出误差满足所设定的精度要求,或达到预先设定的学习次数为止,就是BP神经网络的学习过程。图1所示是一个典型的三层BP神经网络结构。
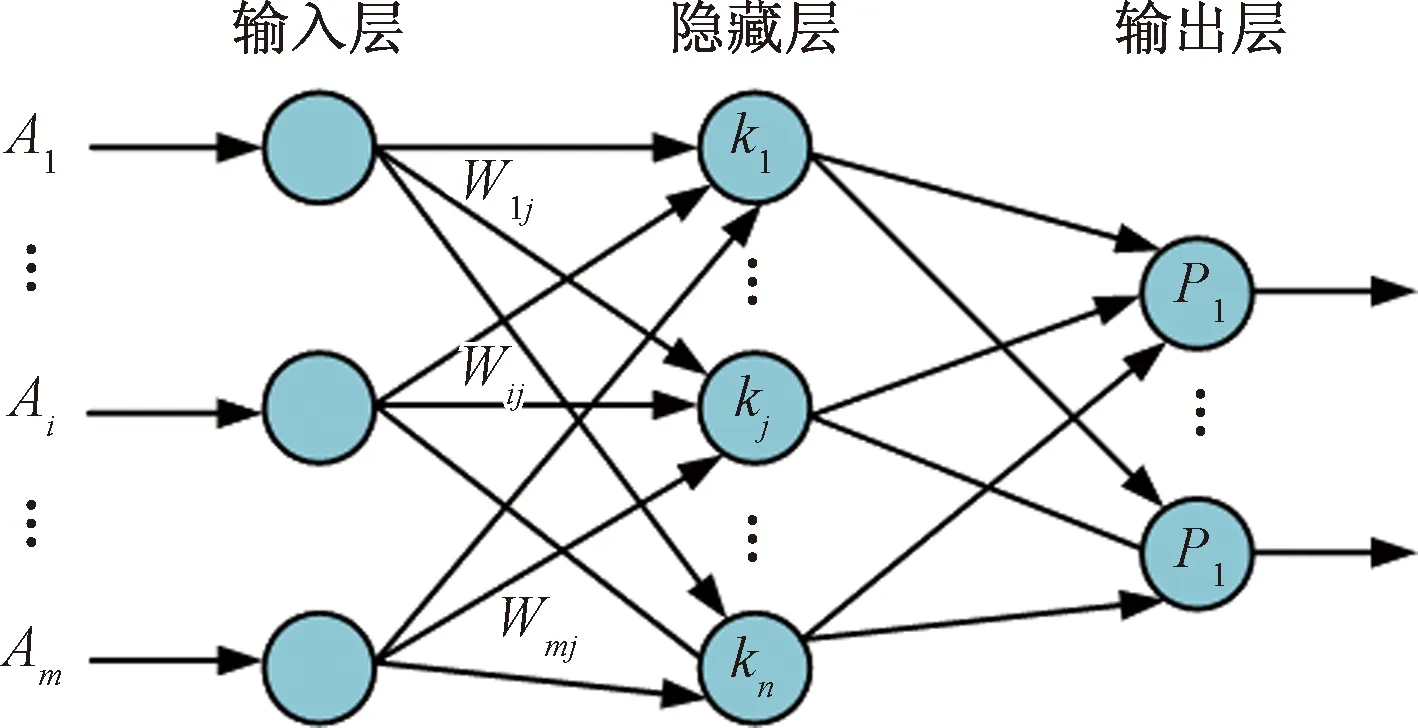
图1 典型三层BP神经网络结构
图1中A1,A2,…,Ai,…,Am为输入层神经元的输入值,W1j,W2j,…,Wij,…,Wmj为输入层的节点与隐藏层的第j个节点之间的网络权重,k1,k2,…,kj,…,kn为隐藏层输入,P1,P2,…,Pl为输出层输出。BP神经网络算法步骤如下。
步骤1初始化。首先将BP神经网络的权重及阈值正态分布随机初始化至-1~1,确保每个神经网络单元都有一个初始阈值。
步骤2正向传播过程。将已进行数据预处理数据样本输入BP神经网络进行训练,然后利用各层的输出公式计算该BP神经网络中各层的输出值。
(1)该过程的隐藏层输出的计算公式为
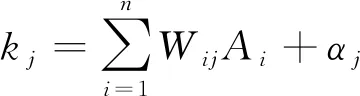
(1)
式(1)中:αj为隐藏层第j个神经元的阈值。
(2)利用BP神经网络的激活函数计算隐藏层各神经元的实际输出值。隐藏层的实际输出计算公式为
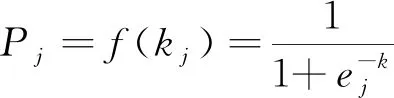
(2)
式(2)中:f为sigmoid激活函数。
(3)将隐藏层各神经元计算得到的结果进行输出。
步骤3依据误差反向传播及误差分配机制,最后用梯度下降算法对BP神经网络权值阈值进行反向更新取值。
(1)根据式(3)计算输出层的误差:
Errl=Pl(1-Pl)(Tl-Pl)
(3)
式(3)中:Pl为预测值;Tl为真实值。
(2)根据式(4)计算隐藏层误差:
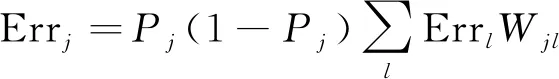
(4)
式(4)中:Pj为BP神经网络隐藏层的输出值;Errj为隐藏层的误差;Errl为输出层的误差;Wjl为神经网络隐藏层的第j个神经元与输出层第l个神经元之间的权重。
(3)按照式(5)和式(6)更新权值和阈值:
Wij=Wij+ΔWij=Wij+(O)ErrjPi
(5)
αj=αj+Δαj=αj+(O)Errj
(6)
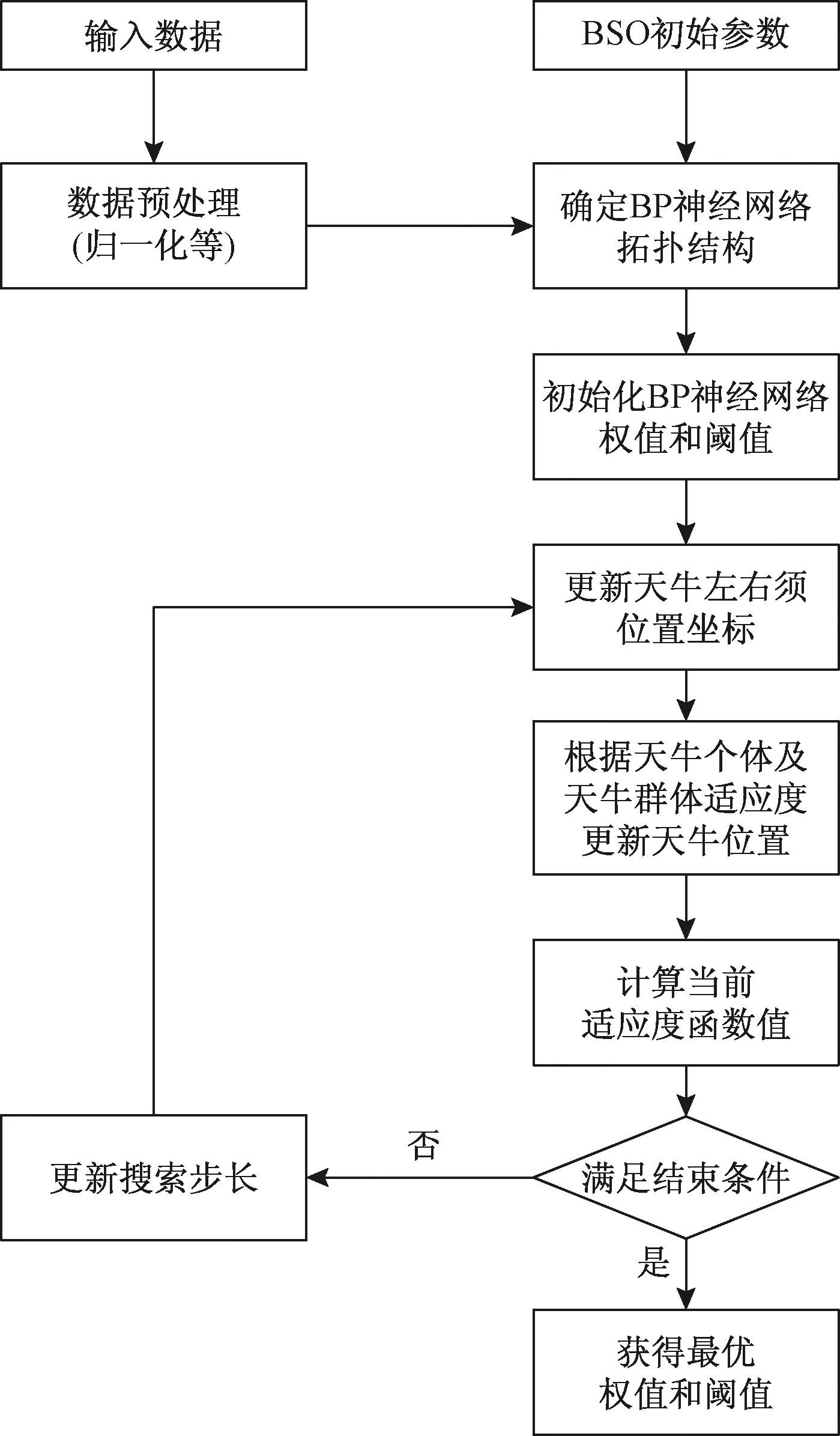
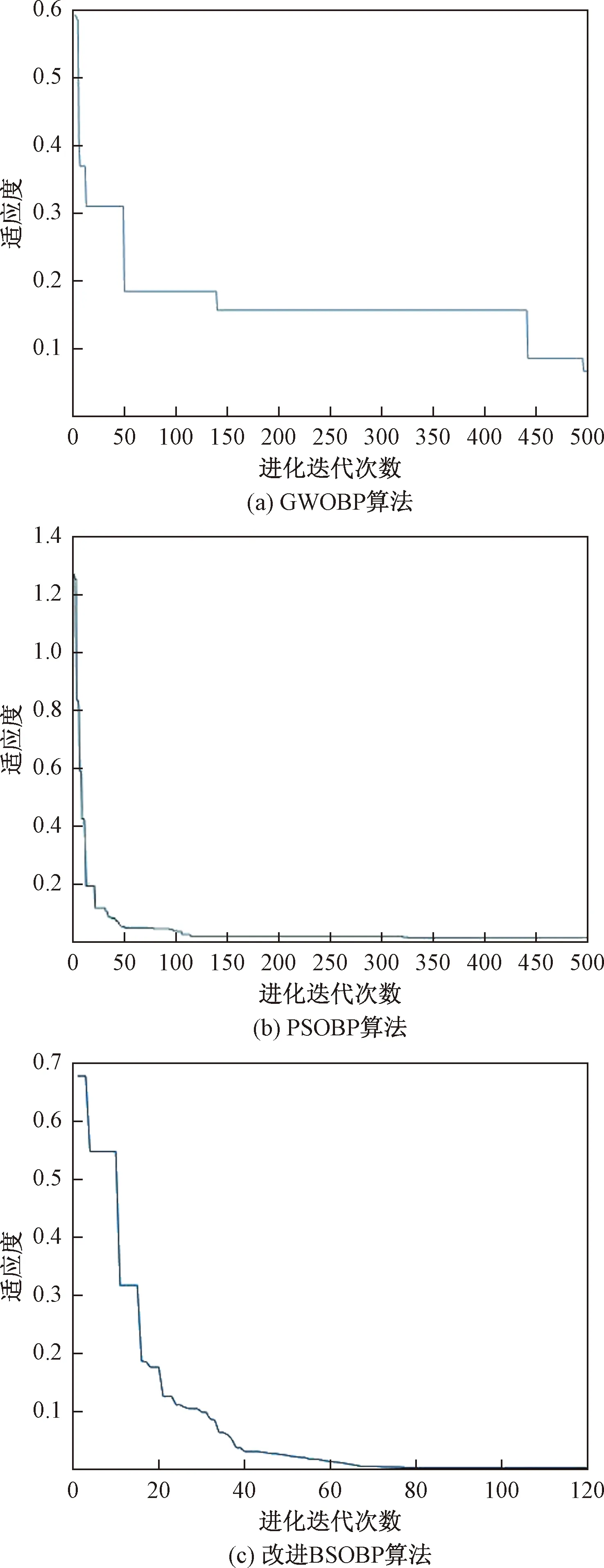
式中:O为学习率,取值范围是0 步骤4不停重复上述的步骤2、步骤3,直到训练BP神经网络所输出的误差值满足所预定的精度要求,或达到预先设定的学习次数为止,结束算法。 天牛须搜索算法(BAS)是启发于天牛寻找食物的过程,可用于对目标函数进行优化的新技术,其生物原理为:当天牛个体寻找食物时,开始时并不知道食物的具体位置在哪里,只能感知到空气中食物气味浓度的强弱,使用感知能力来觅食。每个天牛个体通过左右两只长触须感受当前环境中的食物气味浓度大小,若右须感知浓度比左边触须大,那天牛下一步将会向右边飞,反之则向左边飞。根据这一简单的觅食搜寻原理,天牛个体便可以有效且快速地寻找到食物的具体位置。与遗传算法、粒子群算法等类似的是,BAS并不需要提前知道函数的具体表现形式以及梯度等各类信息,就可以轻易实现自动寻优的这一过程,而且其天牛个体仅为一个,寻优速度显著提高。BAS模型建立的步骤如下。 求解D维模型优化问题时,天牛个体可以由质心、左须及右须3个点来代表。 (1)对天牛须的朝向作随机向量并做归一化处理得: (7) 式(7)中:rands为随机函数;D表示空间维度。 (2)创建天牛左右须与质心之间的坐标关系 (8) 式(8)中:xrs表示在第s次迭代时该天牛右须的位置坐标;xls表示在第s次迭代时该天牛左须的位置坐标;xs表示在第s次迭代时该天牛的质心坐标;L表示左右两须之间的距离。 (3)根据适应度函数来确定该天牛左右须的气味强度,即f(xr)和f(xl)的强度,f函数为适应度函数。 (4)天牛位置迭代更新方法: (9) β(s+1)=μβ(s) (10) 式中:β(s)表示在第s次迭代时的步长;f(xls) 和f(xrs)分别代表第s次迭代时该天牛左右须气味强度;sign()为符号函数;μ为步长因子,一般取0.95。若右须的适应度大于左须,sign()取1,天牛往右须方向以步长β(s)移动,反之,往左须方向移动。 2.2.1 初始种群 文献[13]表明,在群智能搜索算法中,收敛性很大程度地受初始群体分布的影响。所以在各类群智能搜索算法初始群体分布得越为均匀,意味其初始群体中包含着越多有意义的有效信息,往往能使智能搜索算法更快速地收敛到优的解;反之,会对算法性能产生影响[14]。因此采用混沌序列搜索的方式来产生实验所需要的初始天牛群体,混沌序列能使产生的天牛群体具有遍历性、规律性及内随机性等特点,能够使初始种群分布更加均匀,即在一定程度上提升了群智能算法的搜索寻优效率[15]。目前,大部分研究者使用Logistic映射[16]来产生初始混沌序列,然而需要更为均匀的初始种群,可是Logistic映射对具有初始值的混沌序列要求较高且较为敏感,故该映射不适合产生均匀性较好的混沌初始序列。单梁等[17]通过大量的仿真实验直接证明了Tent映射要比Logistic映射在闭区间[-1,1]上产生的混沌初始序列分布得更为均匀。因此,采用式(11)所示的Tent映射来产生相对较为均匀的初始天牛群体: (11) 2.2.2 感知因子及学习策略 由于BAS算法中存在天牛个体搜索寻优的能力范围有限的缺点。导致天牛个体要从当前搜索的局部区域向临近区域搜索进行寻优转移并不容易,从而直接降低了该算法的收敛性能。虽然群体搜索算法能扩大搜索寻优的范围且明显优于个体搜索算法[18],但各天牛群体间的天牛个体之间严重缺乏实时信息的交流及信息数据的反馈,并不能高效快速地解决收敛问题。为此,引入可变的感知因子及具有导向性的学习策略。各天牛群体中的每个天牛在用触须感知当前的移动方位时,还要通过学习并比较历史天牛群体之间的寻优值,以此来保证天牛群体中独立的天牛个体向天牛群体中最优的个体方向移动靠近。这种具有指导作用的导向策略够有效减少该算法在多维及较高维的搜索空间中的收敛时间。因此,天牛个体的移动寻优既受到自身感知判断的影响,又受到群体的导向。 综上所述,根据式(7)、式(8)可以确定天牛须朝向及左右触须的具体位置,其中参数L代表两须之间的距离值,该值越大,则表示天牛个体越大,其触角感知范围便越大。所以,天牛个体位置的更新方法为 (12) (13) 2.2.3 改进BSO-BP神经网络模型的建立 利用天牛群搜索算法寻找确立BP神经网络的最优初始权值和阈值,并将该最优值应用于设定好参数的BP神经网络中,从而设计出最终的BP神经网络训练模型。该模型可以很好地克服原始BP神经网络训练及测试稳定性较差、算法易陷入局部最优等缺点。模型建立方法如下。 (1)定义空间维度D,设该模型结构为A-B-1,A为BP神经网络输入层神经元个数,B为隐含层神经元个数,1是输出层神经元个数,则计算搜索空间维度D=AB+B1+B+1。 (2)感知因子yt的设置。感知因子yt用来控制天牛的区域搜索的能力,初始步长应设置的大些,使之足以覆盖当前的搜索区域而不至于陷入局部极小值,采用导向性的学习策略,向天牛群体最优学习,即式(13)所示。 (3)确定适应度函数。以测试数据的误差和作为适应度评价函数,用于推进对空间区域的搜索。函数为 (14) (4)天牛群初始化。采用Tent映射来产生较为均匀的天牛初始群体,并创建每个天牛须朝向的随机向量。 (5)评价。根据适应度函数式(14)计算在初始位置时的适应度函数值。 (6)天牛左右须位置的更新。根据式(8)更新天牛须的位置坐标。 (8)迭代更新控制。判断适应度函数值是否达到设定的精度(取值为0.001)或迭代进行到最大次数(500代),如果满足条件要求则转步骤(9),否则,返回到步骤(6)继续进行迭代。 (9)最优解生成。当算法停止迭代时,即适应度函数值达到设定的精度0.001或迭代达到500代时,得到的解为BP网络训练的最优解,即BP神经网络的最优初始权值和阈值。再将上述得到的最优解代入BP神经网络中进行二次训练及学习,形成最终的入侵检测分类模型。 综上所述,给出改进BSO-BP入侵检测分类模型的具体流程,如图2所示。 图2 改进BSO优化BP神经网络流程 先把网络流量数据进行预处理,然后用改进天牛群算法优化的BP神经网络和传统的BP神经网络、粒子群算法优化的BP神经网络及灰狼算法优化的BP神经网络做了收敛速度对比和检测正确率及误报率对比2个实验。 为了评估本文模型及算法的有效性,实验使用已经去噪处理且比较理想的公共数据集NSL-KDD,原始数据来自MIT林肯实验室收集的美国空军模拟网的流量监控数据,后来被哥伦比亚大学等整理成规范的公共数据集KDD99[19]。大约共有5×106条网络数据信息,39种网络攻击类型,每一条网络数据都有41个特征属性和1个类标识。该数据集中包含了1种正常的标识类型normal和4种异常的标识类型Dos、Probing、U2R、R2L,其中4种异常共含有22种攻击类型,如表1所示。 表1 NSL-KDD入侵检测实验数据标识类型 与此同时,为了能够进行统一的度量,对原始数据样本进行归一化处理,使得处理后的网络流量数据均匀分布在区间[-1,1]内,使用的是mapminmax函数。 实验环境为windows7 64位操作系统,处理器Intel(R)Core(TM)i5-6500 CPU 3.20GHz,安装内存(RAM)8.00 GB。仿真环境是MATLAB R2016a。仿真实验中抽取3组样本数据(记为S1、S2、S3)进行入侵测试,每组样本数据中共包含2 400条网络流量事件记录,都是由2 000条正常网络流量事件记录和400条入侵行为记录组成。在每个样本数据中的攻击类型数目不同,能够有效对比4种算法检测不同攻击类型的功能。详细样本数据如表2所示。 表2 含有2 400条记录的样本数据 仿真测试中使用传统的BP神经网络算法及以下3种BP神经网络,包括粒子群算法优化的BP神经网络、灰狼算法优化的BP神经网络和本文改进的天牛群算法优化的BP神经网络采用相同的网络流量样本数据进行测试。在入侵检测实验过程中,采用检测率(DR),误报率(FPR)两项指标作为对算法检测能力的评价,指标定义为 (15) (16) 式中:TP表示被正确识别的各类网络流量样本个数;FN为未检测出的各类网络流量样本个数;FP为被误当作检测出的属于各类网络流量样本的个数。 4种算法中,使用相同的BP网络拓扑结构,即41-30-5,用2 100条数据进行测试,300条数据进行预测,每种算法均在仿真环境下进行多次实验,取各次实验结果的平均值,其中仿真实验结果如表3所示。 表3 4种算法仿真实验结果 从表3的实验数据相比较得出,用具有动态性感知因子、具有指导作用的导向性学习策略改进的BSO算法优化的BP神经网络参数而提出的BSOBP优化神经网络算法,与BP算法、GWOBP算法及PSOBP算法相比,在同一实验环境条件下,提出的改进BSOBP算法使得BP网络模型的入侵误报率得到明显降低,而入侵检测率有显著提高。仿真实验数据说明,改进BSO算法能够有效提升BP神经网络模型对网络流量数据的检测性能,并降低误报率。用图3表示表3中的实验数据,能够更加直观地说明及比较仿真实验结果。 图3 4种算法的仿真实验结果 4种攻击类型在网络流量数据样本中的平均检测率和误报率仿真结果如表4 所示,由于R2L和U2R两种网络攻击类型的网络流量数据在总体及样本数据量中相对其他攻击类型较小,故容易造成错判,导致仿真实验中对于R2L和U2R两种攻击类型的检测率相对比较低,但改进的BSOBP算法仍能较好地检测这两类异常数据,检测率分别是63.64%、68.75%,虽相比BP算法,GWOBP算法及PSOBP算法对R2L和U2R的检测率有所提高,但检测率均低于60%;4种算法对于DOS和Probing两种网络攻击类型的检测率是相对较高的,改进BSOBP算法的入侵检测率分别高达95.29%、91.47%,GWOBP算法及PSOBP算法相比BP算法检测率更高,但检测率均未达到90%;相比4种攻击在各个算法优化的入侵检测模型中的误报率,相比其他算法,特别是BP算法,改进BSOBP算法模型对DOS的攻击的误报率降低了高达5.4%,而GWOBP算法和PSOBP算法虽相比BP算法对误报率有所降低,但其中GWOBP算法降低误报率幅度最大的是U2R攻击,仅降低了3.49%,PSOBP算法降低误报率幅度最大的是DOS攻击,仅降低了4.35%。 表4 4种攻击的仿真结果 为了使得实验结果公平,4种算法均采用与检测正确率及误报率对比试验相同的参数,即输入层节点个数为41,中间的隐藏层节点个数为30,输出层节点个数为5,学习率固定为0.1,实验误差设定为0.001,初始因子设定为0.95,最大迭代次数为500次,种群数均设为30,如表5所示。 图4(a)~图4(c)分别为GWOBP算法、PSOBP算法及改进BSOBP算法的收敛曲线。实验检测率和迭代次数如表6所示。 表5 参数设置 图4 3种算法的收敛曲线 表6 检测率和迭代次数 由图4和表6可知,传统BP神经网络的训练次数为1 000次,检测率为90.74%,GWO优化的BP神经网络的迭代次数超过了设置的最大迭代次数500次,适应度的数量级为10-1,相比传统的BP神经网络,检测率提高了0.82%,仅对传统的BP神经网络起到了一定的优化改进效果,而使用PSO算法优化的BP神经网络相比传统的BP神经网络,检测率仅提高了2.24%,但明显提高了BP神经网络的收敛速率,减少了迭代次数。由图4(b)和表6能够看到,用PSO算法优化的BP神经网络的迭代次数和检测率分别为200次和92.98%,可该算法的适应值的数量级仅是10-2,但改进的BSO算法优化的BP神经网络适应度却接近数量级10-3,且迭代次数和检测率分别为66次和97.87%,相比传统BP算法的及其他算法优化的BP神经网络无论在收敛速度及迭代次数上都有了极大的改进。 本文的改进天牛群算法使用Tent映射方式来产生初始的天牛群体、动态的感知因子及导向性的学习策略来改进传统的BP神经网络,使BP神经网络得到最优的初始权值和阈值,从而有效解决了传统BP神经网络算法初始值随机性较大、易陷入局部最优和收敛较慢等问题。由仿真实验结果可以看出,改进的天牛群算法优化的BP神经网络检测率和迭代次数分别为66次和97.87%,检测率和迭代次数方面都有了较大的改进。所以无论是从检测率、误报率,还是收敛速度上看,本文算法都要优于其他3种算法。 用改进天牛群算法优化BP神经网络的初始权值和阈值,利用该算法产生一组最优的初始权值和阈值并赋予BP神经网络进行二次训练,有效避免BP神经网络陷入局部最优,加快了算法收敛速度。这种集成方法充分利用了神经网络学习能力强的优势,同时也利用了改进天牛群算法全局寻优的特点。在入侵检测的仿真实验结果中充分表明了改进后的天牛群算法检测率、误报率和迭代次数都优于其他3种算法,且具有较高的检测率、较低的误报率及较高的收敛速率,均证明了该优化算法的良好检测性能,体现出较好的应用成效和理论研究价值。在今后的工作中会使用更多的入侵数据集进行实验评估,找出其在不同数据集中的应用优势,并进一步研究该方法在入侵检测分类中的应用。2 BAS及BSO
2.1 BAS基本原理
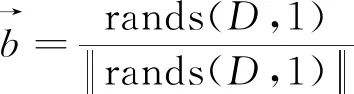
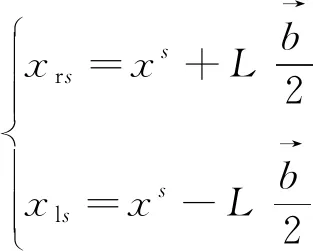
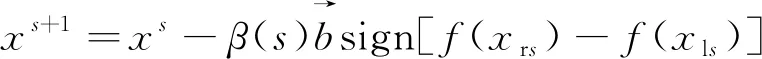
2.2 改进的天牛群算法
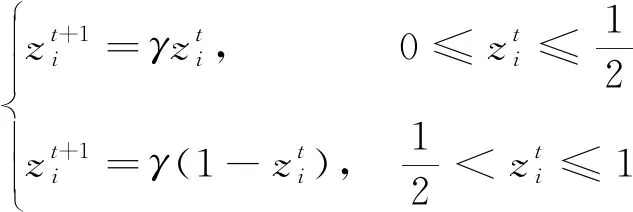
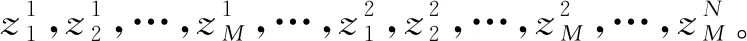
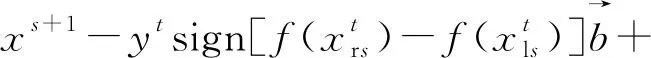

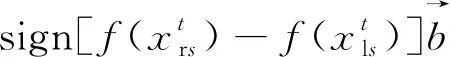
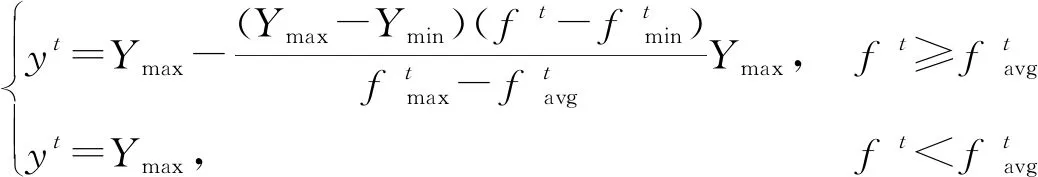
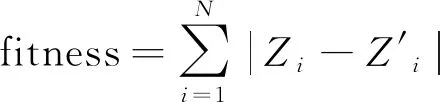
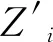
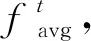
3 仿真实验与分析
3.1 数据预处理
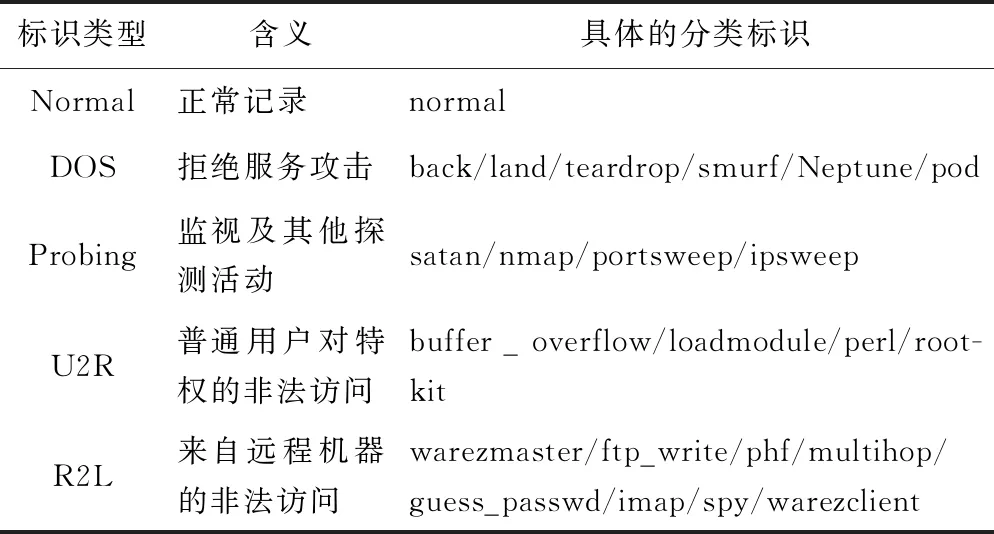
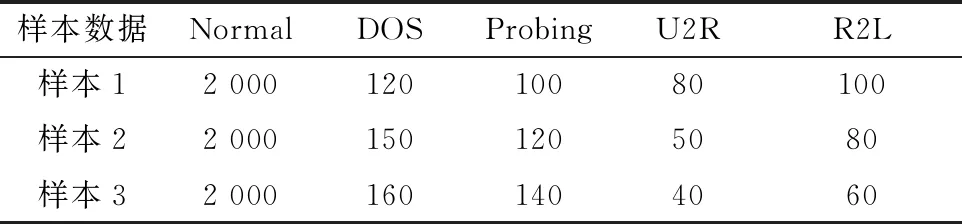
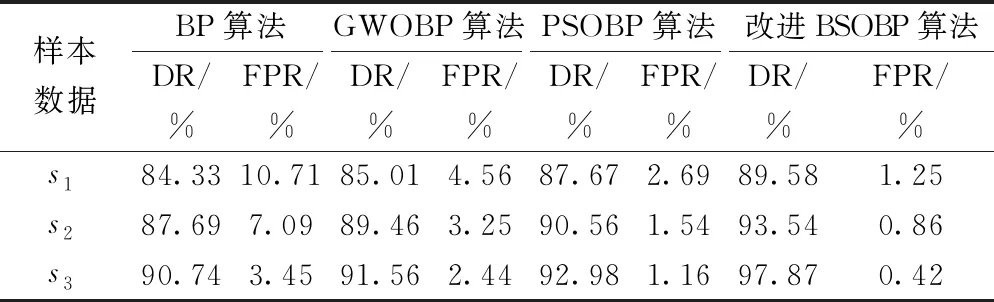
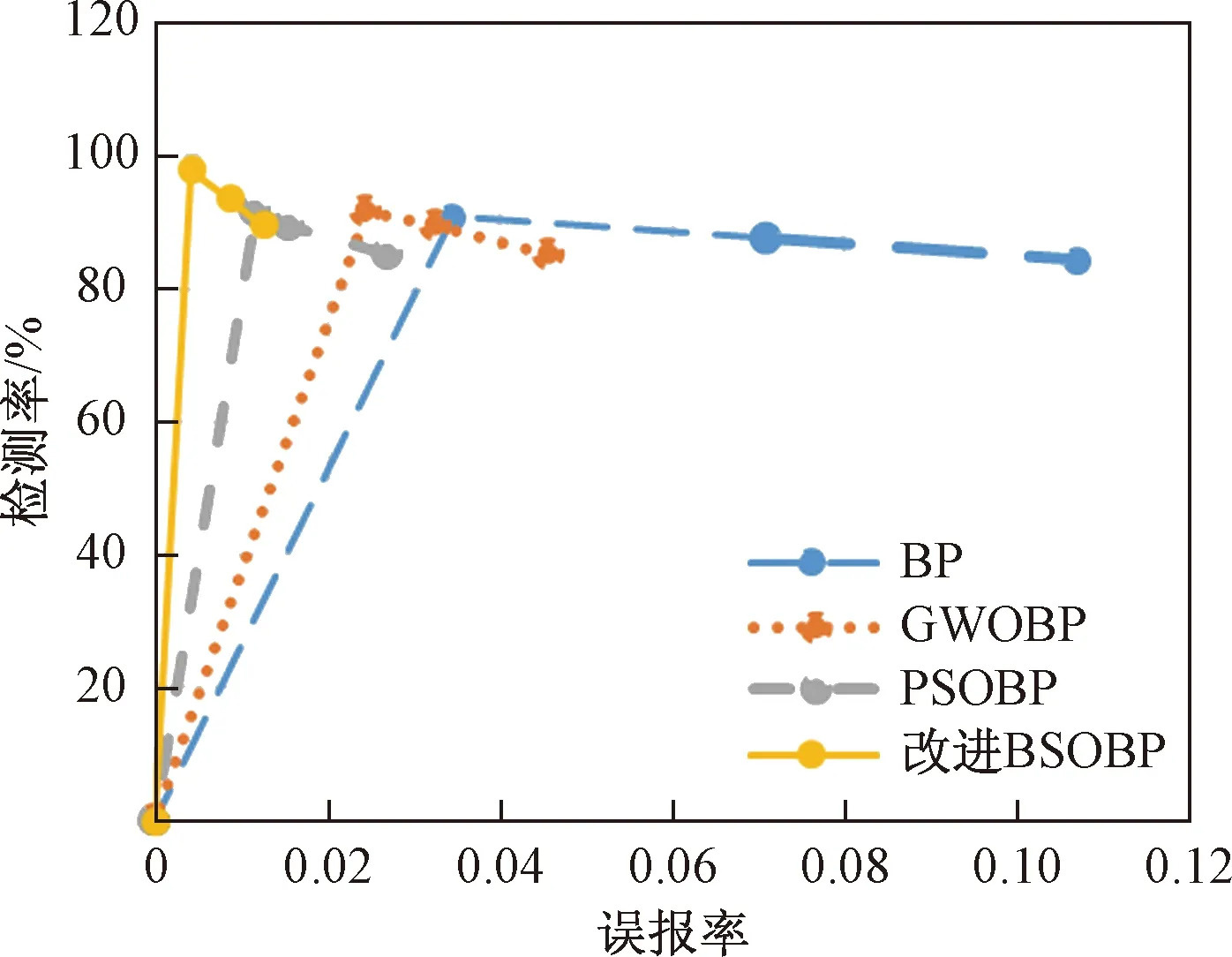
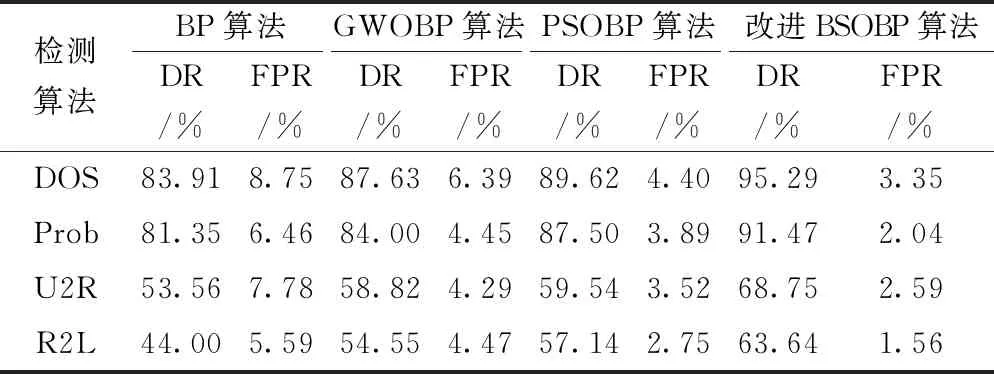
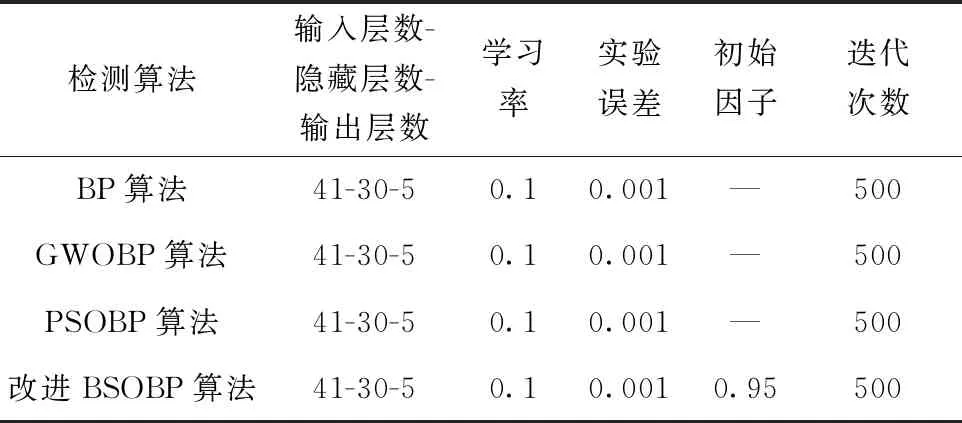
3.2 检测正确率及误报率对比试验
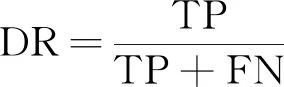
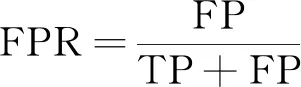
3.3 收敛速度对比试验

4 结论

