基于广义回归神经网络的风电机组性能预测模型及状态预警

崔 恺, 许宜菲, 李雪松, 杜亦航, 李 洋, 马良玉, 乔福宇, 刘卫亮

(1.新天绿色能源股份有限公司, 石家庄 050051； 2.华北电力大学自动化系, 保定 071003)

风力发电机组长期承受变动的载荷和复杂的气象条件、工作环境恶劣,随运行年限增加其性能会逐渐劣化,故障率提高。风力机监控与数据采集(supervisory control and data acquisition,SCADA)系统全方位记录了机组的历史运行参数,为风机性能评估和状态预警提供了可靠的大数据来源。利用SCADA数据实现风机运行性能评估、状态监测和故障预警,已成为近年来的研究热点[1-9]。

基于SCADA 数据的风电机组性能评估和状态预警研究大致可分为两类：一类是借助SCADA数据使用统计学方法直接判断机组是否存在潜在故障[3-5]。这种方法比较适合于具有较大随机性、不易建立明确模型的齿轮箱轴承温度、变桨驱动器温度等参数监测和预警。另一类是从SCADA系统中抽取机组正常运行数据建立预测模型,对当前工况应达值进行估计,并与实际运行参数对比来评判机组的运行状况[6-9]。这种方法尤其适合与风机运行机理和控制密切相关的发电机转速、功率等参数监视和预警。

人工神经网络(artificial neural network,ANN)由于具有很强的自学习能力,在复杂工业过程建模、预测和诊断领域广为应用。采用BP、Elman等常见神经网络进行建模时,网络结构不能自动寻优确定,模型收敛速度和精度与训练算法有关,有时易陷入局部最优。广义回归神经网络(general regression neural network,GRNN)作为一种建立在数理统计基础上的神经网络,将转移函数以概率密度函数替代,从观测样本里求得自变量和因变量之间的联合概率密度,直接计算因变量回归值,具有学习速度快、逼近能力强、调节参数少等优点,在系统辨识和预测控制等方面有不少应用实例[10-14]。

为此,结合风电机组运行和控制原理,分析影响其主轴转速和发电功率的主要因素,进而确定机组动态特性预测模型的输入输出参数[15]。利用某1.5 MW风电机组SCADA系统历史运行数据,对原始数据进行清洗和归一化处理,采用GRNN对风力发电机组特性进行建模。通过对比不同平滑参数取值下模型的预测性能,确立最优的风力机动态特性预测模型。在此基础上采用滑动窗口模型计算风电机组转速和功率的残差评价指标,实现风电机组运行状态预警。

1 广义回归神经网络原理

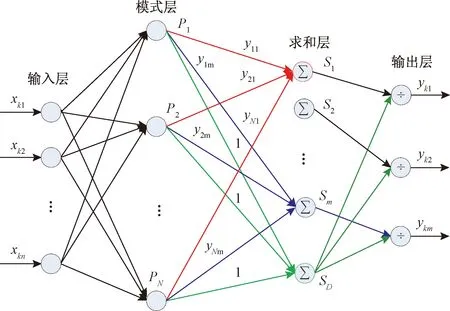
图1 GRNN神经网络结构

广义回归神经网络(GRNN)是由Specht提出的一种新型的非线性回归的前馈式神经网络模型,其结构包括输入层、模式层、求和层和输出层,如图 1 所示。图1中,输入层神经元的数目与输入向量X的维数n相同,输出层神经元的数目与样本输出向量Y的维数m相同。输入层神经元不进行运算,直接将输入变量X传递给模式层。模式层又称为隐回归层, 模式层的神经元数目和学习样本的总数目N相同。

现假设：

(1)

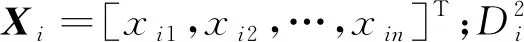
(2)

式(2)中：σ为平滑参数。

求和层共有2个单元组成,分别求取用于输出层计算的分子项和分母项。其中,第1个单元与输出向量维数m对应,共有j=1,2，…,m个节点。第j个节点输出Sj为网络训练集中第i=1,2，…,N个样本的输出向量Yi=[yi1,yi2,…,yim]T中的第j个元素yij与模式层第i个神经元输出Pi的加权和(即以yij当作模式层中第i个神经元Pi与求和层中第j个神经元间的连接权值),其计算式为

(3)

求和层第 2 单元只有1个节点,输出SD为模式层各节点输出Pi之和(作为输出层各节点计算的公共分母项),其计算式为

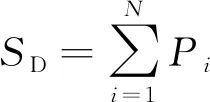
(4)

输出层的神经元个数与输出向量Y维数m相同,各神经元的输出为求和层中两种求和结果相除,即

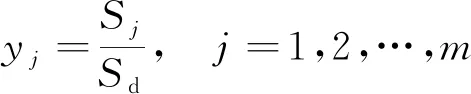
(5)

由上可见,对于GRNN算法,当所输入的训练样本集确定,神经网络训练本质上是确定平滑参数σ的过程,网络的预测性能与平滑参数σ的取值有很大关联,选择合适的平滑参数值是提高模型预测精度的关键,需结合模型训练样本和测试样本预测试验结果加以优选。

2 风机运行原理分析与模型参数选择

2.1 风电机组运行与控制原理分析

风力发电机组由风力机、主传动系统、发电机、控制系统等组成。其中风轮子系统是风电机组进行能量转换的重要部分,风轮捕获空气中的动能并将之转化为机械能,经主传动系统加速后传递到发电机,将机械能转变为电能。由于风速、风向具有极强的随机性,为确保风电机组运行在最佳状态,需要根据风机运行工况和风况对风机的叶片角度和机头工作状态进行调节。根据风速大小风电机组的运行状态可划分为4个阶段,即：启动区、最大风能捕获区域、恒功率区域及风速超限后的制动停机区[15],如图2所示。

图2 风速与功率的理想关系曲线

图2为风速与功率的理想关系曲线,而风电机组的实际运行包括诸多调节和过渡过程,机组转速、功率与风速的关系要更加复杂,需结合风电机组主控系统控制策略加以分析。

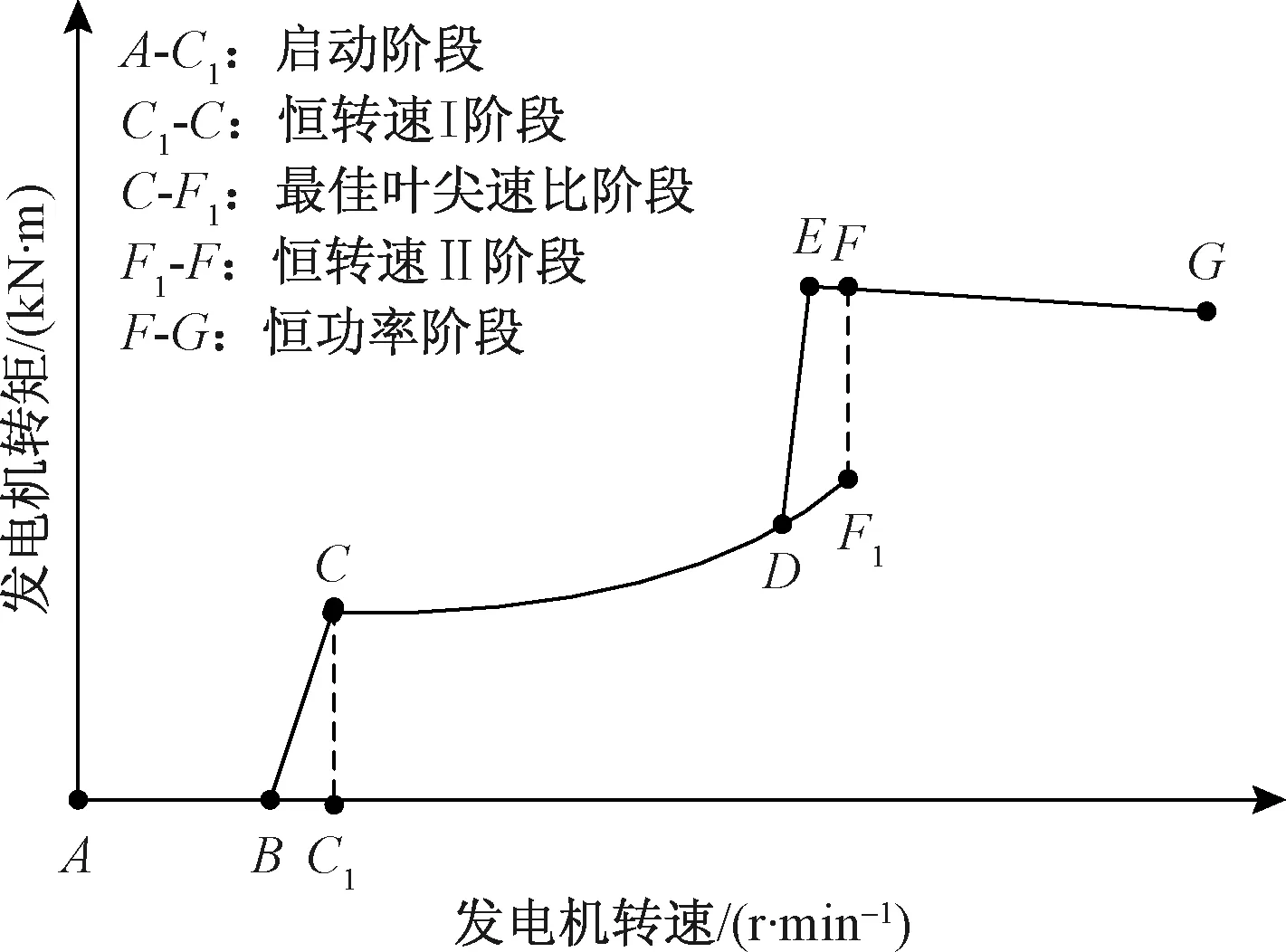
图3 风电机组运行区域示意图

大型风电机组主控制策略对应的机组运行区域如图3所示。其中发电机转速-转矩轨迹曲线为A-B-C-D-E-F。而实际的主控制策略曲线则调整为A-C1-C-F1-F-G以改善机组的性能,防止机组在额定点附近桨距控制器频繁动作,使机组运行更加平稳。在不同运行阶段,转矩控制器和变桨距控制器如何动作是主控制策略的核心。不同阶段转矩控制和变桨距控制的作用如表1所示。

由表1可见,除A-C1启动阶段外,各阶段转矩控制器始终根据当前转速输出相应的转矩设定值(转矩改变通过PI控制器调节变流器来实现)。而变桨距控制器则在不同阶段分别接受功率和额定功率设定值的偏差、转速及额定转速设定值的偏差,由两个PI控制器调节器输出桨距角设定值,驱动变桨距执行机构实现桨距调节[15]。

表1 不同阶段转矩控制和变桨距控制的作用

2.2 风电机组性能预测模型参数选取

风电机组SCADA 系统中记录了包括角度、速度、扭矩、功率、温度、压力、电流及振动等在内的近百个参数。旨在根据风电机组运行参数间的关系,确定各子系统运行控制性能是否存在异常,因此对轴承温度、振动等参数不予考虑。主轴转速作为风轮子系统的输出参数,偏航系统工作不正常、桨距角控制异常等均可由其异常变化反映出来。而主传动系统正常工作时齿轮箱有固定的增速比,其输入为主轴转速、输出为发电机组转速,二者间存在线性倍乘关系。因此可选择发电机组转速作为模型的输出参数。若考虑包括发电子系统在内的整机性能,应将功率也作为模型的输出参数。

由上文分析可知,风电机组运行中转速及功率除了与风速有关外,还受机组控制系统调节过程的影响。桨距角调节异常会影响主轴或发电机转速。同样的发电机组转速下,通过改变转矩设定值调节变流器改变发电机功率,而转矩的变化也会对发电机转速产生影响。此外,由于风向瞬时波动频繁,正常运行时偏航系统会自动对风以维持机舱中轴线与风向夹角小于规定的允许偏差。若偏航系统调节异常,同样风速下风机的转速和功率也会异常下降。

综上所述,与主轴转速(发电机转速)和功率相关的参数包括风速、风向、机舱中轴线与风向夹角、桨距角(设定值),发电机转矩(设定值)等,为此选择表2所示参数作为模型的输入和输出。

表2 性能预测模型输入/输出参数选择

3 风机机组特性预测模型的建立

3.1 SCADA数据预处理

以某1.5 MW风电机组为例,从SCADA系统选取三个月历史运行数据进行建模(采样周期1 min),原始数据共计123 420组。去掉其中的空值、风力机启动状态(风速≤3)和停动状态(功率≤零)的数据后保留正常运行数据88 582组,据此绘制风速-主轴转速、主轴转速-发电机转速、发电机转速与有功功率、风速-有功功率的统计曲线,如图4所示。

由图4(a)、图4(b)可见,由于风速、风向的随机快速变化以及风电机组的控制系统、偏航系统等存在控制误差,风电机组运行数据中的风速-转速、风速-功率数据关系呈带状分布,且 “F”型表明机组存在各种原因限负荷的工况。由图4(c)可见主轴转速与发电机转速近似呈线性关系。由图4(d)可见,同样的发电机转速对应的有功功率并不唯一,这与发电机转矩调节相关。上述分析说明表2建模参数选择的合理性。

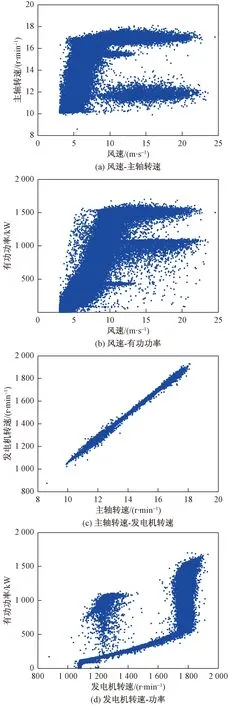
图4 风电机组运行中主要参数统计关系

本研究旨在建立风机正常运行工况性能的预测模型,据此对异常工况进行预警,为此需要对上述数据进一步过滤,以去掉其中不符合机组正常出力特性的异常运行点,如各风速下发电机转速、功率明显偏离标准值很多的散点及限负荷工况点(F型曲线的下横线)。为此采用文献[16]的滤波方法对数据进行清洗,最终得到用于模型训练的正常工况数据82 074组。数据清洗后的风速-发电机转速,风速-有功功率关系曲线如图5所示。

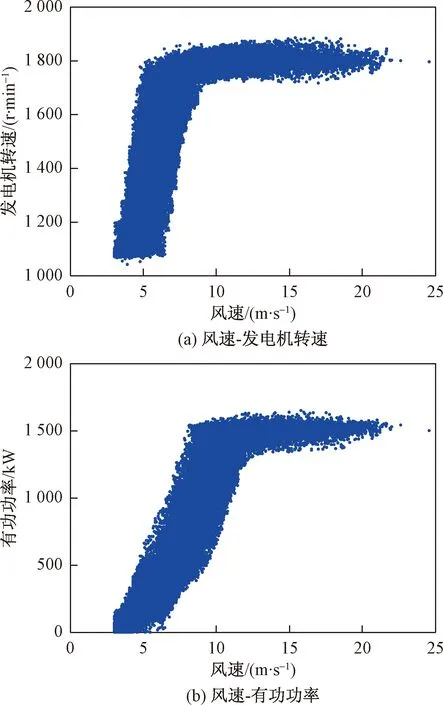
图5 数据清洗后风速与发电机组转速、功率间关系

由于不同运行参数量纲不同,为使各变量对模型的输出的作用均衡,需预先对训练样本进行归一化处理,将各个输入、输出参数的尺度控制在相同的[0,1]区间。归一化公式如下：

k=1,2,…,N;j=1,2,…,p

(6)

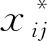
分别为原始训练数据集的最大值和最小值。

3.2 GRNN风力机性能预测模型的建立和验证

由于清洗后的数据量仍较大,选取前10 000组数据建立GRNN模型,并从后续数据中选取10 000组测试数据对模型进行验证。考虑光滑因子σ对网络的性能影响比较大,分别取不同光滑因子σ建立GRNN神经网络预测模型,比较不同σ取值时模型的训练精度和验证精度,结果如图6所示。

图6 不同σ取值对模型预测精度的影响

由图6看出,随着σ取值从0.01逐渐增加,模型训练集的平均偏差单调增加,而验证集的平均偏差则先下降后增加,且当σ取0.023/0.026时,验证集转速、功率平均偏差分别达到最小值17.27 r/min、19.31 kW,随后逐渐增加；考虑模型的预测性能最佳,最终选用σ取值为0.023的GRNN模型作为最佳模型,用于风机运行性能评估及故障预警。对应于训练集和测试集的模型转速及负荷预测值和实际值对比、绝对误差曲线如图7、图8所示。

图7 光滑因子σ=0.023时的模型训练结果

图8 光滑因子σ=0.023时的模型校验结果

4 基于滑动窗的风机状态预警方法

4.1 滑窗模型

风电机组性能预测模型建立之后,即可利用该模型对某一时刻发电机转速、功率进行实时预测,并与机组当前时刻的实际转速、功率进行对比,若偏差超过设定的阈值则发出预警。然而,由于风速具有较强的随机性且风机控制始终处于动态调整过程,而SCADA数据为分钟级数据,不能排除在单一时刻模型的预测误差可能会很大。若基于单一时刻模型预测值和实际值的偏差进行状态预警,出现错误报警的概率很高。为此,采用随时间推移的滑动窗口模型来处理模型预测结果,通过计算窗口时间段内模型预测值与实际值的偏差指标,实现参数的异常状态识别[9]。

设窗口宽度为h,窗口每次移动增量为q,则第k个窗口的数据集为时间tk-h至tk的SCADA数据(其中Xi为ti时刻的输入数据集),第k+1个窗口的数据集为时间tk-h+q至tk+q的SCADA数据。当tk-h至tk时刻数据处理完毕,窗口两端沿时间递增方向同时移动q,再处理tk-h+q至tk+时刻的数据矩阵。滑动窗口模型如图9所示。

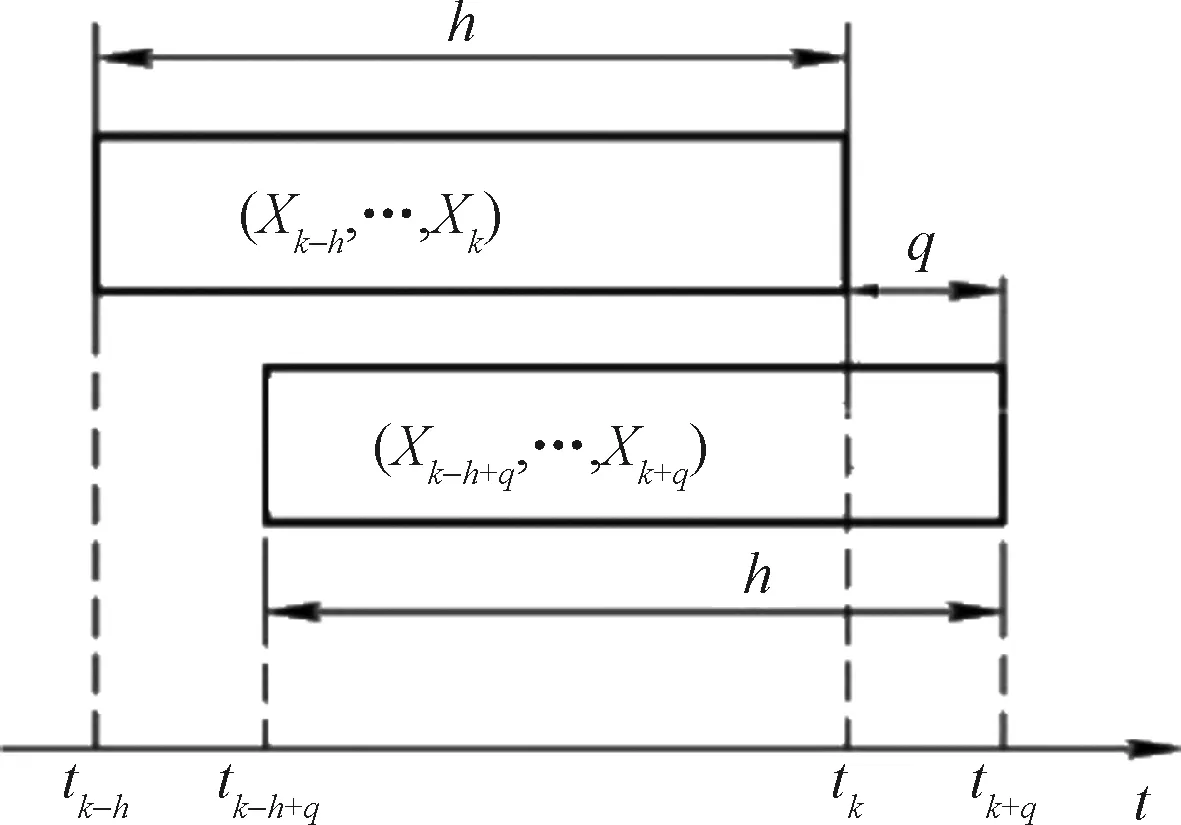
图9 滑动窗口模型

窗口宽度h对应的数据规模与预测指标的稳定性和滞后性有关,合理的数据长度须保证数据段内平均预测结果稳定,有效避开模型单点误差的影响,且不会使预测指标产生过大的迟延。而增量q对应计算更新频率,须保证计算机有足够的处理时间获得这些数据之间隐含的状态参数关系。预警过程的最优窗口宽度h和增量q需经试验合理确定。

图10 异常状态预警实例1

4.2 评价指标及阈值确定

基于上述滑动窗模型,对第k个窗口采用窗口时间段内各参数预测值与实际值的平均偏差(MAE)作为运行状态的识别指标,其具体表达式为

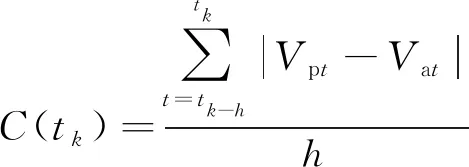
(7)

式(7)中:Vpt、Vat分别为t时刻的参数预测值和实际值。

评价指标C(tk)量化了风电机组相对正常运行状态的偏离程度,指标越小,参数越接近正常状态；指标越大,偏离程度越大。当指标超过预先设定的阈值时则可判定该参数出现异常。

阈值取值过大或过小会影响参数预警的误报率和漏报率,需借助试验合理选取。一种简单的方法是参考模型在校验样本集上的预测误差平均值和最大值,取平均预测误差的2～3倍作为报警阈值,具体倍数可根据试验适当调整。 另一种方法是利用本文建立的GRNN模型,采用滑动窗方法选取一段时间的正常运行数据,求取一系列评价指标,并基于小概率事件假设,计算置信上限Cth作为阈值[9]。采用第二种方法,阈值具体计算式为

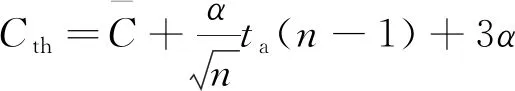
(8)

5 故障预警实例

为验证预警方法的有效性,基于MATLAB编制了具有图形用户界面的故障预警软件,选取建模机组2018年的真实历史运行数据进行测试。报警阈值设置按照上文所述,调用已经训练好的GRNN神经网络模型和校验样本集,当取α=0.000 5时,利用式(8)计算可以得到状态指标异常阈值Cth1=52.77,Cth2=43.73。

5.1 故障预警实例一

将该机组2018年历史数据导入MATLAB,筛选掉风速小于切入风速的数据,取第8 221条即2018年1月19日00:44作为数据的起始点,运行状态预警软件,系统自03∶21、08∶20分别连续出现“转速及功率偏差大”异常报警,软件记录了机组报警信息及出现报警的时刻,如图10所示。

查看机组真实历史故障列表,发现在 2018年1月19日03∶41、09∶26多次出现了“主控没有收到变桨EFC反馈信号重复出现”故障,分别历时4.16、3.16 h,导致机组状态异常自动停机。软件预警系统对上述故障及时正确地给出了预警,验证了本文模型和预警策略的正确性。

5.2 异常状态预警实例2

对同一机组,状态监测系统2018年9月13日自21:30起连续发生“转速及功率偏差大”异常报警。查看机组历史运行数据, 21:44机组扭缆角度达867°,机组执行限负荷停机解缆操作,历时约20 min约22:08解缆完成,扭缆角度变为136°,机组重新恢复运行。同样,状态检测预警系统对上述异常状态及时正确地给出预警,如图11所示。

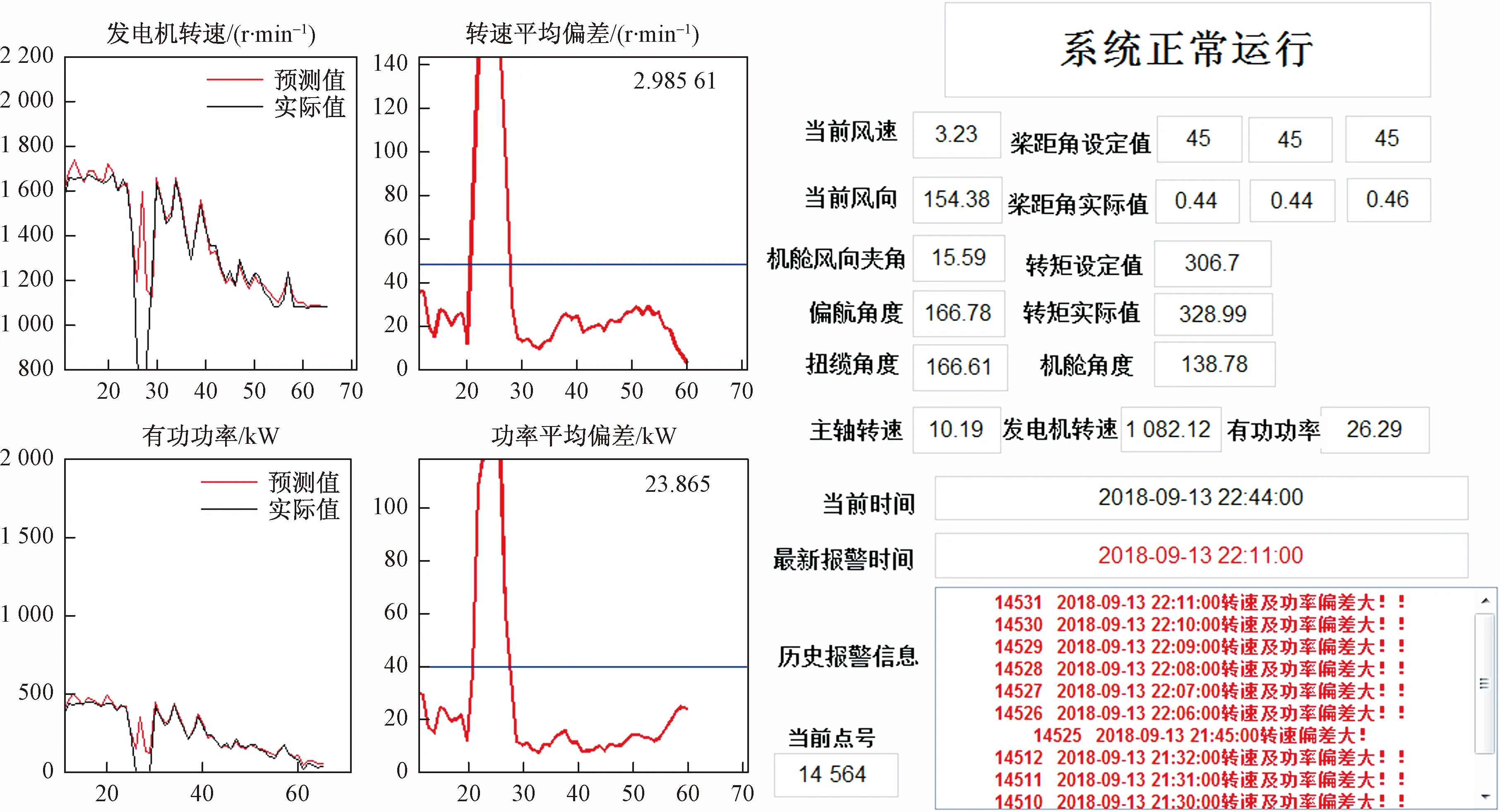
图11 异常状态预警实例2

6 结论

通过分析风电机组的运行和控制机理,以某风电场1.5 MW风力机为对象,建立了以发电机转速、有功功率为输出的GRNN神经网络预测模型,通过比较不同光滑因子取值σ对模型预测性能的影响,确立了最优的风机机组性能预测模型。

以此模型为基础,提出一种基于GRNN和滑动窗口模型的风电机组运行状态评估及预警方法,该方法完全基于正常运行状态的数据进行分析,无需任何异常状态的先验知识。以上述方法开发风机状态检测及预警软件,采用风机的真实历史故障案例进行验证,表明本文方法可以及时正确地检测风电机组的异常状态,对风电机组运行状态预警和维护决策具有重要意义。