浅析量子排斥力

袁贺滔

（广东东莞市石龙中学，广东 东莞523320）

1 牛顿万有引力定律遗留的问题。

牛顿提出的万有引力定律的公式是

公式不是由更深层次的规律推导出来，因此，公式的提出实质是假设性质的，是否正确，由日后的实践检验。

公式中m 代表的是质点，即，质量为m 的几何点。牛顿提出万有引力定律时没有指出，或说没有考虑定律在空间的适用范围，也即公式中的两质点之间的距离R，从无穷远至0 都可用，这就留下如下的问题。

两质点在引力吸引下靠近，随着R 的缩小，F 增大，加速靠近。R→0，F→∞，最终两个质点重合成为一个新质点，质量等于（m1+m2）的几何点。新质点又可以和另一质点m3吸引，同样的过程重合为（m1+m2+m3）的新质点。如此类推的结果，这一几何点有无穷多的质点，质点之间的引力无穷大，质量密度无穷大，这就是“奇点”。

奇点、无穷大的值是物质的点模型和牛顿万有引力定律必然的数学结果，而这种数学结果却不可能是物理实在，这种矛盾又称为“无穷大困难”。

2 如何克服无穷大困难？

2.1 物质的质点模型是不可能放弃的，从经典力学到量子力学，从牛顿三大定律到薛定格方程、电子狄拉克方程，表述的对象都是质点，人们至今找不到一个可以代替质点的模型。

2.2 如果给（1）设定一个限制条件，定律不能计算到某一个狭小的空间内，当然可以避免无穷大，但这种人为的限制实质是逃避困难，这个狭小的空间里始终都存在物理实在。

2.3 在铅用点模型的前提下，显而易见的克服无穷大困难的办法就是不让两质点重合，也即不让（1）中的R=0，当然不是指人为的设定，而是大自然的安排。刚好微观世界量子力学中的不确定原理，就是不让两质点重合在一起的天然的制约规律。

3 不确定原理

不确定原理的数学表达式是质点位置不确定量△x 和动量不确定量△p 的关系式

上关系式表明，当△x 减小时，△p 就增大，极端的情况，当△x=0，则△p=∞，虽然无穷大的△p 是一个不确定量，但表明质点存在取极大动量值的概率。不确定量关系式的其中之一的物理意义，可以理解为：

如果有一种机制，压缩或说禁锢一个质点的活动范围，即△x 减小，不确定关系规律就会加大动量不确定量，对抗这种机制对质点活动范围的压缩，这种效应相当于有一种排斥力对抗压缩力。极端的情况，这一机制把质点禁锢在一个点，不确定量关系就会由于△p=∞，令质点具有极大动量的概率，使得质点被禁锢于一点的事件不可能发生。

吸引力令两质点的距离R 缩短，相当于是一种压缩质点活动范围的机制，如无其他机制的干扰，会发展到极端情况，两质点会重合。但正正是不确定原理令质点产生一种排斥效应，对抗吸引力压缩质点的活动范围，令重合的事件不能发生。

因此说，不确定原理是解决“无穷大困难”的天然规律，比人为的“重整化”方法更合理，不确定原理赋予质点一种对抗压缩它的活动空间的排斥力。不确定原理与物质点的物理性质，比如与质量、电荷等无关，只要是微观客体（粒子），或说物质点，不管物质点的物理性质是什么，管制微观世界的量子力学就会赋予物质点这种排斥力，因此是一种万有的力，阻止两物质点无限接近。

参考“万有引力”的命名，这种排斥力可以称为“万有排斥力”，用符号Fq表示。这种排斥力来源于量子力学规律，又可命名为万有的“量子排斥力”，或简称“量子排斥力”是量子力学所特有的。

4 不同类型的（1）式和（2）式如何融合

大自然存在得很巧妙，万有引力管治宏观世界，万有斥力管治微观世界，特别是深层次的微观空间。但大自然的世界应该是一个完整的世界，那么两种类型完全不同的数学式（1）和数学式（2）又如何融合呢？薛定格方程正是一个很好的示范，薛定格方程是量子力学的波动力学方程，但方程里却有一个原封不动的经典力学的库伦力场，因此，不同类型的（1）式和（2）式融合的方法如下：

我们可以设计一个既反映不确定原理效应，又属于经典力学类型的量子排斥力，以便能够像库仑吸引力那样，一起放入量子波动力学方程中。

5 万有的量子排斥力Fq

万有引力公式（1）是一个假设性质的公式，为避免过多的思考过程的书述，本文在此直截了当地提出假设性质的量子排斥力Fq公式

其中D1和D2分别是两个微观物质点的“力荷”。由于不确定关系式与物质点的物理性质，比如与质量、电荷等无关，只跟微观世界的普适常数普朗克常数h 有关，因此设定

式中c 是真空中光速，如此（3）可写成

万有的量子排斥力公式

可以验证Fq的量纲是牛顿。这公式不是由公式（2）推导出来的，因此与万有引力公式一样是假设性质的，是以另一种形式反映不确定原理的效应。待定常数r0的单位是长度，或称为“特征尺寸”，它反映排斥作用开始显现的微观空间尺寸。r0是一个很小的数值，以保证Fq是一种深层次的微观空间才起作用的力。如第4 节所说的，

（1）式和（2）式融合的办法是把引力和斥力（5）加在一起，把合力放入波动力学方程中。

并且，引力不单是万有引力，还包括库伦引力，甚至恒星坍塌时的向内的压缩力。作为典型的例子，一个质子和一个电子相互作用，合力可写为

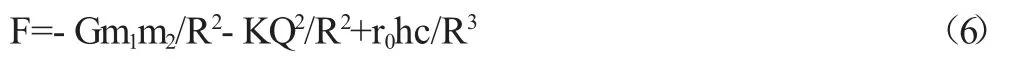
上式以排斥力的方向为正，吸引力的方向为负。微观粒子的质量很小，作为两个微观粒子的相互作用，当有库伦吸引力出现时，万有引力一项就可以忽略，于是在实际上，（7）式可以写成

作为一种估算，这里暂时设定

在此设定下，作为一种感性的认识，以下是在关键点位库仑力Fe 与万有排斥力Fq 的对比

当R=10-8米，Fe=2.3×10-12N Fq=2×10-17N

当R=10-14米，Fe=2.3N Fq=2×10N

当R=10-16米，Fe=2.3×104N Fq=2×107N

当R=10-20米，Fe=2.3×1012N Fq=2×1019N

（1）R=10-8米是氢原子基态的尺寸，是从宏观世界开始进入微观世界的空间，可以看出，Fq 只是Fe 十万分之一，量子排斥力的引入对氢原子的原有的量子力学的讨论没有影响。

（2）R=10-14米是接近特征尺寸r0的点位，可以看出量子排斥力开始大于库伦吸引力。

（3）R=10-16米是开始进入深层次的微观空间的点位，量子排斥力已是库伦吸引力的一千倍。

（4）R=10-20米是已进入到深层次的微观空间的点位，此时，量子排斥力已经主导这种空间。

可以预计，电子向质子进发的过程必有一个平衡位置R0，排斥力与吸引力刚好对消，此数值可令（7）中的F=0 求得，此时

由量子力学氢原子理论知（

其中a 是精细结构常数

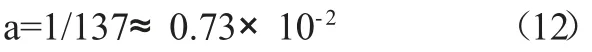
于是

6 经典谐振和量子谐振

作为感性的认知，在平衡位置附近，电子在库伦吸引力和量子排斥力共同作用下会出现经典谐振。现在给以数学表述。

其中R0由（9）和（13）表示，即R0=r0/a 并有

合力方程（7）可以写成

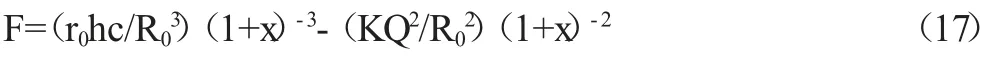
我们只讨论x＜＜1，即x 比1 小很多的情况，以致数学上的泰勒级数展开式中，可以只取头两项，即（1+x）-2=（1-2x）和

如此（17）式变成

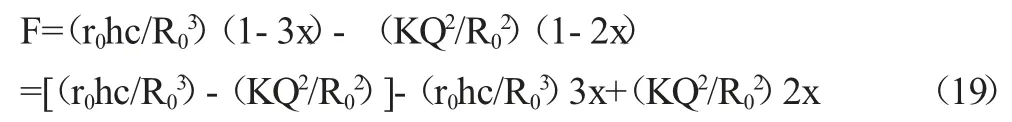
因有（16）式，则由上式得

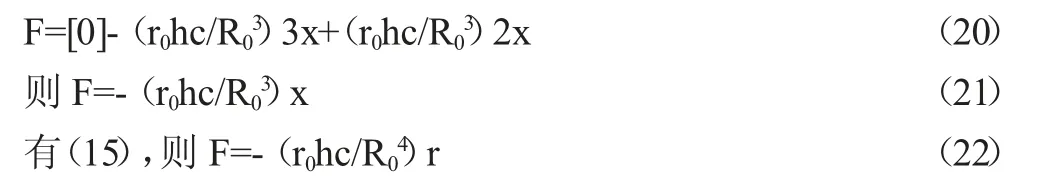
上式正是经典力学弹性力的数学形式，可以写成

k 就是弹性系数。如果把（13）式代入，则，弹性系数又可以写成

可以验证k 的量纲，k=（焦耳秒）（米/秒）/米3=牛顿米米/米3=牛顿/米，正是弹性系数的量纲。

在弹性力（22）的作用下，电子就成为一个经典的谐振子，其平衡位置是R0，按已有的经典力学规律，就可写出，振子的角频率ω2=k/me，把k（24）代入得

按已有的经典力学规律，写出弹性势能

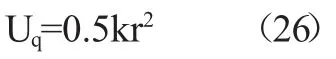
以上的讨论过程基本上是经典力学的过程，但在R0附近的空间是微观空间，服从量子力学规律，因此，这个经典谐振子实际是量子谐振子。在数学表述上，正如第4 节所说，可以简单地利用氢原子电子的薛定格方程，把方程中的经典库伦场势能U=-KQ2/R 用（26）的经典弹性势能代替，就得量子谐振子的定态薛定格方程

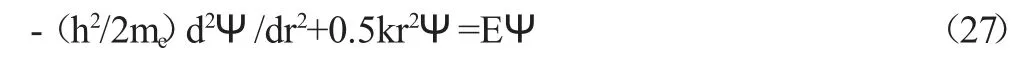
上述方程的解有系列能量本征值

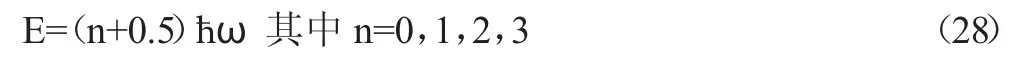
最稳定的状态是n=0，即零点能ε

角频率ω 见（25）式。

由此可见，包括宏观世界和微观世界的宇宙，来回往返的振动才是最基本的运动形式。

7 尝试用中子模型确定r0 的数值

恒星坍缩造成的巨大压缩力，足可以令原子的基态崩溃，在库仑吸引力作用下质子和电子结合在一起，成为中子。但在量子排斥力的对抗下，在平衡位置R0附近形成量子谐振。为尝试在引入量子排斥力的概念下，对中子进行计算，在此提出一个中子模型：

中子是质子和电子组成的量子谐振子。

实验已测得三者的质量是，

质子mp=1.6726231×10-27千克

电子me=9.1066×10-31千克

中子mn=1.6749286×10-27千克

那么，mp+me=1.6735338×10-27千克

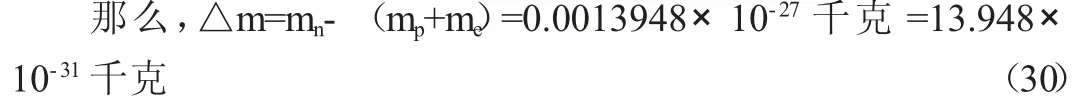
可见，中子的质量比质子和电子的质量之和还大，那么，质量差△m 所相应的狭义相对论的能量△mc2就相当于量子谐振子的（13）式的零点能量ε=0.5hω（n=0 最稳定），即

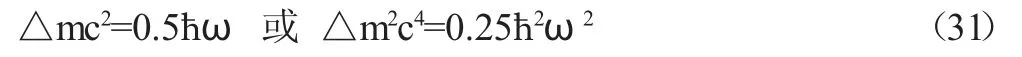
把ω2（25）代入上式的第二式得

经移项整理后得

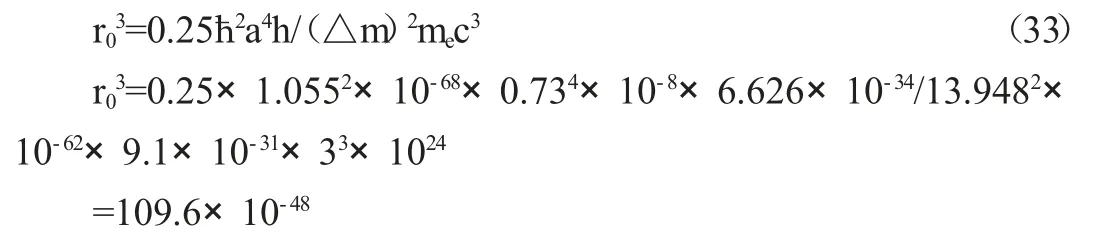
最后得

8 振动是最基本的运动形式

任何粒子只要有内部结构，至少由两部分物质组成，这部分物质直称为“结构物质”，既然在理论研究时，把粒子作点模型质点处理，那么，“结构物质”也只能作“结构质点”处理，也就是说一个粒子（至少）由两个结构质点组成。如果这两个结构质点之间没有某种吸引力维系，不可能构成一个粒子，但如果除了吸引力之外没有其他因素干扰或说制约，这两个结构质点又成为一个点。点模型只能是一种数学模型，不可能是真实的物理存在。正好本文引入的万有的量子排斥力成为一种干扰制约的因素，两结构质点在吸引力和量子排斥力的共同作用下组成量子谐振子，而不是在吸引力作用下结合成一个点。

9 结论

因此，各种各样的粒子其实是各种各样的量子谐振子，也可以说，对于包括宏观世界和微观世界的宇宙，来回往返的周期性振动是最基本的运动形式。