耦合H-minima与数学形态学的分水岭遥感图像分割方法

何安良， 程兴保， 廖龙长， 程朋根

(1.湖南中核建设工程公司，湖南 长沙 410119；2.南昌昌鸿勘测设计咨询有限公司，江西 南昌 330038；3.东华理工大学 测绘工程学院，江西 南昌 330013)

遥感图像分割是从遥感影像中提取感兴趣的区域，以减少后期图像分析和理解的数据量，同时又保留了图像的结构特征信息，能使原始图像成为更加抽象和简洁的形式(陈秋晓等，2006；高丽等，2007；李欣腾等，2017；王升等，2019)。

大体上，遥感图像分割方法可分为四类：基于阈值的、基于区域的、基于边缘的和基于特定理论的分割方法(Bieniek et al.，2000；肖鹏峰等，2007；Trias-Sanz et al.，2008；刘建华等，2009；Tarabalka et al.，2010)。图像分割算法众多，其中基于分水岭分割的方法是最为常用的算法之一(马丽红等，2003；王勋等，2007)。该算法可快速分割图像成一系列具有闭合曲线包络的图斑，被广泛应用于遥感图像分割。蔡利平等(2015)利用边缘走向对遥感图像进行自适应多尺度分割获得比传统分水岭算法更优的结果；陈会斌等(2017)利用Sobel梯度算子重建高分遥感图像的边缘图像并二值标记，然后通过分水岭方法对其进行分割；闫鹏飞等(2018)针对高分辨率遥感图像引入尺度自适应分割方法以达到分割参数自动选取的目的；冯朝晖等(2019)利用分水岭算法对叠加前景图与背景图组合而成的标记图进行遥感图像分割；李攀峰等(2019)通过加权混合梯度来实现对多光谱遥感图像分水岭分割。这些方法虽然在一定程度上缓解了传统分水岭方法过分割现象，但对遥感图像中的噪声与局部纹理依然敏感，边缘定位精度有待提高，且计算量较大。

为削弱噪声、局部纹理等干扰和避免分水岭过分割现象，笔者提出一种改进的分水岭遥感图像分割方法。该方法引入自适应滤波和数学形态学标记方法，构造一个自适应滤波器来削弱噪声、局部纹理等干扰，再进行分水岭变换得到分割图像。

1 改进的分水岭图像分割方法

针对传统分水岭遥感图像分割算法存在过分割问题，笔者提出了一种改进的分水岭遥感图像分割方法。首先，采用自适应滤波器对原始图像进行滤波以削弱噪声、局部纹理等干扰；其次，利用数学形态梯度算子计算滤波后图像的梯度；第三，对梯度图像进行数学形态重构并标记梯度图像；最后，利用分水岭算法分割图像(图1)。

1.1 自适应滤波算法

传统的分水岭分割算法易出现过分割现象，为减少噪声、局部纹理信息对图像分割产生的干扰，引入一种自适应滤波函数模型，以改善分水岭算法过度分割问题。该滤波模型如下：

(1)

1.2 数学形态梯度计算

采用数学形态梯度来增强图像并抑制平滑区域，为顾及各向同性，可选取半径较小的圆盘形结构元素以消除边缘方向对梯度计算的影响并避免产生厚边缘。数学形态梯度算子Grad为(王小鹏，2008)：

Grad(f)=(f⊕g)-(fΘg)

(2)

式中，f表示滤波后的图像，g表示结构元素，值得注意的是Grad(f)对噪声较为敏感但并不强化噪声，且该梯度算子运算得到的图像边缘厚度最少囊括了两个像素。

1.3 数学形态重构

上述形态梯度计算后存在噪声和局部纹理及量化过程产生的误差易导致局部“谷底”现象，且分水岭算法对于图像灰度的局部变化较为敏感，从而导致分水岭变换后易出现过分割问题。采用数学形态学开闭重构来去除因噪声、局部纹理产生的干扰并恢复地物轮廓。数学形态学开闭重构包括膨胀与腐蚀运算，假设梯度图像为g(x,y)、参考图像为r(x,y)以及结构元素b，则膨胀运算可表示为：

(3)

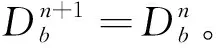
(4)

基于数学形态学开和闭重建的互对偶运算，其表达式为：

(5)

(6)

式中，∨表示逐点求最大值。梯度图像的数学形态学闭重建可表示为：

(7)

采用的数学形态开闭重建方法，能去除因部分噪声和局部纹理所产生的梯度图像局部极小值，从而减少因局部极小值对分水岭图像分割产生的干扰。

1.4 分水岭变换标记

在分水岭图像分割算法中，因图像灰度突变会产生局部极小值，传统的分水岭算法对于物体表面局部的灰度变化较为敏感，从而产生图像过分割问题。

为了改善这一现象，可对正确区域的局部极小值进行标记，并剔除错误的局部极小值，采用数学形态学标记扩展极小值变换运算H-minima对梯度重构的图像进行标记。H-minima是通过一个深度阈值h来过滤集水盆深度小于h的局部极小值，对集水盆深度满足上述条件的局部极小值进行强制标记，这一过程可表示为：

(8)

2 结果与分析

为了验证本方法对遥感图像分割的效果，选取了江苏省南京市江宁区城区和郊区的Landsat全色影像进行实验，两幅影像大小均为256×256像素(图2a，图3a)，包含256个灰度级，实验区包括建筑物、道路、水体和农田等地物要素。

本研究改进的滤波方法可消除部分图像中混杂的噪声且保留平滑物体内部的细密局部纹理(图2b)，但在边缘处仍然存在一些伪极小值区域，结合数学形态学的开闭重建可有效地减少此类伪极小值区域和突出目标地物，使图像边缘轮廓更为清晰，开闭重建后的图像见图2c。采用开闭重建后进行H-minima变换，对大于深度阈值的极小值区域进行标记，进一步减少极小值区域(图2d)，H-minima变换后去除了一些小集水盆区域和标记了集水盆深度大于深度阈值的极小值区域，以进一步减少过分割区域。通过对比，可看出本方法能有效解决分水岭方法过分割问题(图2e,f)。此外，采用本方法对郊区影像进行分水岭分割(图3)，同样可得到理想的分割效果。

与传统分水岭算法对比，本研究改进的算法从视觉上可显著减少过分割现象。图像中建筑物、道路和农田等地物大部分可被正确分割，分割效果相对较好。本方法包括3个主要的参数，即形态梯度计算的结构元素r1、形态开闭重构的结构元素r2和H-minima变换的深度阈值h。经多次试验发现，当r1=2、r2=1、h=31时，实验的城区图像分割效果最佳；当r1=2、r2=1、h=19时，实验的郊区影像分割效果最佳。

为进一步验证本方法分割效果，选取Otsu、Sobel、LOG等三种经典分割方法进行比较(图3d，e，f)，由于Otsu法只考虑像素点的灰度值而忽略像素点的空间分布特性，导致对灰度变化的过渡区分割效果不理想，所获取的目标轮廓宽度包含多个像素、降低了边缘定位的精度，且对于图像中一些过渡区域，比如绿地和道路之间的过渡区不明显，难以有效区分地物。采用Sobel和LOG的边缘检测算子对遥感图像中微弱边缘的响应不敏感，导致孤立的边缘像素点和一些建筑物的边缘出现了分割缺失，相对于Sobel算子而言，LOG的检测效果较好，但仍然存在分割缺失等问题。 本研究方法可有效减少分水岭的过分割区域，得到连续和封闭的边缘轮廓，可减少后期对边缘链接和跟踪等进一步处理。此外，表1给出了经典分割算法、传统分水岭以及本研究改进的分水岭算法之间的性能比较，对比了经典算法、传统分水岭算法、本研究分水岭分割方法在分割区域数量以及各分割算法的效率，可看出改进后分水岭的分割区域数量远少于传统的分水岭算法，大大抑制了过分割现象的产生。与Otsu和LOG算法相比，本研究方法在时效性上稍有不足，但综合分割的质量与精度，显著提升了传统分水岭遥感图像分割性能。

表1 城区与郊区影像采用不同方法分割的结果比较

3 结论

传统分水岭算法对遥感图像的细致局部纹理和噪声较为敏感，易产生过分割现象。针对这个问题，构建一个自适应的滤波器来减弱分割前局部纹理、噪声的影响，并对梯度图像进行数学形态学标记以减少过分割现象。采用遥感图像进行实验并与传统分水岭分割算法和经典图像边缘检测算法比较，改进的分水岭方法可明显减少过度分割区域和大幅提升传统分水岭算法在遥感图像分割方面的性能。