高考中有关椭圆曲直联立计算的思考
◇ 山东 王晨晨
(作者单位:山东省济宁孔子国际学校)
高考数学中有一道必考解答题,即圆锥曲线问题,并且此类大题一直处于压轴地位.解一题会耗时15~20 min之久,这很容易让学生失分.其实从曲直联立的一般情况推导,可以总结出一些规律,这将有助于此类问题的突破.在设而不求的曲直联立中,直线的设法无疑决定着计算的复杂程度,相信教师们都有总结,此文不再赘述.本文只介绍椭圆在高考环境下曲直联立计算中的一些规律,希望对广大师生有所帮助.
(a2A2+b2B2)x2+2a2ACx+a2C2-a2b2B2=0.
设x1,x2为其两根,记α=a2A2+b2B2,β=2a2AC,γ=a2C2-a2b2B2,则
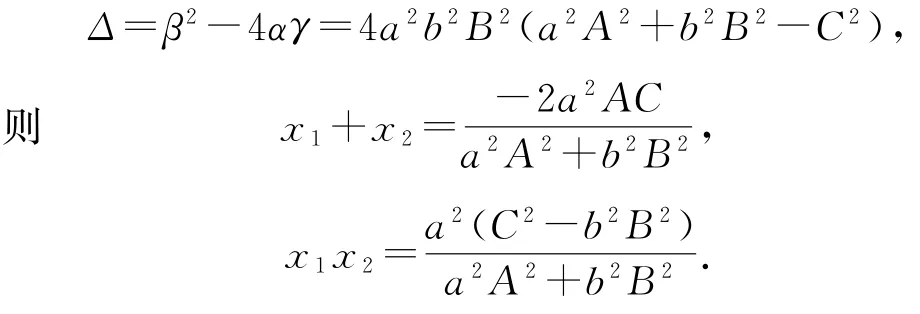
由对称性,我们将x 与y,A 与B,a 与b 均互换即可得消x 留y 的情形,即
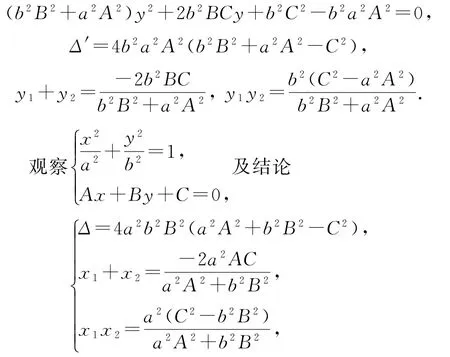
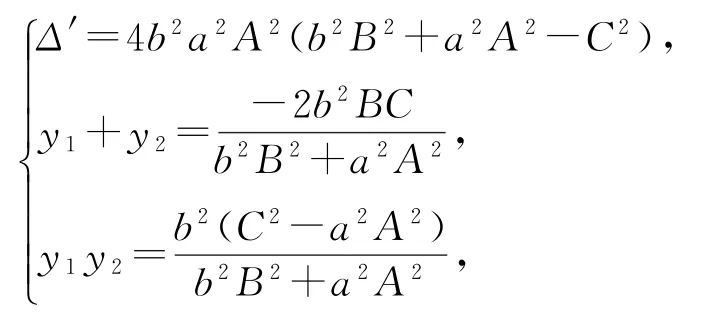
可以总结出如下规律.
① 两根之和与两根之积中有共同的分母α.
② 和式分子都为“-2倍”.
如计算x1+x2时,只关注式的等号左边,忽略含y 的项,只关注三项中所含字母a2,A,C,将其与“-2”相乘,即分子为-2a2AC.
③ 积式分子亦可大致记为分母α 中所表示未知数有关部分字母与(C2-另一部分)之积.如计算x1x2时,将分母a2A2+b2B2看成两部分,与x 有关部分a2A2,与y 有关部分b2B2,而分子为a2(C2-b2B2).
④Δ 与Δ′相近,但事实上我们构造直线方程时,若为y=kx+b,y-y0=k(x-x0),化为一般式后B=-1,Δ′=4a2b2(a2A2+b2B2-C2);若为x=ty+m,化为一般式后 A =1,Δ =4b2a2(b2B2+a2A2-C2).所以,计算时,有Δ=4a2b2(α-C2).
特别地,弦长公式
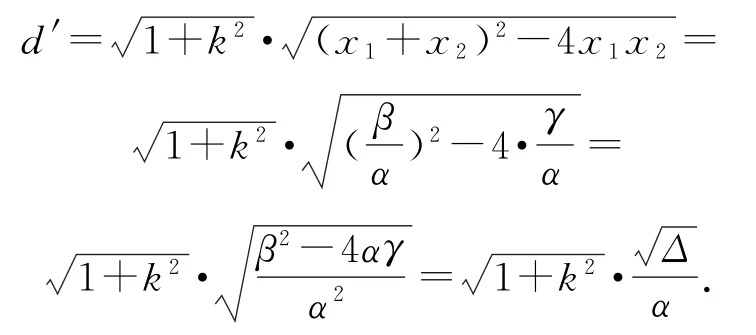
同理,另一形式
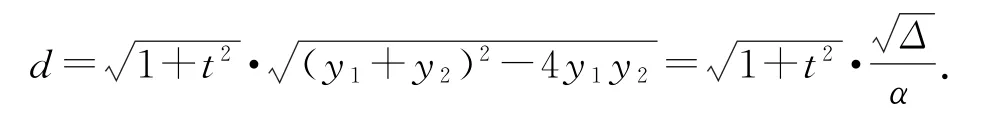
分析至此,相关计算结论的记忆与运用显然是可行的.而椭圆虽因焦点位置不同而有不同情形,但从形式上来讲两者无异,则椭圆中结论通用.
结论运用在计算中不只是能快速、准确地求出两根之和、积、判别式、弦长等常用数据,其更大的优势是代入后保留了同分母形式,无疑简化了形式,可提高后续计算准确率.教学时不宜急于推广结论,一定要等到学生经过一定量的曲直联立的充分练习后再进行.教学中教师首先应培养的是学生们的核心素养,切勿本末倒置,建议可放于一轮复习中.

