基于人工表面等离激元结构的超表面磁镜*

殷允桥 吴宏伟

(安徽理工大学力学与光电物理学院, 淮南 232001)

提出了一种表面粗糙磁镜的概念, 该界面由人工表面等离激元结构阵列设计而成. 这种人工表面等离激元结构通过周期性地将螺旋金属条插入到介电圆盘构造中以支持强磁偶极共振模式. 特别地, 对于不同外半径下的螺旋结构, 可以通过调节每个结构的螺旋度以支持相同共振频率的磁偶极模式. 为此, 设计了由多种不同尺寸的人工表面等离激元结构排列构成的粗糙磁镜, 计算了其效率并与光滑磁镜做了比较. 本文所提出的粗糙磁镜可以用来增强光与复杂结构的物质之间的相互作用, 亦可能应用于微波和太赫兹波段的生物传感和成像.

1 引 言

镜子在日常生活中随处可见, 并且在现代光学系统中起着重要作用. 传统的镜子主要是由贵重金属所制成的, 如完美电导体一样, 由于入射场与反射场之间的电场异相和磁场同相而在其表面产生零电场强度和最大磁场强度. 因为局部电场的大小可以决定光与物质相互作用的强度, 所以在传统的镜面附近会抑制这种相互作用. 由于电磁对偶性质, 具有完美磁导体边界条件的磁镜可以增强其表面的电场强度, 而不是磁场强度. 这种表面强电场分布对于磁镜界面处的光与物质的相互作用至关重要, 可用于生物传感、材料分析和成像[1−7]. 但是, 完美磁导体在自然界中是不存在的. 基于这种情况, 人们提出了人工磁导体并将其应用于多个方面[8−12]. 通常, 结构化表面可以由谐振器阵列构成,例如设计在介电质层上的金属谐振器[13−15]. 然而,在高频波段下, 金属固有的欧姆损耗不可避免地导致磁镜的效率低下, 并限制了物质界面处电场的增强. 为了避免这种欧姆损耗, 具有在高频下以低吸收损耗以及能支持固有的强磁偶极共振的高折射率介电谐振器成为了磁镜设计的首选. 最近, 关于使用各种介电结构以获得磁镜的许多理论和实验工作已经被提出[16−20]. 实际上, 上述所有磁镜都具有由人造金属或介电微结构组成的光滑界面(即由相同尺寸的结构单元组成). 然而, 物质(例如小颗粒)通常不具有规则的形状, 这将会导致其在磁镜的光滑界面处与光的相互作用不足. 因此, 这种具有粗糙表面、与物质形状相匹配的磁镜设计在传感、成像以及界面处的光与物质的相互作用增强等应用中具有非常重要的意义.

另一方面, 为了模仿光频下金属纳米粒子所具有的局域表面等离激元, 基于结构完美电导体圆柱设计的人工局域表面等离激元概念也被人们提出[21].自此, 人们陆续进行了大量理论和实验工作来研究人工局域表面等离激元的电磁特性和应用[22−24].与二维人工表面等离激元结构相比, 具有有限厚度的三维结构圆柱不仅支持电偶极共振, 而且还支持磁偶极共振[25]. 最近, 本研究组也提出了一种空心的二维人工局域表面等离激元结构, 可以同时支持电偶极和磁偶极共振[26], 这种空心的人工局域表面等离激元结构具有类似于高折射率介电粒子中存在的Mie 共振性质[27]. 特别地, 可以通过裁剪结构几何参数自由地调节磁偶极和电偶极的谐振频率. 这些结果可能为设计具有粗糙表面的可调节磁镜以实现光与不规则物质之间的相互作用提供了一种思路.

在本文中, 提出了一种基于人工表面等离激元结构的粗糙磁镜. 首先研究了这种结构单元的电磁响应, 发现在该结构单元中可以支持强磁偶极子共振. 数值计算结果表明, 通过调整结构的螺旋度可以在不同外半径的螺旋结构中支持相同谐振频率的磁偶极子模式. 基于这种性质, 通过安排不同尺寸的结构单元排列组成的表面粗糙磁镜, 计算了这种粗糙磁镜的效率并与光滑磁镜作比较. 该结果提示, 这种磁镜可能会在低频中提供许多潜在的应用, 例如在生物传感、成像和界面处的光与物质相互作用增强方面.

2 人工表面等离激元结构设计及其电磁响应

图1(a)显示了二维的人工表面等离激元结构,该螺旋结构可通过周期地将具有对数螺旋线的螺旋金属条插入到介电圆盘中来构造. 在该模型中,空心螺旋结构的内半径和外半径分别用r和R表示. 此处, (ρ,θ)是极坐标,a和d= 2πR/N分别对应于金属条的宽度和周期, 其中N是金属条的数量. 结构中蓝色部分选择了一种折射率ng为3.4的材料(类似于硅), 黄色部分代表完美电导体, 整个结构被置于空气之中. 这种类似的螺旋结构已经被提出用来分析描述人工表面等离激元的电磁特性[28]. 在这里, 对数螺旋线的公式可以写成ρ=rexp[(log10(R/r)/θ0)θ], 螺旋槽的长度写为

其中θ0是对应于螺旋槽长度L的旋转角度, 在下文中θ0表示结构的螺旋度.

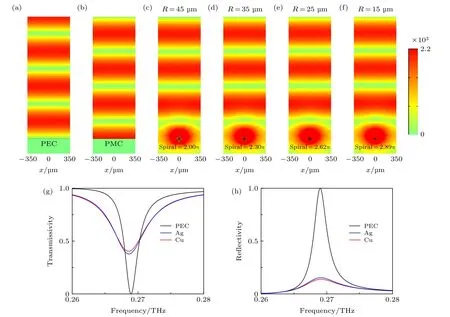
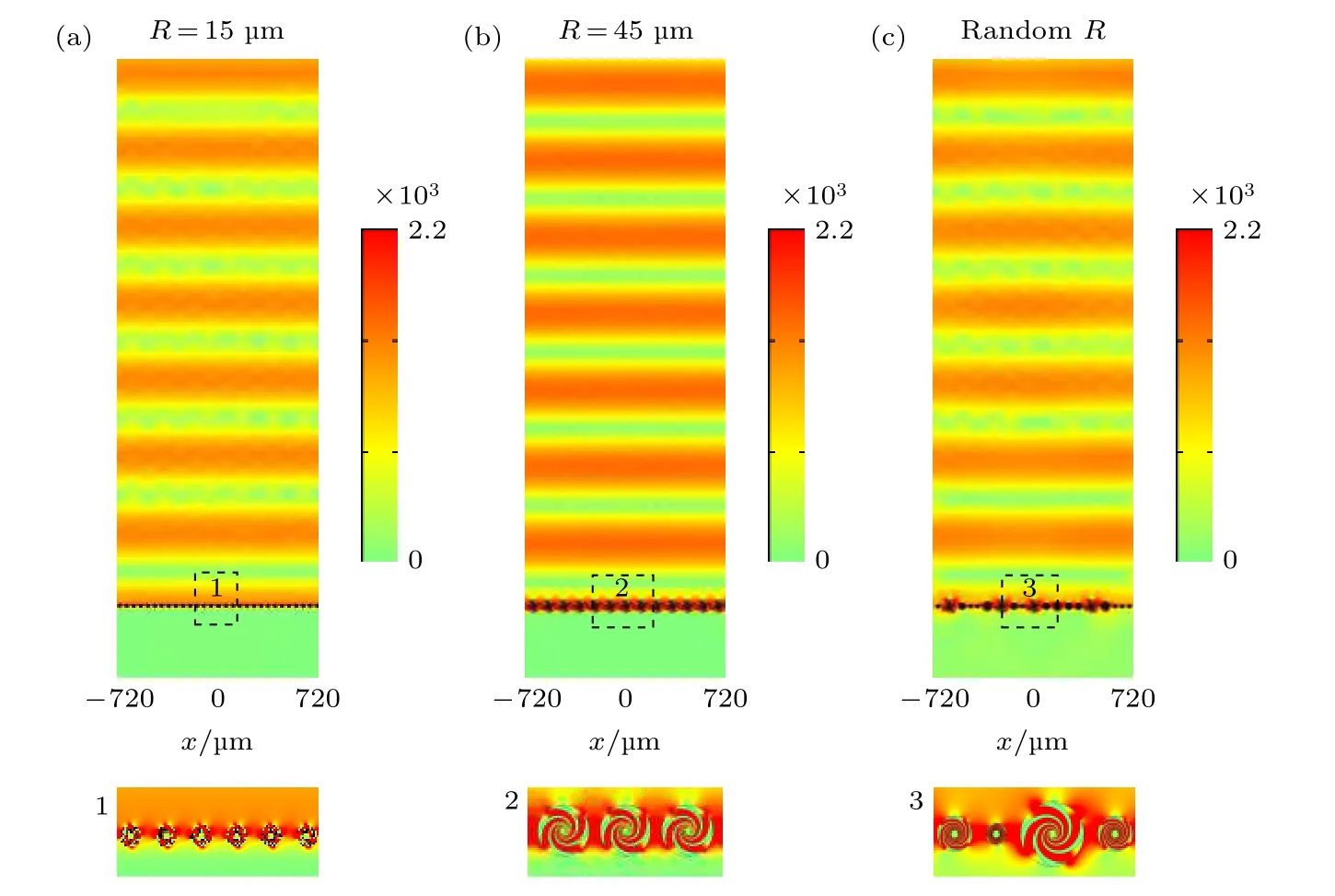
这些结构参数在图1(a)中已经标示. 这里, 选取的结构参数为R= 45 µm,r= 5 µm,a=d/3,N= 4,ng= 3.4,θ0=1.5π. 由于a

在图1(b)中, 使用商用软件COMSOL MULTIPHYSICS 计算了半径为R的螺旋结构的归一化散射截面, 这里的归一化散射截面为计算的总散射截面除以直径2R. 由于金属在较低频率下的行为类似于完美电导体, 在这里首先将人工表面等离激元结构的材料假定为完美电导体, 并计算了其散射截面(图1(b)中黑线). 另外从实际实验考虑, 还在图1(b)中给出了由实际金属银和铜材料制成的人工表面等离激元结构的归一化散射截面, 并分别用蓝色和红色实线表示. 从图1(b) 可以发现, 在结构的散射谱中有一个频率为f= 0.2684 THz 的共振峰. 为了进一步确认这些共振峰的模式, 给出了该频率下结构的近场分布Hz, 如图1(c)所示, 可以发现该共振峰对应着磁偶极模式.

图1 (a)人工表面等离激元结构示意图; (b)计算的由不同材料构成的人工表面等离激元结构的散射谱, 其中黑色曲线代表PEC, 蓝色曲线代表Ag, 红色曲线代表Cu; (c)图1(b)中的黑色实线对应的共振峰的近场模式HzFig. 1. (a) Schematic diagram of spoof surface plasmonic structure; (b)calculated scattering cross section spectrum of spoof surface plasmonic structure made of different materials, where the black curve represents PEC, the blue curve represents Ag and the red curve represents Cu; (c) near-field pattern H z for the resonant peak in the black solid line of (b).

接下来, 将讨论结构参数对磁偶极子谐振频率的影响. 图2 (a)中的绿色实曲线显示了当R=45 µm 并且其他结构参数不变时, 随着结构螺旋度从π 增加到3π 时谐振频率的变化, 此时可以发现谐振频率是下降的. 此外, 也发现当R从45 µm 依次降到15 µm 时, 对应于磁偶极子模式的谐振频率发生了蓝移. 产生这种现象的原因是结构参数的变化影响位移电流圆的大小, 从而导致磁偶极子共振频率的偏移. 同样, 在图2(b)和图2(c)中也研究了对于不同的内半径r与a/d的情况下, 磁偶极子模式的谐振频率与螺旋度之间的关系. 这些结果表明, 可以通过裁剪结构几何参数自由地调整与结构中磁偶极子相关的共振响应.

图2 (a)不同外半径下, 磁偶极子共振频率与螺旋度的关系, 图中的虚线和4 条实线的交点代表对应于相同共振频率的4 种结构; (b)不同内半径下, 磁偶极子共振频率与螺旋度的关系; (c) 对于不同的a/d, 磁偶极子共振频率与螺旋度的关系Fig. 2. (a) The magnetic dipole resonance frequency as the function of spiral degree for different outside radii. The intersection of the horizontal dotted line and the four solid curves in the figure represent the four structures corresponding to the same resonance frequency; (b) the relationship between the resonance frequency of magnetic dipole and spiral degree at different inner radii; (c) for different a/d, the relationship between the resonance frequency of magnetic dipole and spiral degree.

3 基于人工表面等离激元结构的平面磁镜

在上面的研究中, 主要讨论了人工表面等离激元结构的电磁响应特性, 结果表明, 该结构具有强磁偶极共振响应, 并且其共振频率可以方便地通过结构参数调控. 接下来, 将讨论如何通过人工表面等离激元结构阵列实现磁镜功能. 作为参考, 首先计算了平面波入射的完美电导体和完美磁导体产生的空间场分布(图3(a), (b)). 通过比较两图, 不难发现在完美电导体表面具有零电场强度, 但在完美磁导体表面却产生最大电场强度. 显然, 在完美磁导体界面处驻波的波节和波腹位置与完美电导体表面处的相比偏移了Δy≈λ/4, 也就是说二者之间近似相差π/2 的相位.

接下来, 将使用人工表面等离激元结构来演示所提出的磁镜. 图3(c)展示出了沿y方向的磁镜(R= 45 um,r= 5 um,a/d= 1/3,N= 4,θ0=2π)的电场大小分布. 图3(a)—(c)中给出的观测尺寸为700 µm × 2180 µm, 并且在x方向设置为周期性边界条件. 研究发现在结构表面产生了最大电场. 这一结果显然支持了本研究组的想法以及磁镜模型的有效性. 另外, 类似纳米结构(如蝴蝶结结构)缝隙的近场增强效应[29−31]也可以增强表面电场, 但是, 用来增强电场的纳米结构通常需要在底部设置一层基板(例如玻璃、石英、蓝宝石或硅)来制造, 因为独立的纳米间隙在结构上是很脆弱的. 其次, 相比纳米结构缝隙的近场增强效应,这种螺旋结构在共振频率的调节上具有很大的自由度并且可以在深度亚波长下操纵光.

磁镜可以有效消除常规介质界面处存在的电场的半波损耗, 从而使电场在边界附近增强. 由于它的这个优点, 磁镜被广泛运用于现代光学系统中. 为了实现小型化以便于集成和减少耗材, 需要寻找具有同样功能的超薄磁镜. 另外, 图2(a)中的结果表明能通过增加结构的螺旋度将具有相同谐振频率的磁偶极子支持在更小的外半径的螺旋结构中. 如图2(a)所示, 可以清楚地看到4 个不同的交点, 这些交点分别对应于不同结构的磁镜. 接下来, 依次将这4 种不同结构的磁镜绘制出来. 首先,图3(c)展示出了沿y方向的磁镜(R= 45 µm,r=5 µm,a/d= 1/3,N= 4,θ0= 2π)的电场大小分布. 然后, 将外半径减小到R= 35 µm, 同时将螺旋度增加到2.3π, 并在图3(d)中绘制出对应结构的电场. 接下来, 给出与第三个点相对应的场分布.此时, 在图3(e)中, 外半径减小到了25 µm, 螺旋度增大到了2.62π. 最后, 如图3(f)所示, 将结构的外半径调整为15 µm, 将螺旋度增大到2.89π.图4(c)—(f)显示了x-y平面上电场的近场分布. 从这些场分布中, 不难发现这些结构的模式分布是一致的, 并且这些磁镜的光谱分布也非常一致. 综上可得, 本研究组实现了具有相同功能的超薄磁镜,为实现光学仪器的小型化集成和减少耗材提供了一种潜在的可能.

图3 具有 (a)理想PEC 和(b)理想PMC 边界壁的电场|E|的分布; (c)−(f)在图2 中用“1” “2” “3”和“4”表示的4 种结构的电场|E|的分布; (g)−(h) 对于(c)中的结构参数, 用不同材料制成的结构的透射谱和反射谱Fig. 3. Snapshots of the electric field |E| for boundary walls with (a) the ideal PEC and (b) the ideal PMC; (c)−(f) snapshots of the electric field |E| for four structures of Fig. 2 denoted by “1” “2” “3” and “4”; (g)−(h) for the structural parameters of (c), transmission and reflection spectrum of structures made of different materials.

在上面的讨论中, 人工表面等离激元结构的材料由完美电导体制成. 然后, 为了更接近实验, 用实际金属代替了完美电导体, 并选择了两种特殊情况(铜和银)进行描述. 图3(g)和图3(h)中的黑色实线表示的是图3(c)中结构的透射谱和反射谱,同样, 用Ag(电导率6.3 × 1 07S/m)和Cu(电导率5.7 × 1 07S/m)代替完美电导体, 在图3(g)和图3(h)中分别用蓝色和红色实线表示. 值得一提的是, 用完美电导体材料是可以实现全反射的, 但是在使用金属材料时, 透射率和反射率之和是不为1 的, 这主要是由于金属的损耗造成的.

4 基于人工表面等离激元结构的粗糙磁镜

到目前为止, 研究仅限于平坦的表面(尽管对于整个结构而言, 单个结构之间存在间隙, 但其相对于整个表面而言可以忽略). 然而, 某些物质(例如小颗粒)通常不具有规则的形状, 并导致在磁镜的平坦界面处与光的相互作用不足. 因此, 需要在不同位置构造深度可调整的表面以满足与这些物质的充分相互作用.

图4(c)给出了本文所提出的这种粗糙磁镜,它是由图3中的4种结构随机排列组成的.当然,这些结构的大小不是固定不变的,可以根据物质的具体情况而定.为了表明粗糙表面不会扰乱电场分布,给出了两种大小不同的平滑表面.图4(a)和图4(b)分别是由29 个小结构(R=15µm,r=5µm,a/d=1/3,N=4,θ0=2.89π)和13个大结构(R=45µm,r=5µm,a/d=1/3,N=4,θ0=2π)组成的.这三种磁镜在平面波的作用下被激发.图4(a)—(c)显示了这些磁镜在x-y平面上的电场的近场分布,其总显示尺寸为1440µm×4680µm.为了更清楚地观察结构表面附近的电场分布,在每幅图的下方给出了每种磁镜表面的局部放大图(标记为1,2,3),分别对应于图4(a)—(c)中的黑色虚线框.结果表明,实现的这种粗糙磁镜,可以用来增强光与复杂物质之间的相互作用,它可以按照待测物体形状做调整设计,从而使得电场可以和物体充分相互作用.

图4 (a),(b)不同大小的光滑磁镜的电场|E|的分布及其局部放大图;(c)与(a)和(b)相同,只是用粗糙的磁镜代替光滑的磁镜Fig.4.(a),(b)Snapshots of the electric field|E|for sm ooth magnetic mirror of different sizes and their enlarged views;(c)sam e as(a)and (b)except rep lacing sm ooth magnetic mirror by rough magnetic mirror.

5 结 论

本研究在深亚波长范围内使用人工表面等离激元结构得到了磁镜.在这种结构中,可以通过激发其磁响应来实现磁镜.通过数值模拟发现磁偶极子共振与结构的外半径和螺旋度密切相关.通过同时调节两个参数,可以获得工作波长固定的超薄磁镜.为了在不均匀物质表面处实现足够的光与物质间的相互作用,提出了一种由不同尺寸的人工表面等离激元结构阵列组成的粗糙磁镜.这些结果对于增强光与复杂物质之间的相互作用具有非常重要的物理意义.