化学自突触的电导扰动诱导相干或随机双共振现象*

曲良辉 都琳 曹子露 胡海威 邓子辰

1) (西北工业大学数学与统计学院, 西安 710129)

2) (西北工业大学力学与土木建筑学院, 西安 710129)

3) (中原工学院理学院, 郑州 450007)

4) (复杂系统动力学与控制工信部重点实验室, 西安 710072)

神经元的自突触结构具有自反馈的作用, 神经递质量子形式的释放使得自突触的自反馈作用容易受到扰动, 本文重点研究了化学自突触的电导扰动对FHN 神经元电生理活动的影响. 首先, 恰当的化学自突触参数能够产生动力学行为的分岔现象, 诱导不同周期峰放电模式之间的转迁. 特别地, 自突触的自反馈功能会引起从混沌放电状态到周期的峰放电或准周期的簇放电状态的转迁. 其次, 基于神经递质释放的量子特征,借助放电频率和变异系数两个指标定量地研究自突触电导的随机扰动对神经元放电活动的影响. 数值结果表明自突触电导的扰动在自反馈的作用下能够改变离子通道的活性, 不仅提高FHN 神经元对外加激励信号的编码效率, 而且改变神经元放电活动的规则性, 诱导显著的相干或随机双共振现象, 其内在机制是电导扰动所引起的神经元系统不稳定的动力学分岔. 本文的研究进一步揭示了自突触结构对神经元放电活动自我调节的作用, 有待为生理操控自突触结构提供理论参考.

1 引 言

大脑神经系统由神经元和神经胶质细胞共同构成, 各个神经元之间通过突触实现神经信息的传递和通信. 特别地, 一个神经元的轴突可以和自身的树突或胞体发生突触连接, 从而形成一种特殊的自突触结构. van der Loos 和Glaser[1]在1972 年首次公开报道了这种突触结构. 目前, 已经证实许多脑区都存在自突触结构, 且自突触也遵循神经系统工作的结构原理[2,3]. 关于自突触的成因目前主要有两种解释, 一是自突触结构是由神经损伤或信号传输受阻所致, 是神经元自适应和自我调节的结果[4], 二是通道噪声的存在导致了自突触结构的发生[5], 这些解释还有待深入的生理实验进行证实.

生理上, 自突触分为化学自突触和电自突触两种类型, 能够提供一种自反馈的作用, 体现了神经元过去状态对当前状态的影响. 数学上, 自突触功能通常用一个时滞反馈项进行刻画, 其作用大小主要由自突触电导和延迟时间两个参数决定[6−9]. 由于自突触结构的特殊性, 已经吸引了许多学者对其进行研究. 对于单个神经元系统来说, 自突触功能主要是调控神经元的放电行为, 能够引起神经元放电模式的转迁. 通常, 电自突触正反馈能够提高神经元的兴奋性, 而负反馈抑制神经元的放电活动,可以引起从簇放电到峰放电的状态转迁[10−13]. 无论是弱突触输入还是强突触输入电流, 自突触延迟时间能引起神经元产生多相干共振现象[14,15], 并且具有自突触结构的神经元能够有选择性地输出频率一定的放电脉冲序列, 起到低通或带通滤波器的作用[16]. 另外, 自突触结构还能够改变神经元系统动力学行为的分岔类型[17], 且恰当的时滞时间能够使得神经元信息传输的能力和能量效率最大[18].对于神经元网络, 自突触结构可以作为节拍器或控制器对网络的放电活动进行调控, 不仅能够提高网络的同步性, 而且还能改变神经元网络时空斑图的演化规律[19−27]. 作为节拍器的电自突触能够使得二维最近邻耦合的神经元网络产生靶波或螺旋波[28,29]. 特别地, 电自突触的负反馈能够抑制网络中波的传播, 而正反馈可以通过诱导靶波而实现网络放电活动的调控[30]. 当自突触时滞为神经元自身振荡周期的整数倍时, 自突触时滞会引起神经元网络产生多相干共振或多随机共振现象[15,31−33],并且在STDP(spike-timing-dependent plasticity)突触可塑性的条件下还能够增强突触噪声引起的多相干共振现象和诱导显著的同步转迁行为[34].另外, 自突触结构能够对Newman-Watts 小世界的神经元网络中的弱局部周期信号的传播进行有效的调节[35], 且在电磁感应的作用下, 化学自突触能诱导两个耦合的神经元从混合振荡模式到周期放电模式的转迁[36]. 进一步地, 自突触的自反馈作用依赖于自突触结构在神经元系统中所处的位置[2],其恰当的位置分布能够有效地提高神经元网络的同步性[37], 且少量的自突触结构可以通过诱导半环形靶波恢复由相位噪声中断的神经信号的传播[38].

神经元系统中的自突触结构具有如此丰富的计算神经特征, 是否可以考虑生理操控自突触结构用来治疗某些器质性的神经疾病呢? 基于这样的目的, 本文选取FHN 神经元为研究对象, 探讨化学自突触电导的扰动对神经元系统动力学行为的影响. 首先, 研究FHN 神经元系统的动力学行为对外加激励的响应特征. 其次, 讨论化学自突触的两个参数所引起的动力学分岔现象. 最后, 借助放电频率和变异系数两个指标研究化学自突触电导的随机扰动对神经元放电活动的影响, 并探讨电导扰动所引起的双共振现象的动力学机制.

2 数学模型及其动力学分析

考虑神经药物或毒素对神经元离子通道活性的调节作用, 可以得到具有化学自突触结构的FHN(FitzHugh-Nagumo)神经元模型为[39,40]

其中

式中, 变量V表示膜电压,W表示恢复变量. 对应着神经药物或毒素对神经元离子通道活性调节作用的外加激励可以表示为Iext=Acos(2πft) , 其中A和f分别为激励的振幅和频率.Iaut为自突触电流, 本文考虑快速阈值调制方式的化学自突触. 由于化学神经递质释放的量子形式[41−43], 自突触电导会产生随机扰动, 此时自突触电流可由(3)式表示, 其中gc为化学自突触电导,τ为延迟时间,Vsyn为突触反转电位, 应用中Vsyn=1.2 代表兴奋性突触, 而Vsyn=-0.2 代表抑制性突触, 并且取定比率参数λ=2.0 和突触阈值θ=0.4 . 这里自突触电导扰动ξ(t) 采用高斯白噪声的形式, 其统计特性满足:〈ξ(t)〉=0,〈ξ(t)ξ(t′)〉=2Dδ(t-t′),其中D为噪声强度,δ(·) 为 狄拉克δ函数. 另外,a,b,ε为系统参数, 文中取定a=0.1,ε=0.01,c=2.0[40].

对FHN 神经元施加周期性的外加激励Iext=Acos(2πft), 初步探讨无自突触结构时该神经元系统对外加激励的动力学响应. 文中所有数值实验的时间步长为 Δt=0.01,初值为V0=-0.2 和W0=-0.2, 并且默认神经元脉冲放电活动的膜电压的临界值为0.6. 从图1(a)可以看出, 由于第二类神经元可兴奋性的特点, 具有较小振幅的外加激励无法使神经元的膜电压达到放电阈值, 从而导致FHN 神经元不会产生峰放电活动. 另一方面,外加激励的周期性振荡能够对神经元的放电活动进行有效的调节, 其振荡的性质往往有助于神经元产生脉冲放电活动. 例如, 当振幅A=0.6 和频率f=0.0时, 神经元的膜电压处于高位的静息态, 即生理上的去极化阻塞[44,45]; 但在A=0.6 的条件下,只要频率f∈[0.1,34.8] , 神经元就能产生脉冲放电活动. 进一步地, 如果频率f超过临界值34.8, 那么神经元就不再出现脉冲放电现象, 这主要是因为外加激励频繁的振荡影响了离子的跨膜运动过程, 从而导致了不充分的去极化和极化过程, 致使神经元的膜电压不会出现超射和超极化现象.

从图1(b)知, 周期激励的频率会改变神经元系统的动力学行为. 当A=0.6 时, 对于频率f的某些不连续的取值, 神经元系统的最大Lyapunov 指数明显大于零, 这说明神经元会出现混沌的放电活动, 如图2 所示. 由此可知, 在外加激励的作用下,无自突触结构的FHN 神经元系统的动力学行为会发生变化. 神经元系统对周期性的外加激励的响应呈现非线性的变化特点, 其放电频率存在跳变现象, 这主要是神经元放电活动内在的频率和外加激励的振荡频率相互作用的结果. 此外, 外加激励的周期性变化还能够诱导周期态和混沌态之间的转迁, 体现了FHN 神经元对外加激励的敏感性.

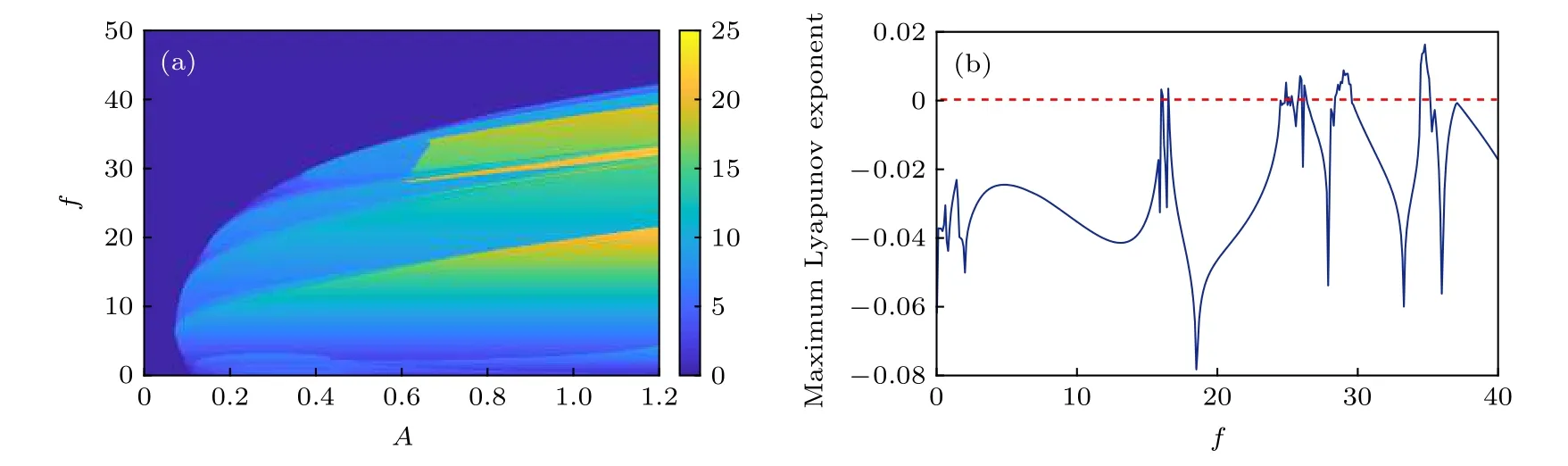
图1 FHN 神经元系统的脉冲放电频率(a)及其最大Lyapunov 指数(b)对周期振荡的外加激励的依赖关系示意图, 其中(b)中周期激励的振幅为A=0.6Fig. 1. Dependence of (a) spike discharge frequency and (b) maximum Lyapunov exponent on external periodic excitation, where the amplitudes of periodic excitation are A=0.6 in the subfigure (b).

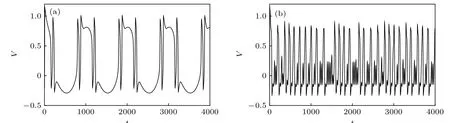
图2 外加周期激励的作用下FHN 神经元放电活动的时间历程图 (a) A=0.6 , f=1.0 ; (b) A=0.6 , f =29.0Fig. 2. Sampled time series of neuronal membrane potentials under different periodic excitation: (a) A=0.6 , f=1.0 ; (b) A=0.6 ,f =29.0.

3 化学自突触诱导动力学分岔

作为大脑神经系统普遍存在的一种生理结构,自突触应该是神经系统自然进化的结果. 由于先天遗传和后天发展的不同, 不同个体大脑神经系统中的自突触结构的功能参数存在差异, 从而对神经电生理活动具有不同的调控作用. 从图3 可以看出,当外加激励Iext=0.05 时, FHN 神经元处于静息态, 此时对其激活兴奋性的化学自突触结构, 那么恰当的自突触参数能够诱导神经元产生脉冲放电活动, 并且自突触参数对神经元放电频率的影响存在显著的跳跃现象, 具有非线性的变化特点. 在外加激励Iext=0.6 的条件下, 抑制性的化学自突触使得处于高位静息态(去极化阻塞)的神经元恢复周期性的脉冲放电活动. 不管是兴奋性的还是抑制性的化学自突触, 都存在一个敏感的突触参数的取值区域, 使得FHN 神经元能够产生比较频繁的脉冲放电活动, 体现了神经元放电活动对自突触参数的敏感性. 进一步地, 需要研究自突触参数的变化对神经元放电活动的峰峰间期序列的影响. 图4 显示的是神经元脉冲放电的峰峰间期序列(ISI)的变化分别对自突触电导和延迟时间的依赖关系, 其中固定的自突触参数分别为延迟时间τ=30.0 和突触电导gc=0.3 . 对于Iext=0.05 , 随着自突触电导或延迟时间的增大, 神经元放电的峰峰间期序列在单周期、双周期和三周期之间变化, 对应于神经元的放电活动在静息、周期峰和周期簇三种放电状态之间的转迁, 这说明兴奋性的自突触结构能够显著地改变神经元的放电行为, 诱导比较复杂的动力学分岔现象. 对于Iext=0.6 , 随着自突触电导或延迟时间的增大, 自突触的抑制性能够恢复离子通道的活性, 从而使得处于去极化阻塞状态的神经元产生周期性的峰放电活动, 并且只有当延迟时间τ≥52.6时自突触功能才能诱导比较明显的峰峰间期分岔现象, 如图4(d)所示.

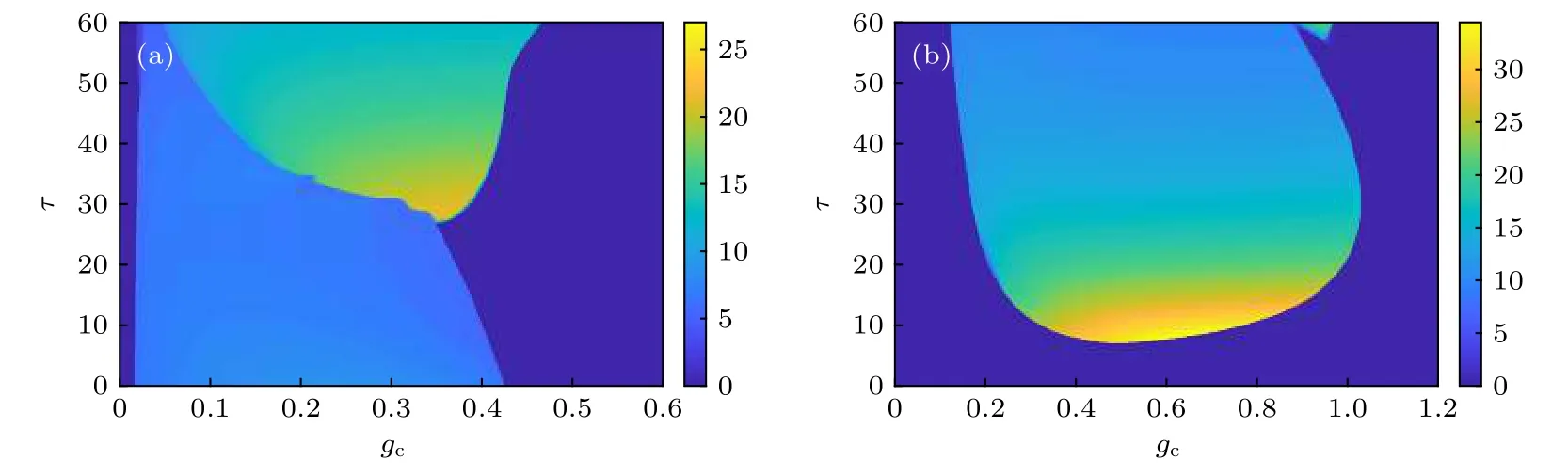
图3 不同外加激励和突触反转电位条件下FHN 神经元脉冲放电的频率对自突触功能两个参数的依赖关系示意图 (a)Iext =0.05 , V syn =1.2 ; (b) I ext =0.6 , Vsyn =−0.2Fig. 3. Dependence of spike discharge frequency of FHN neurons on two autaptic parameters under different applied excitation and synaptic reversal potential: (a) I ext =0.05 , V syn =1.2 ; (b) I ext =0.6 , V syn =−0.2 .

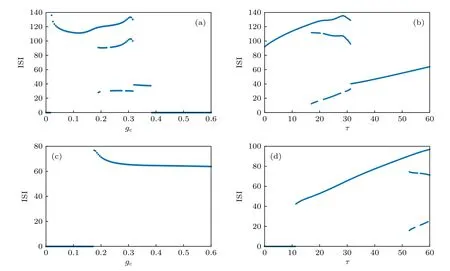
图4 FHN 神经 元脉冲 放电的 峰峰间 期对不 同 的自突 触结构 参数的 依赖关 系示意 图 (a) I ext =0.05 , τ=30.0 , V syn =1.2 ;(b) I ext =0.05 , g c =0.3 , V syn =1.2 ; (c) I ext =0.6 , τ=30.0 , V syn =−0.2 ; (d) I ext =0.6 , g c =0.3 , Vsyn =−0.2Fig. 4. Dependence of neuronal firing inter-spike intervals on different autaptic parameters: (a) I ext =0.05 , τ=30.0 , V syn =1.2 ;(b) I ext =0.05 , g c =0.3 , V syn =1.2 ; (c) I ext =0.6 , τ=30.0 , V syn =−0.2 ; and (d) I ext =0.6 , g c =0.3,V syn =−0.2 .

选取自突触参数gc=0.3 和τ=30.0 , 图5(a),(b)分别显示了兴奋性和抑制性自突触功能激活后FHN 神经元放电活动的变化过程, 直观地揭示了化学自突触功能的兴奋性和抑制性对神经元放电活动的不同的调控作用. 另外, 在振荡的外加激励作用下, FHN 神经元能够呈现混沌的放电状态,如图2(b)所示, 那么化学自突触结构是否能够对这种混沌的放电活动进行有效的调控呢? 从图5(c),(d)可以看出, 在自突触兴奋性的自反馈作用下,神经元能够从混沌的放电状态分别转迁为周期的峰放电或准周期的簇放电状态, 这是自突触功能所引起带电离子跨膜运动变化的结果. 值得注意的是, 对于外加激励的振幅A=0.6 和频率f=16.0的这种情况, 兴奋性的自突触结构不仅改变神经元放电脉冲的振荡幅值, 而且对神经元放电状态的调控非常缓慢, 从混沌状态转迁到周期的峰放电状态大约持续了1500 个时间单位, 这应该是神经元内在活动的周期、外加激励的周期和自突触功能的延迟时间三个时间尺度不匹配的结果.

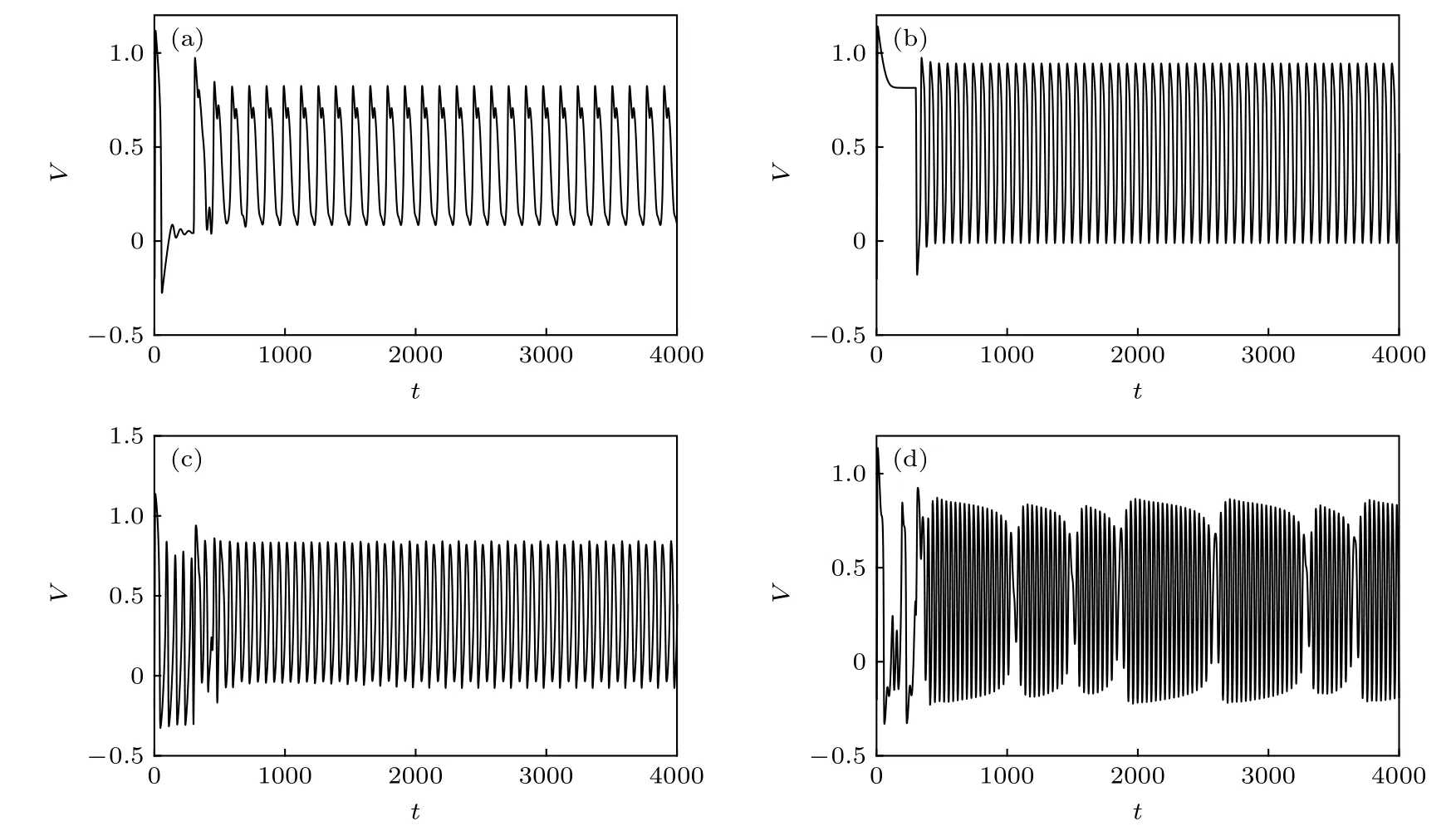
图5 具有自突触结构的FHN 神经元放电活动的时间历程图, 其中自突触参数 g c =0.3,τ=30.0,且自突触功能在 t=300 时被激活 (a) A=0.05 , f=0 , V syn =1.2 ; (b) A=0.6 , f=0 , V syn =−0.2 ; (c) A=0.6 , f=16.0,V syn =1.2 ; (d) A=0.6 , f=29.0 , Vsyn =1.2Fig. 5. Sampled time series of neuronal membrane potentials under excitatory or inhibitory autaptic function, where g c =0.3 ,τ =30.0 , and the autaptic function is activated at t=300 : (a) A=0.05 , f=0 , V syn =1.2 ; (b) A=0.6 , f=0 , V syn =−0.2 ;(c) A=0.6 , f=16.0 , V syn =1.2 ; (d) A=0.6 , f=29.0 , V syn =1.2 .

总之, 化学自突触结构能够对FHN 神经元的电生理活动进行有效的调控, 其中兴奋性的自突触能够诱导静息态的神经元产生周期性的脉冲放电活动, 而抑制性的自突触能够诱导从高位静息态到峰放电状态的转迁. 特别地, 在化学自突触的自反馈作用下, 恰当的自突触参数能够使得神经元的动力学行为产生比较复杂的分岔现象, 体现了神经元的电生理活动对自突触参数的敏感性. 进一步地,自突触结构还能够对处于混沌放电状态的神经元进行调控, 可以诱导周期的峰放电或准周期的簇放电活动.

4 自突触电导扰动诱导共振现象

由于神经元突触结构中神经递质释放的量子特征, 化学自突触的自反馈功能容易受到诸如电磁场、热噪声和神经药物等因素的干扰. 为了研究自突触电导的随机扰动[46]对FHN 神经元放电活动的影响, 这里选取神经元的放电频率和峰峰间期序列的变异系数两个度量指标进行统计分析, 其中峰峰间期序列的变异系数定义如下:

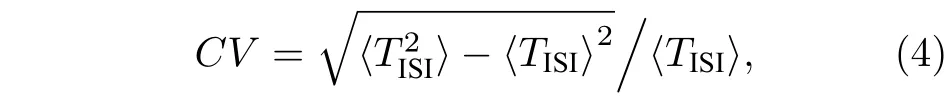
其中,TISI表示神经元膜电压的峰峰间期序列,〈TISI〉表示峰峰间期序列的平均值, 而则表示峰峰间期序列的均方值[15,47]. 通常, 较小的变异系数对应于神经元比较规则的放电行为. 由于自突触电导的随机性, 这里采用二阶随机的Runge-Kutta方法进行数值计算, 并且应用40 次取平均的方法进行统计分析[8,48].

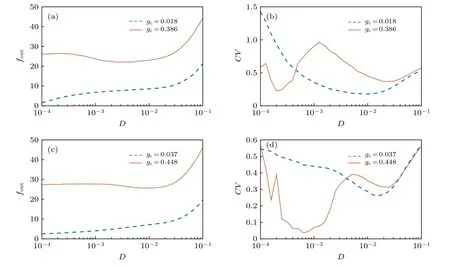
图6 在自突触电导随机扰动的作用下FHN 神经元的放电频率和峰峰间期序列的变异系数对噪声强度的依赖关系示意图 (a), (b) A=0.05 , f=0 , τ=30.0,V syn =1.2 ; (c), (d) A=0.05 , f=10.0 , τ=30.0 , Vsyn =1.2Fig. 6. Dependence of spike discharge frequency and coefficient of variation on noise intensity under disturbance of autaptic conductance, where (a), (b) A=0.05 , f=0 , τ=30.0 , V syn =1.2 ; (c), (d) A=0.05 , f=10.0 , τ=30.0 , V syn =1.2 .

图6分别显示了FHN 神经元的放电频率和峰峰间期序列的变异系数随着噪声强度的增大所呈现的变化趋势, 其中选取恒定和周期两种类型的激励进行对比分析. 无论是恒定激励还是周期激励,如果自突触电导不发生随机扰动, 那么在图6 所提供的自突触参数的条件下, FHN 神经元将处于静息态或次阈值振荡的状态. 相反地, 如果自突触电导受到高斯白噪声形式的随机扰动, 那么自突触结构能够激发FHN 神经元产生脉冲放电活动. 当噪声强度D<0.01 时, 神经元的放电频率会随着噪声强度的增大呈现比较显著的非线性的变化特点. 随着D的持续增大, 神经元的放电频率几乎保持线性递增的变化趋势, 如图6(a), (c)所示, 体现了随机扰动对神经元放电活动积极的促进作用. 另一方面, 无论是恒定激励还是周期激励, 当自突触电导均值比较小时, 随着D的增大, 神经元放电的峰峰间期序列的变异系数均呈现先减小后增大的变化趋势, 如图6(b), (d)所示, 这表明恰当的噪声强度诱导了比较显著的相干共振或随机共振现象. 然而, 当自突触电导均值比较大时, 峰峰间期序列的变异系数会经历两次先减小后增大的变化过程, 这对应着双共振现象. 以外加激励Iext=0.05 为例, 深入分析可知, 此时双相干共振现象产生的潜在机制是在随机扰动的作用下自突触电导发生相应的振荡, 较小强度的噪声使得自突触电导主要在0.386附近的一个小邻域内变化, 导致神经元放电活动只在静息态和单周期的峰放电状态之间跃迁, 如图4(a)所示, 从而产生了第一次显著的相干共振现象; 当噪声强度比较大时, 自突触电导会在以0.386 为中心的一个更大的区间内变化, 导致神经元的动力学行为出现比较复杂的分岔现象, 对应的神经元的放电活动可能在静息态、单周期、三周期和二周期的峰放电状态之间跃迁, 从而为第二次相干共振的发生提供了可能性. 类似地, 对于外加激励Iext=0.6 ,自突触电导引起的峰峰间期的变化相对简单, 如图4(c)所示, 根据上述共振现象产生的机制可知,自突触电导扰动也能诱导共振现象, 但无法诱导双共振现象.

为了进一步探讨自突触电导的扰动对神经元放电活动的影响, 图7 给出了在不同的噪声强度下FHN 神经元放电活动的时间历程图, 其中A=0.05 ,f=10.0,τ=30.0,Vsyn=1.2 . 对于gc=0.037, 当自突触电导无扰动时, 神经元处于阈下振荡状态; 若自突触电导存在扰动, 随着电导扰动的噪声强度增大, 神经元出现脉冲放电现象, 且当D=0.016时神经元出现比较频繁且规则的脉冲放电活动, 这对应着电导扰动所诱导的随机共振现象, 如图7(b)所示, 这表明恰当的电导扰动有利于促进神经元对外加激励信号的编码效率. 对于较大的自突触电导gc=0.448 , 当自突触电导无扰动且在t=300 被激活后, 神经元会从阈下振荡状态转迁到高位振荡状态, 其原因是自突触电流改变了神经元系统两条零斜线的位置关系; 若自突触电导存在扰动, 当D=0.0007 时, 神经元放电的峰峰间期序列的变异系数取得最小值, 此时神经元呈现频繁且规则的脉冲放电活动, 如图7(c)所示. 当噪声强度进一步增大到D=0.005 时, 从带电离子跨膜运动的角度分析, 电导扰动引起的自反馈功能的强振荡性使得细胞膜对离子的通透性产生快速变化, 致使神经元的放电活动出现不彻底的去极化和复极化过程, 从而降低了神经元脉冲放电活动的规则性, 如图7(d)所示.

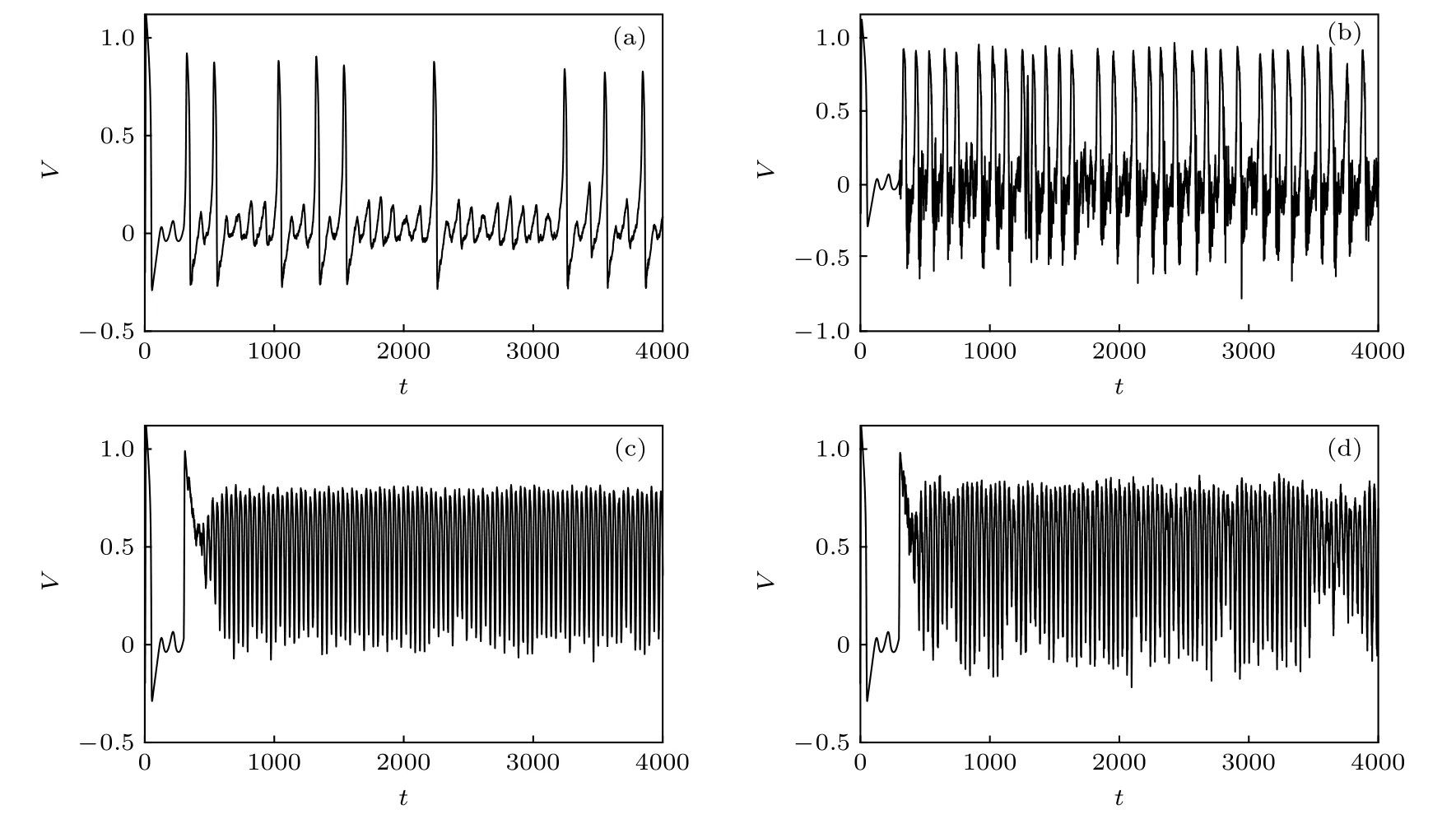
图7 具有自突触结构的FHN 神经元放电活动的时间历程图, 其中 A=0.05 , f=10.0,τ=30.0,V syn =1.2 , 且自突触功能在 t=300 时 被 激 活 (a) g c =0.037 , D=0.0001 ; (b) g c =0.037 , D=0.016 ; (c) g c =0.448 , D=0.0007 ; (d) g c =0.448 ,D= 0.005Fig. 7. Sampled time series of neuronal membrane potentials under autaptic function , where A=0.05 , f=10.0,τ=30.0 ,Vsyn =1.2 , and the autaptic function is activated at t=300 : (a) g c =0.037 , D=0.0001 ; (b) g c =0.037 , D=0.016 ; (c) gc =0.448 , D=0.0007 ; (d) g c =0.448 , D=0.005 .

综上可知, 自突触电导的随机扰动能够对神经元的放电行为产生比较大的影响, 一方面, 当噪声强度介于0.01 和0.10 之间时, 噪声强度越大, 神经元的放电频率也越大, 并且二者近似呈现线性关系, 由此表明了电导扰动对神经元信息编码的促进作用; 另一方面, 自突触电导的随机性在自反馈的作用下对离子通道的活性产生较大影响, 能够改变神经元放电活动的规则性, 不仅使得神经元的动力学行为产生显著的相干共振或随机共振现象, 而且还能产生双相干共振或双随机共振现象, 丰富了FHN 神经元的动力学行为.

5 结 论

为了探讨利用自突触结构治疗神经疾病的可行性, 以FHN 神经元为研究对象, 系统研究化学自突触结构对神经元系统的动力学行为的自反馈作用.

首先, FHN 神经元对基于神经药物对离子通道活性调节的外加周期激励比较敏感. 该周期激励会改变FHN 神经元系统的动力学行为, 不仅引起神经元放电频率的不连续变化, 而且还能诱导混沌的放电状态. 其次, 化学自突触结构对FHN 神经元电生理活动的自反馈作用依赖于突触特征, 其中兴奋性的自突触诱导静息态的神经元产生周期性的脉冲放电活动, 而抑制性的自突触诱导从高位静息态到峰放电状态的转迁. 进一步地, 在自反馈的作用下, 自突触的两个结构参数引起神经元的动力学行为出现分岔现象, 诱导不同周期峰放电模式之间的转迁. 特别地, 自突触结构可以把神经元从混沌的放电状态调节到周期的峰放电或准周期的簇放电状态.最后,基于神经递质量子式释放的自突触电导的随机扰动在自反馈的作用下影响带电离子的跨膜运动过程,从而改变FHN神经元对外加激励的响应能力.随着电导扰动的噪声强度的增大,神经元的脉冲放电频率也越来越大,体现了噪声对FHN神经元信息编码的促进作用.同时,自突触电导的扰动可以改变神经元放电活动的规则性,不仅诱导显著的相干或随机共振现象,而且还能产生相干或随机双共振现象,从而使得神经元具有更丰富的生理现象.

作为神经系统广泛存在的一种生理结构,自突触在神经疾病治疗方面具有潜在的应用前景.上述研究充分表明了化学自突触结构可以有效地改变神经元系统的动力学行为,能够为自突触结构的生理应用提供理论指导.此外,依据自突触结构对神经元自身的反馈作用,可以构造具有局部自反馈的递归脉冲神经网络,应用突触可塑性的学习规则有望提高机器学习的能力.