轴向各向异性地-井瞬变电磁三分量响应特征

郭建磊，姜 涛，郭 恒，宁 辉，刘 航

(1.中煤科工集团西安研究院有限公司，陕西 西安 710077; 2.长安大学 地球物理场多参数综合模拟实验室(中国地球物理学会重点实验室),陕西 西安 710054)

0 引 言

随着瞬变电磁法勘探逐步向大深度、高精度方向发展[1-3]，地-井瞬变电磁法获得了快速发展。该方法采用地面布设发射回线、钻孔采集三分量磁场数据的工作装置(图1)进行深部探测，具有受地面电磁或人为干扰小、响应信号强等优势，突破“一孔之间”并实现“一孔多用”，在深部找矿、寻找地质构造等方面具有不可替代的优势[4]。20世纪90年代，该方法被广泛应用于金属矿勘查领域且效果显著，加拿大、澳大利亚及苏联学者在理论、仪器等方面均进行了系统研究[5-7]。近几年，国内相关研究呈现出“井喷”态势，研究领域主要集中在正演模拟[8-9]、处理解释[10-11]和实际应用[12-13]等方面。

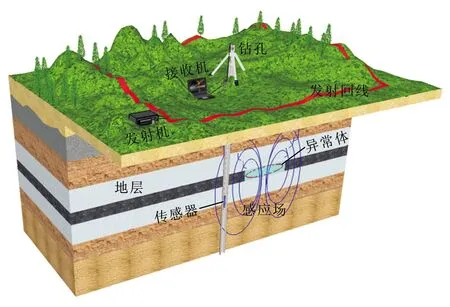
图1 地-井瞬变电磁法探测示意图

王鹏通过对地-井瞬变电磁异常体感应涡流场三分量响应特征、三分量响应的空间指向性以及浮动系数空间交汇算法和最小二乘反演算法进行研究，实现地-井瞬变电磁法的异常体三维空间定位技术[11]；武军杰研究了电性源地-井瞬变电磁三分量响应特征，发现电性源三分量响应曲线对于电性界面、异常体具有良好的反映，同时基于反函数定理实现电性源地-井瞬变电磁全域视电阻率定义并验证提出全域视电阻率能基本可靠反映地下信息，最后对磁性源地-井和地-空瞬变电磁建立空-井联合解释方法，野外实测资料数据处理表明该方法快速、可靠[10]；姚伟华等对地面布设发射回线、井下工作面水平钻孔中进行三分量接收的超前探测工作装置形式进行了三维正演模拟，并在地面进行了地孔瞬变电磁超前探测方法的相似性试验[14]；范涛等将地-井瞬变电磁法借鉴到煤矿井下巷道超前探测中，在煤矿巷道掌子面激发、掌子面钻孔中进行接收，对上述工作方式进行了三维数值模拟和物理模拟研究，并基于水平分量和垂直分量数据判断异常体深度、所在象限、方位角及径向距离，最终利用总场拟地震处理方法实现钻孔径向拟电阻率反演成像[15]。

目前，地-井瞬变电磁的相关研究均是将地层假设为各向同性介质，当遇到具有明显层理的沉积岩或裂隙发育地区，导电大地不同方向的导电能力发生变化，地下介质表现出宏观电导率各向异性[14,16-23]。周建美等基于有限体积法实现双轴各向异性瞬变电磁三维正演，发现水平方向电导率各向异性严重影响瞬变电磁垂直分量磁场响应[24]；刘亚军等基于有限体积法实现瞬变电磁任意各向异性三维正演，发现主轴水平方向各向异性严重影响瞬变电磁垂直分量磁场响应，且倾斜各向异性比水平各向异性影响更为严重[25]；程久龙等基于时域有限差分算法研究地层各向异性对矿井瞬变电磁的影响特征，并结合实例进行说明[26]。前人研究结果均说明介质各向异性特性会严重影响瞬变电磁响应，尤其是三维各向异性异常体的影响会更为突出[27]。基于各向同性模型的传统成像及反演成像技术不再适用于各向异性数据的处理解释,上述研究均是电导率各向异性对瞬变电磁垂直分量的影响，且目前地-井瞬变电磁法主要接收三分量数据[28]，因此，需要研究介质的电各向异性对地-井瞬变电磁三分量磁场响应的影响，为精细化地质探测提供指导依据。

本文基于时域有限差分算法[29-30]，通过引入轴向电导率张量构建各向异性电磁场控制方程，推导无源和有源轴向各向异性电场三分量迭代公式，其中磁场分量的迭代计算公式与各向同性磁场迭代计算公式一致，以电流密度的形式加入各向异性麦克斯韦(Maxwell)方程组的安培环路定理实现电流源的加载，实现轴向各向异性三维瞬变电磁三分量正演。通过与各向异性半空间模型一维解析结果对比验证算法的准确性，后续分别建立各向异性三维模型进行正演模拟，研究地-井瞬变电磁三分量磁场响应特征。

1 各向异性瞬变电磁有限差分正演原理

1.1 正演算法原理

在各向异性、有耗、非磁性、无源媒质中的麦克斯韦方程组[26]分别表示为

(1)

(2)

(3)

(4)

地球物理勘探一般忽略位移电流作用，为了构成显式的时间迭代格式，满足三维时域有限差分计算要求，加入人工虚拟介电常数项(γ)，式(2)变换为

(5)

采用经典Yee晶胞格式对计算区域进行网格剖分(图2)，电场分量位于六面体的棱边中心点，磁场分量位于六面体的面中心点，每一个电场(磁场)分量均被相应的4个磁场(电场)分量所包围，电场分量和磁场分量在时间轴上交替采样(图3)。

i、j、k分别为x、y、z方向网格剖分的节点；Ex、Ey、Ez分别为x、y、z方向上的电场分量；Hx、Hy、Hz分别为x、y、z方向上的磁场分量

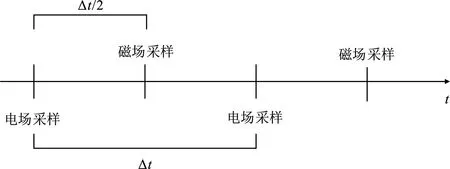
Δt为时间间隔

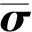
(6)

式中：σx、σy、σz分别为x、y、z方向上的电导率。

瞬变电磁正演主要依靠低频成分，必须将磁场的散度方程显示的包含进去，因此，在直角坐标系中得到麦克斯韦方程各分量的形式为

(7)

(8)

式中：Bx、By、Bz分别为x、y、z方向上的磁感应强度分量。

以差分代替微分对麦克斯韦方程进行求解，空间离散采用后向差分，时间离散采用中心差分，采用非均匀网格形式进行模型剖分[30]，可以得到电导率各向异性下电场强度的迭代表达式[式(9)～(11)]。

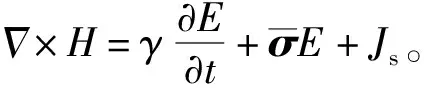
回线源一般放置xOy平面，因此，方程中仅存在x、y方向上的源电流密度项(Jsx、Jsy)。在直角坐标系中加入电流密度展开后，将发射回线所在网格按照差分格式正常离散，就可以得到有源区域网格电场迭代形式[式(12)、(13)]。

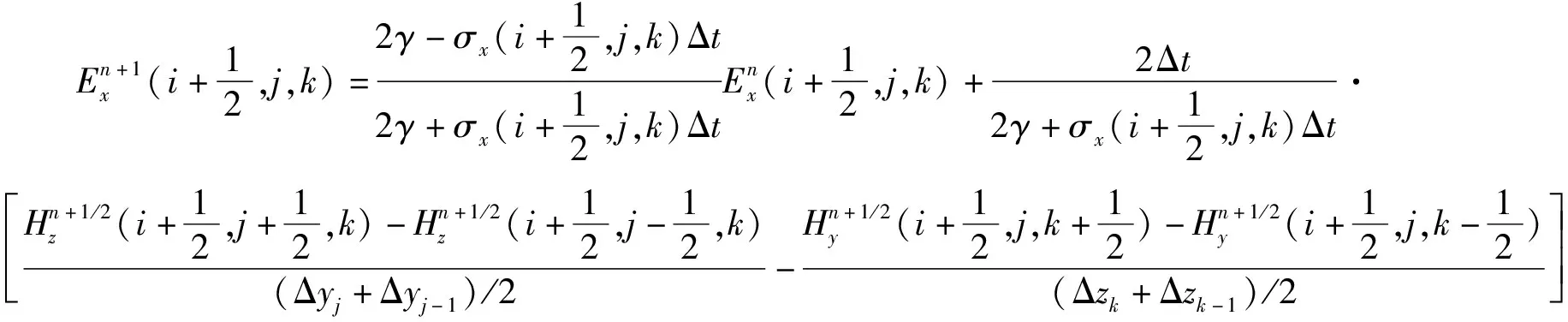
(9)

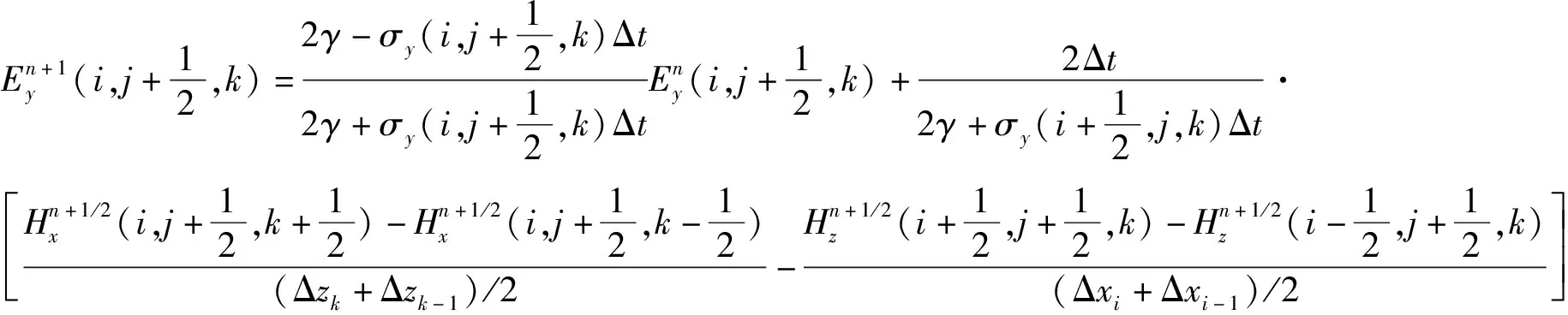
(10)

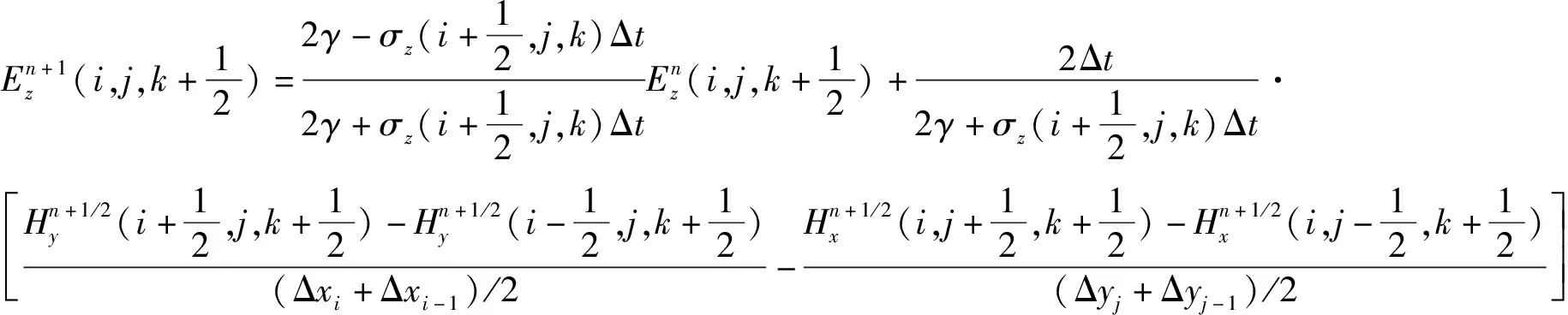
(11)

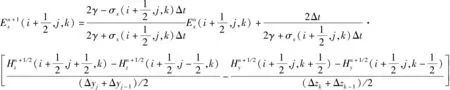
(12)

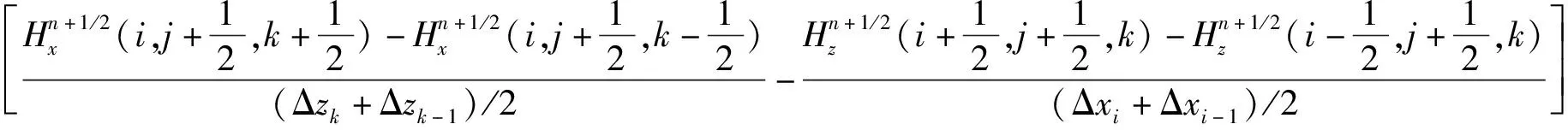
(13)

式中：Δx、Δy、Δz分别为剖分网格的长度。

磁场迭代公式不包含电导率项，因此，各向异性磁场迭代公式与各向同性迭代公式相同[30]。

瞬变电磁法是宽频带勘探方法，加载梯形波作为激发源，利用正、余弦开关函数对梯形波的上升沿和下降沿进行特殊处理，避免两个不可导尖点对差分代替微分运算所造成的冲击作用[30]。选用第一类边界条件，即在6个边界面上将电场和磁场分量全部强制赋0，计算过程中就需要满足时间域和空间域的稳定性条件，即Courant稳定性条件，以保证电磁场传播的因果关系。该稳定性条件为

(14)

式中：ν为电磁波的相速度。

1.2 正演算法验证

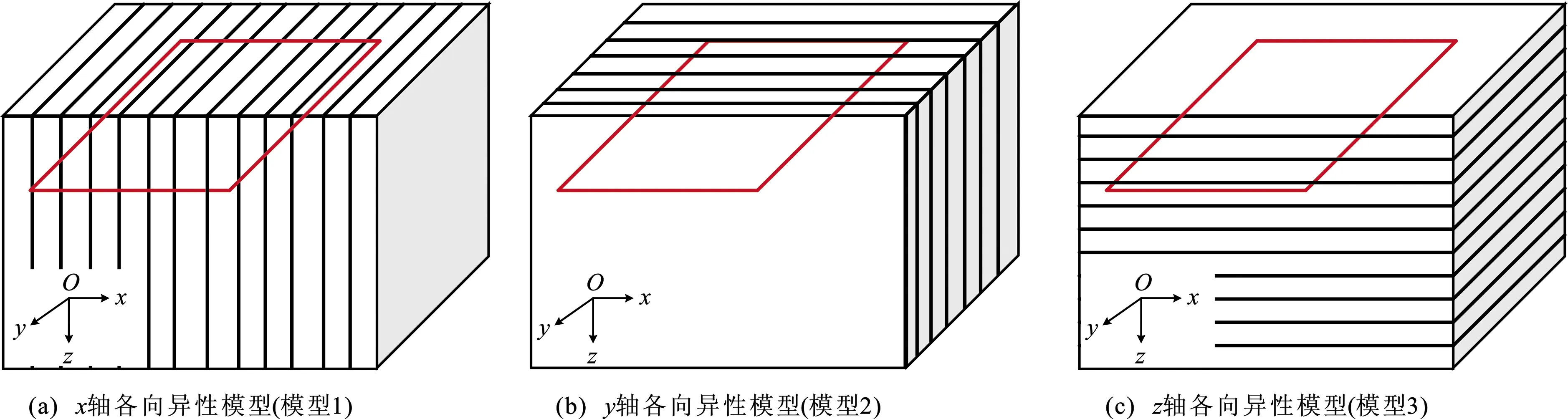
图4 各向异性半空间模型示意图

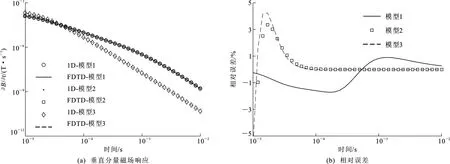
图5 各向异性半空间模型时域有限差分数值解与一维解析解对比

2 数值模拟

2.1 半空间模型地-井瞬变电磁响应

图6 半空间模型示意图

图7为模型a～d的地-井瞬变电磁三分量响应多测道图；图8为半空间模型1 ms时刻三分量响应曲线对比，从左到右依次为∂Bx/∂t、∂By/∂t、∂Bz/∂t分量。由图7可见，模型a～d的∂Bx/∂t、∂By/∂t分量响应多测道图呈反“S”型，∂Bz/∂t分量响应多测道图呈反“C”型。模型a与模型d的三分量响应多测道图形态基本一致，水平分量响应在地下210 m处响应幅值发生正、负变化，在地下500 m处响应幅值趋于0，∂Bz/∂t分量响应极大值在地下60 m处；图8可见1 ms时刻三分量响应幅值一致。模型b的∂Bx/∂t分量响应幅值在地下320 m处发生正、负变化，∂By/∂t分量响应幅值在地下50 m处发生正、负变化；模型c的∂Bx/∂t分量响应幅值在地下50 m处发生正、负变化，∂By/∂t分量响应幅值在地下320 m处发生正、负变化;模型b和模型c的∂Bz/∂t分量响应幅值极大值在地下60 m处；图8可见1 ms时刻三分量响应幅值均大于模型a响应幅值。由于模型在直角坐标系中为轴对称模型，所以模型a的∂Bx/∂t分量与模型d的∂By/∂t分量响应曲线形态一致，模型b的∂Bx/∂t分量与模型c的∂By/∂t分量响应曲线形态一致，模型b的∂By/∂t分量与模型c的∂Bx/∂t分量响应曲线形态一致。由图7、8可见，半空间模型水平轴各向异性特性对地-井瞬变电磁三分量响应的影响大于z轴各向异性。

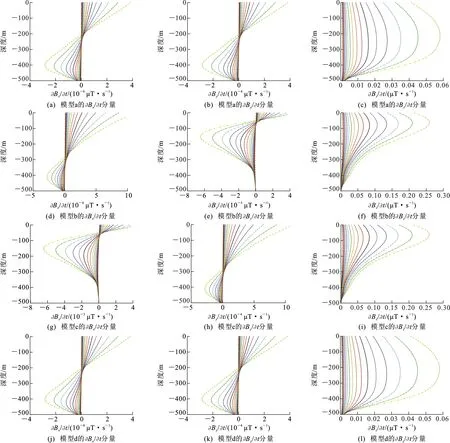
图中不同颜色的线条分别代表不同测道

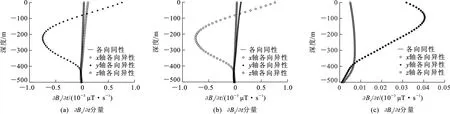
图8 半空间模型1 ms时刻三分量响应曲线对比

2.2 块状异常体地-井瞬变电磁响应

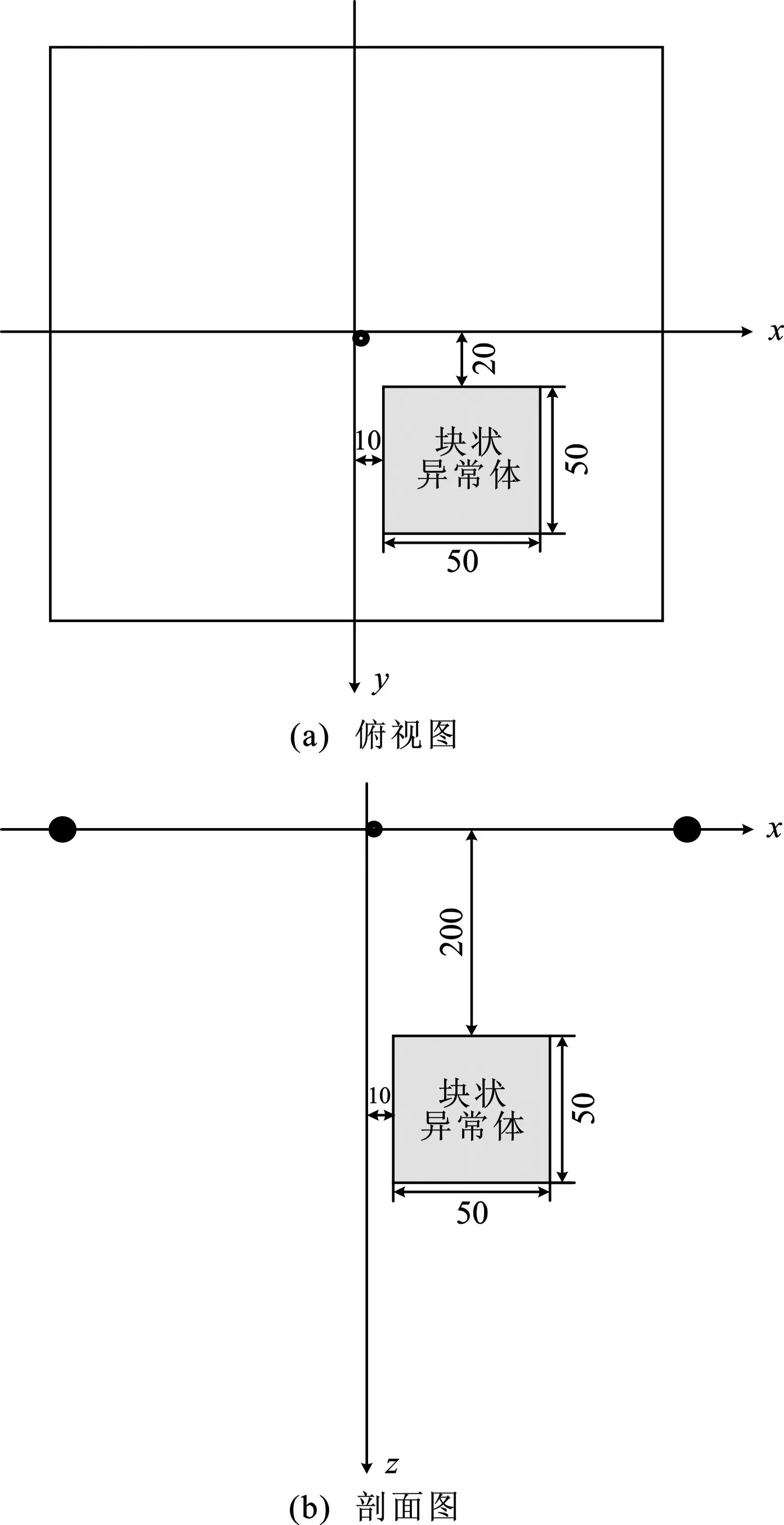
图9 块状异常体模型示意图(单位：m)

图10为块状异常体模型地-井瞬变电磁三分量响应多测道图；图11为块状异常体模型1 ms时刻三分量响应曲线对比，从左到右依次为∂Bx/∂t、∂By/∂t、∂Bz/∂t分量。由图10可见，模型①～④的∂Bx/∂t、∂By/∂t分量响应多测道图整体呈反“S”型，∂Bz/∂t分量响应多测道图呈反“C”型。模型①与模型④的三分量响应多测道图形态基本一致，∂Bx/∂t分量响应在异常体深度位置幅值未变化，∂By/∂t分量响应在异常体深度位置呈“S”型特征，这是由于异常体边界与水平坐标轴距离不一致；模型②和模型③的∂Bx/∂t和∂By/∂t分量响应在异常体深度位置均呈反“S”型特征。模型①～④的∂Bz/∂t分量响应多测道图形态及幅值基本一致。由图11可见：模型④的∂Bx/∂t和∂By/∂t分量响应曲线在异常体深度位置偏离模型①的响应曲线，说明异常体垂直轴各向异性在异常体深度影响异常体地-井瞬变电磁水平分量响应幅值；通过模型②和模型③的∂Bx/∂t和∂By/∂t分量响应发现，x轴各向异性对∂By/∂t分量响应曲线影响大于y轴各向异性，y轴各向异性对∂Bx/∂t分量响应曲线影响大于x轴各向异性，并且异常体与坐标轴的距离变化会影响异常体各向异性对水平分量的影响；模型①～④的∂Bz/∂t分量响应曲线重合，这是由于块状异常体的规模太小以致于电导率各向异性引起的响应曲线变化不足以被发现。

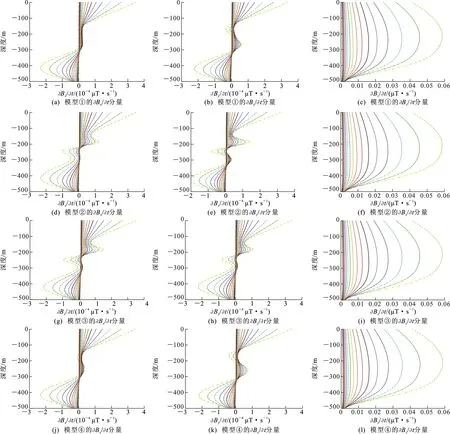
图中不同颜色线条分别代表不同测道

图11 块状异常体模型1 ms三分量响应曲线对比

地-井瞬变电磁三分量数据处理一般采用浮动系数空间交汇算法和最小二乘算法，上述处理方法以异常体产生的纯异常场为基础数据[26-27]。因此，有必要研究异常体的电导率轴向各向异性对地-井瞬变电磁三分量纯异常场响应的影响。以各向同性半空间模型[图6(a)]为背景模型，采用图9所示模型①～④的三分量总场响应分别减去三分量背景响应，得到对应模型的三分量纯异常场。

图12为块状异常体模型的地-井瞬变电磁三分量纯异常场响应多测道图；图13为1 ms时刻的三分量纯异常场响应曲线对比，从左到右依次为∂Bx/∂t、∂By/∂t、∂Bz/∂t分量。由图12、13可见：模型①和模型④的三分量纯异常场响应多测道图形态差别不大，∂Bx/∂t和∂By/∂t分量均呈“S”型特征，∂Bz/∂t分量呈反“C”型特征，并且响应幅值差别不大，只在异常体深度位置出现偏离；异常体x轴和y轴各向异性对三分量纯异常场响应影响较大，模型②和模型③的∂Bx/∂t、∂By/∂t、∂Bz/∂t分量响应多测道图形态相似，∂Bx/∂t、∂By/∂t分量整体呈“S”型特征，在异常体深度位置出现反“S”型特征，∂Bz/∂t分量整体呈反“C”型特征，在异常体深度位置出现局部的“C”型特征。通过模型②和模型③的∂Bx/∂t、∂By/∂t分量纯异常场响应，发现y轴各向异性大于x轴各向异性对∂Bx/∂t分量纯异常场响应的影响，y轴各向异性小于x轴各向异性对∂By/∂t分量纯异常场响应的影响，并且异常体与坐标轴的距离变化会影响异常体各向异性对水平分量纯异常场的影响。

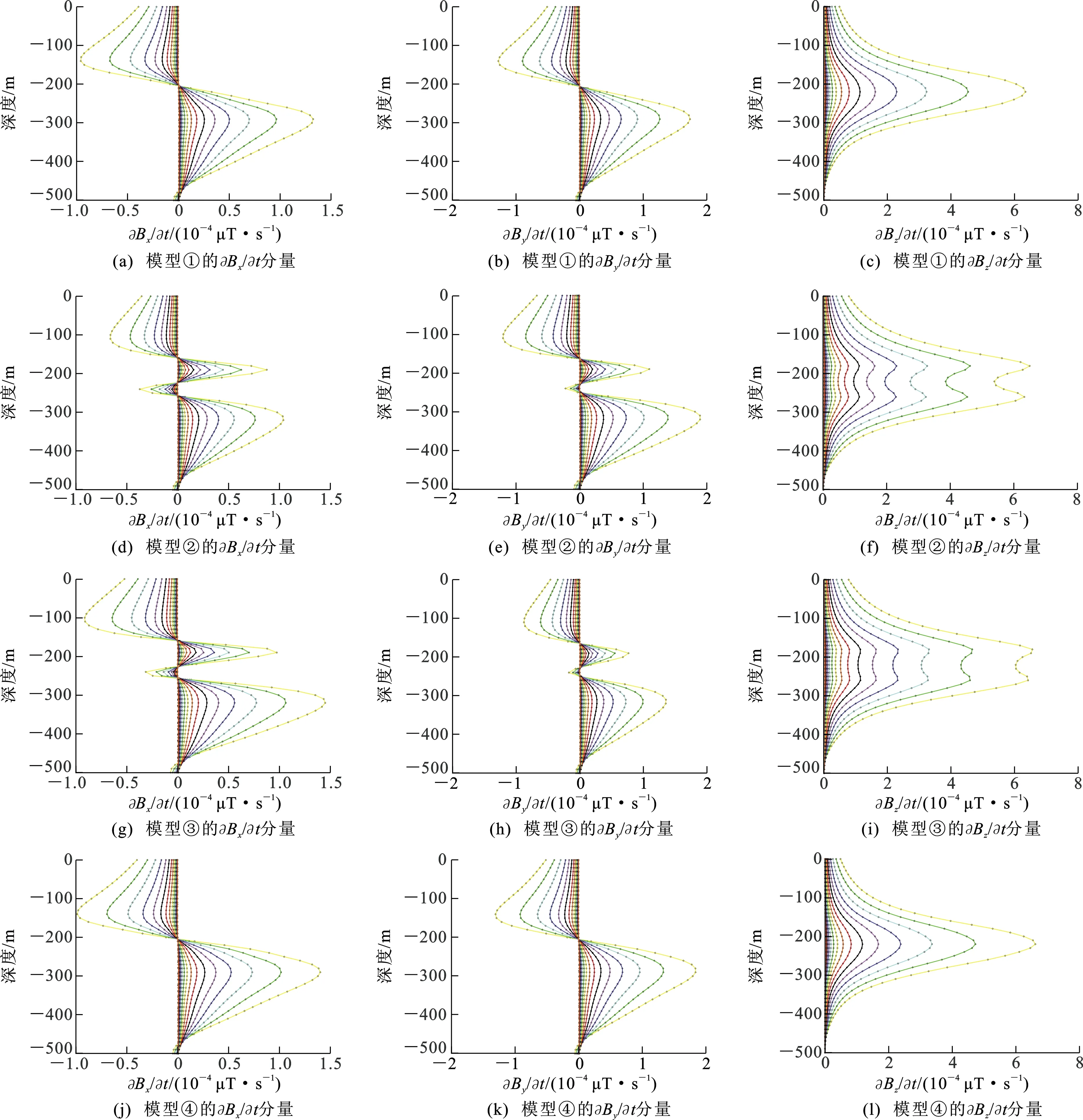
图中不同颜色线条分别代表不同测道

图13 块状异常体模型1 ms时刻三分量纯异常场响应曲线对比

3 结 语

(1)通过半空间模型发现水平轴各向异性对地-井瞬变电磁三分量响应大于垂直轴各向异性；通过块状异常体模型发现x轴各向异性对∂By/∂t分量响应影响大于y轴各向异性，y轴各向异性对∂Bx/∂t分量响应影响大于x轴各向异性。

(2)地层电导率轴向各向异性对地-井瞬变电磁三分量响应具有较大影响，为提高地-井瞬变电磁法的精细精度，需要进一步研究不同地电类型、不同各向异性异常体方位等参数对地-井瞬变电磁三分量响应的影响特征，为精细探测提供指导依据。