电性源短偏移距瞬变电磁场扩散规律三维数值模拟

常江浩，薛国强

(1.中国科学院地质与地球物理研究所 中国科学院矿产资源研究重点实验室，北京 100029；2.中国科学院大学 地球与行星科学学院，北京 100049；3.中国科学院地球科学研究院，北京 100029；4.河北地质大学 河北省战略性关键矿产资源重点实验室，河北 石家庄 050031；5.长安大学 地球物理场多参数综合模拟实验室(中国地球物理学会重点实验室),陕西 西安 710054)

0 引 言

随着经济的快速发展，中国对矿产资源的需求量逐渐增大。中国成矿地质条件良好，资源潜力巨大，但目前矿产勘探开采深度大多小于500 m，受到勘查技术和装备方面的限制，深部矿产资源无法被有效识别。因此，加强对深部资源的探测，提高危机矿山的深部和外围找矿能力，发现接替资源，是勘探工作的重中之重[1-2]。瞬变电磁法是一种建立在电磁感应原理基础上的时间域电磁探测方法，具有勘探深度大、不受高阻层屏蔽、工作效率高等优点，在深部矿产资源勘探中发挥着重要作用[3-7]。

瞬变电磁法按照发射源形式可分为回线源瞬变电磁法和电性源瞬变电磁法。回线源装置不受接地条件限制，对低阻体分辨能力高，在金属矿勘探、煤矿水害探查和工程勘察等领域有着广泛的应用[8-12]。但回线源对高阻体分辨能力较差，其场能量在地层中衰减较快，一般只能达到几百米的探测深度。电性源采用接地导线源发射电磁场，其产生的电场不仅具有水平分量，还具有垂直分量，电场水平分量有利于低阻体的探测，垂直分量有利于高阻体的探测[13]。传统的电性源装置形式为长偏移距装置，长偏移距接收信号强度随收发距增大将急剧减小，信噪比下降，不利于精细探测。薛国强等针对近源探测的优越性，对电性源短偏移距瞬变电磁(SOTEM)响应进行了研究，并提出了电性源短偏移距瞬变电磁法[14-15]。理论和实践表明，电性源短偏移距瞬变电磁法采用的近源探测形式不仅有较高的信噪比，还能达到较大的探测深度[16-18]。

崔江伟对电性源短偏移距瞬变电磁全程视电阻率求取方法进行了研究，并分析了全程视电阻率对薄层的分辨能力[19]。陈卫营等对电性源短偏移距瞬变电磁各分量响应衰减特征进行了分析，并基于一维模型对电场和磁场的敏感区域进行了研究[20]；之后，又建立了电性源短偏移距瞬变电磁数据的一维OCCAM反演方法，并将其应用于三维电性源短偏移距瞬变电磁数据的反演[21]。陈康对电性源短偏移距瞬变电磁多分量响应特征进行了研究，并对各个分量的探测能力进行了分析[22]。目前对电性源短偏移距瞬变电磁响应特征的研究主要基于一维模型，且主要讨论电场Ex分量和磁场Hz分量的响应特征和探测能力，不利于复杂目标体的精细探查。

本文基于三维时域有限差分法，研究了电性源短偏移距瞬变电磁场在层状地层中的扩散规律，并采用三维异常体模型研究了三维异常体对电性源短偏移距瞬变电磁场的影响，以期推进电性源短偏移距瞬变电磁法的基础理论研究。

1 原 理

1.1 差分方程

时域有限差分法是瞬变电磁场三维数值模拟的主要方法，其采用的网格单元如图1所示[23]，这样的网格形式使三维体表面上场分量的连续性条件自然得到了满足。在无源区域，麦克斯韦(Maxwell)方程组的微分形式[23]为

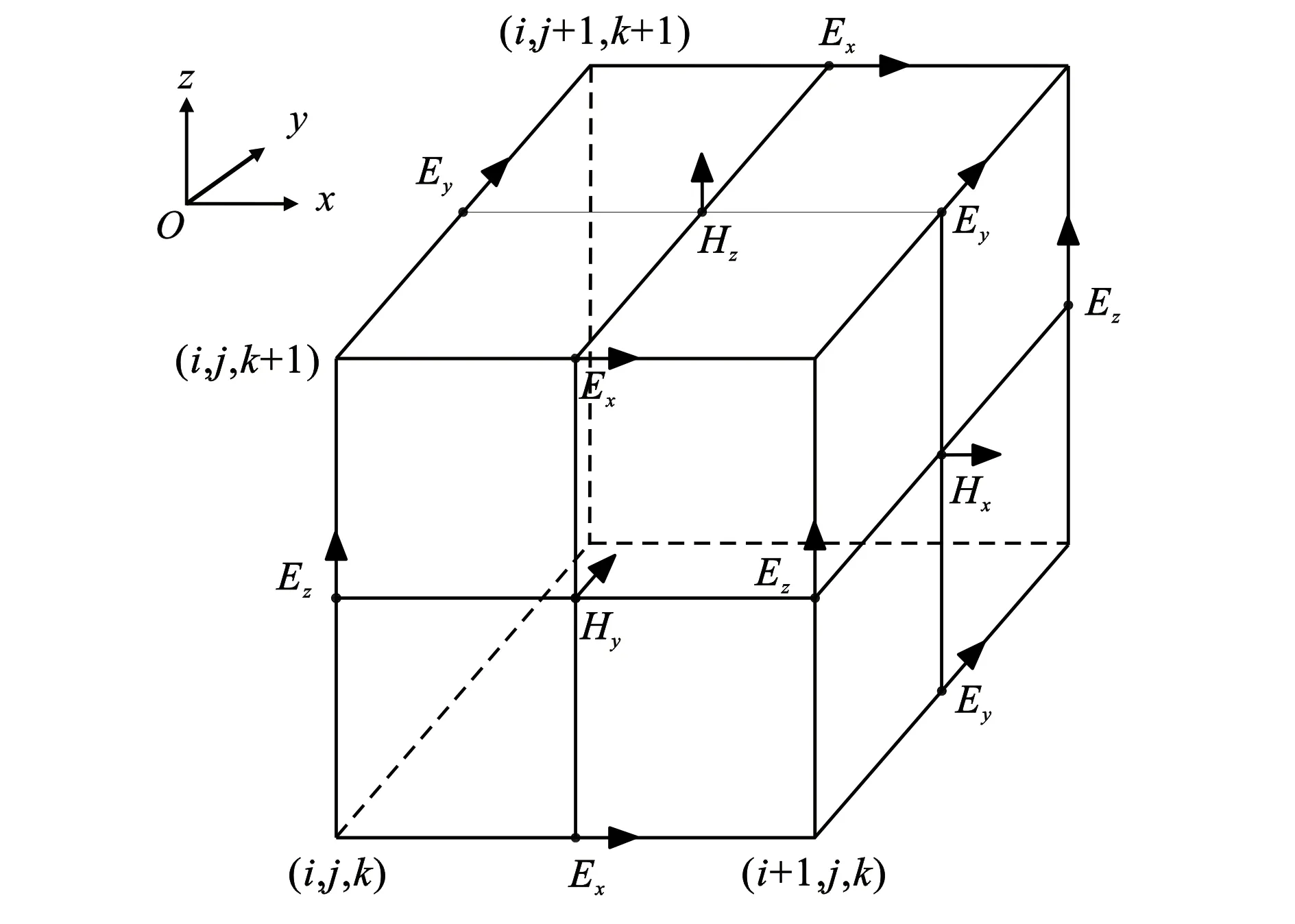
i、j、k分别为x、y、z方向网格剖分的节点；Ex、Ey、Ez分别为x、y、z方向上的电场分量；Hx、Hy、Hz分别为x、y、z方向上的磁场分量；图件引自文献[23]

(1)

(2)

(3)

(4)

式中：E为电场强度；B为磁感应强度；H为磁场强度；σ为介质电导率；ε为介电常数；t为时间；D为位移电流。

受稳定性条件限制，空气中电磁场的有限差分迭代需要采用较小的时间步长影响计算效率。根据时间域电磁场的传播特点，在一次场关断后的初期，地面波以光速从空气中传播到地表各点，此时的场主要以地面波为主，随着时间的推移，以地面波传播的场逐渐衰减，至晚期以地面波传播的场可忽略不计，晚期的场主要来自地层波。本文根据场在早期和晚期的特征分别采用了不同的有限差分算法，早期直接采用动态电磁场方程计算以保证地面波的精度，而晚期采用准静态电磁场方程计算以提高计算效率。

在准静态近似下，式(2)可忽略位移电流项。为了满足显式时间步进格式，Wang等引入了虚拟位移电流项[24]，其表达式为

(5)

虚拟介电常数的引入使计算晚期场时可以放宽对时间步长的要求[24]。将式(5)进行差分离散即可得到无源区域准静态近似下电场的差分方程，具体离散过程可参考文献[24]。

1.2 接地导线源的加载及边界条件

瞬变电磁场直接时域数值模拟中，发射源的加载方式主要有3种：①利用负阶跃电流在均匀半空间产生的解析解作为场的初始值；②将源电流密度加入麦克斯韦方程，一般采用梯形电流波形；③取关断前建立的稳定场作为场的初始值。第①种方法要求发射源附近为均匀介质，一般用来计算磁偶极子源产生的初始场；第②种方法对模型没有限制，可以模拟任意波形发射电流的瞬变电磁响应；第③种方法需要求解稳定电流场，为了避免求解磁场初始值，在迭代中一般用磁场的时间导数代替磁场。本文采用第②种方法加载发射源，该方法对模型没有限制，可以模拟任意发射电流激发的瞬变电磁响应。

在有源区域，式(2)可修改[25]为

(6)

式中：Js为源电流密度。

在施加接地导线源时，可将导线源与电场分量的空间位置重合。将式(6)进行差分离散即可得到有源区域准静态近似下电场的差分方程，具体离散过程可参考文献[25]。

边界条件是影响晚期场精度的主要因素，有效吸收边界不仅能提高解的精度，而且能减少网格数量。本文在截断边界采用卷积完全匹配层(CPML)吸收边界条件[26-27]。卷积完全匹配层吸收边界不仅具有完全匹配层(PML)的性能，还能对低频场进行有效吸收[28]。

1.3 算法验证

采用均匀半空间模型对算法的精度进行验证，地下介质电阻率为100 Ω·m，空气电阻率为1.0×105Ω·m，在地表布设长度为100 m的电性源，在偏移距800 m处接收。发射电流波形为梯形波，梯形波宽度为100 ms，上升沿和下降沿宽度为10 μs。验证结果如图2所示，将时域有限差分解与解析解进行对比。从电场衰减曲线[图2(a)]可以看出，时域有限差分解与解析解在各个时段都非常吻合；从相对误差曲线[图2(b)]可以看出，最大相对误差小于5%。这说明本文采用的有限差分法具有较高的精度。

图2 时域有限差分解与解析解对比

2 电性源短偏移距瞬变电磁场扩散规律

电性源短偏移距瞬变电磁法采用近源观测方式，近源处瞬变电磁场的扩散规律与大偏移距处不同，研究电性源短偏移距瞬变电磁场的扩散规律对于认识近源处瞬变电磁场与地质体的相互作用过程以及最佳观测场量的选择具有重要作用。本文采用如图3所示的层状地层模型，地下地层被分为3层。第一层和第三层电阻率为100 Ω·m，第二层电阻率为10 Ω·m(低阻层)或1 000 Ω·m(高阻层)，分别代表H型地层模型和K型地层模型。其发射源长度为200 m，沿x轴方向布设，中点位于坐标原点，发射电流为1 A。

h1、h2、h3分别为第一、二、三层地层的厚度

采用三维时域有限差分法进行正演模拟计算，图4～6分别为电场各分量在y=200 m剖面上的等值线分布。从图4可以看出，电场Ex分量下部出现负值区域，为返回电流影响。在1 ms时，电场Ex分量上部正极值区域主要集中在发射源附近，随着时间的推移逐渐向下扩散；在10 ms时，H型地层模型的电场Ex分量极值区域位于低阻层附近，而K型地层模型的电场Ex分量极值区域已经穿过高阻层，说明电场在低阻层中扩散速度较慢，在高阻层中扩散速度较快。从图5可以看出，电场Ey分量正极值区域和负极值区域分别位于发射源两端，并随着时间的推移逐渐向下、向外扩散。从图6可以看出，电场Ez分量在地层分界面急剧变化，这主要受地层界面处存在的面电荷影响。对于H型地层模型，低阻层内部电场Ez分量幅值小于上方和下方地层，而K型地层模型的高阻层内部电场Ez分量幅值大于上方和下方地层。以上电场的三维模拟结果与陈卫营等的一维模拟结果[29]基本吻合，进一步说明了本文采用的三维模拟方法的可靠性。

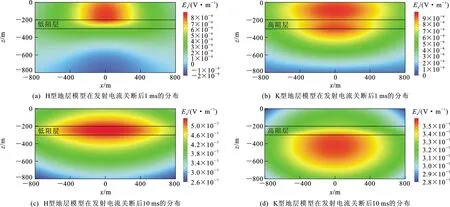
图4 不同时刻电场Ex分量等值线分布

图5 不同时刻电场Ey分量等值线分布

图6 不同时刻电场Ez分量等值线分布

图7～9为磁场各分量在y=200 m剖面上的等值线分布。从图7可以看出，磁场Hx分量正极值区域和负极值区域分别位于发射源两端，并随着时间的推移逐渐向下、向外扩散。从图8可以看出，磁场Hy分量上部为负值区域，下部为正值区域，说明磁场Hy分量也会受到返回电流影响。比较H型和K型地层模型的结果，磁场Hy分量在低阻层中扩散较慢，在高阻层中扩散较快，且低阻层对磁场Hy分量扩散影响较大。图9为磁场Hz分量的等值线分布，磁场Hz分量极值区域主要位于发射源下方，并随着时间的推移逐渐向下移动。受中间异常层的影响，在10 ms时，H型地层模型的磁场Hz分量极值区域位于低阻层附近，而K型地层模型的磁场Hz分量极值区域已经穿过高阻层，说明低阻层扩散速度较慢，高阻层扩散速度较快。整体上，低阻层对磁场Hz分量扩散影响较大，高阻层对磁场Hz分量扩散影响较小。

图7 不同时刻磁场Hx分量等值线分布

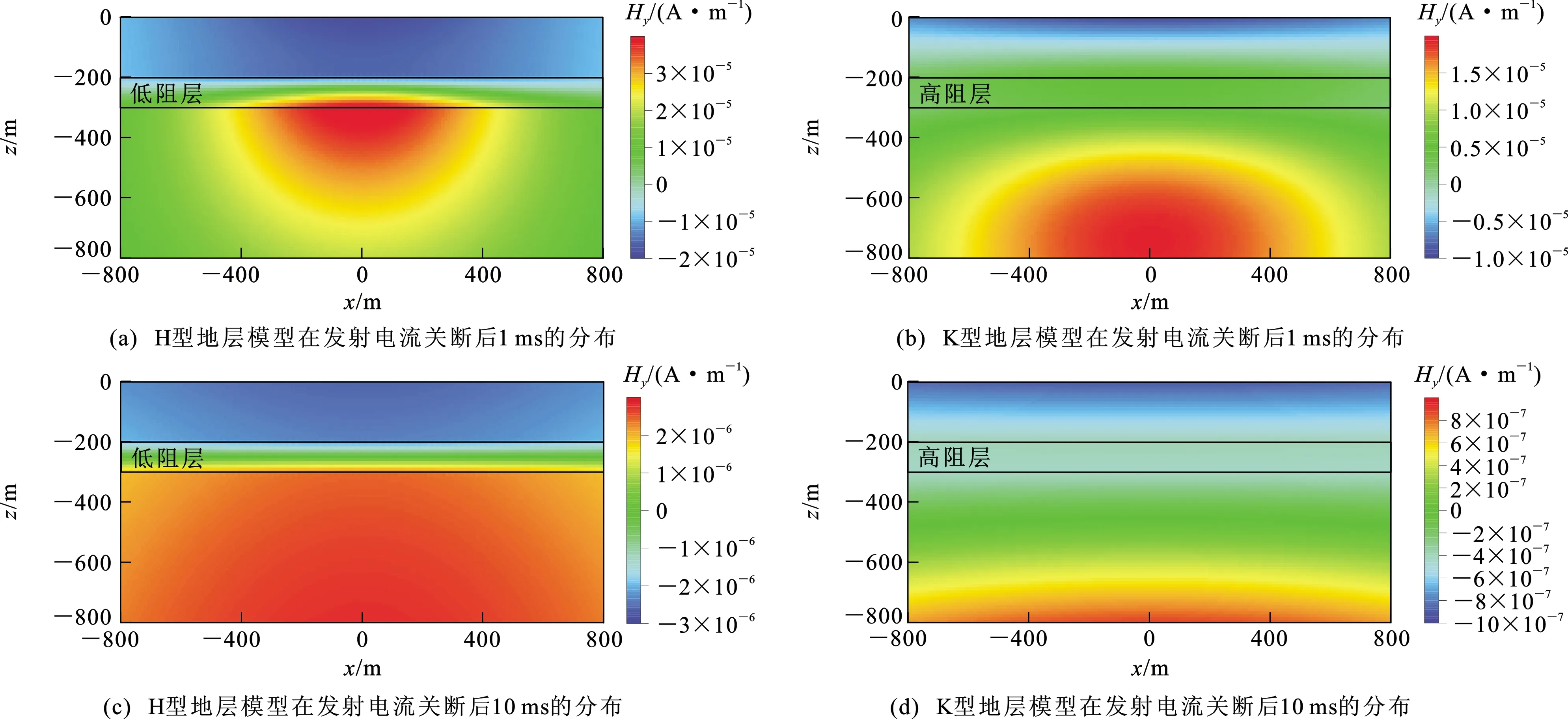
图8 不同时刻磁场Hy分量等值线分布

图9 不同时刻磁场Hz分量等值线分布

3 三维异常体影响下电性源短偏移距瞬变电磁场平面分布特征

为认识三维异常体影响下电性源短偏移距瞬变电磁场的扩散规律，建立了如图10所示的含三维异常体的地电模型。均匀半空间含有一低阻异常体，大小为200 m×200 m×200 m，埋深为100 m。发射源长度为200 m，沿x轴方向布设，中点位于坐标原点，发射电流为1 A。异常体位于发射源赤道位置，距离发射源400 m。均匀大地电阻率设为100 Ω·m，异常体电阻率为10 Ω·m。

图(b)括号中的数据为电阻率

采用三维时域有限差分法进行正演模拟计算，图11、12为发射电流关断后不同时刻在地表观测到的电场Ex、Ey分量的等值线分布(在地表无法观测电场Ez分量)。从图11可以看出：在1 ms时，电场Ex分量在异常体位置发射畸变，等值线凹向发射源方向，说明低阻异常体使电场扩散速度减慢；在10 ms时，Ex分量在异常体上方出现极小值，在异常体两侧出现极大值。从图12可以看出，电场Ey分量显示出了4个异常区域，均位于异常体外部且分布在异常体四周。

图11 异常体影响下电场Ex分量平面分布

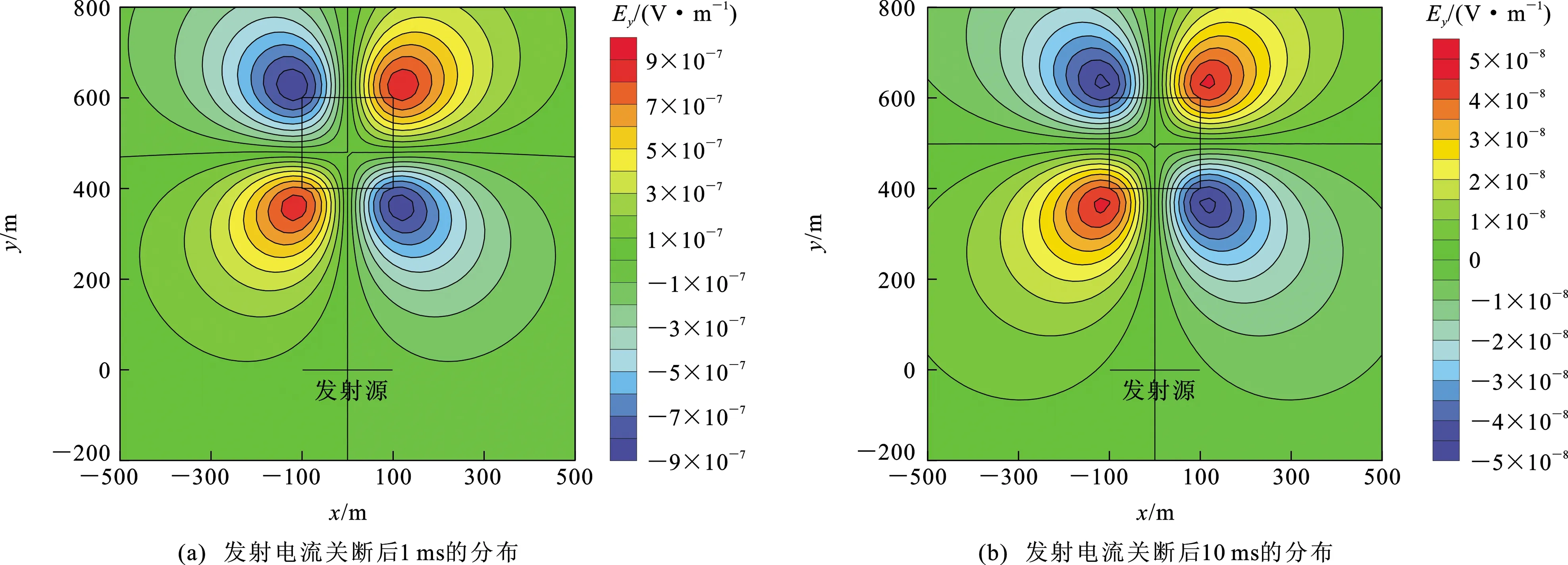
图12 异常体影响下电场Ey分量平面分布

图13～15为发射电流关断后不同时刻在地表观测到的磁场各分量的等值线分布。从图13可以看出，由于受到异常体的吸引，磁场Hx分量在异常体外部产生畸变。从图14可以看出：在1 ms时，磁场Hy分量的分布受异常体影响较小，随着时间的推移，其分布受异常体影响逐渐增大；在10 ms时，其等值线出现两个极小值区域，一个位于发射源附近，另一个位于异常体上方，说明低阻异常体会使磁场Hy分量产生负异常。图15为磁场Hz分量的等值线分布，其等值线在异常体两侧(靠近发射源和远离发射源位置)畸变较大，而在异常体上方没有明显异常。

图13 异常体影响下磁场Hx分量平面分布

图14 异常体影响下磁场Hy分量平面分布

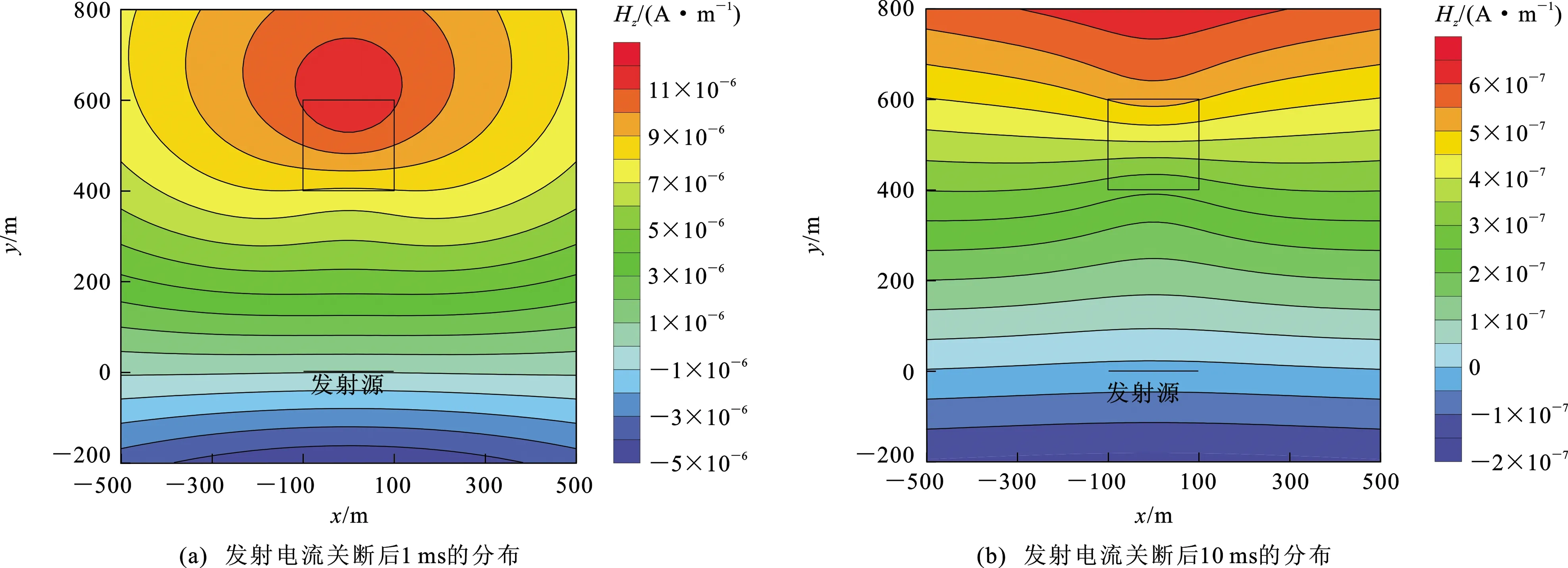
图15 异常体影响下磁场Hz分量平面分布

以上分析表明，电性源短偏移距瞬变电磁场的5个分量对异常体的灵敏区域不同。电场Ex分量和磁场Hy分量在异常体上方异常最大；而电场Ey分量和磁场Hx分量异常响应最大值位于异常体外部，且分布在异常体四周；磁场Hz分量在异常体两侧(靠近发射源和远离发射源位置)异常最大。这说明电性源短偏移距瞬变电磁场的5个分量在地表应选择不同的区域进行观测。

4 结 语

(1)电场Ex分量的正极值区域主要集中在发射源附近，并随着时间的推移逐渐向下扩散；电场Ey分量正极值区域和负极值区域分别位于发射源两端，并随着时间的推移逐渐向下、向外扩散；电场Ez分量在地层分界面产生跃变，说明在地层分界面处存在面电荷。

(2)磁场Hx分量正极值区域和负极值区域分别位于发射源两端，并随着时间的推移逐渐向下、向外扩散；磁场Hy分量上部为负值区域，下部为正值区域，说明磁场Hy分量也会受到返回电流影响；磁场Hz分量极值区域主要位于发射源下方，并随着时间的推移逐渐向下移动。

(3)对于三维异常体，电场Ex分量和磁场Hy分量的灵敏区域位于异常体上方；而电场Ey分量和磁场Hx分量的灵敏区域位于异常体外部，且分布在异常体四周；磁场Hz分量的灵敏区域位于异常体两侧(靠近发射源和远离发射源位置)。这说明电性源短偏移距瞬变电磁场的5个分量对三维异常体的灵敏区域不同，不同的分量应选择不同的区域进行观测。