基于PRM优化算法的移动机器人路径规划

程 谦 高 嵩 曹 凯 陈超波

(西安工业大学电子信息工程学院 陕西 西安 710021)

0 引 言

近些年移动机器人技术得到了飞跃性的进步，而路径规划作为移动机器人技术的重要基础成为了研究的热点。目前，路径规划算法被应用于工业、服务、娱乐等各个方面，例如无人车、扫地机器人、餐厅机器人等。机器人在执行任务时都依赖路径规划算法，而有效的路径规划技术可以使机器人完成任务时节省大量的物力财力，同时也可以提高执行任务时的安全性[1]。

根据路径规划在规划过程中搜索的方式不同主要分为三大类：基于图论的路径搜索算法，基于离散采样的规划算法，智能路径规划算法。基于图论的搜索算法于1959年被提出，主要思想是将状态空间定义为占据网格，将障碍定义为不可访问的网格点，然后算法搜索可用的网格点，如果路径存在，则给出解决方案。如果网格分辨率足够，基于图论的算法可以保证解决方案。Dijkstra算法[2]作为图论经典的算法被广泛应用，随后又发展出A*算法[3]、DFS算法[4]等。文献[5]将图论的规划方法与其他算法进行了比较，在解决两点之间最短距离的情况下，图论的方法较其他算法有较大的优势。基于离散采样的规划算法的主要思想是在配置空间中选择非结构有限数量的点，并在这些点之间建立连接。基于采样的方法是简单、通用、高效和概率完备的(当时间接近无限时一定有解)，如随机路径图法(PRM)[6]、快速随机扩展树(RRT)[7]等。基于采样的规划算法虽然一定能够规划出路径，但是因为其离散随机的特性解不一定是最优的。以PRM算法为例，在面对含有狭窄通道时算法的效率和成功率会明显下降。针对这个问题文献[8]提出了一种长短期存储器(LSTM)模型，通过预测障碍物位置，将障碍物轨迹划分为时间序列，并将下一时刻的位置估计引入到规划算法的状态有效性测试中，以生成最优路径。通过对障碍物模型的预测，可以减少穿越和重编程的时间，通过优化采样阶段，也可以增加狭窄通道中采样点的数量，从而提高算法的效率。智能路径规划算法是近些年慢慢发展起来的一个热门方向，因为人工智能的兴起，越来越多的智能算法被应用在移动机器人路径规划上，如遗传算法[9]、粒子群优化算法[10]、蚁群算法[11]和人工势场法[12]等。文献[13]将人工势场法和遗传算法进行结合，通过引入指数因子来模拟斥力，从而解决了机器人在寻找路径过程中易陷入局部极小值的问题，然后利用遗传算法进行寻优，找出最优路径。

目前，随着机器人应用范围越来越广，机器人所处环境的障碍物也越来越复杂。基于图论搜索的传统规划算法需要精确定位障碍物，其算法计算量过大，在现实中非常不适用。而基于离散采样规划算法的PRM算法可以有效避免对位姿空间精确定位，并且算法的复杂度并不依赖于地图的复杂度，所以可以有效地应用于实际。但是PRM算法在实际的应用中也会有各种问题，例如在处理狭窄通道方面有明显的不足。针对这个问题，文献[14-16]提出了利用高斯采样、桥测试法和自适应采样研究方法，旨在提高狭窄通道中的采样点个数，从而提高对狭窄通道的适应性。此外，PRM算法因为采样点个数较多，所花费的时间较长，大大限制了其应用性。文献[17]提出了减少碰撞检测的思想来加大算法的效率，但是在一定程度上又增加了算法复杂性。

本文对PRM算法进行深入研究，提出一种基于连接点的优化方法，剔除算法在学习阶段构建的无效路径，使路径总数减少，从而缩短在查询阶段的搜索时间，有效地提高了PRM算法的规划速度。同时因为规划出的路径连接了更多的采样点，使路线在弯道有更好的适应性，显著提升了路线的安全性。

1 PRM算法基本原理

通过在环境中建立路径网络图，将连续的空间转化为离散的空间，然后再进行路径规划，使算法的复杂程度只依赖于搜索路径的复杂度，从而使复杂程度降低。PRM算法也可以用在多自由度的移动机器人路径规划中，而且可以有效地克服局部极小值的缺点，在解决高维空间和复杂障碍物的情况下有计算量小的优势。

PRM算法的基本思想是用概率图来表示移动机器人所处环境的自由空间。在自由空间内进行随机采样，把采样点加入到图集中，利用局部规划器把各个采样点进行连接，构成路径网络图，然后在这个随机网络中使用搜索算法来找到移动机器人的可行路径。该算法可以分两个阶段完成，即离线学习阶段和查询阶段。

1.1 学习阶段

在自由空间中进行尽可能随机且均匀的采样，然后连接各个点，构建出一幅路径网络图。

学习阶段具体步骤如下：

1)创建采样点集x

2)在地图中采用均匀采样随机采取一点ni

3)while:采集到足够的采样点跳出

4) if:ni在障碍物内

5)舍弃该点

6)else:将ni加入到点集x

7)end

8)创建路径集f

9)while:分别依次连接点集x中的两点xinit,xgoal

10)if:两点之间连线碰撞到障碍物

11)舍弃该路线

12)else:将两点之间路线加入路径集f

13)end

14)建立无向网络图G(x,f)

15)if:G(x,f)为空

16)不存在路径

17)else:查找最优路径

PRM算法学习阶段是在地图内进行随机采样，并对采样点进行碰撞检测，从而保证采样点不会落在地图障碍物内，使采样点随机均匀地分布在自由无障碍空间内。采样完成后通过连接各个点，构建路径网络图。构建网络图时，采用从一个点开始，向周围点扩散的方法，如果两个点之间可以连接，并且没有碰到障碍物，就把路线添加到网络图中，反之则舍弃，从而构建出整幅路径网络图，如图1所示。其中：左上角大圆点代表起始点；右下角大圆点代表终点；黑色为障碍物；小点为采样点；细线为路径网络图中路径。

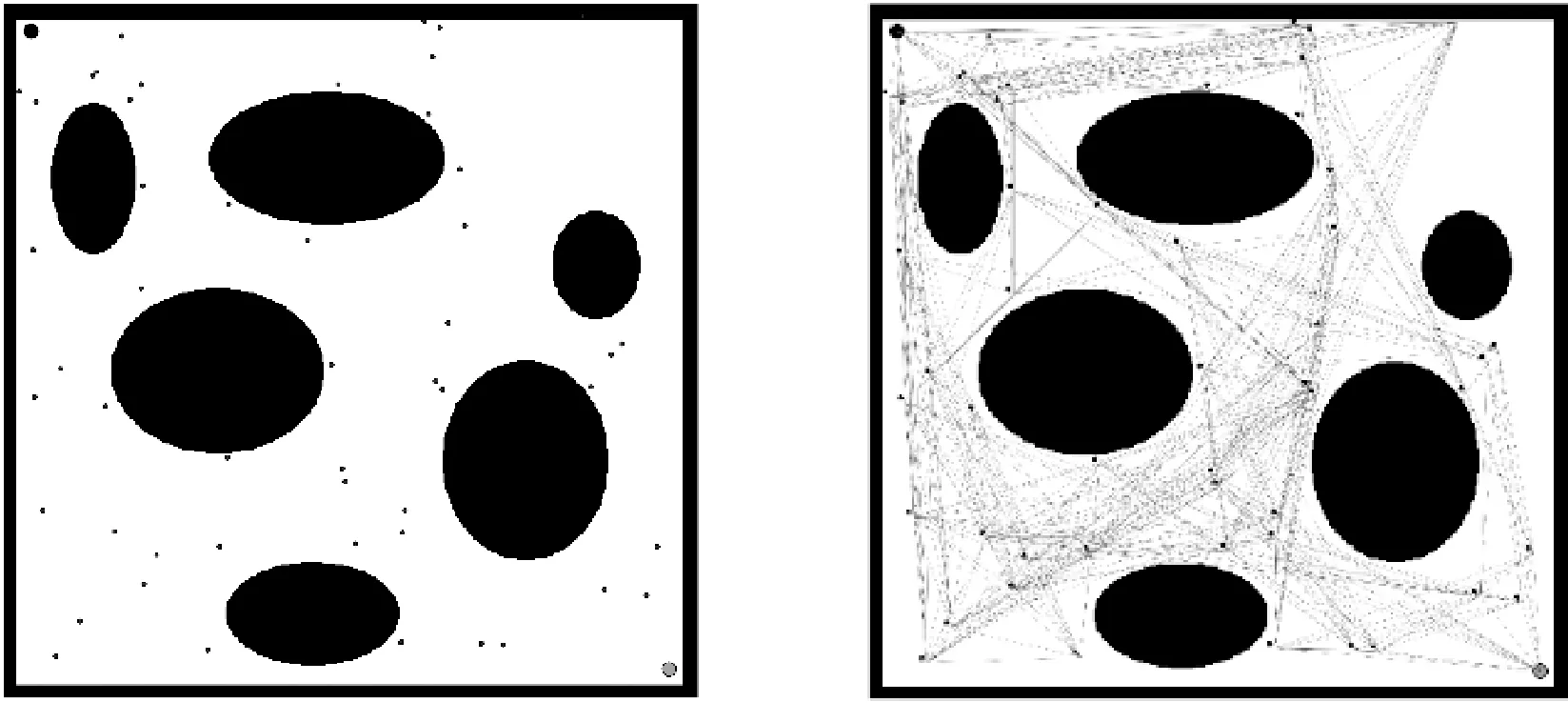
(a)采样图 (b)网络路径图

1.2 查询阶段

查询阶段步骤利用学习阶段建立好的无向路径网络图，在无向网络图中设置好起点和终点，根据设置好的起点和终点搜索出一条符合需求的路径，具体可以分为以下三步：

(1)把地图中离起始点和目标点最近的两个点分别进行连接；

(2)在网络图中搜索路径，找到起始点到目标点的路线；

(3)找到路径后，通过平滑处理，优化路径。

最终结果如图2所示，深色粗线为规划出的路线。

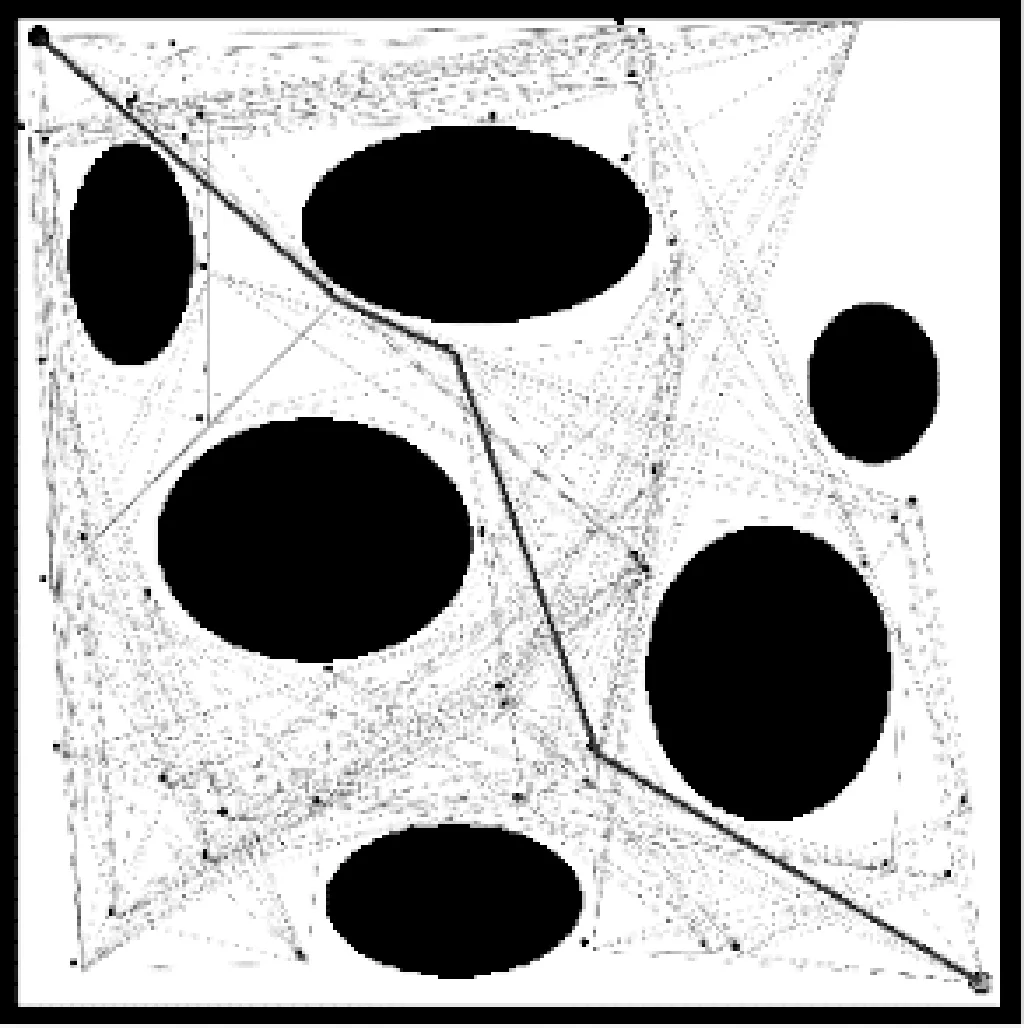
图2 PRM查询阶段

2 PRM算法优化

PRM算法在学习阶段通过对随机地图进行均匀采样，使采样点在障碍物地图中均匀分布，通过连接各个采样点构建出路径网络图，随后在查询阶段中利用A*算法进行路径查询，从而寻找出最优路径。在PRM算法整个阶段中学习阶段花费的时间最少，影响算法整体效率的主要是查询阶段，而路径网络图中的路径数量直接影响查询阶段花费的时间。

为了有效地减少路径网络图中的路径数量，对学习阶段进行改进。通过改变连接点的距离，使一些连接距离较远且不合理的路径大大减少，导致算法在查询阶段查找的路径减少，从而减少花费的时间，进而提高运算效率。以未优化前一个点所构成的路径网络图为例，如图3(a)所示，A点在学习阶段连接各个点，构建一幅不接触障碍物的路径网络图(如果路线接触障碍物自动舍弃不连接)。为了减少路径的数量，限定采样点的连接距离，经过优化后A点的连接如图3(b)中实线所示，距离A点较远的E点和F点不进行连接，使构成的路径网络的路径数量大大减少。

因为限定了连接点的距离，优化后的路线图中路线较长的路径消失，为了寻找到最优路径，路线图会连接更多的采样点，使得规划出的路径在弯道处更加灵活，加大路线离障碍物的距离，如优化前A-F和A-E路线(图3(a)中所示)优化后变为A-H-F和A-C-D-E路线(图3(b)中虚线所示)。虽然优化后的路线在一定程度上加大了最终规划出来路径的长度，但是使得路线更加安全可靠，加大了在实际中的应用性和实用性。

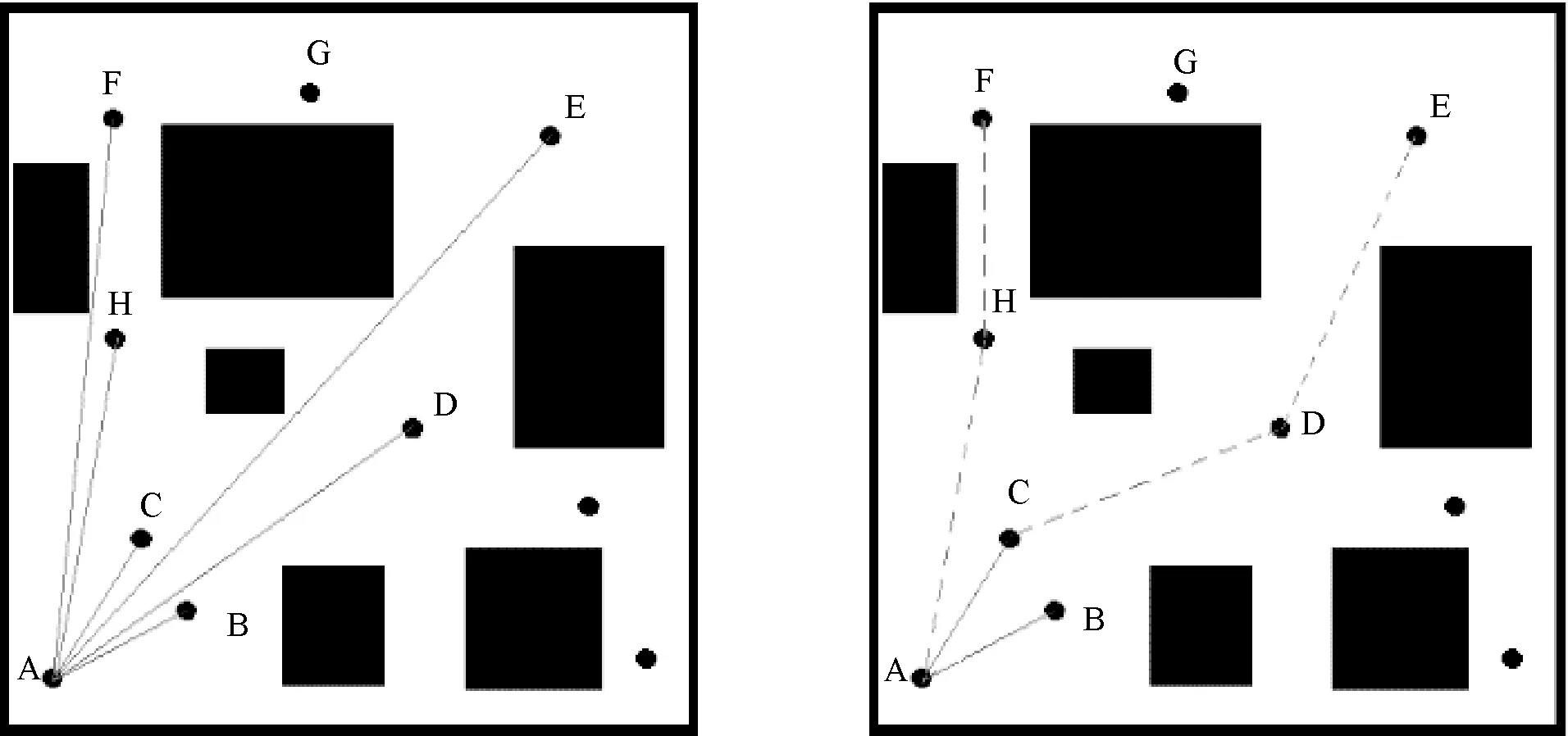
(a)优化前 (b)优化后

优化过程中连接点限定距离的取值可以根据实际地图情况进行选取。限定距离取值越大越接近传统PRM算法，优化效果越弱；限定距离越小，网络路径图中路线的数量越少，并且构成最优路径时连接的采样点越多，效果越显著。但当限定距离过小时，因为连接不到采样点，可能使路径规划失败，所以设置最小值，在最小值上依次叠加，直到取到第一个采样点，进而找到能保证规划成功的最小限定距离。

3 优化算法仿真及结果分析

为了验证改进算法的有效性，在如图4所示的两种地图中进行仿真，同时与优化前PRM算法进行对比。在仿真过程中为计算方便，设置连接点最小距离为1米，仿真实验的采样点数量为150和300，对比在不同采样点情况下优化算法的优化效果。

(a)简单障碍物地图 (b)复杂障碍物地图

3.1 算法仿真

当采样点N=50时，简单地图优化前后结果如图5(a)和图5(b)所示，能够规划出路径，并且经优化后路径网络图中的路径数量明显减少，并且路线较传统相比离障碍物较远。复杂障碍物地图优化前后如图5(c)和图5(d)所示，因为采样点过少，在建立出的路径网络图中没有可以到达目标点的路径，规划失败。

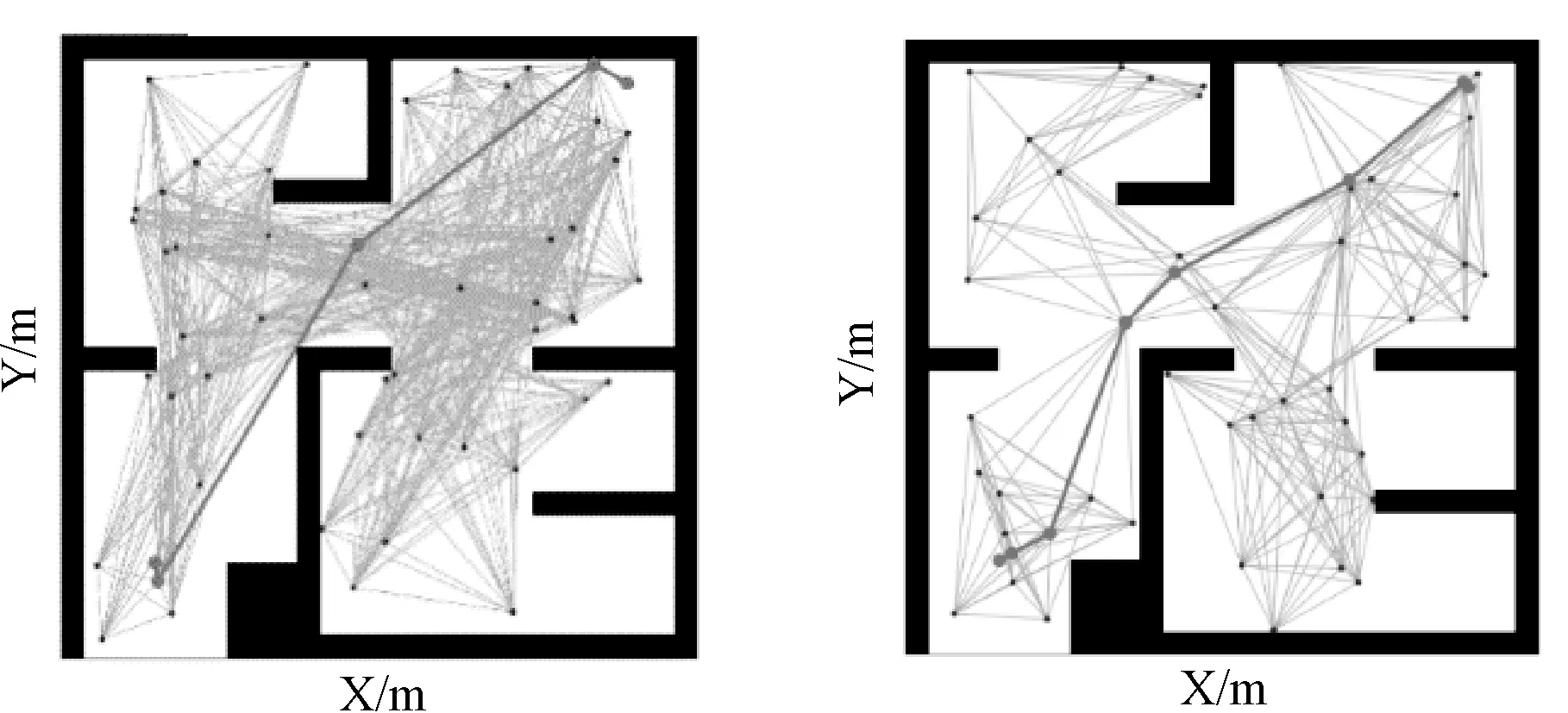
(a)简单障碍物地图优化前 (b)简单障碍物地图优化后

当采样点N=150时，简单地图优化前后结果如图6(a)和图6(b)所示，优化前所构成的路径网络图都有较多的路径，优化后路径显著减少，都能够合理地规划出路径，但优化后的路径在弯道处离障碍物较远，安全性比优化前增强。复杂地图优化前后结果如图6(c)和图6(d)所示，优化后路径网络图中路径的数量明显减少，并且路径安全显著增强。

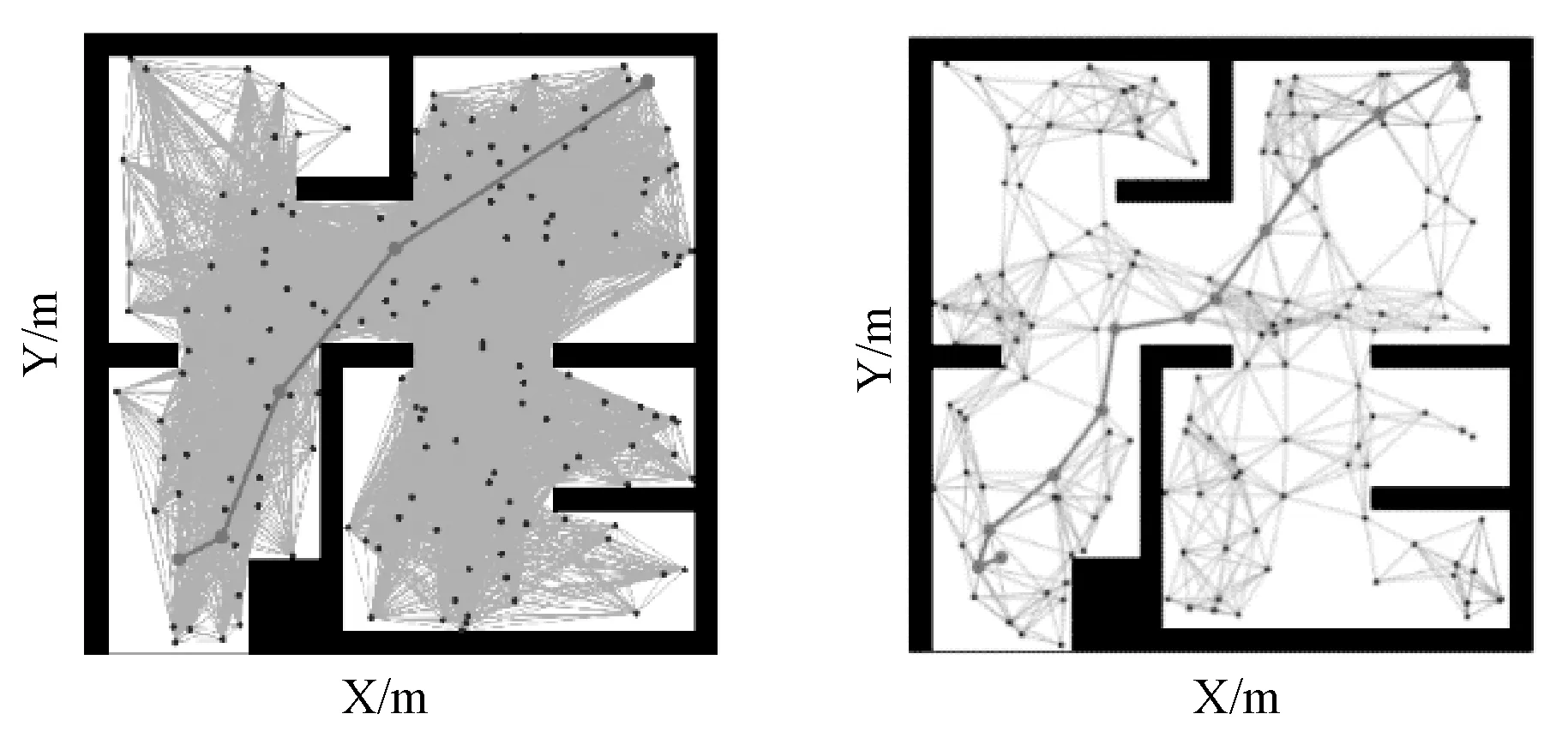
(a)简单障碍物地图优化前 (b)简单障碍物地图优化后

当采样点N=300时，优化前图像如图7(a)和图7(b)所示，优化后结果如图7(c)和图7(d)所示。

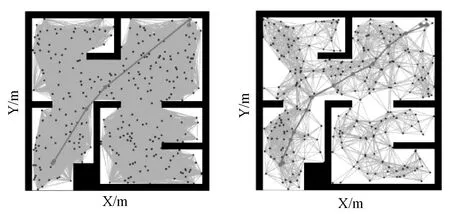
(a)简单障碍物地图优化前 (b)简单障碍物地图优化后

3.2 算法优化前后仿真成功率分析

成功的路径规划才是路线安全的根本，因此为了验证改进算法的成功率，对复杂地图进行改进，增加多个障碍物，使障碍物密度大大提高，能够充分地测试算法的有效性和成功率，改进的复杂地图如图8所示。在地图中固定采样点为150个，对算法优化前后分别进行150次重复性实验。改进的复杂地图仿真结果如图9所示。

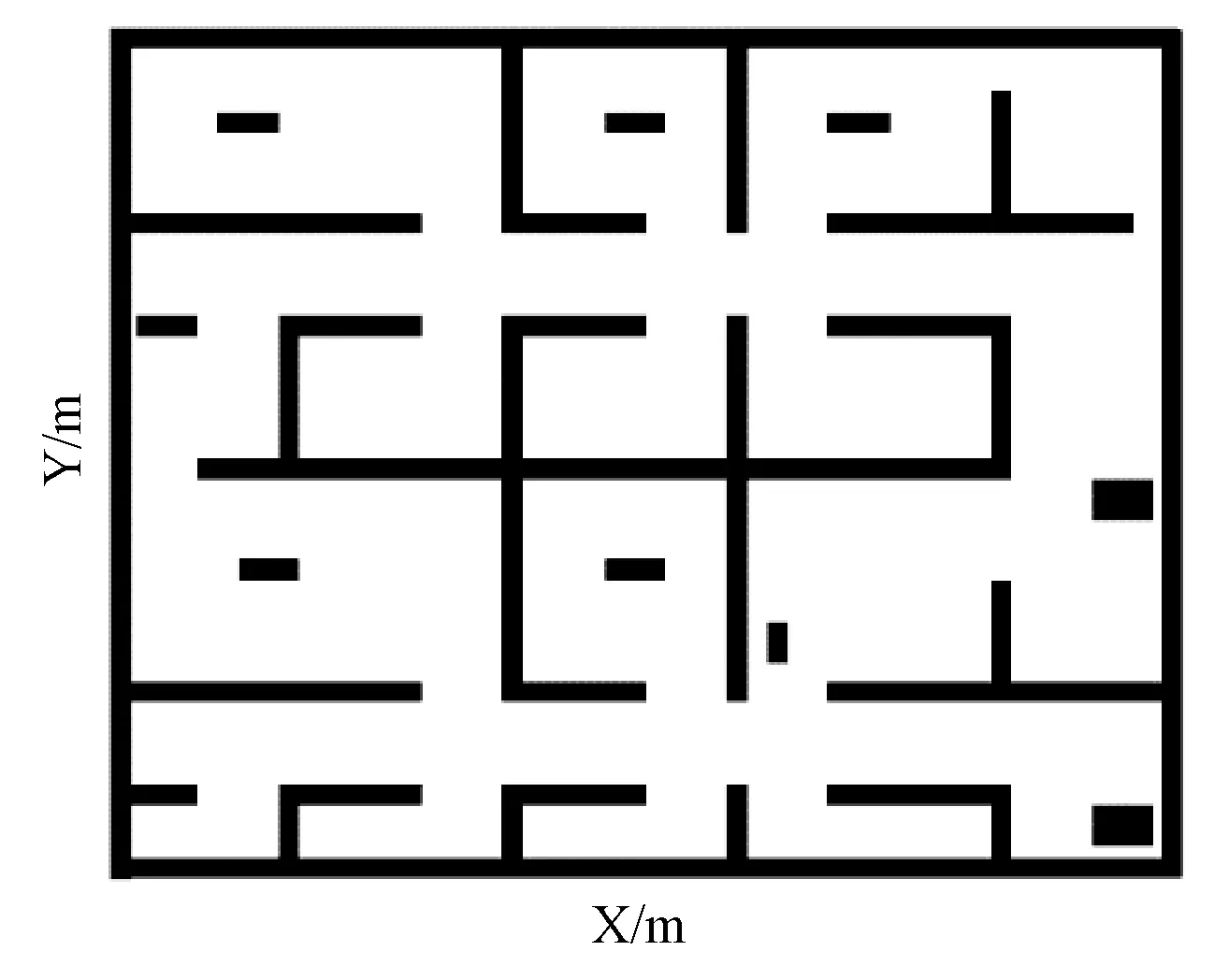
图8 改进的复杂地图

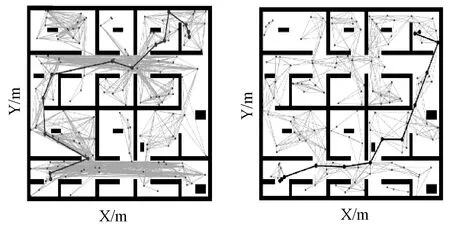
(a)优化前PRM算法 (b)优化后PRM算法

3.3 结果分析

仿真结果如表1所示。采样点个数可以决定能否规划出路径，采样点数量越多，成功规划出路线的概率越大，特别是复杂地图中，如果采样点过少，则可能规划不出路径，导致任务失败。在采样点相同时，优化后的PRM算法与PRM算法相比，时间最大缩短了近50%，且随着采样点数量的上升愈发明显。在安全性上对比，改进后算法距障碍物最短的安全距离要远远大于改进前，使得路线更加可靠。由表2可知，优化后的PRM算法在同一幅地图相同采样点时，规划路径的成功率有所提升，增强了算法的适应性。综上可得，优化后的PRM算法在时间、成功率和安全性上都有了显著的提高，增强了PRM算法在实际中的实用性。

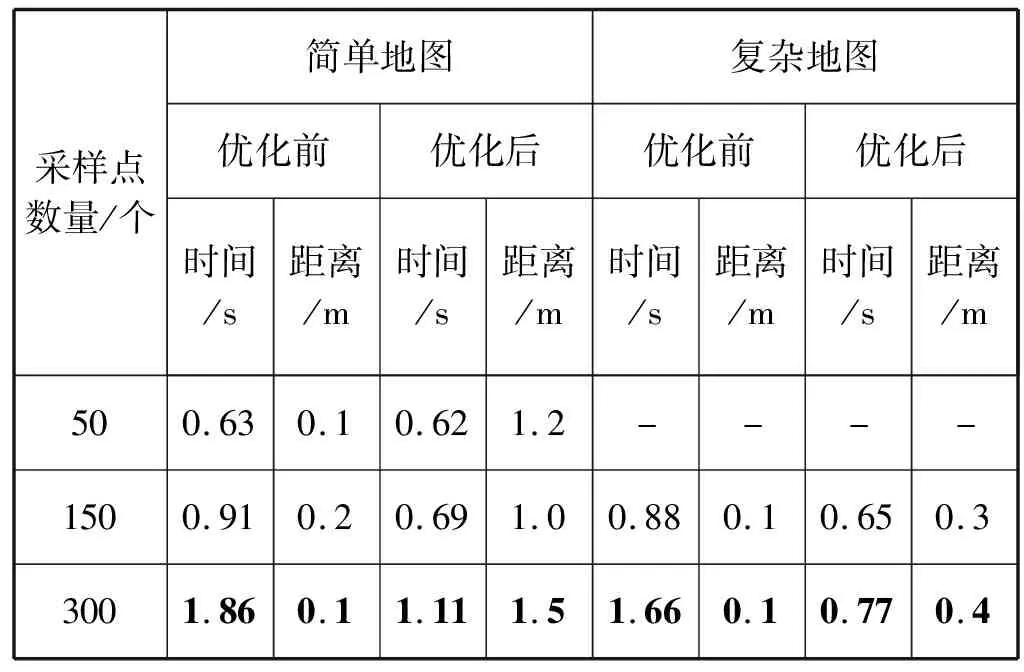
表1 不同地图和采样点优化前后结果

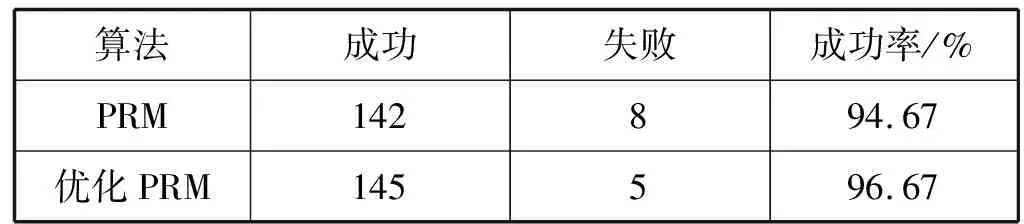
表2 算法优化前后仿真成功率对比

4 基于ROS的仿真分析

为了验证算法实际的应用性，在Linux操作系统上的ROS环境中使用物理仿真平台 Stage 进行机器人路径规划仿真。仿真过程采用的机器人是一个搭载激光雷达可编程的基于 ROS 的移动机器人。在Stage下构建障碍物地图，如图10所示，黑色为障碍物，圆形物体为移动机器人。机器人上搭载激光雷达，可以实时地避障和构建地图，在可视化工具Rviz中可以实时观察到机器人激光雷达实时构建地图，如图11所示，黑色为障碍物。

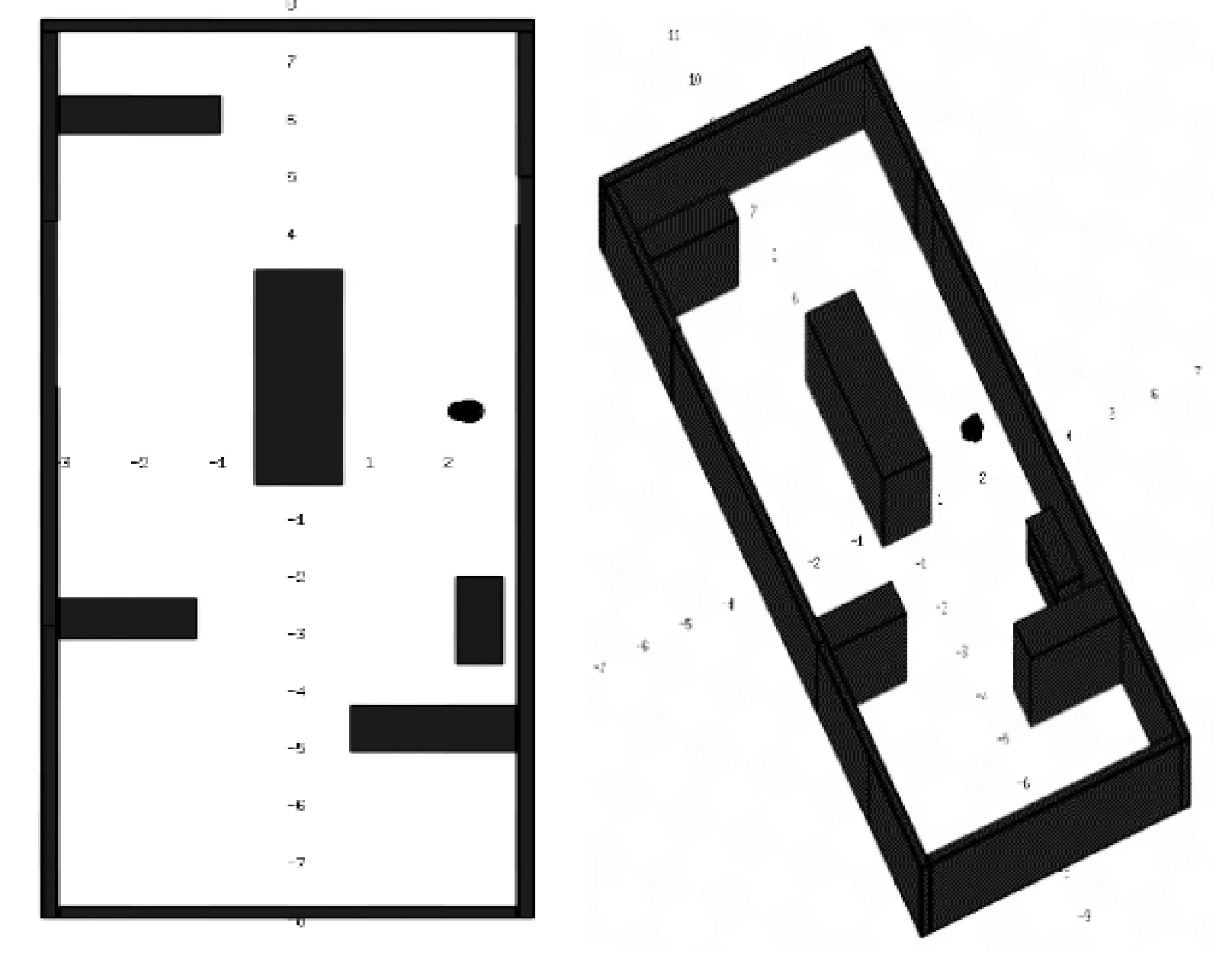
(a) (b)

图11 激光雷达实时构建地图

机器人起始点设为(-1.8，-5.4)，位置如图12(a)所示。终点设置为(-2，3),位置如图12(b)所示。在相同采样点N=150的情况下分别使用PRM算法和优化的PRM算法进行路径优化，PRM算法路径规划结果如图13所示，其中灰线表示所构成的路径网络图。优化前PRM算法的规划结果如图13(a)所示，机器人花费的时间为1.5 s，优化后PRM算法规划结果如图13(b)所示，机器人花费的时间为0.9 s。

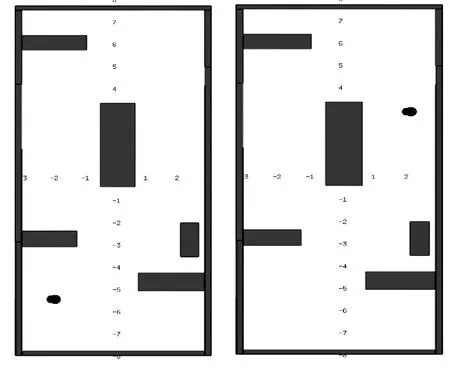
(a)起始点(-1.8,5.4) (b)终点(-2,3)

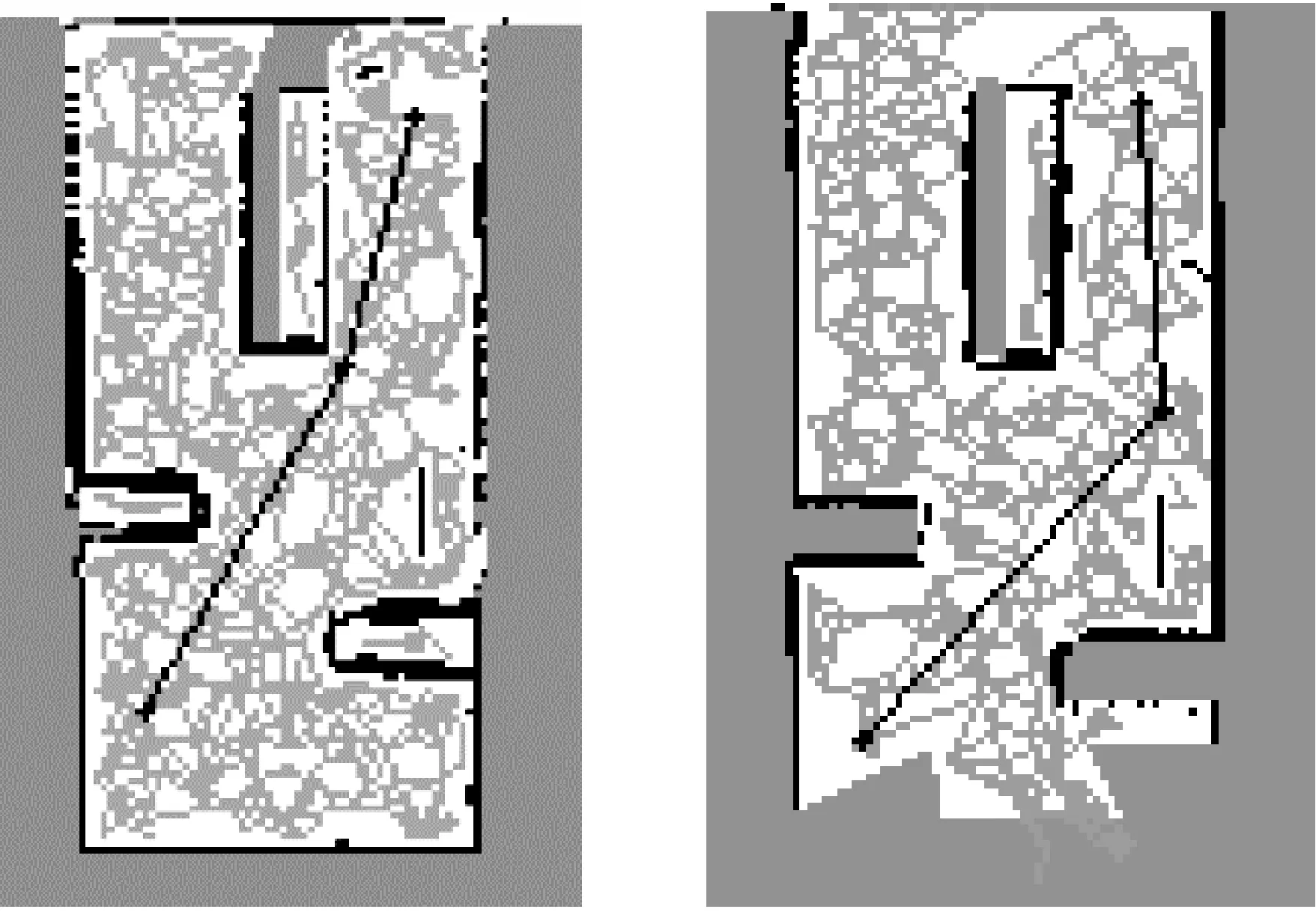
(a)优化前PRM算法 (b)优化后PRM算法

优化后PRM算法较优化前在机器人实时路径规划时所构成的路径网络图明显减少，在搜索效率上有明显改观，并且路径规划的结果较之前在弯道处远离障碍物，安全性明显提升。

为了验证优化算法的成功率，进行了30次重复性实验，实验结果如表3所示，在机器人实际路径规划时优化后的PRM算法较优化前，在花费时间较少的前提下，成功率也有所提升。但实际机器人路径规划成功率因为要考虑数据的误差，以及机器人自身的物理体积，与MATLAB纯算法仿真相比成功率明显下降。

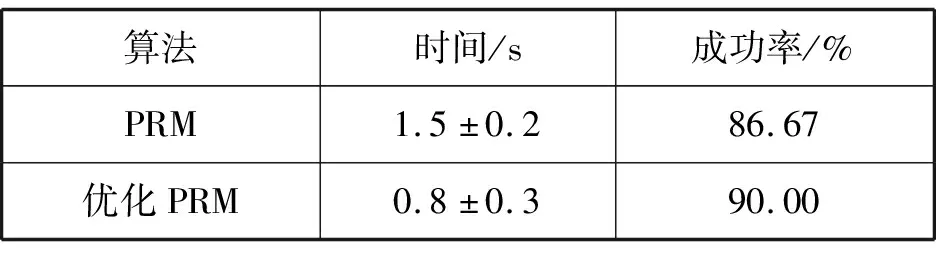
表3 机器人物理仿真结果

5 结 语

本文分析研究PRM算法的原理和过程，针对PRM算法运行速度和安全性进行改进，提出基于连接点距离的改进方法，通过改变连接点的连接距离，减少不合理(如连接点间距离远的情况)的路径，使运行速度有明显的提升，并增加了障碍物的安全距离。本文优化方法应用方便，结构简单，优化后的算法能够有效地提高实时性和安全性，更好地运用在机器人实时路径中。