一个基于鱼群算法的多核系统实时节能调度
张建军 郭伟华
(海军工程大学基础部 湖北 武汉 430033)
0 引 言
能耗已经成为现代实时嵌入式系统设计时需考虑的一个重要因素,特别是电池驱动的无人操控装备、无线移动和便携式计算设备。在保证实时性的前提下,尽可能地降低任务的执行能耗已成为多核系统实时任务调度研究领域的热点。
多核系统的实时节能调度问题已经被证明是一个NP-Hard问题[2]。一般来说,该问题可以归结为以下问题的求解[1]:(1)分配问题,即任务应该在哪一个核上执行;(2)优先级问题,即分配到同一处理器核上的任务的执行顺序问题;(3)动态电压调节(Dynamic Voltage Scaling,DVS)问题,即任务应以何电压级来执行。
目前针对该问题的算法大都基于局部法[3-6]的思想。例如:Pagani等[3]针对周期任务模型,根据能耗最坏情况下近似因子分析,提出一种单频近似方法(Single Frequency Approximation,SFA);Huang等[5]利用EDF算法和片上全局DVS技术,设计了一种简单的静态DVS调节启发式方法。上述调度策略均取得了一定的节能效果,但只考虑了全局DVS,没有考虑对每个核分别进行DVS。
近年来,智能优化算法也逐渐被应用到实时任务节能调度领域并成为新的研究方向。其中,Kianzad等[6]基于遗传算法提出了两种调度策略,一是基于比例分布和并行算法的齐次遗传列表调度并应用静态功率管理的策略(Homogeneous Genetic List Scheduling+Static Power Management with Proportional Distribution and Parallelism Algorithm,HGLS+PDP-SPM);二是综合考虑任务分配、执行顺序和电压调节,并以单个染色体的形式对它们进行编码的整体节能调度框架(combined assignment,scheduling,and power management,CASPER)。以上调度策略均是基于遗传算法研究多核系统的实时节能调度问题,由于遗传算法本身存在着易于“早熟”等问题,因而尽管它们都能取得一定的节能效果,但仍存在着容易陷入局部最优解的突出问题。
李晓磊等[7]通过研究鱼群的行为特点,并应用动物自治体的模型,提出人工鱼群算法(Artificial Fish-swarm Algorithm,AFSA)。其模拟鱼的聚群、追尾等行为,然后选择其中食物浓度最大的行为来实际执行。AFSA是一种有效的寻优算法,与GA相比具有并行性、全局寻优能力强、寻优速度快等特点。
由于同构环境下的多核系统实时节能调度问题本质上是典型的并行计算问题,因而与GA相比,基于AFSA研究该问题具有更强的针对性;另一方面,相比GA,AFSA的全局寻优能力强,基于AFSA研究该问题可以有效避免陷入局部最优。
因此,本文基于AFSA设计一种新的调度策略(Combined Assignment and Power-management basing on Artificial Fish-Swarm Algorithm,CAP-AFSA)。其基本思想是:定义高度值并藉此对任务节点进行优先级排序,以确定执行顺序;对任务分配及电压调节进行整合编码;基于可行性规则处理截止期约束条件,限制寻优方向,以满足系统的实时性要求;在上述基础上对问题进行分析转化,建立相应模型并应用AFSA进行迭代寻优。仿真结果表明,与HGLS+PDP-SPM和CASPER相比,应用CAP-AFSA进行任务调度能得到更好的节能效果。
1 问题模型
1.1 系统模型
本文的多核系统采用模型P={P1,P2,…,Pn}描述,其中Pi(i=1,2,…,n)为同构的处理器核,n为处理器核的个数。同时,将实时嵌入式任务抽象地用有向无环图[8](Directed Acyclic Graph,DAG)描述,并用一个四元组G(N,E,W,D)来表示,其中:任务集N={N1,N2,…,Nm},Ni(i=1,2,…,m)为子任务节点;邻接矩阵E={eij|ti,tj∈T}表示任务节点之间的依赖关系和通信代价,eij=(ti,tj)>0表示ti是tj的前趋节点,tj是ti的后继节点,eij的值表示ti和tj之间的通信开销;W={w1,w2,…,wm},其中wi表示任务节点Ni的估计执行时间(i=1,2,…,m),一般取最坏执行时间;D表示任务截止时间,可根据文献[9]中的方法求得。
1.2 能耗模型
目前大部分嵌入式系统的处理器都采用了COMS集成电路,其功耗主要由静态功耗和动态功耗两部分组成。其中,动态功耗约占总功耗的70%左右[10]。
由于静态功耗占比相对较低,且受所采用的调度策略影响很小,因此本文只考虑动态功耗的影响,采用下述功耗模型[11]:
(1)
式中:Pdyn表示动态功耗;α、k为常数;Cl是电路负载电容;Vdd为电路中处理器核的运行电压;f为运行频率;Vt为门限电压。一般有Vdd>>Vt,即处理器核上的运行频率和电压间近似线性相关。
执行任务节点Ni(i=1,2,…,m)的能耗为:
(2)
式中:ti=Tc(i)/f为任务节点Ni的执行时间;Tc(i)为执行Ni所需的时钟周期数;Vdd(i)为执行Ni的运行电压;Pdyn(i)为执行Ni的动态功耗。可以看出,降低任务节点的执行电压可有效降低动态功耗,但会导致任务的执行时间增加。
本文基于DVS研究多核系统实时节能调度问题,其基本思想是在保证实时性的前提下,通过动态调节执行电压来降低能耗。经电压调节后,我们可将执行嵌入式任务G的能耗表示为:
(3)
上述能耗模型中总能耗只与各任务节点的执行电压与执行所需时钟周期数有关。由于时钟周期数是任务节点的固有属性,与调度策略无关,故只需求得各任务节点的执行电压即可得到总能耗。因而采用本能耗模型便于计算总能耗,进而得到节能效率。
2 策略设计
与GA相比,AFSA的并行性处理及全局寻优能力更强,因而基于AFSA设计调度策略对多核系统的实时节能调度问题这一典型的并行计算问题的针对性更强,且能够有效避免陷入局部最优。
本文基于AFSA设计的调度策略,具体思路如下:
(1)为避免破坏任务节点之间的依赖关系,基于高度值优先级确定执行顺序。
(2)为便于整体化考虑任务分配和电压调节过程,将运行电压离散化处理,从而得到整合任务分配和电压调节过程的新编码方案。同时在模拟行为中进行了取整与越界处理,以确保人工鱼状态向量的合理性。
(3)在问题分析与模型建立中,定义任务节点的开始执行时刻与终止执行时刻,并结合任务节点的执行顺序等限制条件给出计算公式,进而结合分配方案得到任务节点的具体状态。
(4)由于调度问题中存在截止期约束条件,直接应用AFSA迭代寻优所得解不一定可行。因此,本文基于可行性规则处理截止期约束条件,使得寻优过程始终朝着可行、更优的方向前进。
2.1 任务节点的预处理
任务节点的预处理基于以下定义:
定义1对任务节点Ni,定义其高度值h(Ni)[6]为:
(4)
式中:i∈{1,2,…,m};pred(Ni)表示Ni的前趋节点。
本文基于高度值优先级,采用以下策略对任务执行顺序进行排序:
(1)对任务图G,由式(4)求出任务节点Ni的高度值h(Ni)(i=1,2,…,m),再将任务节点按其高度值升序排序,并重新编号,仍记为N1,N2,…,Nm;(2)当两个任务分配到同一处理器核上时,编号小的任务优先执行。
2.2 基于AFSA的算法设计
2.2.1人工鱼行为描述
在本文中,用X表示人工鱼的位置向量;用η=f(X)表示人工鱼当前所在位置的食物浓度,用以表示节能效率;visual表示人工鱼的感知距离;step表示人工鱼移动的步长;delta表示拥挤度因子。
用以下方式描述觅食行为:设人工鱼当前状态为Xi,在其感知范围内随机选择一新状态Xj:
Xj=Xi+visual·rand
(5)
如果ηi<ηj,则向Xj前进一步:
(6)
式中:Xnext表示人工鱼移动后的位置向量。
否则,重新选择新状态Xj进行尝试。反复尝试try_number次后,若仍无法前进,则随机移动一步。
聚群行为则描述如下:设人工鱼当前状态为Xi,探索其感知范围内的人工鱼个体数nf及中心位置Xc。若ηc/nf>delta·ηi,表明该中心位置食物充足且不拥挤,则朝该中心方向前进一步:
(7)
否则执行觅食行为。
追尾行为可表示为:设人工鱼当前状态为Xi,探索其感知范围内的食物浓度最高的人工鱼个体状态Xj。若ηj/nf>delta·ηi,表明Xj位置食物充足且不拥挤,则朝Xj的方向前进一步:
(8)
否则执行觅食行为。
2.2.2编码策略及其取整与越界处理
为整合任务分配过程和电压调节过程,并将它们编码进同一条人工鱼的位置向量中,本文选择将核上的运行电压Vdd离散化处理为k个电压级别{V1 X=(x1,x2,…,xm,xm+1,xm+2,…,x2m) (9) 式中:X的前m个分量表示任务分配策略:xi=j表示将第i个任务节点分配到第j个处理器核上;X的后m个分量表示任务执行电压选择策略:xm+i=j表示以电压Vj执行第i个任务节点,即有: (10) 由于X的分量分别表示任务分配策略和执行电压级选择策略,均为有界的正整数,因而在执行聚群、追尾等行为时,所得到的新状态必须进行取整和越界处理,以保证模拟行为的可行性。 以聚群行为为例,式(7)中的Xnext首先需取整为: (11) 再进行越界处理: (12) 式中:j∈{1,2,…,m}。 2.2.3问题分析与模型建立 基于DVS的多核系统实时节能调度问题的本质是在保证任务实时性的基础上进行任务分配、执行顺序和执行电压的选择以最小化能耗,是一个有约束优化问题。 由于任务节点Ni的估计执行时间wi与执行任务节点所需的时钟周期数Tc(i)成正比,由式(3)可得: (13) 式中:a为常数。 不妨假设未经电压调节前任务均以最大执行电压执行,即未经电压调节前的任务执行能耗为: (14) 式中:(Vdd)max为处理器核上最大执行电压。 从式(13)-式(14)可见,对给定的任务图,调度策略对能耗的影响由各任务节点的执行电压选择唯一确定,进而节能效率可由各任务节点的执行电压表示。 命题1节能效率可表示为: (15) 定义2对于任意人工鱼的状态向量X,定义任务分配的关联矩阵A为: (16) 式中:i∈{1,2,…,m};k∈{1,2,…,n}。 关于任务节点的开始执行时刻与终止执行时刻,有以下结论: 命题2记任务节点Ni(i=1,2,…,m)的开始执行时刻为Tb(i),终止执行时刻为Tf(i)。则: (17) (18) 式中: (19) 若Qji=1,说明任务节点Ni、Nj分配到不同的处理器核上;若Qji=0,说明任务节点Ni、Nj分配到同一个处理器核上。 证明:由任务调度需满足以下规则: (1)任务节点的执行顺序要满足DAG上的依赖关系,即任意任务节点必须在其前趋节点全部执行完毕后执行; (2)任意处理器核的利用率不超过1,即一个处理器核上不可同时执行多个任务节点。 由上述规则即可推得结论。 命题3多核系统的实时任务节能调度问题可归结为具有实时性约束条件的节能效率最大值问题,可表示为: (20) 式中:D为截止时限。 2.2.4基于可行性规则的截止期处理方案 针对相应的有约束最大值问题如式(20),为确保所设计的调度策略满足约束条件,本节基于可行性规则,即可行解始终优于不可行解这一原则处理截止期约束条件,对迭代寻优过程限制如下: 记人工鱼i当前状态为Xi,节能效率为ηi,完成时间为Ti;模拟行为所得状态为Xnext,节能效率为ηnext,完成时间为Tnext。基于可行性规则,当以下三种行为中任意一种发生时,均说明Xnext状态优于Xi状态,执行模拟行为: (1)Ti>D且Tnext≤D:Xi不可行,Xnext可行,表示可行解始终优于不可行解; (2)Ti≤D,Tnext≤D且ηi<ηnext:Xi和Xnext均可行,且Xnext节能效果更好,表示节能效率高的可行解状态更优; (3)Ti>Tnext>D:Xi和Xnext均不可行,但Xnext完成时间相对较小,表示执行时间相对较短的不可行解状态更优。 首先,计算给定任务图G上所有任务节点Ni的高度值h(Ni)(i=1,2,…,m),基于高度值升序排序并重新编号,仍依次记为N1,N2,…,Nm。其次,根据编码方案生成初始鱼群,并计算各人工鱼相应的节能效率η和完成时间T,将其中状态最优的个体赋给公告板。基于可行性规则进行迭代寻优,得到最优状态X0、相应的节能效率η0、完成时间T0并生成迭代曲线。最后,计算任务节点Ni(i=1,2,…,m)开始执行时刻Tb(i)与终止执行时刻Tf(i),对最优状态X0进行解码,得到执行结果图。 算法1CAP-AFSA调度策略 输入:任务图G(N,E,W,D),处理器核的个数n,k个电压级别Vdd={V1 输出:公告版状态X0,节能效率η0,完成时间T0。 Step1对任务节点进行预处理,计算任务节点的高度值,并按其高度值升序排序,并重新编号,仍记为N1,N2,…,Nm。 Step2生成初始鱼群,代码如下: fori=1:Nfish forj=1:m X(i,j)=round(rand(1,1)*(n-1))+1; %任务分配 end forj=m+1:2m X(i,j)=round(rand(1,1)*(k-1))+1; %任务执行电压级选择 end end 并记迭代次数gen=1。 Step3公告板赋初值:计算初始鱼群中各人工鱼的节能效率η和完成时间T。如果∃T≤D,比较所有满足T≤D的状态X的节能效率η大小,取η最大的鱼赋值给公告板;否则取T最小的鱼赋值给公告板。 Step4检查gen是否小于最大迭代次数,如果gen小于最大迭代次数,转至Step 5;否则转至输出,算法结束。 Step5行为选择:各人工鱼模拟追尾、聚群等行为,基于可行性规则选择状态更优的行为实际执行。 Step6公告板更新:各人工鱼基于可行性规则比较自身新状态与公告板状态,如果自身新状态更优,则将自身新状态赋给公告板。记gen←gen+1,转至Step 4。 本文在Windows 8.1系统环境中用MATLAB 2018b编程实现了提出的CAP-AFSA调度策略,并采用上述系统模型及经典实例[6]进行仿真实验以验证算法的有效性。 仿真实验采用的处理器模型包含6个同构的处理器核,其中每个处理器核都能独立地调整执行电压,且有4种离散电压模式,分别为(1.75 V,1 000 MHz)、(1.40 V,800 MHz)、(1.20 V,600 MHz)和(1.00 V,466 MHz);并采用以下5个经典的测试任务图(它们分别表示相关类别的应用问题),其中:RG1[12]是一个具有通信成本的优先图;RG2[13]是使用模型G(Γ,→,μ,η)的一个任务图例;RG3[14]是基于高斯消元法求解含4个变量的四个方程的实现过程;RG4[14]是适应PDG(程序依赖图)的一个物理算法;RG5[15]是拉普拉斯变换的一种实现。 CAP-AFSA的参数设置为鱼群规模Nfish=500;最大迭代次数为200;最多试探次数try_number=100;感知距离visual=5;拥挤度因子delta=0.618;步长step=1。 以RG5为例,介绍CAP-AFSA迭代寻优的过程。 (1)基于高度值优先级对任务节点进行预处理,得到各任务节点的高度值和新编号,结果如图1所示。 图1 RG5中任务节点的预处理 (2)应用CAP-AFSA进行迭代寻优,经迭代200次后,所得公告板状态为: X0=[6,1,6,2,3,4,6,6,2,3,4,2,2,3,4,3,3,4,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1] (21) 节能效率η0=67.35%,完成时间T0=480。 节点开始执行时刻Tb与终止执行时刻Tf分别为: Tb=[0,140,80,140,140,140,120,180,240,240,240,270,310,370,370,390,410,470] Tf=[80,180,120,180,180,180,180,210,270,270,270,310,330,390,390,410,420,480] (22) (3)结合任务节点的开始执行时刻Tb和终止执行时刻Tf对所得公告板状态X0进行解码,得到执行方案如图2所示,迭代曲线如图3所示。 图2 CAP-AFSA调度RG5所得执行方案 将HGLS+PDP-SPM、CASPER与本文调度策略所得结果进行比较,结果见表1。可以看出,CAP-AFSA执行每个任务图的节能效率均优于HGLS+PDP-SPM与CASPER,且相对HGLS+PDP-SPM平均节能效率提高了约10.9%,相对CASPER平均节能效率提高了约4.2%,说明CAP-AFSA调度策略节能效果较好。 表1 CAP-AFSA与相关调度策略节能效率比较 应用CAP-AFSA调度RG1~RG4的迭代寻优曲线分别如图4至图7所示。 图4 CAP-AFSA调度RG1的迭代寻优曲线 图5 CAP-AFSA调度RG2的迭代寻优曲线 图6 CAP-AFSA调度RG3的迭代寻优曲线 图7 CAP-AFSA调度RG4的迭代寻优曲线 可以看出,应用CAP-AFSA调度RG1、RG2、RG4的迭代曲线分别在节能效率达到60.7%、54.3%、62.2%的附近时寻优过程暂时停滞,而后均跳出该点并进一步迭代寻优。因此,可以认为执行RG1、RG2、RG4的节能效率局部最优值分别位于60.7%、54.3%、62.2%附近,这恰好是应用CAPSER执行RG1、RG2、RG4所得的节能效率。可见,应用CAP-AFSA寻优时有效地跳出了局部最优,而应用CAPSER寻优时陷入了局部最优。上述仿真结果表明,与GA相比,AFSA的全局寻优能力更强,从而应用CAP-AFSA能较好地跳出局部最优。 本文针对基于GA的调度策略HGLS+PDP-SPM、CASPER存在的易陷入局部最优等突出问题,基于有约束的AFSA,研究多核系统的实时节能调度问题。通过定义并基于任务节点的高度值确定任务的执行顺序;对任务分配和电压调节进行有机的整合编码;对人工鱼位置向量进行取整和越界处理;基于可行性规则处理截止期约束以保证模拟行为的可行性,进而限制寻优过程等一系列过程,建立有效的问题模型,并应用AFSA进行迭代寻优。仿真结果表明,与HGLS+PDP-SPM、CASPER相比,应用CAP-AFSA执行任务图可以获得更好的节能效果,其总体性能有较显著的改善,因而不失为一种有效的、更具应用性的实时节能调度策略。下一步工作将集中于对更为复杂的多核系统的实时节能调度问题模型进行研究。2.3 CAP-AFSA描述
3 仿真实例与结果分析
3.1 实例求解


3.2 仿真结果及其分析


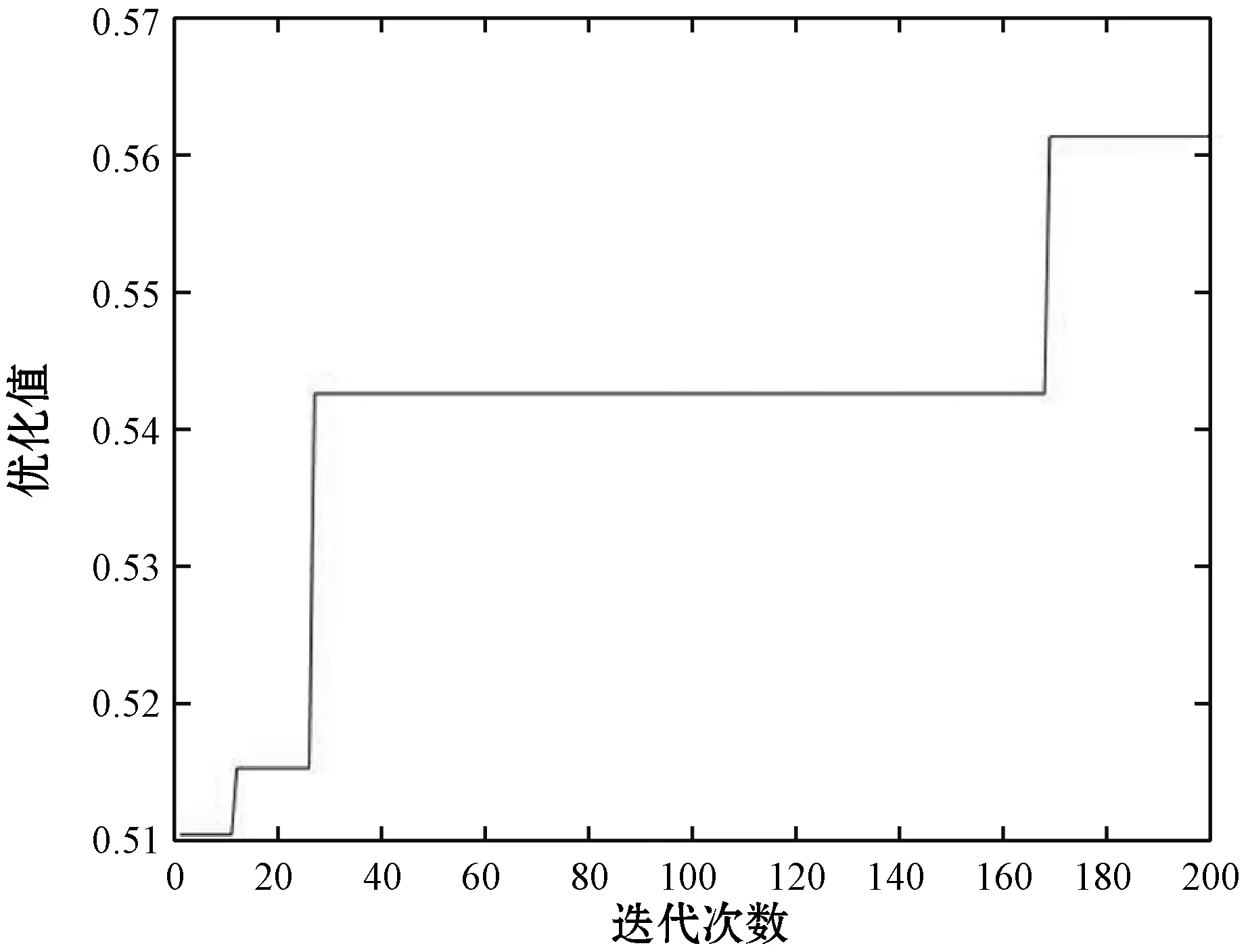
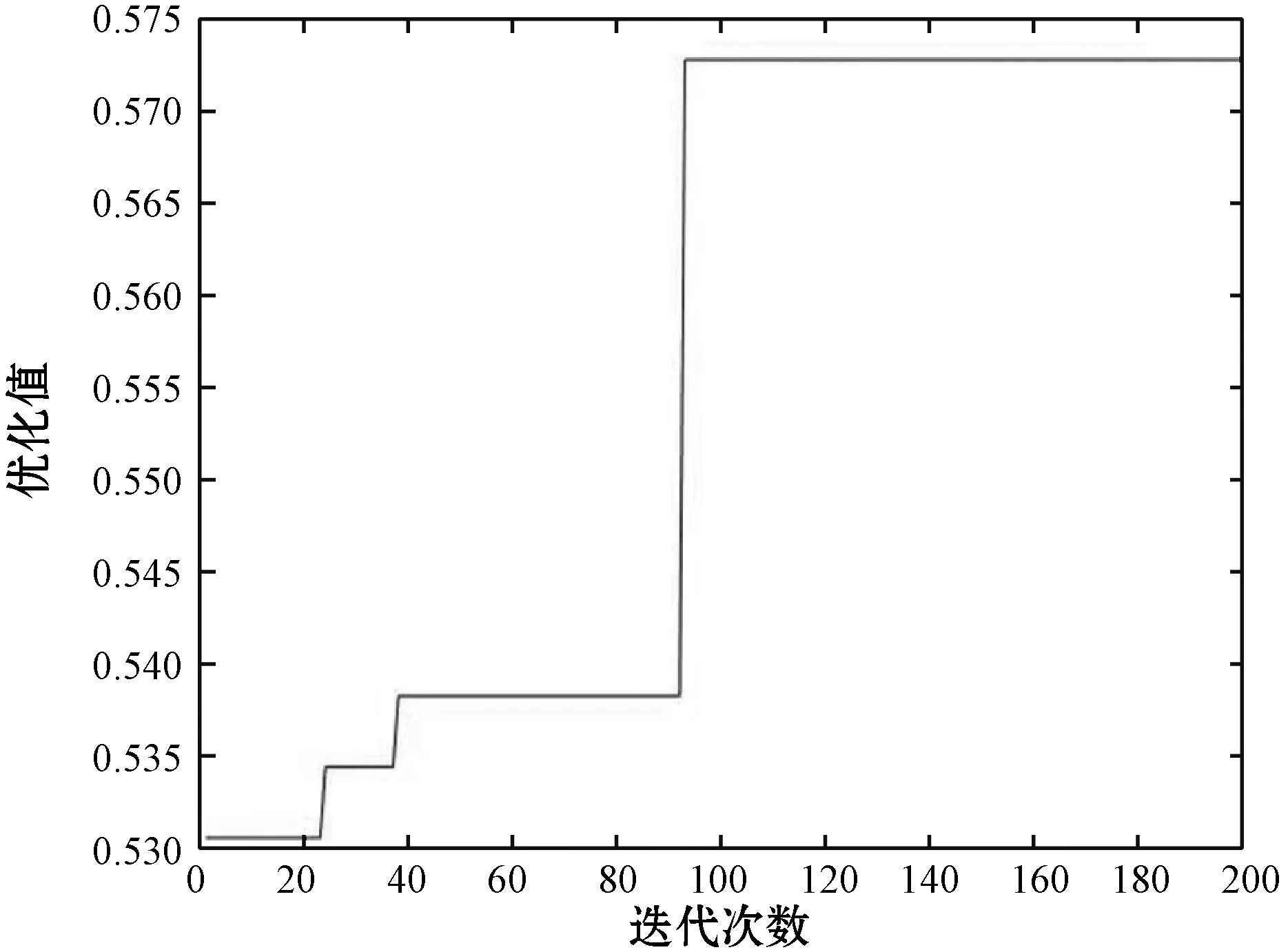

4 结 语

