基于灰度波动的非均匀光照文档图像二值化
王刘奎 史伟民 杨亮亮,2*
1(浙江理工大学机械与自动控制学院 浙江 杭州 310018)2(杭州汇萃智能科技有限公司 浙江 杭州 311121)
0 引 言
近年来随着科学技术的不断发展,工业自动化水平的逐步提高,机器视觉图像处理领域受到了人们的广泛关注,成为了大量学者研究的焦点。文字字符识别在信件邮寄识别、历史文献修复、汽车车牌识别等有关文字的应用领域占据着至关重要的地位,而较好地把文本信息从实际情况较复杂的背景中分割出来则是视觉检测预处理中最重要的部分,其中文本二值化是必不可少且极其关键的。而在实际拍摄过程中,由于光源方向、拍摄角度、物体表面反射等因素,往往使得采集的图像出现局部过亮、局部过暗、明暗交错等光照不均匀现象,严重影响后续处理,完整有效地提取出高质量的文本信息无疑对整个项目的成败起着关键作用。
为了把文字从光照不均匀的背景中提取出来,阈值分割是最常用的方法,按照参与运算的像素点的空间范围可分为全局阈值分割法和局部阈值分割法[1]。
全局阈值分割法根据整幅图的直方图或灰度值的空间分布来计算出一个阈值[2],依此来区分目标和背景,经典的全局阈值算法有Ostu法、迭代法、最小误差法、简单统计、基于熵的阈值法等[3]。由于全局阈值分割法未考虑图像的局部灰度信息,对背景和目标灰度值多样性单一,存在明显差异、直方图呈现双峰分布的图像处理效果良好,而对灰度分布不均匀、峰值多样无规律的图像处理效果非常差[4]。
局部阈值分割法按处理思想不同又可细分为局部分块阈值法和局部邻域自适应阈值法[5]。局部分块阈值法根据图像光照情况进行分块,再对每块进行全局阈值分割法进行分割。该方法需要图像存在较明显的灰度边界区域,对于灰度差别不明显的图像处理效果欠佳[6],而且处理后存在明显分块边界,整体效果差,在文档二值化处理中应用不广泛。
局部邻域自适应阈值法通过定义合适的模板,并通过模板邻域点与考察点的数学关系进行运算,来确定当前考察点的灰度值,该方法很好地利用了考察点的邻近区域的灰度特性,实现了自适应阈值检测。经典的局部阈值分割法有Niblack法[7]、Bernsen法[8]、Sauvola法[9]等,以上方法虽然考虑了局部邻域灰度信息,但参与运算的不具有代表性的像素点过多,当目标和背景区分界线不明显时,分割效果不佳,而且容易出现笔画断裂和伪影现象。Wellner[10]提出了一种根据每点距离像素中心位置不同加权不同,最后求均值乘以比例系数确定阈值的思想。针对该算法边缘和处理速度慢的问题,Bradley等[11]提出了一种面积像素表求和的思想,极大简化了运算,提高了速度,处理效果极佳。Valizadeh等[12]通过把图像灰度值类比三维地形提出了Water Flow模型理论,山峰对应灰度值较高区域,山谷对应灰度值较低区域,地形的差异使得光照在不同地形情况呈现了光照不均匀现象。
本文仔细研究了以上方法,并在观察不均匀文本图像灰度值曲线的变化规律后,发现光线非常均匀的部分邻近灰度值不变,基本上都是背景或者文字比划部分,在运算时已经大量重复。而灰度跳跃明显的区域多是文字和背景的交界区域,包含了大量的文字边缘轮廓信息。对于所需的灰度值跳跃的点,本文在一个邻域里比较筛选出所有波峰点和波谷点求均值后,再通过一定差值比例加权运算选出最佳的阈值分割点,结果表明处理效果优于传统局部阈值分割算法。
1 经典局部邻域自适应阈值法分析
1.1 Niblack算法
Niblack算法是通过当前目标考察点及其模板算子邻域内像素点灰度值的平均值及标准差数学运算后得到二值化阈值。在确定图像的二值化时,先计算以(x,y)为中心的n×n大小的邻域内像素点的灰度平均值m和标准差s:
(1)
(2)
二值化阈值T(x,y)的计算公式如下:
T(x,y)=k·s(x,y)+m(x,y)
(3)
式中:k是根据经验预定的修正系数,一般k取0.1~0.5。
当前观察点的最终阈值由以下公式决定:
(4)
该算法考虑了观察点的模板邻域均值和标准差信息,但存在以下缺点:
1)伪影现象。该算法虽然考虑了均值和标准差,但个别的椒盐噪声点将引起阈值的突变,本是背景的点被二值化成目标点,导致伪噪声的引入。
2)笔画断裂现象。当模板窗口内都为目标点时,局部阈值拉伸,本是目标的点却被二值化成背景,使得信息丢失,从而出现笔画断裂现象。
Sauvola算法在Niblack算法基础上,引入了标准方差的动态范围R,虽然有效地抑制了伪影现象和笔画断裂现象,但仍有不少噪声点无法去除。
1.2 Wellner算法
设模板邻域为s×s的方阵,图像中点Ps×s(x,y)周围邻域的像素值的总和为:
(5)
设t为修正系数,T(x,y)为点考察点Ps×s(x,y)最终的像素值,则:
(6)
在实际测试中s=image.width/8,而t=15时效果最好,在确定T(x,y)的值时,用的是平均值,但由于当前点的灰度值跟其附近邻域点有关,改成距离考察点Ps×s(x,y)越近的像素点对其的影响越大,越远则越小,则更加具有说服力,为了便于理解将式(6)简化为:
(7)
(8)
这里需给定初始迭代值,取T(n)=127×s,Wellner算法无法处理边缘图像,Bradley等[11]改进了Wellner算法:以图像当前考察点为基准,把该点左上方所有的像素值累加重新赋值给该点,边界点按水平或者竖直方向处理,处理过程如图1所示,其中33即为所有像素总和。

(a) (b)
像素总值面积表如图2所示。要判定区域D时,就可以利用图1(b),设P(x,y)为点(x,y)的像素值(已转换为图1(b)的值),对于区域D的总阈值为:

图2 像素总值面积表
P(D)=P(x2,y2)-P(x2,y1)-
P(x1,y2)+P(x1,y1)
(9)
得到区域D的总阈值,再除以区域D的像素点个数得到平均阈值Pjun=P(D)/N,对于区域中心点(i,j)若P(i,j)>P,则重写点(i,j)的像素为255,反之为0。
改进后的Wellner算法很好地解决了边缘处理问题,而且创新地提出了面积制表的思想,极大地提高了处理速度。
2 投影方向灰度曲线波动阈值分割
2.1 不均匀光照图像特性分析
实际的图像采集过程中,现场环境复杂多变,受拍摄角度、物体表面反射率、光源照射方向、光源与物体距离、相机成像系统等影响,最终的图像往往呈现出离散、无规律、明暗相间等不均匀光照现象,严重影响了图片的质量,为后续的处理带来了极大的困难。
图3是大小为773×443的文本图像,为左侧光源打光,左侧有物体遮挡,光线较暗,背景灰度值较低,中间局部区域光源斜角度直射,灰度值较大,右侧区域随着距光源的距离逐步拉远,灰度值逐渐降低,整幅图的背景灰度值大小不一。图4为其灰度直方图。可以看出,波峰和波谷交叉出现,且没有规律,若采用单一的全局阈值来分割,左部区域灰度值会被置0,中部的部分区域灰度值将会置255,最终无法均衡整个区域,导致分割失败。但在不同的局部小范围区域,存在明显的灰度值差异,肉眼仍可分辨出背景和目标,采用“局部范围相对阈值分割”,仍可得到很好的阈值分割效果。把图3局部区域放大如图5所示,该区域每个点的灰度值大小不一,高低起伏,每个点的灰度值,不仅与自身的二维平面位置、该点物的表面光线反射率等有关,还与其自身相邻域的点的灰度特性有关,灰度值较低的点,附近点的灰度值也会受其影响相应较低。该目标考察点显示出的灰度值是多种因素共同造成的结果,实际分割时,应把邻域的像素点考虑进去。为了更直观地分析图像灰度曲线波动情况,绘制原始图的局部区域三维灰度特性如图6所示。

图3 文本原始图
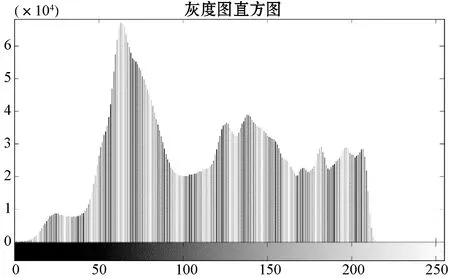
图4 原始图的灰度直方图

图5 原始图的局部放大图

图6 原始图的三维灰度波动图
把图像的三维图和连绵不断的波峰波谷地形进行类比[13],图3中跳跃突变的亮点对应着三维图中的波峰点,对应着地形上的覆盖白雪的山顶;跳跃突变的暗点对应着三维图中的波谷点,对应着地形上的黑暗深渊的山谷。图像的三维灰度特性图之所以呈现空间三维地形,是受物体表面不同区域的光线反射率影响,不同的光线反射率相当于不同的地形,表现在图像上就是灰度值不同。
2.2 投影方向灰度曲线波动思想
实际图3中的突变亮点一般是夹杂在黑色字体之间的白色背景,突变黑点一般是夹杂在白色纸张背景之间的黑色文字边缘,且突变较大。白色背景和黑色字体是有宽度的,中间的部分较亮或较暗,因而内部也会产生小尺度的灰度波动,但突变较小。选取图3文本图像的中间行即第222行,统计前433个像素,以像素点在当前行数的位置为横轴,以灰度值为纵轴绘制曲线如图7所示。

图7 第222行的前433像素点灰度变化曲线图
可以看出,灰度值曲线上下起伏,变化频繁剧烈,整体灰度值越来越高,与实际的光照情况相吻合。另外灰度值均匀降低的点对应曲线的斜率为负的直线部分;灰度值均匀上升的点对应曲线的斜率为正的直线部分;灰度值不变的点,反映在曲线上是一条直线。产生均匀斜线的原因是背景变化较均匀(白色纸张或黑色文字邻近边缘,如果斜线部分斜率为正整体灰度值逐渐增大即是白色背景纸;斜线部分斜率为负整体灰度值减小且变化剧烈即是黑色文字邻近边缘),这些较均匀斜线直线部分绝大多是背景,基本不包含文字的轮廓和位置信息,对附近像素点的灰度值影响较小,不考虑加入算法。而图中曲线峰值点为图像文字与文字之间或文字内部的白色背景,灰度值较大,曲线峰谷点为文字笔划中心,灰度值较小。
波峰波谷包含了详细的文字边缘信息,不同的波峰点和波谷点,反映了不同文字的不同边缘变化趋势,灰度值与其在曲线上的波动坐标相互对应,而且上述分析得出波峰和波谷点对当前点的最终表现的灰度值影响更大。那么若已知当前目标考察点的某一方向的灰度变化曲线,提取了所有的波峰点和波谷点,所选的判定阈值应该在波峰波谷之间动态浮动,满足一定的关系。
本文在水平方向上某一行选择长度为L的一段条形区域,考虑到图像边界问题,可先将图像左右宽度扩展L/2,该区域在当前行水平移动,L的中心点则从选取的当前行的第一个点移动到最后一个点,每次平移选取L区域覆盖的图像部分,以被覆盖的图像像素点在条形区域的位置为横坐标,以灰度值为纵坐标,绘制灰度波动曲线f(x),x=1,2,…,L,L为条形区域长度。图8所示为图3第38行的以(38,38)为中心、L为75的条形区域灰度波动曲线,所有的波峰点和波谷点已全部标记出来,判定阈值T1的选取与这些点有关。本文选择水平方向遍历,实际不均匀光照影响中,竖直方向同样需要考虑进去,同样如上述步骤处理。根据目标点竖直方向灰度波动曲线求出判定阈值T2,最终判定阈值为T=ξ×(T1+T2),将T与当前目标考察点进行比较,依次确定该点灰度值,最后依次完成全图遍历,阈值分割完成。
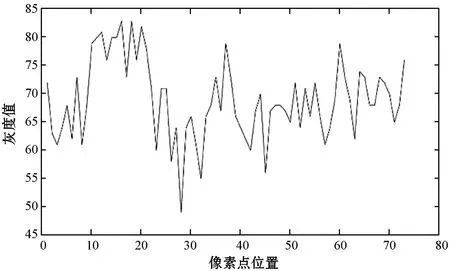
图8 第38行的前75像素点灰度变化图
确定阈值T1和T2的关键在于找到灰度波动曲线上的波峰点及波谷点,在实际中,曲线不仅仅像图8那样上下起伏变化明显,还会出现短暂或者连续的水平直线,即灰度值阶段性重复,此时这些点的灰度值已经重复,不需要把该直线上波峰点或者波谷点都提取出来,所以需要根据实际情况,重新定义波峰点和波谷点。
2.3 波峰点和波谷点的定义
在数学表达式定义中,连续曲线的波峰和波谷就是曲线的极值点,满足一阶倒数为0,并且二阶倒数为负的点为峰值点;满足一阶倒数为0,并且二阶倒数正数的点为峰谷点。但图像的曲线是离散的,应使用求差分函数来求解,确定峰值点和峰谷点,绘制灰度离散图如图9所示。
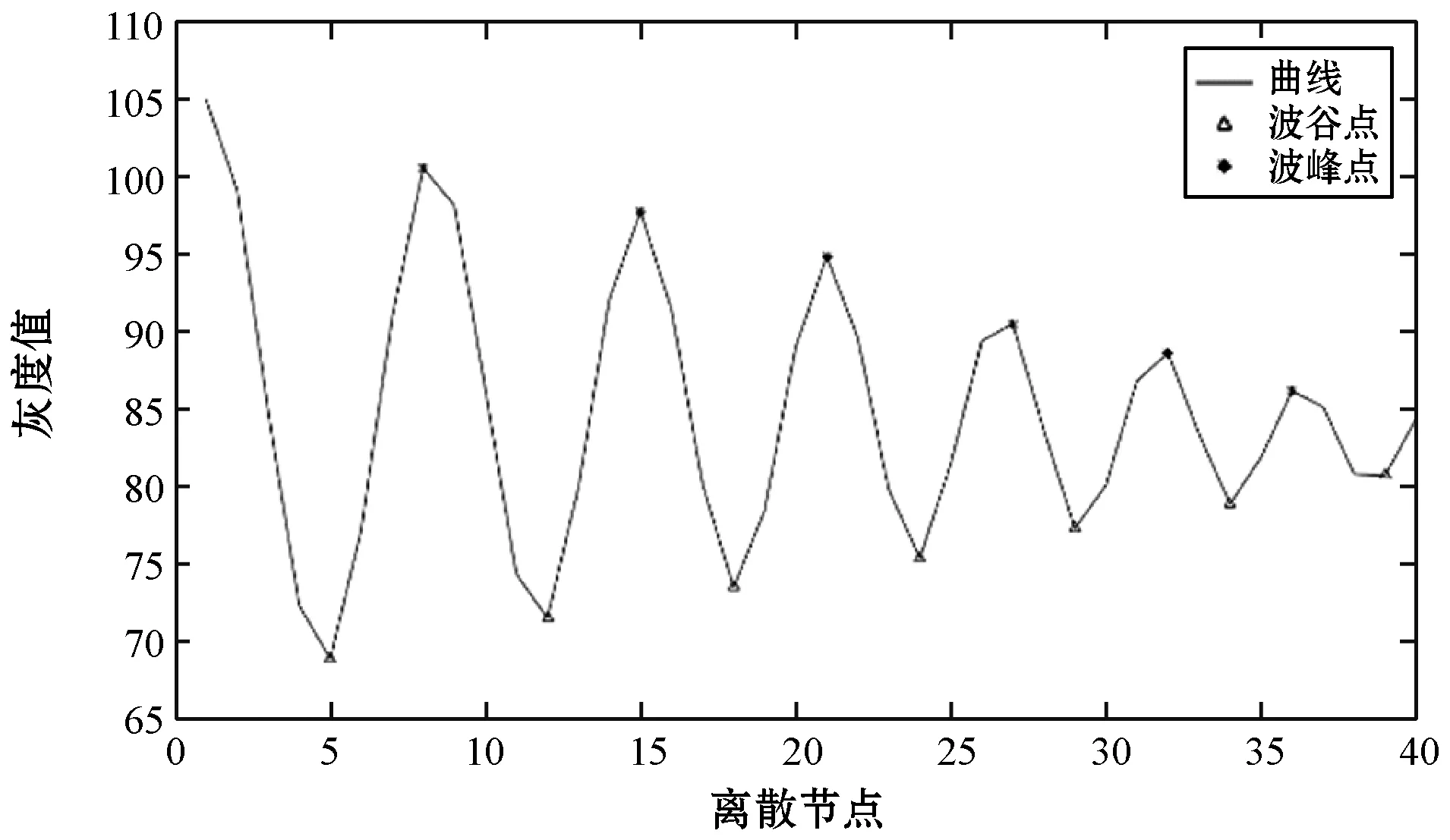
图9 离散点波峰和波谷
依次得到灰度离散图像上每个点所对应的灰度值,对其进行前后差分操作,当前的遍历点前后差分出现相异符号时,便可初步判定其为峰值点或峰谷点,判定依据如下:
(10)
式(10)可以处理平滑的灰度波动曲线,但实际图形曲线会出现如图10所示的情况,式(10)显然是不全面的。

图10 重复的波峰点和波谷点
仔细分析可知,若出现平行的直线且灰度值较大,则为白色背景,灰度值很小,则为黑色文字区域,这种情况,只取第一个点加入即可,避免不必要的重复,这样即可找到所有满足条件的点。
因此当投影曲线是图10所示的曲线类型时,判定依据改为:
(11)
2.4 局部分割阈值判定
通过上述方法最大限度地提取了目标考察点水平和竖直范围内的所有有价值的波峰点和波谷点,它们包含了图像重要的边缘信息,这些突变的点是光照不均匀的直接反映,在考察点长为L的水平邻域内,我们把满足式(11)的水平方向上的点分别存放在一维矩阵A和B中。
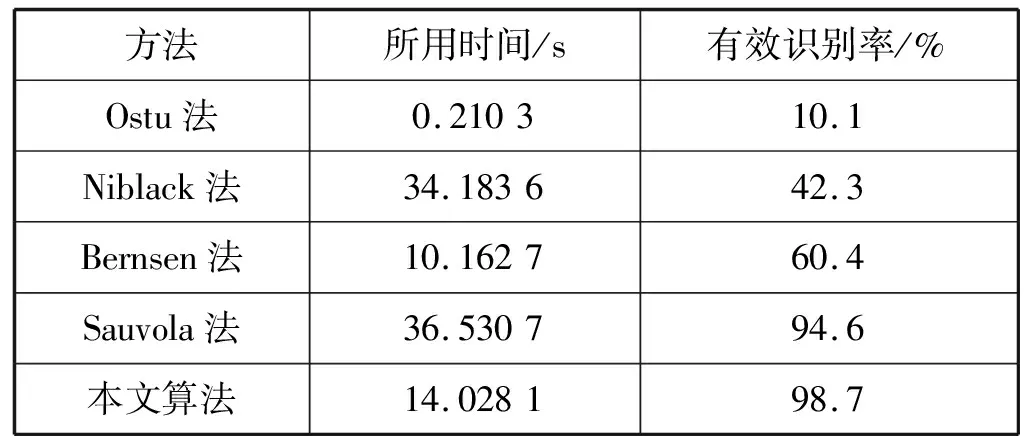
A=[a1,a2,…,ai,…,am-1,am]m B=[b1,b2,…,bj,…,bn-1,bn]n 式中:ai为第i个波峰点的灰度值;bj为第j个波谷点的灰度值。再求波峰点、波谷点的平均值如下: Aaverage=Asum/m (12) Baverage=Bsum/n (13) 式中:Asum为波峰点的灰度值总和;m为波峰的总数;Bsum为波谷点的灰度值总和;n为波谷的总数。则水平方向的阈值判定T1的计算方法为: T1=K(Aaverage-Baverage)+Baverage (14) 同理计算出竖直方向上的局部阈值判定T2,最终阈值如下: T=ξ×(T1+T2)ξ∈[0,1] (15) 若该考察点的灰度值大于T,则灰度值置为255,若灰度值小于等于T,则灰度值置为0,依此可判定改点是属于目标区域还是背景区域,依次对全图循环遍历,得到自适应的二值化图像。 灰度波动曲线阈值分割实现过程如下: 1)首先通过相机拍摄在光源不均匀照射下的图像,再设置十字形模板的长宽L,L过大则运算速度过大,L过小则分割效果不佳。通过大量实验,当L=75左右时,分割效果最好。 2)绘制当前目标考察点为中心的模板内,水平和竖直方向的灰度波动曲线,通过对灰度曲线上的坐标位置对应的图像像素点进行前后差分工作,获取水平和竖直方向上的所有波峰点和波谷点,并把坐标和灰度值存在信息相应的一维矩阵中。 3)计算水平方向的所有波峰平均值和波谷平均值。根据公式得到平均波峰值和平均波谷值之间动态分割阈值T1,同理得到竖直方向动态分割阈值T2,通过加权平均得到最终阈值T。 4)把当前考察点的灰度值和最终阈值T比较,分割为目标或背景,十字模板从图像的左上角依次从左到右、从上到下,循环到右下角,完成全图分割。经过大量不同光照情况的文本实验分析得,K取0.2、ξ取0.4时效果最佳。 实验环境:CPU为Inte酷睿i5 337U,2.7 GHz,内存4 GB,程序编平台为MATLAB 2014b,对光照不均匀的文档图像的二值化阈值分割的编程核心M语言代码如下: for i=H:(height-H+1) %(i,j)程序遍历起点 for j=H:(width-H+1) … for q=(j-(H-2)):(j+H-2) Cpoint(cpoint)=in(i,q) %提取竖直方向H个点的灰度值 if(in(i,q)>in(i,q-1)&& in(i,q)>=in(i,q+1)) A(ii)=in(i,q); end %波峰点数组 if(in(i,q) B(jj)=in(i,q); end %波谷点数组 ii=ii+1; jj=jj+1; cpoint=cpoint+1; end T1=0.2*((sum(A))/averageA-(sum(B))/ averageB)+(sum(B))/averageB; %竖直方向阈值T1 … %同理求出T2 T=(T1+T2)*0.4 %最终阈值T 为了验证本文算法的有效性,选取了具有经典代表性的方法作为对比参照,全局阈值分割法以Ostu法为代表,局部阈值分割法有Niblack算法、Bernsen算法,各算法处理结果对比如图11所示。图11(a)所示为左侧平行光斜角度照射所得的文本图像,尺寸为1 040×780。在对比参照实验中,各算法的相关参数设置如下:Niblack算法中K值取0.2,Sauvola算法中K值取0.36,Niblack和Sauvola算法的模板窗口大小为20×20,本文算法中K的取值为0.2,ξ的取值为0.4。 (a)原图 (b)Ostu算法 (c)Niblack算法 1)算法二值化分割效果及性能对比。由图11(a)可见,左侧区域灰度值较高,右侧区域出现阴影,灰度值较低,全图光照不均匀。从处理效果及算法性能来看,Ostu算法在光照较好的区域效果较好,对于较暗的区域和较亮的区域产生了两极化的处理结果;Niblack算法虽然能分割出文字的轮廓但整个背景区域出现了大量的黑色纹理噪声;Bernsen算法在较亮的区域处理效果还好,在较暗的区域依然会出现大量伪影和噪声;Sauvola算法在Niblack算法上做了改进,考虑了像素点邻域内标准差,处理效果得到了改善,但仍有不少椒盐噪声,尤其是灰度值较低的区域中噪声更加明显;本文算法准确分割出了文字和背景,而且纹理清晰,零噪声,细节保留良好。经过大量不同文本不同光照情况实验,本文算法与最有效的Wellner算法在处理结果上几乎没有差别。结果表明:在不同的光照不均匀情况下,选取同样的阈值,本文算法处理效果和适应性依然较好。 2)参数L、K和ξ的对分割结果的影响。模板邻域区域的长度L的大小直接影响整个算法的处理速度,L选取得越大,运算速度越慢,L选取得过小,文字墨迹发白变浅,像蒙了一层雾。随着L的增大,墨迹逐步加深,所以L的选取既要考虑速度又要考虑效果,经过不同文本光照情况的测试得出L取75效果最佳,字迹最清晰。 ξ的改变不影响运算速度,ξ过小,字迹会淡化,笔画断裂,类似于被腐蚀;ξ越大,字迹轮廓越清晰,但文字会逐渐出现黑色斑点,与Niblack法处理结果很像。当ξ取0.4时,效果最佳。 K的取值与处理后文字轮廓的粗细度有关,K值越大,文字轮廓越明显,过大会出现重影,经过实验K取0.2最佳。 3)处理时间对比。表1是对图11处理结果绘制的表格,给出了Ostu法、Niblack法、Bernsen法、Sauvola法以及本文算法的处理时间。可以看出,Ostu法运算时间是最短的;Niblack法、Bernsen法、Sauvola法三种基于局部邻域像素的算法需要计算均值和标准差,耗时较久,实时性较差;本文算法主要在搜索波峰点和波谷点部分耗时,由于不需要计算标准差,速度有了明显的提升,但由于是MATLAB编程,所以速度和程序优化上有待提高。 表1 五种算法运行性能对比 本文提出了一种针对光照不均匀的文本图像的局部灰度波动的自适应阈值分割算法。根据图像每个像素及其邻域点的灰度值跳动,把图像和三维地形联系起来,图像每一行每一列的灰度波动变化曲线,可看作与之对应的三维地形剖面轮廓图。考虑到阳光造成三维地形朝阳和背阴的现象、光线反射、物体表面反射率等因素,当前点的灰度值受其邻域范围内波峰点和波谷点影响更大。所以本文算法把当前目标考察点的一定范围内水平和竖直方向的所有的波峰点和波谷点提取出来,通过一定的均值加权处理,确定当前点的阈值,完成当前点的阈值分割。实验证明本文方法可以处理不同光照情况的文本图像,自适应强,分割效果较好,充分考虑了光照不均匀的敏感变化点。该算法的不足之处在于:模板尺寸L对处理结果有影响,L过大速度变慢,L过小处理效果不佳;考虑到是全图遍历,提取波峰点和波谷点求平均过程执行速度相对较慢。2.5 灰度波动曲线阈值分割实现
2.6 核心编程的实现
3 实验结果与分析

4 结 语

