基于UWB技术的室内智能跟随系统的实现与优化
刘关迪 赵 璐
(南京工业大学计算机科学与技术学院 江苏 南京 211816)
0 引 言
随着技术的发展和应用场景的扩展,可移动设备的智能跟随需求越来越大。然而目前主流采用的红外传感器、超声传感器等定位方式存在着无法锁定跟随目标,易偏离目标失去定位的问题[1]。这是因为室内环境下障碍物较多,传感器对目标的测距易被障碍物阻挡,导致测量错误;而GPS信号功率低、接收要求高,室内定位时建筑物的阻挡又减弱了信号,导致GPS的定位精度低。因此,设计并实现一种可以精确定位目标、准确自动跟随的系统很有必要。
本文使用UWB(Ultra Wideband)技术实现精确定位,以树莓派小车为移动设备,设计并实现一个实时自动跟随系统,并进一步对系统的可优化性进行讨论。
1 UWB技术简介
UWB是一种无载波通信技术,其脉冲宽度仅为纳秒级或亚纳秒级,拥有数据传输速率高、发射平均功率谱密度低等多种优点。其在定位方面有着两方面优势:
1)由于其窄脉冲特点,定位精度可达厘米级甚至更高。
2)UWB通信采用调时序列,时间分辨率高,具有抗多径能力和一定的穿透能力,适用于高速、低速等不同移动环境[2-3]。
因此,UWB技术凭借其穿透性,可以很好地消除室内障碍物对定位的影响;其信息传送能力良好,测距准确,精度高。该技术的使用解决了传统室内定位方法遇到的困难。近年来,国内外逐渐将UWB技术应用于近距离精确室内定位,IEEE 802.15.4a标准采用UWB为定位首选技术[4-5]。
1.1 室内定位模块
UWB用于室内定位时,需要配置定位标签和定位基站两种模块。
(1)定位标签。定位标签用于配置在需要定位的目标端,是UWB定位的主模块。其体积小,功耗低,可制成或集成于各类穿戴设备中,便于定位目标携带。定位标签为有源电子标签,每个标签具有唯一的ID,可以将目标与ID一对一绑定。
(2)定位基站。定位基站是UWB定位的从模块。基站可以通过飞行时间测距法等多种方法,确定标签的位置,并将数据传输至网络控制器及定位引擎软件,定位精度达到厘米级。
1.2 测距原理
UWB测距使用飞行时间测距法(Time of Flight)。该技术需要在异步收发机(Transceiver)之间有准确的时间同步[6-7],利用射频信号在异步收发机间的飞行时间TTOF转换为两点之间的距离d:
d=c·TTOF
(1)
式中:c为射频信号的传播速度,可认为其等同于真空中的光速。
飞行时间测距法测距流程[8]如图1所示,其中:TX表示发送;RX表示接收。设备A在TsA时刻发送请求脉冲信号,设备B在TrB时刻接收该信号,并于TsB时刻发射响应信号,设备A在TrA时刻接收该响应信号。设定设备A发送脉冲信号和接收到响应信号的时间间隔为Tround,设备B从接收到请求脉冲信号到发射响应信号的时间间隔为Treply,则:
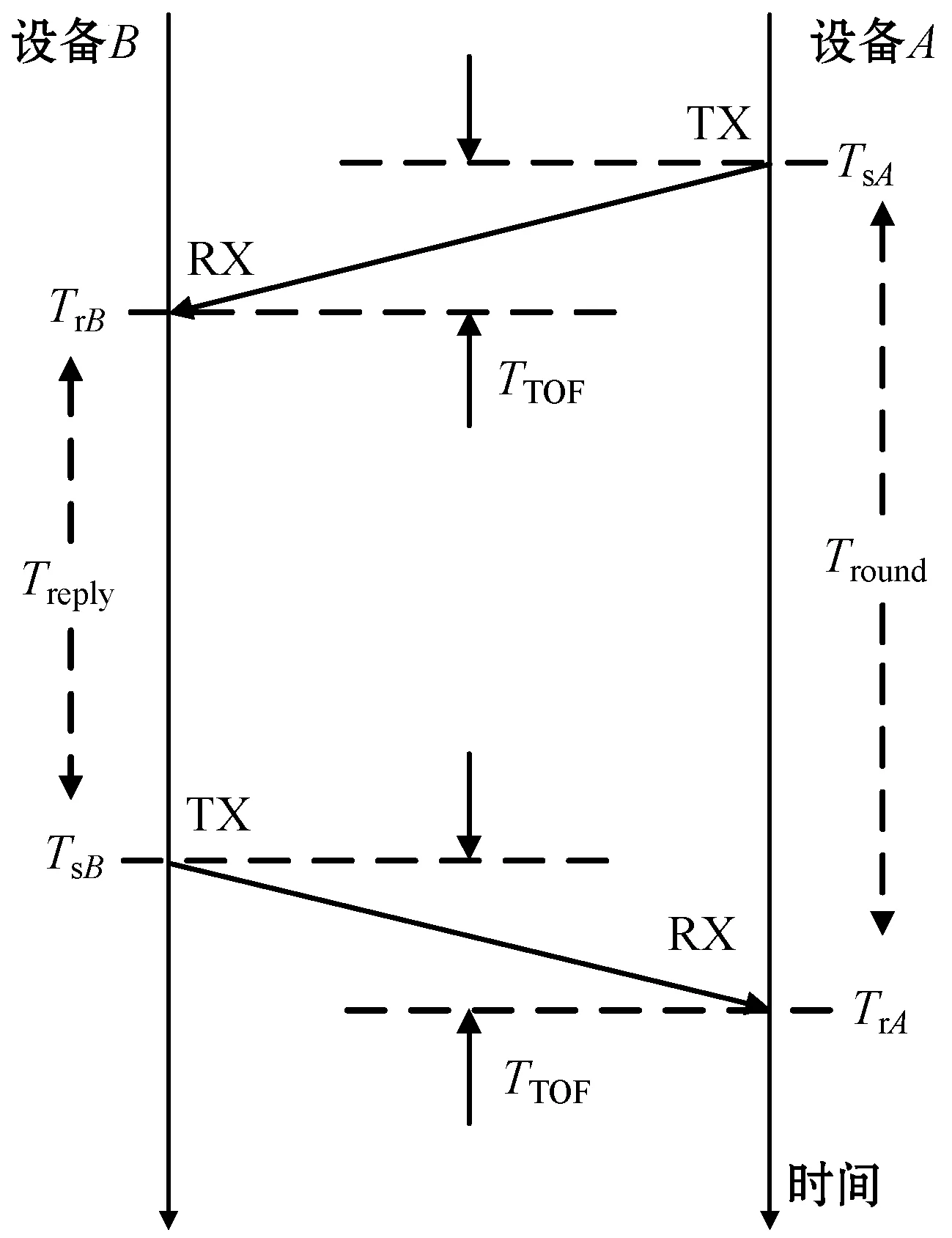
图1 TOF测距过程
(2)
2 系统设计与实现
如图2所示,系统由两部分组成:用于实现自动跟随的树莓派小车和跟随目标定位模块。跟随目标携带一块UWB主模块作为标签,小车配置两块UWB从模块作为基站。通过实时测量两个基站与标签之间的距离,结合数据处理来判断目标方向,实现跟随。

图2 系统硬件结构示意图
2.1 UWB模块选型
系统的UWB模块选用SWM1000射频模块。SWM1000模块是基于Decawave的DW1000收发器的集成电路,其集成了天线、电源管理和时钟电源系统,可用于高精度室内测距与定位。
2.2 跟随小车的结构设计
跟随小车由树莓派控制,小车的四个轮子各配有一个步进电机,树莓派通过驱动不同电机实现小车的前进、后退和转弯;通过控制PWM(Pulse Width Modulation)输出值的变化实现小车速度的变化。
作为基站的两块SWM1000从模块对称安装于小车后方左、右两端,与树莓派USB接口通过TTL转USB转换器相连。
2.3 跟随距离的确定
跟随目标上的标签与跟随小车上的两个基站绑定、配对后建立通信通道。单次测距由标签主动发起,基站一直处于等待监听状态,并在收到标签发来的测距开始消息后与标签交互完成一次距离测量[9]。获得与标签距离后,基站将测量距离通过USB接口发送至树莓派。
如图3所示,设定两个基站A、B各自与y轴的距离为常数ds。左侧基站A距离目标标签E长度为d1,右侧基站B距离目标标签E长度为d2,小车中心O距离目标标签E的距离为x,设目标标签E、小车中心O与x轴负方向构成夹角为θ。
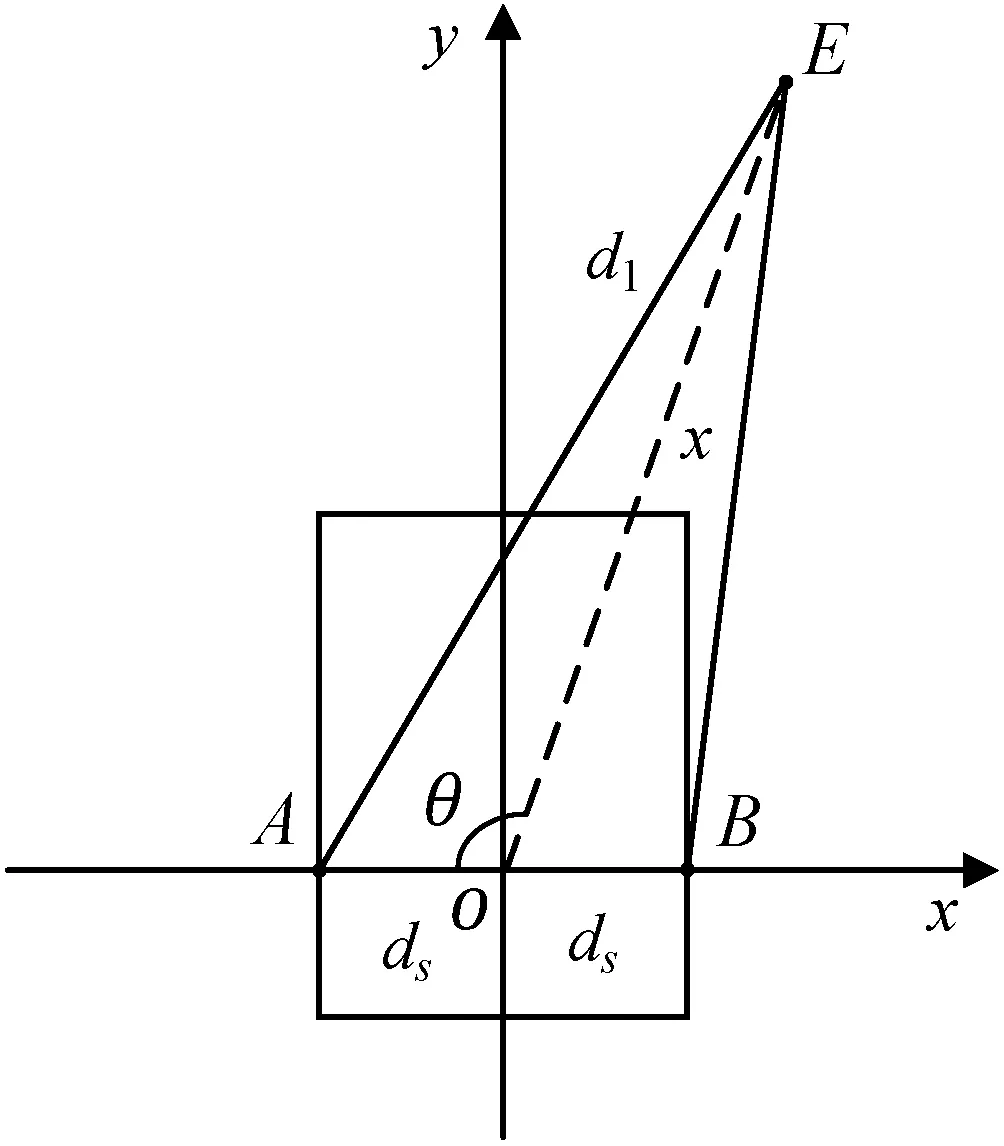
图3 跟随小车定位示意图
可以得到:
(3)
从而可以求解出未知量:
(4)
由此可见,小车与跟随目标的距离的计算仅与d1、d2和dS有关,与小车在当前距离下的具体朝向无关。
2.4 水平距离的计算
为了不影响跟随目标的正常移动,当跟随设备距离跟随目标一定距离时,跟随设备暂停接近,从而实现与目标保持距离的要求。这需要计算标签与跟随小车的水平距离。
跟随目标与跟随设备的距离如图4所示。设定小车左侧基站为A,右侧基站为B,基站A、B连线的中点为O,标签距离地面高度为DE=h。已知两个从模块至主模块的实时距离AE=d1,BE=d2,两基站至中点的距离AO=BO=dS。OE即式(4)所求x。

图4 基站与标签空间位置示意图
DE长度为标签距地高度,需要从外界获得,因为不同的高度会影响跟随设备与跟随目标水平距离OD的计算。
跟随设备距离目标的水平距离即为OD。易得:
x2=OD2+DE2
(5)
跟随小车与目标的水平停止距离可由外部输入设定,设该距离为k,即OD的理论最小值为k。小车实际运行时,只要在OD≤k的情况下,就会暂停进一步靠近,从而实现跟随小车实时与目标保持一定距离的要求。
3 跟随实现的误差讨论
3.1 理想状态的运动
在理想化的情况下,假设小车当前方向偏移其理想正对目标方向至多π/2,小车可以通过自身的左右旋转,以达到两基站测距值d1=d2,即达到两个基站与标签距离相等的方向。此时跟随小车正对目标,直行即可。若d1
3.2 实际状况的推导
在现实情况下,d1=d2的精准情况几乎难以稳定保持,因为小车直行时不能保证其没有任何角度的偏差,UWB在定位时也存在一定的误差[10]。因此,可以设定误差容忍区间,跟随小车的运动偏移情况只要在误差容忍区间内,就选择前进,如果超出,则在运动中纠偏,从而实现小车在运动过程中不断调整方向的需求。
如图4所示,令夹角α为小车理想正对目标方向与小车当前朝向所形成的夹角。为简化讨论,设定α∈[0,π/2],设D点的坐标为(xD,yD,0)。
通过空间解析几何分析,可以得到:
(6)
解得:
(7)
由式(7)可知,α的计算仅能确定小车当前车头方向相对于理想正对目标方向的偏移角度,但不能指出其具体偏移方向,即无法确定是左偏还是右偏。因此,需要同时结合d1和d2的大小关系判断小车具体的偏移方向。
在系统实际应用中,可设定小车距跟随目标任意距离处的误差容忍度数为γ。当α<γ,即小车运动偏移情况在误差容忍区间内,则直行;当α≥γ时,小车通过自身的偏移转动,调节车头方向,使α重新回归误差容忍区间内,实现运动中跟随。
因此,小车的运动逻辑如下:
由式(5)得,OD≤k时,小车暂停进一步靠近;当OD>k时,小车运动情况如表1所示。

表1 双基站定位跟随系统根据测距情况的运动调整逻辑表
综上所述,双基站定位跟随系统需要通过设定获得跟随设备与目标的水平停止距离k,标签距地高度h,误差容忍度数γ。在以上的条件下,跟随小车均能找到目标方向并进行调整,实现自动跟随的效果。
4 系统的优化方式
4.1 双基站定位跟随系统的缺陷与解决措施
3.2节的讨论均是以假设小车的理想正对目标方向与小车当前朝向偏差夹角至多π/2,即α∈[0,π/2]的情况为基础的。由此扩展到α∈[0,π],在这种情况下,小车可能处于相对于跟随目标的任意一种朝向。
当α∈(0,π/2)时,α的值即为式(7)所求解值。当α∈(π/2,π)时,通过空间解析几何分析:
(8)
在实际情况下,由于α∈[0,π],在一组确定的d1、d2情况下,计算过程中会出现小车正对目标和背对目标都有相应α解的问题,从而无法判断小车是否正向跟随目标。
如图5所示,取小车车头前进方向为y轴正方向,根据d1、d2求得的偏移角度可以是标签在E点时,利用式(7)计算出的偏移角α,也可以是标签在E′点时,利用式(8)计算出的偏移角α′。因此,小车是正对还是背对跟随目标无法通过d1、d2、dS的关系确定,也无法通过三者的关系确定选择使用式(7)还是式(8)的计算式来计算α。

图5 偏移角度α的多种取值情况
为了解决这个问题,可以定义β为小车理想正对目标方向与当前朝向所在的直线所成的非钝角,即β∈[0,π/2]。当α∈[0,π/2]时,β=α;α∈(π/2,π]时,β=π-α。因此,
(9)
β的计算式在α∈[0,π/2]与α∈(π/2,π]之间是统一的,其不受小车是否正对跟随目标而造成的计算影响。当获得一组d1、d2时,可通过式(9)直接计算出β的取值。
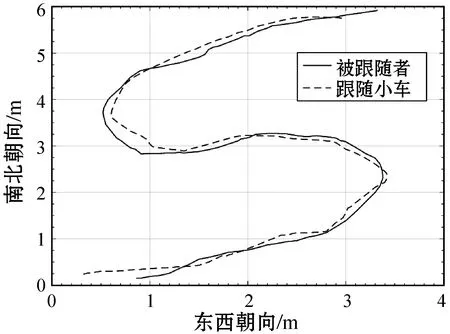
当d1>d2且β≥γ时,无论小车正对还是背对目标,都需要向左偏转;当d1 当β<γ时,如果仍参考表1的运动逻辑,那么跟随小车无论车头是正对还是背对跟随目标,均会执行向前运动的操作,从而可能出现直行背离跟随目标的情况。而只要始终保持该角度范围,这种背离会持续下去,形成“完美背离”现象。 对于这种情况,可以先让小车直行运动,计算一段时间内的x累计变化。如果该段时间内x的值是持续变大的,则判断为小车正在背离运行目标,因此需要调转车头;相反,如果x的值在直行过程中是逐渐变小的,则可以判断小车正在接近目标,方向是正确的。 修正后的运动逻辑如下: 当x≤k时,小车暂停进一步靠近;当x>k时,小车运动情况如表2所示。 表2 修正后双基站定位跟随系统的运动调整逻辑表 4.1节中的方法虽然可以解决问题,但是如果在计算累计变化的过程中,跟随目标做出的是变速幅度较大的移动,跟随小车就容易出现判断错误。同时,双基站定位系统依赖于用户自行输入的标签高度。一方面,这需要保证系统的高度设置要跟随标签的高度变化而进行修改。另一方面,如果标签高度的输入出现误差,会影响跟随小车到目标的水平距离计算,导致系统跟随效果变差。 为解决这些问题,可以引入第三个基站,构建三基站定位系统。第三个基站安装于小车的头部,三个基站构成一个等边三角形。 如图6所示建立坐标系,A、B、C为三个基站,三角形ABC为等边三角形。E为标签,标签E投影至xoy平面于D。AB=AC=BC=2dS,H是等边三角形ABC的中心。O为AB中点。设定A基站、B基站、C基站与标签的距离分别为d1、d2、d3。设小车理想正对目标方向与小车当前朝向所形成的夹角,即图中DH与y轴正方向所成角为α(α∈[0,π])。 图6 三基站定位示意图 令E点坐标为(xE,yE,zE),通过空间解析几何求解,可以得到: (10) 解得: (11) α=∠DHC= (12) 由式(11)可以得到,DH的长度与ED无关,即标签E的高度对DH的计算没有影响,所以三基站定位跟随系统不需要外部输入标签高度。 之所以在双基站定位跟随系统中出现“完美背离”的情况,是因为系统仅通过d1和d2的关系,无法区分跟随小车正对或背对目标的状态。而三基站系统中α∈[0,π],只要获得一组d1、d2、d3的值,就可以通过式(12)计算出α的值,从而明确地判断小车相对目标方向的具体偏移度数。 仍设定跟随小车与目标的水平停止距离为k;跟随小车距标签任意距离处,误差容忍度数为γ。三基站定位跟随系统中小车运动逻辑如下: 由式(11)得,DH≤k时,小车暂停进一步靠近;当DH>k时,小车运动情况如表3所示。 表3 三基站定位跟随系统根据测距情况的运动调整逻辑表 综上所述,三基站定位跟随系统只需设定跟随小车与目标的水平停止距离k,误差容忍度数γ,即可实现小车的自动跟随。其不仅减少输入参数的个数,同时解决双基站定位系统中“完美背离”的情况,更易处理分析。 实验进行于东西朝向4 m,南北朝向6 m的房间内部。被跟随者与小车各自额外携带一块UWB定位标签,房间四个角落分别安装一块UWB定位基站。通过四个定位基站对两个定位标签测距即可计算出被跟随者与小车位于室内的坐标。 被跟随者采用正常步速运动。设定双基站定位跟随系统最小保持距离k=0.4 m,标签距地高度h=1.5 m,最大误差容忍度数γ=π/6。其运动路径与双基站定位跟随小车运动路径如图7所示。 图7 双基站定位跟随中被跟随者与跟随小车运动路径 设定三基站定位跟随系统最小保持距离k=0.4 m,最大误差容忍度数γ=π/6,无须设定标签距地高度。被跟随者与三基站定位跟随小车的运动路径如图8所示。 图8 三基站定位跟随中被跟随者与跟随小车运动路径 可见,无论是双基站定位还是三基站定位,均可实现小车的室内自动跟随,识别准确,不易跟丢。三基站相较双基站定位跟随方法,在保证准确跟随的同时,减少参数的输入,并避免“完美背离”的发生。 本文以UWB定位为基础,提出可以实时路径纠偏,实现智能跟随的自动跟随设备。由跟随过程中的误差讨论,提出并改进双基站跟随小车的跟随方式,并进一步提出三基站定位跟随的优化方法。在实验过程中,跟随小车已成功实现智能定位和跟随。本系统具有识别准确度高、跟随中纠偏等多种优势,具有良好的应用价值。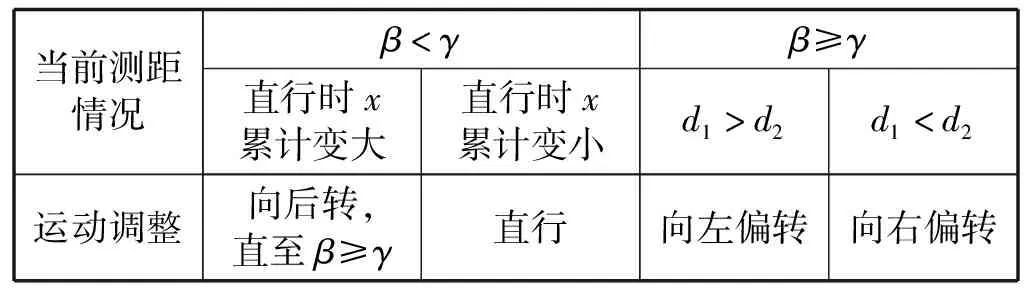
4.2 三基站定位跟随的优化与实现


5 实验数据与分析

6 结 语

