政府补贴下E-闭环供应链定价及回收服务决策

白世贞 张雪莲 姜 曼 陈化飞

(哈尔滨商业大学管理学院 黑龙江 哈尔滨 150028)

0 引 言

随着资源浪费和环境污染问题的日趋严峻，废弃电器电子产品的回收处理与再生利用现已成为社会各界普遍关注的焦点。如今，越来越多的电器电子产品制造商利用官方商城进行线上直销的同时，还设立了“以旧换新”服务专区，与网络回收平台达成服务合作，共同从事线上回收业务，最终形成E-闭环供应链。在回收环节，网络回收平台除自营回收外，也为制造商提供代理回收服务，并将废弃电器电子产品回收信息整合后传递给制造商。顾客从制造商和网络回收平台双回收渠道中享受的回收服务水平是一致的，但在不同回收渠道获得的回收价格不同，从而产生渠道竞争。为了促进资源高效循环利用以及加大环境保护力度，国内已先后颁布了多种相关政策法规。其中《废弃电器电子产品处理基金征收使用管理办法》提出要鼓励生产者自行回收处理废弃电器电子产品，并提出要根据实际拆解处理的废弃电器电子产品数量，对处理商给予定额补贴[1]。由于影响消费者主动参与废弃电器电子产品回收的因素中，经济动机与服务动机所占权重相对较大[2-3]，说明E-闭环供应链中各企业亟须决策更优的价格及回收服务水平以吸引消费者参与回收，而政府颁布的补贴政策必然会对企业决策产生影响。因此，E-闭环供应链中各企业在政府补贴政策下如何作出相应决策将是一个非常值得探讨的问题。

关于闭环供应链的定价决策问题，郑本荣等[4]建立第三方负责再制造的闭环供应链，探讨了专利许可情况下的最优决策问题。丁斌等[5]在供应商参与和不参与回收再制造情况下，对比分析了两种闭环供应链模型的定价决策及收益。郭金森等[6]探讨了包括零售商负责回收再制造在内的三种再制造模式下闭环供应链的最优定价决策问题。上述文献分别考虑了供应商、零售商或第三方负责再制造的情形。在制造商负责再制造的情况下，Huang等[7]研究了具有双回收渠道的闭环供应链最优决策问题。Saha等[8]在奖励驱动政策下，探讨了闭环供应链的最优决策与协调问题。Zheng等[9]在研究闭环供应链定价决策时考虑了渠道竞争和权力结构的作用。在定价决策基础上，不少学者还考虑了服务水平的决策，Zhang等[10]对客户忠诚度如何影响闭环供应链的定价及零售服务水平决策进行了分析。Wu[11]研究了由两个制造商和一个共同零售商组成的闭环供应链的最优价格及服务水平决策问题。另外，对于闭环供应链中回收渠道竞争的研究同样也是学者们关注的焦点。倪明等[12]探讨了回收渠道竞争对三种双回收渠道模式下最优决策的影响情况。郑本荣等[13]分析了制造商和第三方回收商之间的渠道竞争对制造商最优联盟结构选择的影响。Wang等[14]在考虑信息不对称情况下，探讨了回收渠道竞争对闭环供应链最优定价决策的作用情况。由于政府补贴政策在引导废旧品循环利用方面发挥着积极作用，因此学者们对作用于闭环供应链的政府补贴政策也进行了分析。赵敬华等[15]对不同补贴对象如何影响闭环供应链各成员定价策略和收益进行了研究。彭志强等[16]基于政府分别对制造商和零售商实施补贴两种形式，研究了闭环供应链的最优决策问题。程发新等[17]分析了政府补贴对考虑回收质量不确定的闭环供应链最优决策的影响。

信息技术的飞速发展给供应链的销售和回收环节均带来巨大的影响。众多国内外学者愈加关注由线上销售与线上回收构成的E-闭环供应链。在E-供应链方面，Siddiqui等[18]利用五维框架结构对E-供应链体系进行分析，发现前期注重创新和发展，后期则转移到供应链整合和协作方面。而当E-供应链发展趋向成熟时，越来越多的制造商利用网络平台进行线上销售的同时，还对废旧品回收信息进行采集和整理，从而形成E-闭环供应链体系[19]。关于线上回收，王玉燕等[19]建立了由制造商和负责发布销售及回收信息的网络平台组成的E-闭环供应链结构，求解出最优价格及服务水平决策；朱晓东等[20]将线上回收商考虑到闭环供应链结构中并求出最优定价决策；Feng等[21]考虑传统回收和网络回收两种模式，分析了相关参数对回收渠道选择的影响。

可见，多数学者主要还是围绕闭环供应链以及政府补贴对闭环供应链的影响展开研究，虽有部分学者考虑了线上回收渠道，但较少对线上销售与回收结合形成的E-闭环供应链结构展开研究，也未考虑政府补贴政策对E-闭环供应链决策的影响。鉴于此，本文构建有、无政府补贴的E-闭环供应链决策模型，求解两种模型下的博弈均衡解，分析政府补贴对回收价格、回收服务水平、回收量和利润的影响，并探讨回收服务水平敏感系数对各均衡解的作用情况，最后为带动E-闭环供应链各企业积极参与回收提出有效建议。

1 模型介绍

1.1 问题描述

考虑E-闭环供应链是由单个制造商和单个网络回收平台组成。制造商一方面利用新材料和从废弃电器电子产品中提取的可再利用材料生产产品，并通过线上渠道直销给顾客；另一方面，与网络回收平台进行回收服务合作，共同从事线上回收业务。在回收环节，制造商委托网络回收平台代理提供回收服务，并支付一定数量的佣金额作为其报酬。网络回收平台除为制造商代理提供回收服务外，同时也自营回收业务，回收来的废旧品因仍具有剩余价值，可通过二次销售获得相应收益。对顾客来说，从制造商和网络回收平台双回收渠道中享受的回收服务相同，但获得的回收价格存在区别，因此回收渠道之间存在竞争。此外，制造商由于负责拆解废弃电器电子产品，并将可利用材料用于再制造，因此可以根据其拆解数量获得政府给予的定额补贴。本文考虑两种E-闭环供应链结构：无政府补贴下和有政府补贴下双回收渠道E-闭环供应链结构，分别如图1(a)和图1(b)所示。

(a)无政府补贴下

1.2 符号说明

Pn表示新产品单位销售价格。

Pm表示制造商单位回收价格。

Pt表示网络回收平台单位回收价格。

s表示网络回收平台为消费者提供的回收服务水平，定义回收服务成本为s2/2。实践中，网络回收平台可以为顾客提供邮寄、当面交易(上门回收/地铁站回收)、数据清除、专业质量检测和信息咨询等服务。

cn、cr分别表示制造商利用新材料或拆解处理后提取的可再利用材料进行生产的成本。由于再制造存在成本优势，满足Δ=cn-cr>0。

λ表示制造商为网络回收平台代理提供的回收服务支付的单位固定佣金额。

g表示政府为制造商的拆解处理提供的单位固定补贴额。

v表示网络回收平台通过二次销售等处理途径获得的单位收益。

D表示市场需求函数，其与销售价格Pn呈负相关关系，设D=φ-Pn，φ表示潜在的最大可能市场需求量。

Qm、Qt分别表示制造商和网络回收平台的回收函数，主要与回收价格和回收服务水平相关。本文构建的双回收渠道中，制造商和网络回收平台的回收服务均由网络回收平台提供，回收服务水平相同，但回收价格因二者分别决策而存在区别。结合双回收渠道闭环供应链中回收函数设计的特点[22]，参考文献[23]设计的同时考虑销售价格和销售服务水平的市场需求函数，并为简化模型，设计本文的废旧品回收函数为：

制造商的回收函数：

Qm=Pm-αPt+βs

(1)

网络回收平台的回收函数：

Qt=Pt-αPm+βs

(2)

式中：α为制造商与网络回收平台之间的回收价格竞争系数，0<α<1；β为顾客对回收服务水平的敏感度，0<β<1。

上标“Y”与“N”分别代表有、无政府补贴的E-闭环供应链模型；上标加入“*”表示最优决策结果。

1.3 基本假设

假设1制造商和网络回收平台之间存在斯坦伯格博弈关系，其中，制造商为博弈领导者，网络回收平台为追随者。

假设2制造商和网络回收平台之间的信息是完全对称的，且二者均是风险中性和完全理性的。

假设3制造商分别利用新材料和拆解提取的再利用材料生产的新产品和再造品在质量、外观和价格上均无区别，并且顾客对两者的接受度完全相同。

假设4制造商回收来的每单位废旧品经过加工均可成为再造品。

假设5本文只考虑单周期情况，即假设市场前期就已存在销售出去的产品，因此当前的周期可直接回收废旧品。

2 不同模式E-闭环供应链决策模型

2.1 无政府补贴的E-闭环供应链决策模型

(3)

(4)

系统总利润函数ΠN为：

(5)

命题1无政府补贴的E-闭环供应链中，当2-α2-β2-αβ2>0时，制造商的利润函数存在唯一最优解。制造商和网络回收平台的最优决策分别如下：

产品最优销售价格：

(6)

制造商最优回收价格：

(7)

网络回收平台最优回收价格：

(8)

网络回收平台最优回收服务水平：

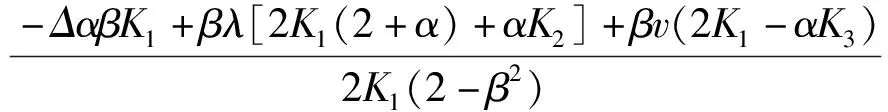
(9)

产品最优需求量：

(10)

制造商最优回收量：

(11)

网络回收平台最优回收量：

(12)

制造商最优利润：

(13)

网络回收平台最优利润：

2λK1(α+β2)+αλK2]/[2K1(2-β2)]}·

{[-ΔαK1+v(K1+K5)+λ(αK2-2K1K3)]/

[2K1(2-β2)]}+λ·[ΔK1+λK4(1+α)-vK3]/

αβλK2+βv(2K1-αK3)]/[2K1(2-β2)]}2

(14)

系统最优总利润：

ΠN*=(φ-cn)2/4+[Δ-(ΔK1-λK2+vK3)/(2K1)]·

[ΔK1+λK4(1+α)-vK3]/[2(2-β2)]+

{2vK1(2-β2)-ΔαK1-v[2K1(1-β2)+αK3]+

λ[2K1(α+β2)+αK2]}/[2K1(2-β2)]·

{[-ΔαK1+v(K1+K5)+λ(αK2-2K1K3)]/

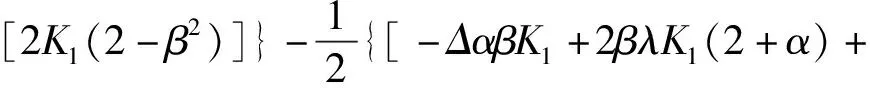
αβλK2+βv(2K1-αK3)]/[2K1(2-β2)]}2

(15)

证毕。

2.2 有政府补贴的E-闭环供应链决策模型

(16)

(17)

系统总利润函数ΠY为：

(18)

命题2有政府补贴的E-闭环供应链中，当2-α2-β2-αβ2>0时，制造商的利润函数存在唯一最优解。制造商和网络回收平台的最优决策分别如下：

产品最优销售价格：

(19)

制造商最优回收价格：

(20)

网络回收平台最优回收价格：

λ[2K1(α+β2)+αK2]}/[2K1(2-β2)]

(21)

网络回收平台最优回收服务水平：

sY*={-αβ(Δ+g)K1+βλ[2K1(2+α)+αK2]+

βv(2K1-αK3)}/[2K1(2-β2)]

(22)

产品最优需求量：

(23)

制造商最优回收量：

(24)

网络回收平台最优回收量：

(25)

制造商最优利润：

(26)

网络回收平台最优利润：

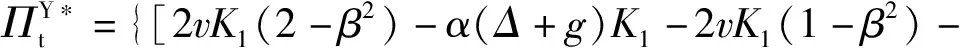
αvK3+2λK1(α+β2)+αλK2]/[2K1(2-β2)]}·

{[-α(Δ+g)K1+v(K1+K5)+λ(αK2-2K1K3)]/

[2K1(2-β2)]}+λ·[(Δ+g)K1+λK4(1+α)-

2βλK1(2+α)+αβλK2+βv(2K1-αK3)]/

[2K1(2-β2)]}2

(27)

系统最优总利润：

ΠY*={[2vK1(2-β2)-(Δ+g)αK1-2vK1(1-β2)-

αvK3+2λK1(α+β2)+αλK2]/[2K1(2-β2)]}·

{[-(Δ+g)αK1+v(K1+K5)+λ(αK2-

[Δ+g-(ΔK1+gK1-λK2+vK3)/(2K1)]·

{[(Δ+g)K1+λK4(1+α)-vK3]/[2(2-

αβλK2+βv(2K1-αK3)]/[2K1(2-β2)]}2

(28)

证毕。

3 比较分析

结论1通过比较有、无政府补贴时的销售价格、需求量、回收价格、回收服务水平和回收量，得如下关系：

证毕。

结论1表明，有政府补贴相较于无政府补贴的情形下：① 对制造商而言，正向销售环节的产品销售价格和市场需求量未发生变化，而逆向回收环节的废旧品回收价格和回收量均提高。② 对网络回收平台而言，废旧品回收价格提高，但回收服务水平和回收量均降低。这表明政府补贴对制造商的销售业务并未产生影响，但对制造商和网络回收平台的回收业务发挥了作用。在政府补贴作用下，制造商提高了废旧品的回收价格，并相应的提高了回收量；网络回收平台为吸引顾客，也提高了回收价格，但同时降低了其提供的回收服务水平，此时网络回收平台的回收量减少。可见，政府补贴的存在有效推动了制造商的回收处理活动，但同时损害了网络回收平台的回收业务。接下来，继续将政府补贴对系统总回收量的影响情况进行分析。

证明：通过对有、无政府补贴的系统总回收量作差可得：

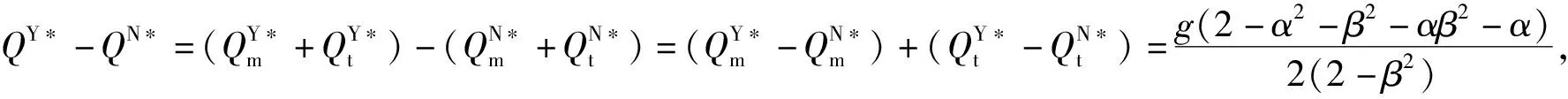
证毕。

结论3通过比较有、无政府补贴时的制造商和网络回收平台最优利润，得如下关系：

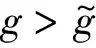
证毕。

由结论1至结论3可知，政府补贴的实施有利于提高制造商的回收价格、回收量及利润，鼓励制造商积极参与回收处理。但由上述结论可知，政府补贴的存在降低了网络回收平台的回收量，且当补贴额度较小时，甚至可能损害网络回收平台的利润。另外，政府补贴对系统总回收量的影响要受到顾客对回收服务水平敏感度的作用。因此，为鼓励网络回收平台积极参与回收，现提出以下建议：① 政府需根据现实情况调控给予制造商的固定补贴额，从而实现制造商和网络回收平台利润均提高的双重目标。② 制造商应提高支付给网络回收平台的佣金额，增加网络回收平台的收益，从而推动网络回收平台不断提升回收服务水平。③ 作为专门从事废弃电器电子产品线上回收业务的网络回收平台，其利润来源相对制造商来说还比较少，政府层面除为制造商提供拆解处理补贴外，还应为网络回收平台提供一些扶持性政策，从而鼓励网络回收平台积极参与回收。

4 算例分析

本节将利用MATLAB软件进行算例分析，进一步探讨政府补贴参数和回收服务水平敏感系数的变化对各决策变量的影响情况。对模型参数赋值：φ=200，α=0.6，cn=50，Δ=20，v=5，λ=2。

4.1 政府补贴的影响

固定β=0.8，取g∈(0,12)，研究政府补贴参数对回收价格、回收服务水平、回收量和利润的影响情况，具体如图2-图4所示。

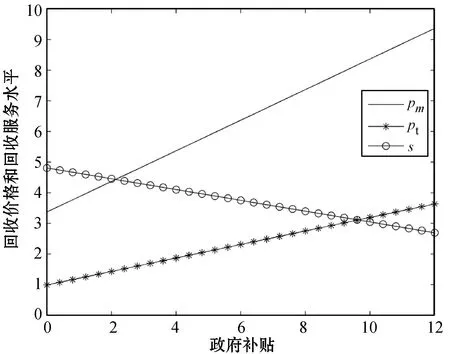
图2 回收价格、回收服务水平随政府补贴的影响

图3 回收量随政府补贴的影响

(a) (b)

由图2可以看出，随着政府补贴的增加，制造商和网络回收平台的回收价格逐渐增加，而网络回收平台的回收服务水平逐渐减少。另外，制造商回收价格的增加幅度要比网络回收平台回收价格的增加幅度更大，说明政府补贴对制造商回收价格的作用强度要高于对网络回收平台回收价格的作用强度。由图3可以看出，随着政府补贴的增加，制造商的回收量逐渐增加，而网络回收平台的回收量逐渐减少。这说明，政府补贴的增加可有效鼓励制造商积极参与废弃电器电子产品的回收处理，此时的制造商会主动提高回收价格，加大回收力度，从而增加回收量。由于制造商和网络回收平台之间存在竞争关系，因此，网络回收平台为吸引顾客参与回收，应对来自制造商的回收竞争，也选择提高回收价格，但会通过降低回收服务水平来减少成本支出。当政府对制造商实施补贴政策时，制造商回收价格的增加幅度要明显高于网络回收平台的增加幅度，从而损害了网络回收平台的回收业务。由图4可以看出，制造商利润随着政府补贴的增加而增加，网络回收平台利润随着政府补贴的增加表现为先减少后增加的趋势。这说明，政府补贴的增加恒有利于提高制造商利润，从而有效带动制造商参与废弃电器电子产品回收处理的主动性与积极性。而对于网络回收平台而言，当政府补贴g∈(0,go)时，网络回收平台的回收业务由于制造商回收量的增加而受到损害，导致利润逐渐减少；当政府补贴g∈(go,12)时，较高的政府补贴使得制造商回收量得到大幅度提高，此时网络回收平台的回收业务虽仍然受损，但来自制造商的佣金收入弥补了这部分损失，使得网络回收平台利润逐渐提高。可见，只有合理设置补贴额度才能实现制造商和网络回收平台利润均提高的双重目标。因此，我国政府为加快废弃电器电子产品回收处理行业的发展，需根据现实情况调控给予制造商的固定补贴额度，实现制造商和网络回收平台共同受益，从而有效带动二者参与回收处理业务的主动性与积极性。

4.2 回收服务水平敏感系数的影响

固定g=5，取β∈(0.70,0.85)，分析回收服务水平敏感系数对E-闭环供应链回收价格、回收服务水平、回收量和利润的影响情况，如图5-图7所示。

图5 回收价格和回收服务水平随回收价格敏感系数的影响

图6 回收量随回收服务水平敏感系数的影响

图7 利润随回收服务水平敏感系数的影响

由图5可见，随着回收服务水平敏感系数的增加，网络回收平台的回收服务水平逐渐增加，而制造商和网络回收平台的回收价格均逐渐减小。这表明，回收服务水平敏感系数越高，顾客对回收环节享受的回收服务水平越敏感，因此网络回收平台提升提供给消费者的回收服务水平，从而改善消费者回收体验，同时制造商和网络回收平台降低支付给消费者的回收价格以减少回收环节产生的成本。由图6可见，随着回收服务水平敏感系数的增加，制造商的回收量逐渐减少，网络回收平台的回收量逐渐增加。这说明，当回收服务水平敏感系数增加时，即顾客对回收服务水平的敏感程度逐渐提高，导致制造商的回收量降低，网络回收平台的回收量提高。因此，制造商为加大回收力度，应提高回收价格，而为弥补制造商高价回收的利润损失，此时则需要得到政府大力支持，这更加强调了加大政府补贴额度的重要性。由图7可见，制造商利润随回收服务水平敏感系数的增加呈现了逐渐上升的趋势，网络回收平台利润随回收服务水平敏感系数的增加呈现了先降低后上升的趋势。这说明，随着顾客对回收服务水平敏感程度的逐渐提高，制造商总是不断获利，而网络回收平台的利润在一定范围内是受损的。

5 结 语

本文讨论了有、无政府补贴下由制造商和网络回收平台共同回收组成的双渠道E-闭环供应链最优决策问题。政府补贴对回收价格、回收服务水平、回收量和利润均产生不同程度的影响。若回收服务水平敏感系数较高，有政府补贴时的总回收量相较于无政府补贴时减少。政府补贴始终有利于提高制造商利润，只有合理地设置政府补贴，才能提高网络回收平台利润。随着回收服务水平敏感系数的增加，制造商利润总是提高，而网络回收平台利润在一定范围内降低。鉴于此，现提出如下建议：① 政府需及时调控补贴额度，既促使制造商提高回收价，又提高网络回收平台利润，从而实现经济效益与社会效益双赢。② 制造商应提高支付给网络回收平台的佣金额，推动网络回收平台不断提升回收服务水平。③ 政府在为制造商提供补贴基础上，还应为网络回收平台提供若干扶持性政策，从而鼓励网络回收平台积极参与回收，支持互联网回收模式发展。政府除为制造商提供补贴外，也会向其征收处理基金，未来可将基金征收政策也考虑到模型中，这将是另一个值得研究的问题。