坝基岩体裂隙渗流效应数值模拟方法

蒋中明肖喆臻唐 栋

（1. 长沙理工大学 水利工程学院，湖南 长沙 410114；2. 长沙理工大学 水沙科学与水灾害防治湖南省重点实验室，湖南 长沙 410114；3. 长沙理工大学 洞庭湖水环境治理与生态修复湖南省重点实验室， 湖南 长沙 410114）

1 研究背景

1959年法国67 m高的Mal-passet薄拱坝与1963年意大利265 m高的Vajiont拱坝[1]均因忽视岩体中水的渗流效应影响而引发了严重后果。在此之后，渗流效应对大坝坝基、地下洞室以及边坡等工程安全性的影响逐渐为大家所重视。为了分析岩体渗流对工程安全性的影响，众多学者提出并发展了等效连续介质模型、离散裂隙网络模型和双重介质模型等裂隙岩体渗流模型。

等效连续介质模型简单、理论完善，由Snow[2]提出，并由Oda、Neuman和Depner等学者[3-5]逐渐完善。该方法适合于裂隙密集的工程岩体渗流问题分析。但是对于裂隙稀疏，或岩体渗透性样本单元体积REV不存在的情况，等效连续介质模型并不适用；周志芳等[6]研究了优势裂隙对渗流的影响，谭春等[7]提出使用灰色理论确定岩体表征单元体。此外，等效连续介质模型只能大概反映区域流量的变化，并不能真实反映裂隙水的渗流路径和小于REV区域渗流场的分布情况。

离散裂隙网络模型假定渗流只发生在裂隙中，忽略了孔隙渗流。离散裂隙网络模型由于忽略了岩块的孔隙渗流，所以不适用于岩块基质渗透性较大的情况。另外，现阶段三维裂隙网络渗流的求解难度大，耗时长，对解决工程尺度渗流问题仍有相当难度。裂隙渗流的求解方法也多种多样，例如Dverstorp[8]假定岩体中渗流路径是在裂隙中光滑的管道中进行。N.Koudina[9]、李新强[10]则基于边界元法求解三维多边形裂隙网络渗流问题。何忱等[11]将岩石看作由不透水的四面体块体组成的集合，渗流只在相邻块体之间的界面上发生，用界面网络代替了岩石的孔隙结构，裂隙也以界面形式显式存在于岩体之中，并遵循Darcy定理。李海枫等[12]也采用Delaunay三角剖分技术生成离散裂隙网络模型以研究裂隙岩体非饱和渗流问题。

双重介质模型最初由Barenblatt等[13]提出，是另一种等效连续体模型。其基本思路是将孔隙介质的连续体单元和裂隙网络的离散裂隙视为同一空间内可以相互交换流体的连续体。Aifantis[14]基于混合物理论提出并推导了流固耦合方程，但是其部分方程是基于物理意义得出而非数学推导。由于双重介质模型没有从正面考虑离散裂隙与单元之间的连接问题，所以导致节点上出现两个水头的情况，高海鹰和吴宏明[15]通过假设裂隙与单元相交的面水头相同、流量不连续建立了混合模型，并对裂隙与单元连接处做了讨论。黎水泉等[16]经过数学推导，得到了双重介质模型的流固耦合方程。

为了综合利用等效连续介质模型和离散裂隙网络模型二者各自的优点，侯晓萍和徐青等[17]采用复合单元法研究了裂隙岩体非稳定渗流分析方法，其主要思路是将处于连续介质单元内部的离散裂隙通过拓扑计算，在单元内部形成基于裂隙面的若干子单元，并通过建立平衡方程后统一求解；该方法对于密集裂隙情况下的渗流计算仍需要进行发展。王臻等[18]用Oda的裂隙张量理论来获得子区域的渗透张量，然后采用DC模型（离散连续模型）分析二维渗流问题，取得了良好效果。近年来，国外部分学者提出了EFC模型（Embedded Fractured Continuum）[19-22]，即在连续介质单元中考虑了裂隙影响来模拟裂隙岩体的渗流效应。以上方法在本质上还是属于连续介质渗流的分析方法。本文在上述方法的基础上，通过对岩体中裂隙渗流特性分析，将单元中的裂隙渗透性按各向异性处理，并将之与块体渗透性进行叠加，从而实现用连续介质模型模拟岩体裂隙渗流效应的数值计算方法。

2 裂隙介质EFE渗流模型

嵌入裂隙单元（Embedded Fractured Element）的渗透性由单元中的裂隙数量、各裂隙开度以及裂隙周围的岩块渗透性共同确定。对大多数岩体而言，由于岩块的渗透性相对较小，故其渗透性往往由岩体中包含的裂隙数量及其几何和充填特征所控制。图1所示的六面体单元中包含了2条水平贯通裂隙和1条铅直贯通裂隙。如果岩块和裂隙渗透性分别用Kr和Kf表示，单元在3个方向上的渗透系数分别用kxx、kyy和kzz表示，对于裂隙岩体，大多数情况下都满足Kr ＜＜Kf条件，因此单元渗透性主要由Kf贡献。具体地说，图1中的单元在z方向上的渗透性主要由f3控制；单元在x方向上的渗透性由f1和f2共同决定；单元在y方向上的渗透性则受到f1、f2和f3共同影响。假定图1中的各裂隙开度相同，则存在kxx =2 kzz和kyy =3 kzz关系。这表明裂隙的存在使得单元呈现出了显著各向异性特点。含裂隙单元渗透性的各向异性特性可以采用各向异性连续介质渗流模型来刻画。

图1 裂隙单元示意

大量试验研究表明，对于不可压缩流体，岩块（孔隙介质）中流体运动服从达西定律[23]。当缝宽较小，且水流流态为层流时，流体沿裂隙面流动也服从达西定律。所以对于岩体来说在恒定流情况下，渗流方向上的总流量Q由裂隙流量Qf和岩块流量Qr组成：

式中：Q为渗流方向上的总流量；Qf为渗流方向上岩体裂隙的流量；Qr为渗流方向上岩体岩块的流量。于是在水力梯度相同的情况下，可得整体等效渗透系数张量Kij为：

式中：A为渗流方向截面面积；Ar为渗流方向岩块所占面积；Af为渗流方向裂隙横截面面积；Kr为岩块渗透系数；Kfij为裂隙渗透系数。由于裂隙开度很小，一般情况下，存在以下关系：

于是式（2）可改写为：

式中：Lfi为单位面积上第i条裂隙的迹长；bi为第i条裂隙的开度；nf为渗流方向面积裂隙率，其中角度θ为裂隙面与渗流方向横截面的夹角。

当计算单元中没有包含裂隙时，由式（6）可知计算单元渗透系数Kij =Kr，计算域内岩体渗透性完全可以用孔隙连续介质来描述。孔隙连续介质可以各向同性材料，也可以是各向异性材料。工程分析时，由于计算单元的尺度远远大于单元内的空隙尺度，因此绝大多数情况下采用各向同性的假定是合理的。

当计算单元中包含裂隙时，单元渗透系数由Kr和Kf,ij共同决定。当计算单元尺度大，包含裂隙数量少时，尽管Kf,ij一般相对较大，但由于式（6）中的nf相对较小，单元渗透性可能主要由岩块渗透性决定；反之，当计算单元尺度较小，nf相对较大，故单元渗透性主要由裂隙渗透性决定。

由于Kf,ij具有显著的各向异性特点，因此计算域内岩体的渗透性必然也将呈现出显著各向异性特点，即含裂隙单元为完全各向异性材料。渗透张量可通过立方定律确定。采用Snow[2]的假设，即使不同方向裂隙组在裂隙网络系统中相互连通，不同方向裂隙组内的裂隙水流互不干扰，且裂隙贯穿整个单元，单元各个方向上的流量等于各裂隙在相应方向上的流量和，即流量满足叠加原理。于是，渗透张量Kf,ij的矩阵表达式如下[2]：

式中：Kf,ij为单元中包含的裂隙对计算单元渗透张量的贡献；m为裂隙个数；g为重力加速度；b为裂隙开度；υ为流体运动黏滞系数；αxi、αyi、αzi为第i个裂隙面单位法向向量在3个方向上的分量，可由裂隙面的倾向及倾角求出。

由此可见，式（6）既适用于单元中有裂隙的情况，也适用于单元中无裂隙分布情况。因此，采用式（6）对计算域内不同部位的岩体分别采用不同属性的渗透系数就可以真实地反映岩体中的裂隙渗流效应（图2中的裂隙等效单元，即EFE单元）以及块体内的孔隙渗流效应（图2中的基质单元）。由于裂隙面宽度都很小，为了尽可能降低裂隙等效单元尺度过大对裂隙附近范围的渗流形态的影响，可以采用如图2中的网格加密技术对裂隙穿过的单元进行网格加密，从而减少裂隙渗流单元的数量。

图2 裂隙岩体网格剖分

3 EFE渗流模型的数值实现

对于工程尺度的渗流分析来说，采用完全连续孔隙介质模型或完全离散裂隙网络模型都是不可接受的。在实际工程中，岩体中分布的裂隙尺度大小不均，如果全部纳入到离散裂隙网络模型中，其计算工作量将是不可接受的。

一种可行的方案是将一些小尺度的裂隙空间纳入到孔隙空间范围，并将其按孔隙介质渗流（基质单元/孔隙单元）进行处理，而尺度大的裂隙及结构面等按等效裂隙渗流单元（EFE）进行处理是合理的。式（6）刚好具备同时描述裂隙渗流特性和孔隙渗流特性的能力。

利用式（6）对分析域同时进行裂隙渗流特性和孔隙渗流特性分析的前提是计算软件需要同时具备三维裂隙网络生成及处理能力以及连续介质渗流分析能力。在计算过程中，对所有单元根据试验值综合确定其渗透系数。对存在裂隙的单元，根据裂隙的分布情况利用式（8）自动计算其各向异性渗透系数，并对计算单元渗透系数进行修正；对于不包括贯通裂隙的单元，则不需进行渗透性修正。由此可见，上述利用裂隙等效单元获取裂隙渗流效应的方法只需在原有的渗流分析程序中添加包含裂隙的单元渗透系数处理模块就可以实现。

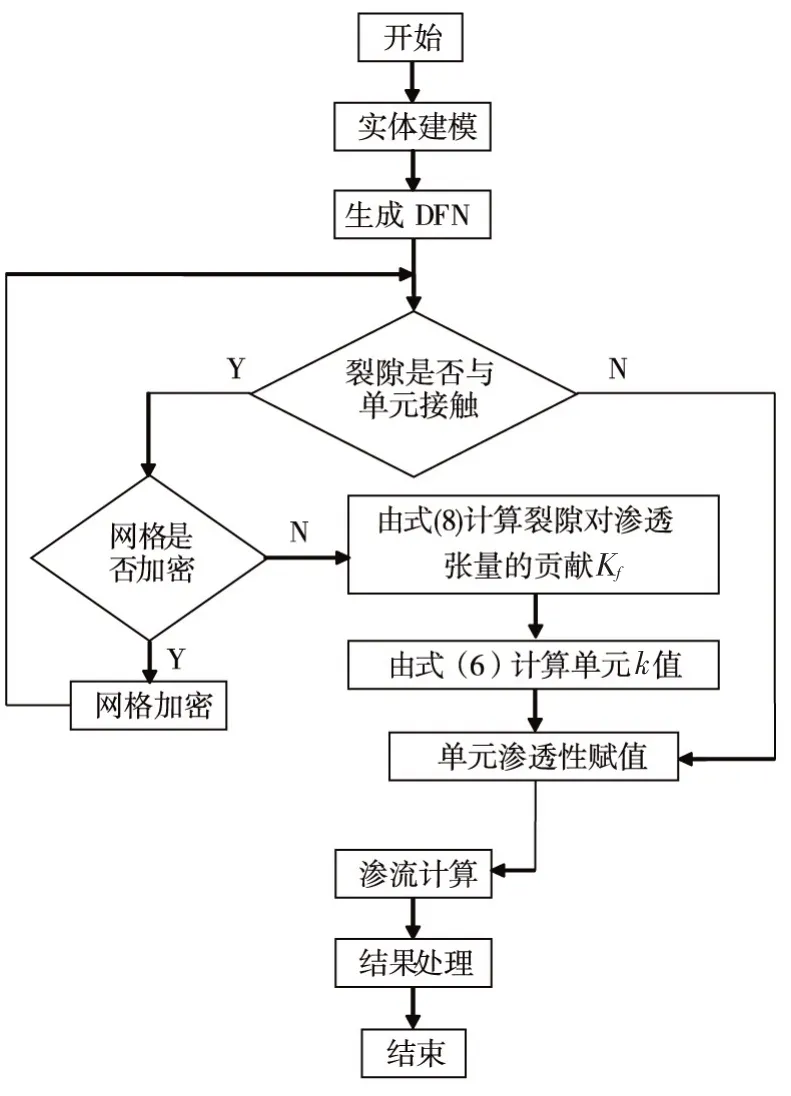
图3 计算流程图

为实现含裂隙的大规模工程岩体渗流分析功能，基于FLAC3D5.01版本提供的DFNs（discrete fracture networks）功能，利用上述技术思路，二次开发了能同时进行渗流分析的连续孔隙单元和裂隙等效单元的FISH程序。需要说明的是，尽管FLAC3D5.01版本提供了DFNs几何信息生成功能，但该软件平台却没有提供如何利用DFNs进行单元离散性质模拟的相关模块或命令，因此，需要进行二次程序开发。程序计算流程如图3所示。（1）建立研究域内的实体单元模型（孔隙单元）；（2）确定离散裂隙的生成域，在同一坐标系下通过蒙特卡罗法生成离散裂隙网络模型；（3）根据给定的裂隙等效单元精度参数和加密参数，对裂隙穿过单元网格进行加密剖分；（4）将与裂隙接触的单元标记为裂隙等效单元，并储存裂隙的几何信息；（5）裂隙等效单元使用各向异性渗流模型，计算域内其余的孔隙介质单元使用各向同性渗流模型；（6）若单元为裂隙等效单元，根据单元中储存的裂隙几何信息按式（8）计算裂隙对渗透张量的贡献，然后利用式（6）计算单元整体渗透张量；若单元为孔隙介质单元，直接使用孔隙介质的渗透系数。单元渗透性计算完成后对单元进行渗透系数赋值；（7）最后施加渗流模型初始条件和边界条件，进行渗流计算。

需要说明的是，在数值模拟过程中，往往需要同时考虑计算精度和计算效率的问题，对于变化平缓的非重点区域需要布置稀疏的网格，而在变化剧烈的重点部位则需要布置密集的网格。因此，在程序分析过程增加了网格加密剖分环节。图4为裂隙单元加密示意图。图中红色圆盘为离散裂隙模型，灰色区域为裂隙单元，白色区域为无裂隙的孔隙介质单元。由图4（a）（d）可知，裂隙等效单元加密前的形状为正方形，与离散裂隙的圆盘形不符；加密后的等效单元形状更加接近于圆盘形。图4（c）（f）则表明，随着裂隙单元的加密，裂隙单元的形状在走向方向上的形状会更精确，所以其渗透张量误差也会越小。由此可见，对裂隙等效单元进行局部加密，可以有效地减小网格剖分带来的误差。

图4 裂隙单元加密示意

4 程序及模型验证

为评价本文提出模型的正确性，分别以具有单一矩形贯穿裂隙岩体和文献[9]中的算例来进行裂隙岩体的渗透性和单一圆形非贯穿裂隙岩体渗透张量的验证。

图5 算例1计算网格

算例1：研究域为一个10 m×10 m×10 m的方形区域，岩块（基质）计算渗透系数取1×10-10 m/s，假设岩体中心有一个贯穿裂隙，隙宽为0.1 mm。如图5，裂隙面与立方体区域中心重合，且裂隙面法向量垂直于x轴与z轴。令水力梯度为1，与水力梯度方向垂直的两面为定水头边界，其余面为不透水边界。

沿x方向上的总流量为裂隙流量和孔隙流量之和，其中裂隙流量Qf根据立方定律[2]求出：

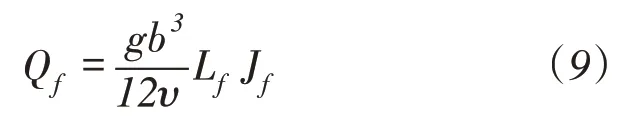
式中：Lf为裂隙的迹长；Jf为沿x方向上的水力梯度。孔隙流量Qr根据达西定律求出。计算得到沿x方向上的裂隙流量Qf为8.250825×10-2 m3/s，孔隙流量Qr为1×10-8 m3/s，所以沿x方向上的总流量Q为8.250826×10-2 m3/s。按照本文研究方法通过数值方法得到模型在x方向上的流量为8.250826×10-2 m3/s，在保留小数点后6位有效数字的情况下，数值计算结果和解析解结果相同。可以看出在岩块透水性较差的情况下裂隙单元中孔隙流量对总流量的贡献基本可以忽略。岩体渗流的优势通道为连通裂隙通道，因此，本文提出的考虑裂隙渗流效应的岩体渗流分析方法较常规连续介质渗流分析方法更加能反映裂隙渗流的优势效应。

图6 算例2几何模型及边界条件示意

算例2：假设边长为20 m立方形岩体中心有一个直径为10 m，隙宽为1 mm的圆盘形裂隙，岩块（基质）计算渗透系数取1×10-8m/s。圆盘圆心始终与立方体区域中心重合，裂隙面法向量始终垂直于z轴，定义α角为y轴与裂隙面法向量形成的夹角，计算α角分别为0°、15°、30°、45°、60°、75°以及90°时的岩体整体渗透张量。令水力梯度为1，与水力梯度方向垂直的两面为定水头边界，其余面上根据与两定水头边界面的位置关系设置为线性变化的变水头边界（见图6）。

根据文献[11]可知该问题中的渗透张量Kf为角度α的函数，且kzz不随α角的变化而变化，Kf可以表示为：

根据文献[1]可知渗透张量各渗透系数随坐标轴旋转而变化，将坐标系xoy顺时针旋转α角，其转换关系为：

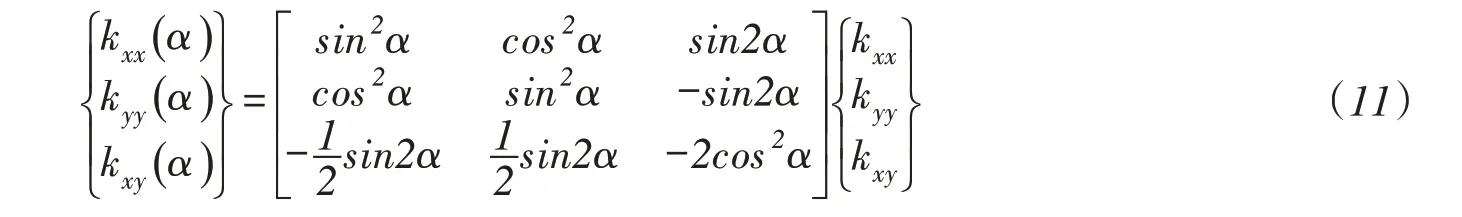
式（10）中的各个元素取值可通过式（11）得到。图7为算例2所述问题的解析解与数值解对比。依据流量等效和边界相同的原则，求得各个面的渗流量后，研究域的渗透张量可参考文献[24]方法确定。由图可知，渗透张量的理论解和数值解在整体上吻合度很好，说明本文采用的含裂隙介质的渗流分析方法是合理可行的。

5 单元尺度大小对研究域等效渗透性影响分析

假设边长为20 m立方形岩体中心有一个直径为10 m，隙宽为1 mm的圆盘形裂隙。圆盘圆心与立方体区域中心重合，裂隙面法向量与Y轴平行。单元未加密时裂隙单元边长为2 m，加密后使裂隙单元边长分别为1、0.5和0.25 m。岩块（基质）计算渗透系数取1×10-8 m/s。通过比较不同加密程度后研究区域的整体渗透性，来研究加裂隙附近单元的加密程度对渗透性的影响。

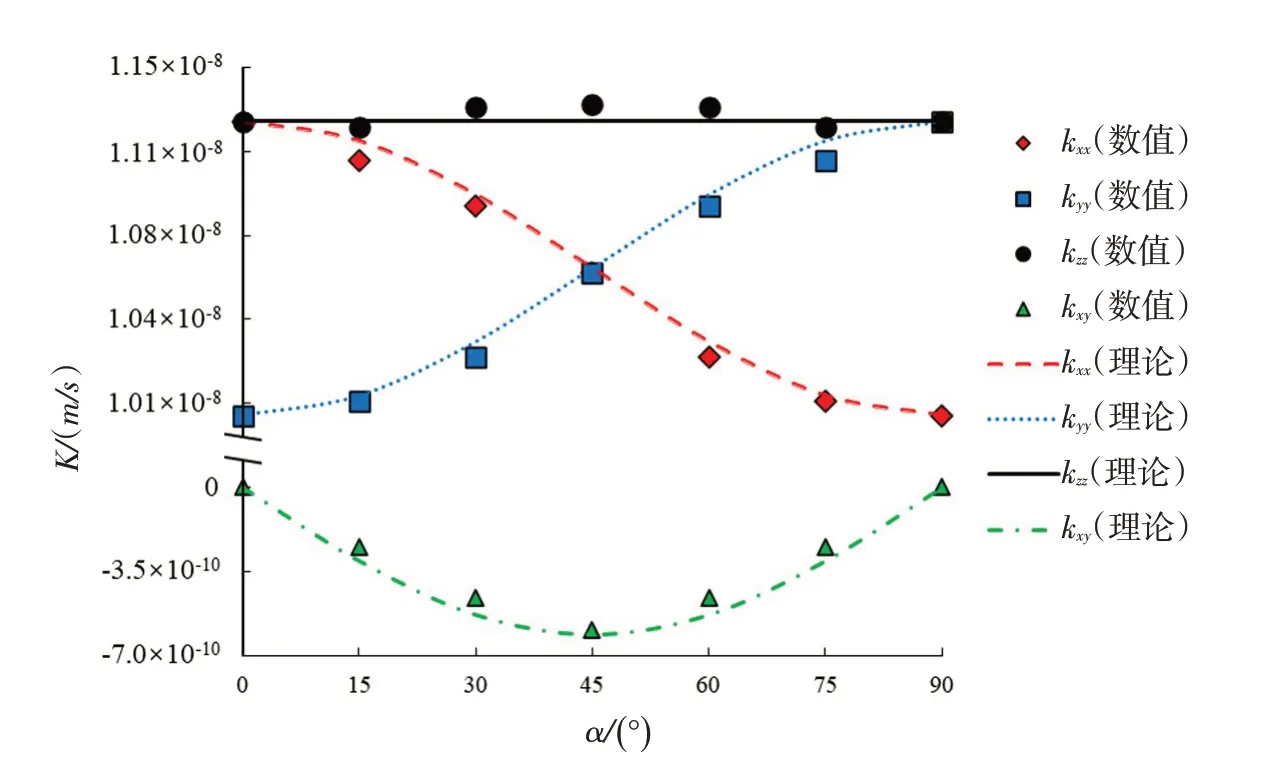
图7 渗透张量数值解与理论解对比

图8 剖面y=10m处单元尺度对比

在图8中白色区域为基质单元，深灰色区域为裂隙单元，白色圆圈为圆盘离散裂隙。随着裂隙单元边长不断缩小，裂隙位置处的灰色区域形状逐渐从方形接近圆形，即裂隙影响的基质单元范围越来越小。表1给出了包含裂隙的单元尺寸变化对应的研究域计算渗透系数变化情况，其中研究域的计算渗透系数是根据各个面的渗流量，通过达西定律计算得到的整个研究域的渗透系数。图9为依据表1绘制的计算与渗透性与单元尺度变化关系。由表1和图9可知，由于裂隙没有穿透基质岩石，故研究域综合渗透性主要受基质渗透性控制；但裂隙的存在使得水流在x和z方向的渗透性出现了一定程度的增加，但其计算渗透性的增加幅度与穿越裂隙单元的尺寸大小相关。随着裂隙处单元边长不断减小，计算渗透系数基本呈线性减少的趋势。含裂隙单元尺寸越小，得到的研究域内计算渗透系数约接近于真实值。单元尺度由0.25 m增加到2.0 m后，两者间的计算误差可达到19.1%。理论上，在裂隙未贯穿的情况下，研究域内整体的渗透性均由基质岩块的渗透性控制。需要说明的是，对于实际岩块被裂隙贯穿的单元，其渗透张量计算值不受计算单元尺度大小的影响。因此，在计算中为尽量减少误差，可只需对裂隙边界单元采用较小的单元尺度即可。

图9 渗透系数与单元尺度关系

表1 计算渗透系数与单元尺度关系表

6 坝基裂隙岩体渗流效应分析

对于重力坝坝基而言，坝基岩体中分布的裂隙对于坝基扬压力与渗流路径的空间分布规律有着重要的影响。为了解坝基岩体中的裂隙分布对渗流场的影响，拟定如图10所示的三种计算模型进行分析。模型一中的裂隙总体倾向下游；模型二坝基岩体中的裂隙总体倾向上游；模型三坝基岩体中不考虑裂隙影响。坝基岩体中裂隙统计数据如表2，隙宽均为1 mm。模型一和模型二中裂隙穿过的计算单元为各向异性渗流单元，其余为各向同性渗流单元；模型三中的计算单元均为各向同性渗流单元。含裂隙单元的渗透系数按式（6）和式（8）由程序自动计算，坝基岩块渗透系数取1×10-7m/s。考虑到坝体混凝土渗透性相对较小，本算例分析时视为不透水介质。三个计算模型的上游水头均为40 m，下游水头均为10 m，计算坝基的稳定性渗流场。

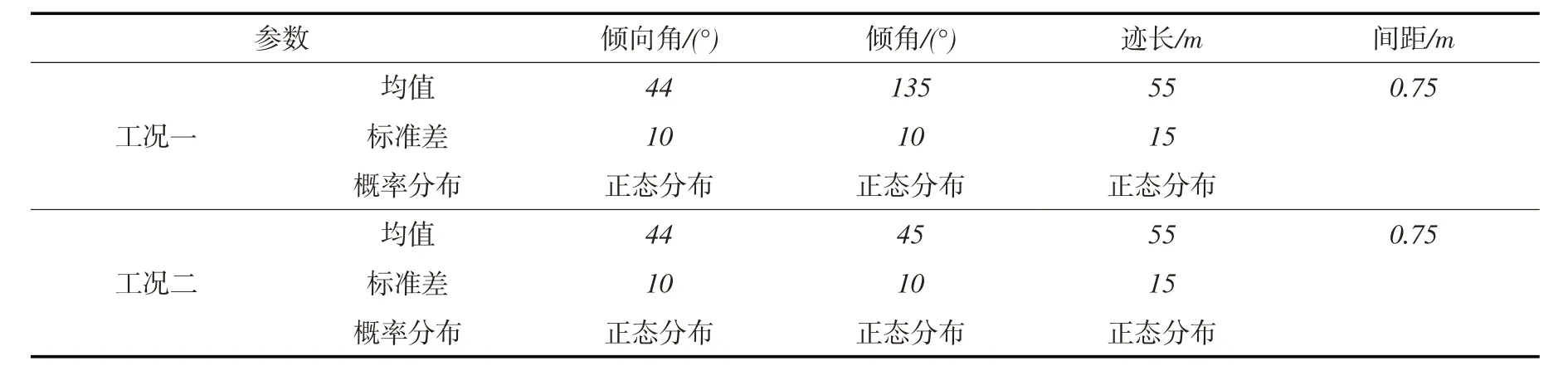
表2 裂隙统计参数表

图10 模型计算网格图

图11给出了边界条件相同情况下坝基岩体中的部分流线分布图。由图可知，坝基中存在导水裂隙时，水流路径主要沿裂隙通道分布。由此可见，考虑裂隙分布影响的ELE模型能够反映坝基岩体渗流的真实路径。裂隙产状对坝基孔隙压力的空间分布形态也存在显著影响，如图12所示。裂隙分布状态对坝基扬压力分布规律也将产生不同程度的影响，如图13所示，裂隙分布的随机性是导致坝基扬压力分布的非规则性的直接因素。考虑裂隙分布随机性导致的坝基扬压力分布的非规则性与坝基扬压力的实测分布更为接近。总之，EFE模型可以很好地模拟离散裂隙的局部导水和疏水性能，从而真实有效地反应坝基裂隙岩体的渗流状态。

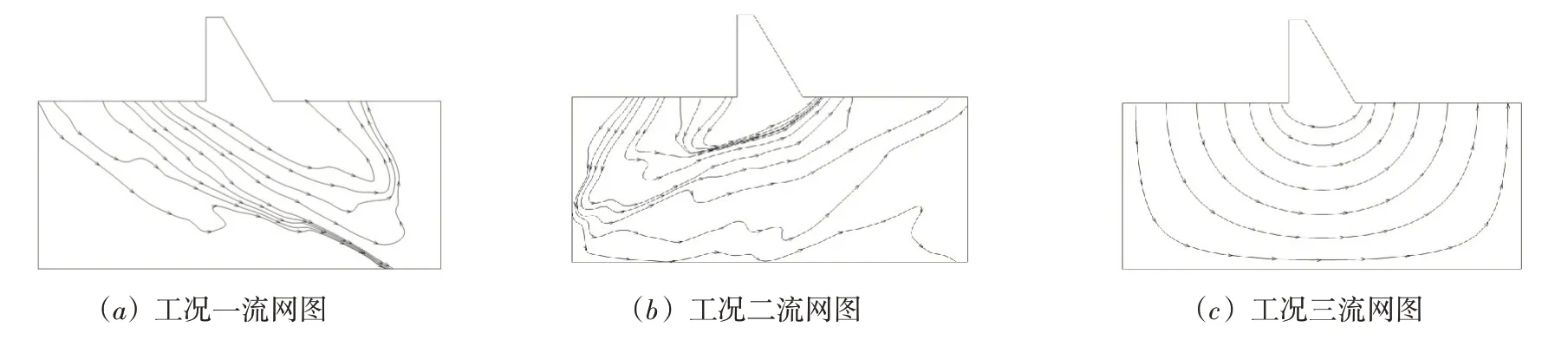
图11 坝基岩体中流网图

图12 坝基岩体中水压力图（单位：1×104Pa）

图13 坝基扬压力分布

7 结论

本文提出嵌入裂隙单元模型，并在FLAC3D软件平台上完成了程序实现。基于裂隙岩体渗流理论研究的基础上，提出并实现了利用连续介质各向异性渗流模型模拟裂隙渗流特性的数值分析方法，并验证了方法的合理性。（1）将离散裂隙网络（DFNs）技术与连续介质各向异性渗流分析技术结合，利用构造的EFE渗流单元模拟裂隙导致的各向异性非均匀渗流效应效果，能够真实反映裂隙随机分布所导致的各向异性渗透特性。（2）理论上使用EFE单元数值模型分析真实裂隙渗流问题必然会存在一定的误差，可以通过调整裂隙边界处的EFE单元尺度大小来降低这种误差。（3）本文提出的裂隙岩体渗流的连续介质数值模拟方法可适用于工程尺度的大规模数值计算，其计算效率和精度均能满足工程要求。