复杂防洪系统优化调度的三层并行逐步优化算法
朱 迪,梅亚东,许新发,刘章君
(1. 武汉大学 水资源与水电工程科学国家重点实验室,湖北 武汉 430072;2. 江西省水利科学研究院,江西 南昌 330029)
1 研究背景
洪水灾害是我国发生频次高、危害范围广的自然灾害。据统计,1951年至1990年期间,我国平均每年发生5.9次严重洪水灾害;1991年至2008年期间,我国洪水灾害造成21 163亿元直接经济损失,约占整个自然灾害经济损失的48%[1]。防洪系统中水库群的建设和运行调度,是防洪减灾的重要措施[2]。然而防洪系统的复杂水文、水力联系,使得防洪优化调度问题具有强约束、多阶段、非线性和高维度等特点[3],其求解值得进一步探讨。目前,常用的防洪优化调度求解方法有传统优化算法和智能优化算法[4]。传统优化算法以线性规划算法[5]、分解协调算法[6]、动态规划及其改进算法[7-9]等为代表,而智能算法发展了一批诸如遗传算法[10]、粒子群算法[11]、差分进化算法[12]等模拟自然过程的优化算法。线性规划算法、分解协调算法等需要对调度模型进行近似处理,优化求解结果存在一定误差[13];智能优化算法因为随机性因素的存在,求解结果并不稳定。动态规划算法对于此类多阶段序贯决策问题,求解结果稳定且优化效果好,而被广泛用于水库优化调度领域。但是防洪系统中,洪水演进造成的滞后性,不满足动态规划算法无后效性的要求,且水库数目的增加,又带来“维数灾”问题。
逐步优化算法(Progressive Optimality Algorithm,POA)由Howson和Sancho于1975年提出,是用于解决多阶段的动态决策问题的优化算法[14]。POA算法将多阶段决策问题分解为一系列两阶段子问题进行求解,可以处理有后效性的问题,并在一定程度上缓解“维数灾”。但是复杂防洪系统除了考虑水库群的防洪调度,还需要考虑其它水利工程(航电枢纽、分蓄洪区)防洪调度、区间入流和洪水演进对防洪效果的影响等因素,具有求解变量数目较多,水文、水力联系复杂,约束条件多等特点,采用POA算法求解存在计算效率低,优化结果易局部收敛等问题。因此,本文提出了三层并行逐步优化算法(Triple Parallel Progressive Optimality Algorithm,TPPOA)。该算法基于POA算法与启发式算法算子相结合的思路[15],通过引入莱维飞行扩大寻优范围,更新调度策略,改善解的质量[16];在算法迭代后期,引入模式搜索,在进一步优化的同时,增加求解的稳定性[17];引入并行技术[18],以提高求解速度,并以赣江中下游复杂防洪系统优化调度为实例进行验证分析。
2 复杂防洪系统调度模型
考虑以串联水库—航电枢纽—分蓄洪区—防洪控制点构成的复杂防洪系统,假设系统中有I座串联梯级工程(水库、航电枢纽等),N个防洪对象(防洪控制点)和S个分蓄洪区,其中第i个工程第j个防洪控制点和第s个分蓄洪区联系概化图如图1所示,第t时段初水力联系如式(1)所示:
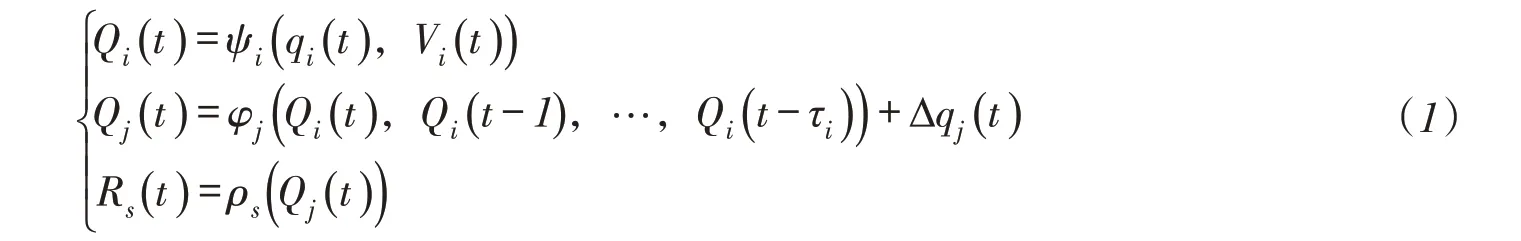
式中:Qi(t),qi(t),Vi(t)分别为第i工程第t时段初泄水流量,来水流量和蓄水量;τi为第i工程泄水流量演进至第j控制点的时滞;Qj(t)为第j防控制点第t时段流量;Δqj(t)为第j个防洪控制点区间入流;Rs(t)为第s个分蓄洪区第t时段初分洪流量;ψi(·)为第i工程防洪调度决策函数;φj(·)为第i工程至第j控制点之间水流演进函数;ρs(·)为第s分蓄洪区运用规则函数。
由此可知,复杂防洪系统的复杂性体现在:相较一般的单一水库防洪系统,需要考虑水库群联合防洪调度、水库出库洪水在河道的演进以及区间入流的汇合;相较传统梯级水库防洪系统,则需要考虑其他水利工程在防洪期间的运行。
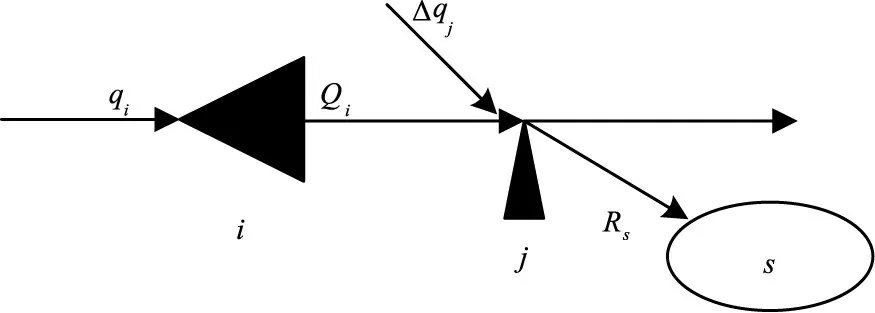
图1 水库-分蓄洪区-防洪控制点联系示意
2.1 目标函数防洪系统调度的主要目的是在保障相关水利工程安全运行条件下,尽可能利用水库防洪库容、分蓄洪区容积,蓄滞洪水,调峰错峰,削减下游防洪控制点洪峰。对于存在多个防洪控制点的流域复杂防洪系统,可根据各防洪控制点的重要性差异进行赋权,目标函数可按下式表达:

式中:Qs,j为天然情况(无防洪调度情形)下第j个防洪控制点的洪峰流量;Qf,j为在防洪优化调度情况下第j个防洪控制点的洪峰流量;αj为第j个防洪控制点的权重系数;N为防洪控制点个数。
2.2 约束条件
(1)水库水量平衡约束:

式中:qi(t)、qi(t+1)为第i个水库第t时段初、末入库流量;Qi(t)、Qi(t+1)为第i个水库第t时段初、末出库流量;Vi(t)和Vi(t+1)为第i个水库第t时段初、末的库容;Δt为调度时段长。
(2)水库最高、最低水位约束:

式中:Zi(t+1)为第i个水库第t时段末水位;Zimin、Zimax分别为第i个水库调度期内所允许达到的最高和最低水位。
(3)水库调度期初、末水位约束:

式中:Zi(1)、Zi(T+1)为第i个水库调度期内初、末水位;Zi,start、Zi,end分别为第i个水库起调水位和期末水位。
(4)水库泄流能力约束:

式中:Qimax[Zi(t+1)]为第i水库t时段末水位为Zi(t+1)时的最大泄流能力。(5)水库泄流变幅约束:

式中:ΔQi为第i水库第t时段允许的最大泄流变幅。
(6)洪水演进约束:
从水库(或航电工程)下泄洪水经河道演进到下游控制点(或工程)断面,其间接受区间洪水汇入。将每个河段划分为若干个子河段数,对于第m子演进河段,假设河段下断面有区间洪水汇入,第m子演进河段洪水演进方程如下:
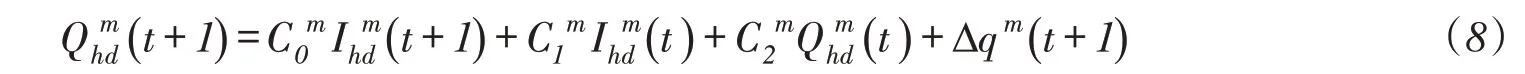
(7)其他工程约束:
复杂防洪系统中航电枢纽、分蓄洪区等其他工程,对洪水演进起到一定的阻滞、分蓄作用。对于此类工程约束,可按其常规防洪调度规则进行模拟。
航电枢纽一般不设防洪库容,在防洪期间具有阻滞洪水的作用,其作用通过下式表达:

式中:Qout,k(t)、Qin,k(t)、Zs,k(t)分别为第k工程第t时段初下泄流量、来水流量及坝址水位;fk(·)为第k工程洪水调度规则。
分蓄洪区的作用是削减威胁下游重点保护河段的洪峰流量,其分蓄流量根据断面上游洪峰流量及其抵达分蓄洪区控制断面的时机、分蓄洪区容积等因素决定。当洪水具有持续上涨趋势时,分洪断面水量关系如下式:
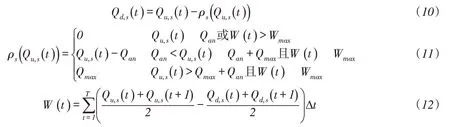
式中:Qd,s(t)、Qu,s(t)、ρs(Qu,s(t))、Qmax、Qan分别为第s分蓄洪区第t时段断面下泄流量、断面上游来水流量、分洪流量、分蓄洪区最大分洪流量以及下游河段安全泄量;W(t)和Wmax分别为分蓄洪区第t时段已蓄水容积和允许的最大分蓄容积。
(8)非负约束:
所有变量均为非负变量。
3 求解方法
3.1 逐步优化算法POA将复杂多阶段决策问题转化为多个两阶段子问题,求解时,固定其他时段决策,仅优化当前时段决策,然后逐个时段优化求解直至收敛。具体步骤如下:(1)确定各水库初始可行调度解u={V1(1),V1(2),…,V1(T+1),…,Vi(t),…,VM(1),…,VM(T+1)},i=1,2,…,M,为水库数目;(2)在水库库容上下限范围内离散第i水库t时刻(t=2~T)库容为(3)固定Vi(t-1),Vi(t+1),按步骤(2)中离散点调整Vi(t),遍历第i水库所有时段;(4)重复步骤(2)、(3),遍历所有水库,得出优化调度解(5)以u*作为初始调度解,重复步骤(3)(4)进行迭代计算,以前后两次迭代计算的目标函数值的差值是否达到误差限作为迭代终止条件;(6)如果达到迭代终止条件,以u*作为最终优化调度解。
传统POA算法是给定离散精度,对各水库各时段决策采用网格搜索。当水库数目或调度决策较少,水力联系较简单时,求解速度快,效率较高。然而随着防洪系统复杂性的增加,传统POA算法存在计算时间长,求解效率低等问题。此外在POA算法迭代后期,优化结果也容易陷入局部最优[19]。为提高POA优化效率,本文提出了三层并行逐步优化算法(TPPOA)。
3.2 三层并行逐步优化算法POA在优化水库调度决策过程中,水库出库流量是已知的,因此可以采用模拟技术处理洪水演进、其它水利工程的调度、支流汇入等约束和水力联系。然而并不是所有时段的调度决策会影响防洪控制点的洪峰流量,例如:在涨洪期和退水期的调度决策优化,可能不影响下游洪峰的削减,但是却需要占用计算资源并增加计算时间。TPPOA算法相较传统POA算法,增加了识别主要调度决策的步骤,通过更新主要调度决策进行优化,以节约计算资源;在更新主要调度决策中,引入莱维飞行策略,以扩大搜索范围,减小陷入局部最优的机率;参考matlab中遗传算法、粒子群算法等优化工具箱以模式搜索法对优化结果作进一步处理的思路,在优化过程后期,本文采用模式搜索法对所有调度策略进行优化更新;此外,将并行技术引入算法,进一步加快算法计算速度。
3.2.1第一层POA算法 第一层POA算法与一般POA算法不同之处是,引进了确定主要调度决策的差分指标。差分指标定义如下:

式中:Un为在第一层POA算法中第n次迭代后的差分指标值;Vi,n(t)为第i个水库第t时段的第n次迭代库容值;R(*)为阶跃函数[20],计算公示如下:
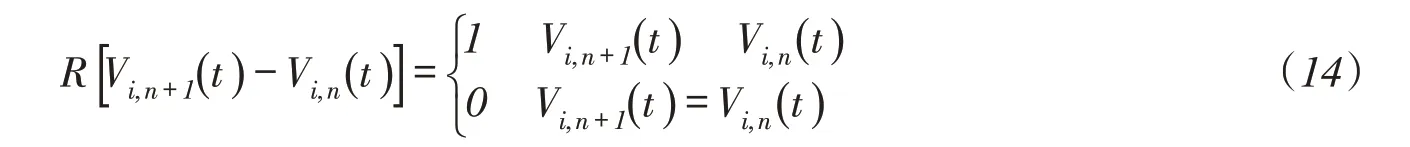
差分指标Un反映的是第n+1次迭代和第n次迭代前后,改变的调度决策数目。当|Un+1-Un| 1时,可以认为在第n次迭代后,调度决策数目收敛,此时只有一部分调度决策在后续优化过程中迭代更新。这部分调度决策构成主要调度决策集合,进入第二层POA算法,对其进行优化更新。设un={V1,n(1),V1,n(2),…,V1,n(T+1),…,Vi,n(t),…,VM,n(1),…,VM,n(T+1)}表示第n次调度决策集,按式(15)对比un和un+1,找到主要影响决策如式(16)所示。
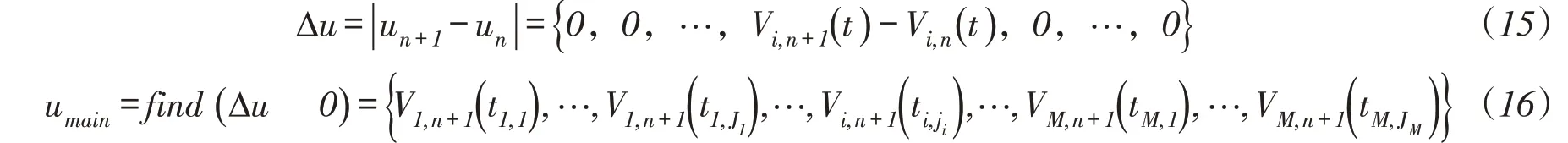
式中:Δu为和的向量差;find(Δu)为找到Δu中不为0的元素对应的库容,构成主要影响调度决策集;ti,ji为主要调度决策序号,Vi,n+1(ti,ji)为第i个水库,第ti,ji个主要调度决策值,对于第i个水库,共有Ji个。
3.2.2第二层POA算法 在第二层优化计算中,基于主要调度决策集umain,采用莱维飞行进行进一步搜索更新。莱维分布是法国数学家莱维(Lévy)提出的一种概率分布[16],而莱维飞行是一种服从莱维分布,模拟自然界中动物觅食的随机搜索路径[21]。因其具有扩大搜索范围的特性,莱维飞行被不少学者用于优化领域[22-24]。本文将莱维飞行与POA算法相结合,对主要调度决策进行更新,其更新计算公式如下:
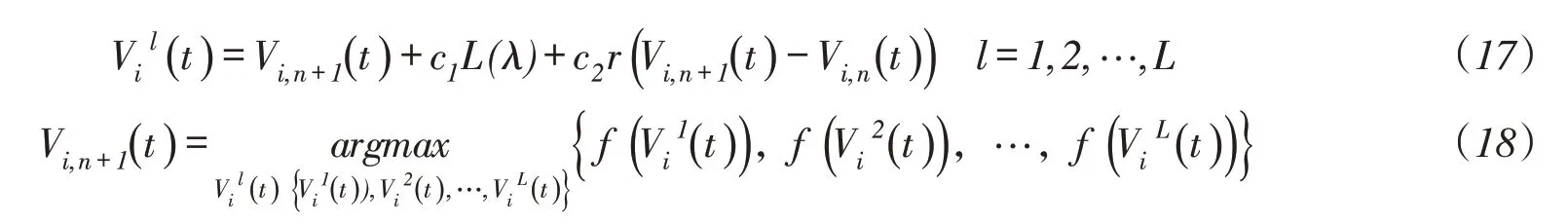
式中:Vi,(nt)为在第二层POA算法中第i个水库第t时段n次迭代后的库容决策值;r为[0,1]内均匀分布的随机数;c1和c2为步长控制量;为第i个水库第t时段第l个子迭代决策值;(f*)为适应度函数,表示防洪控制点洪峰削减率;L(λ)为莱维分布随机搜索路径,由于莱维分布十分复杂,目前采用Mantegna算法[16]进行模拟:

式中:μ和ν为正态分布,定义如下:

其中,
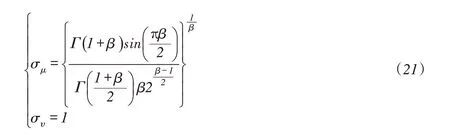
通常β取值为1.5。
耦合莱维飞行的POA算法求解步骤为:(1)以第一层POA算法得出的初始解V1(t1,2),…,Vi(ti,ji),…,VM(tM,JM)}作为初始解。为叙述方便,重新整理各水库主要调度决策序号,整理后的主要调度决策umain={V1(1),V1(2),…,Vi(ti),…,VM(TM)};设置迭代次数k=1。(2)对于ti=2~Ti,固定Vi(ti-1),Vi(ti+1),按式(17)、(18)更新Vi(ti),得出优化解Vi*(ti)并遍历第i水库所有调度决策。(3)重复步骤(2),遍历所有水库,完成主要调度决策更新(4)判断是否达到终止条件,若相邻两次迭代后的目标函数值相差值在误差范围内,则输出优化调度解u*main;否则以u*main作为初始解,转步骤(2)。
3.2.3模式搜索法 模式搜索法以坐标轮换法为基础[17,25],包括沿坐标轴方向寻优的探测移动和沿两个相邻点连线方向寻优的模式移动。其模式搜索具体步骤如下:(1)将第二层算法得出的调度解u*定为初始点,初始步长αp>0,精度εp,坐标方向ej=(0,…,1,…,0)T,j=1,…,M*(T-1),M*(T-1)为u*中调度决策的数目,设置Y1=u*,迭代次数k=1。(2)对于j=1,2,…,M*(T-1),若f(Yj+αpej)<f(Yj),则Yj+1=Yj+αpej;否则,若f(Yj-αpej)<f(Yj),则Yj+1=Yj-αpej;否则Yj+1=Yj。(3)若f(Yn+1)<f(uk*),则有转步骤(2);否则转步骤(4)。(4)若αp<εp,则停止计算,得出优化解uk*;否则α=α/2,转步骤(1)。
3.2.4多核并行计算 随着计算机的计算能力的不断增强,并行计算发展为一种提高算法计算速度的有效手段,其基本思想是将被求解的问题分解为若干部份,各部分由独立处理单位同时进行计算,以空间复杂度来换取时间复杂度[26],提高算法计算效率。本文选择matlab parfor并行计算方式,matlab parfor要求各计算任务具有独立性,不存在数据依赖。通过对算法计算特性进行分析可知,在第一、二层POA算法中,各调度解的循环迭代计算任务具有独立性,可将串行迭代循环的不同阶段划分为独立的子任务[18],分配到计算机的不同CPU计算核心中。设计并行计算思路如图2所示,假设初始可行解确定,计算核心CPU有P个,阶段内的离散点个数有N个;普通POA算法采用串行迭代循环,需要对阶段内循环迭代N次,从中得出该阶段的最优解;而并行迭代计算,是将阶段内的计算任务分配至P个计算核心上,每个计算核心只需要N/P次就可以得出优解,计算速率得以加快。在模式搜索算法层中,本文采用matlab patternsearch工具箱进行并行加速。
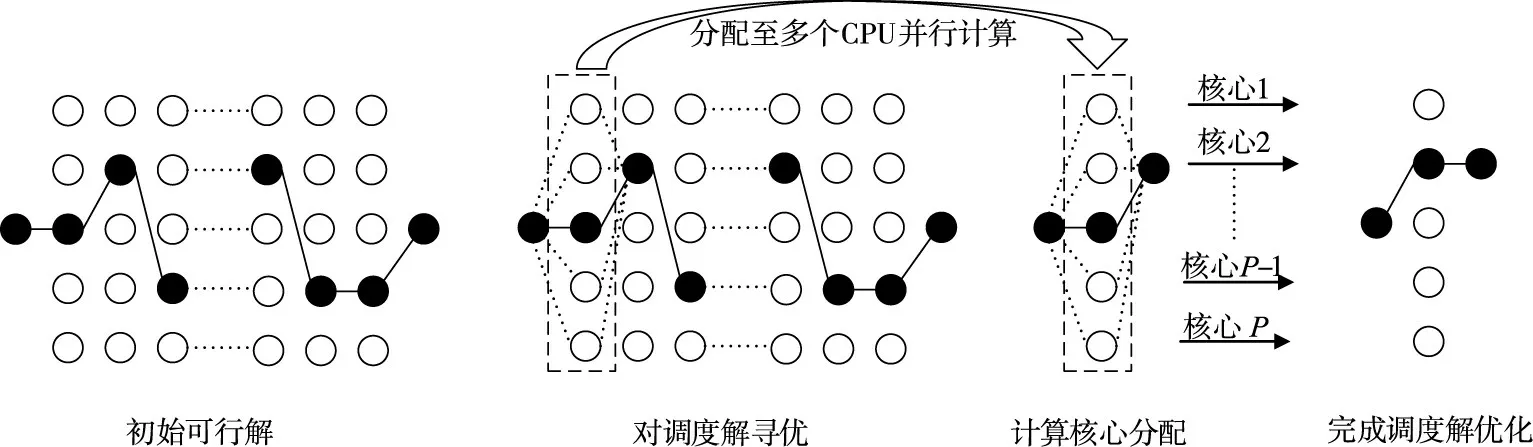
图2 并行计算示意
3.2.5多核并行计算 三层并行POA算法计算流程如图3所示:
(1)输入计算数据,包括:洪水流量资料、水库资料、计算参数设置。
(2)采用POA算法进行计算并结合多核并行技术,并采用式(11)计算调度解集的差分指标,判断是否结束迭代计算。当相邻迭代计算前后差分指标的差值小于1时,跳出POA计算层,输出主要调度决策集umain,转步骤(3);否则,继续进行步骤(2)。
(3)基于umain,采用式(17)—(21)结合多核并行技术进行调度解的更新,当相邻两次迭代计算的目标函数误差值小于误差限时,输出优化调度解集u*,转步骤(4),否则,继续进行步骤(3)。
(4)基于优化调度解集u*,采用并行模式搜索法进行优化,得出最终优化调度解集。
4 实例研究
4.1 流域防洪系统概况赣江中下游万安—峡江梯级所组成的防洪系统概化图如图4所示。该防洪系统包括万安和峡江水库,井冈山、石虎塘、新干、龙头山等4座航电枢纽,泉港分蓄洪区,吉安、石上和外洲等3个防洪控制点以及多条区间入流,各水库主要特性参数如表1所示。根据赣江流域综合规划[27],井冈山等4个航电枢纽不承担防洪任务,故万安-峡江梯级为本文防洪优化调度的主要对象,而泉港分蓄洪区根据下游赣东大堤和南昌市城市防洪堤的安全泄量决定其启用条件。当泉港分洪闸上游石上断面流量超过24 000 m3/s或闸外赣江水位达到31.12 m且洪水继续上涨时,打开泉港分洪闸实施分洪,分洪时控制闸门开启高度,使闸外赣江水位维持在31.12 m不变。
4.2 数据资料与计算条件本文采用1961年、1973年和1994年按外洲站洪峰放大的200年一遇设计洪水资料,计算时长为6 h。干流洪水流量、区间入流以及马斯京根参数等资料由江西省水利科学研究院提供。万安和峡江水库调度期初和期末水位为各自汛限水位,万安水库调度期内最高水位为93.6 m(防洪高水位),峡江水库优化调度最高水位为常规防洪调度期内最高水位。以万安和峡江水库常规防洪调度结果作为初始解,三个防洪控制点权重系数均为1/3,POA算法中水库库容离散点数目为30,前后两次迭代目标函数差值为0.0001;第二层POA算法中子迭代次数L=30,模式搜索层中,初始步长α=50,εp=0.0001。采用计算软件为matlab 2018b,运行环境为win10操作系统,Intel(R)Core(TM)i7-8700 CPU,3.2 GHz,RAM 16.00 G,采用6核并行计算。
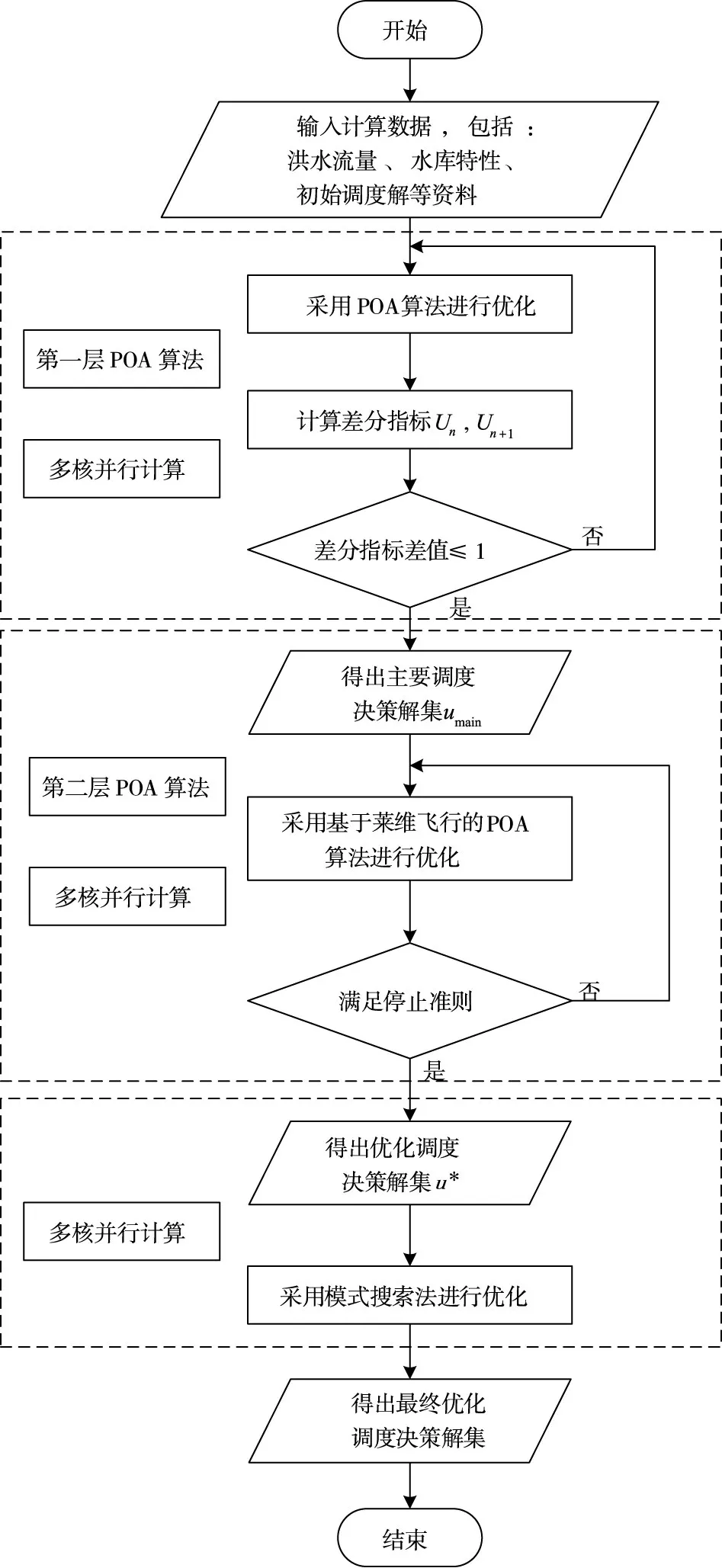
图3 TPPOA算法流程

图4 赣江中下游防洪调度系统概化图
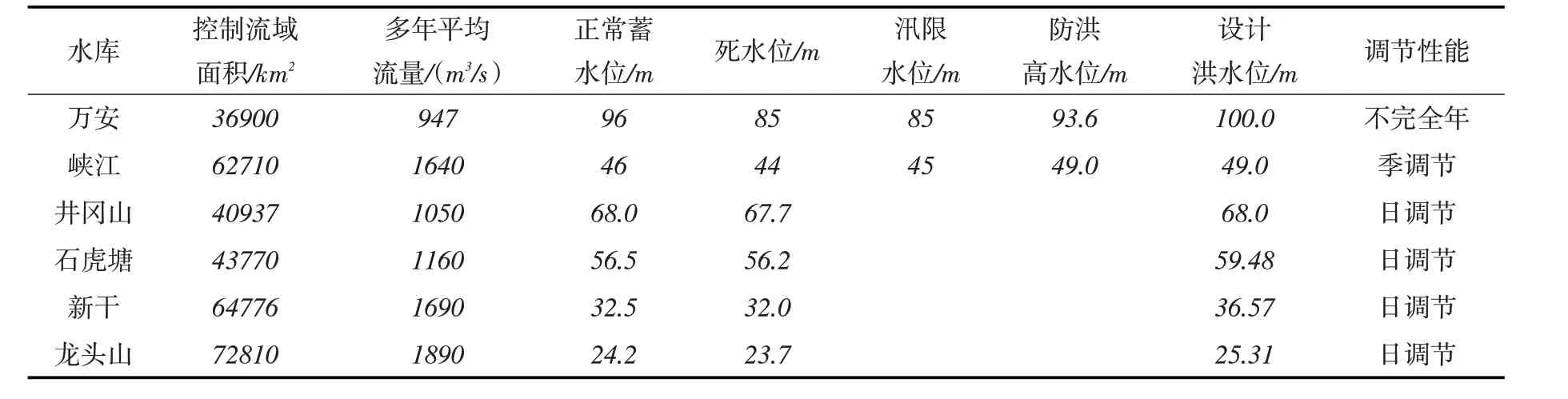
表1 各水库主要特性参数
4.3 计算结果分析采用TPPOA对三种典型设计洪水的赣江中下游防洪系统调度进行了优化,计算结果列于表2。同时表2还给出了采用常规防洪调度规则和采用普通POA算法获得的结果。图5至图7给出了三种方法的3个防洪控制点的洪峰流量,其中天然情况对应的是所有工程未建,洪水在天然河道内演进情形。图8至图10给出了万安—峡江梯级水库分别采用常规防洪调度、POA和TPPOA防洪优化调度过程结果,图11为下游吉安和外洲防洪调度后的流量过程。
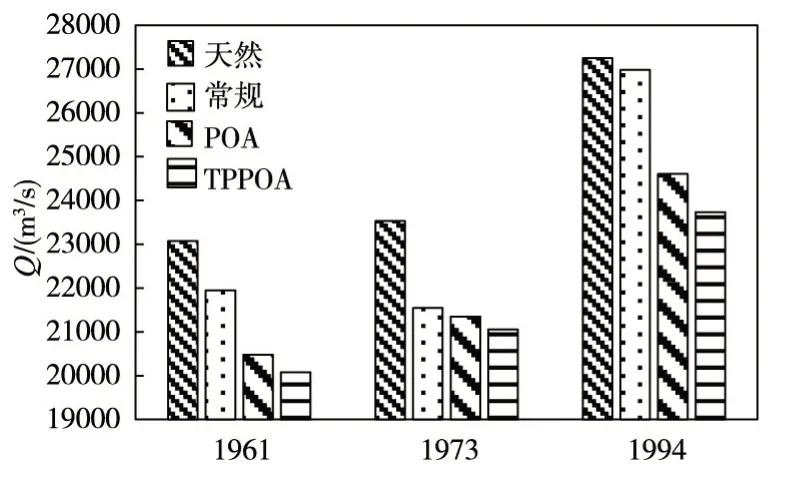
图5 吉安站洪峰流量

图6 石上站洪峰流量

图7 外洲站洪峰流量
从图5至图7可知:对于各典型年200年一遇设计洪水,常规防洪调度、POA和TPPOA的防洪优化调度均能在一定程度削减防洪控制点的洪峰流量。其中,相较其他调度方式,各设计洪水经TP⁃POA优化调度后的防洪控制点洪峰流量最低。从表2可知:对于“1961”设计洪水,常规防洪调度下的泉港分蓄洪量为0,吉安、石上和外洲洪峰削减流量分别为1128 m3/s、4428 m3/s和3953 m3/s;而TP⁃POA优化防洪调度后,三站洪峰削减流量分别为2995 m3/s、5833 m3/s和4790 m3/s,洪峰削减效果较为明显。对于“1973”设计洪水,常规防洪调度后的泉港分蓄洪量为0.04亿m3,而采用TPPOA算法优化调度下的泉港分蓄洪量为0,三站洪峰削减流分别相较常规防洪调度和POA优化防洪调度增加了489 m3/s、1272 m3/s和667 m3/s以及291 m3/s、334 m3/s和232 m3/s。对于“1994”设计洪水,TPPOA算法相较POA算法,吉安和外洲洪峰流量削减增加了869 m3/s和125 m3/s。
从图8(a)、图9(a)和图10(a)可知:万安水库入库洪水为多峰型,其中,1961典型有3个洪峰,主峰为第3个洪峰,峰现时间为第51时段,较为靠后;1973典型有2个洪峰,主峰为2个洪峰,峰现时间居中,为第35时段;1994典型有2个洪峰,2个洪峰流量大小相近,且峰现时间分别为第31和42时段,相隔较为接近。常规防洪调度后,万安水库在主峰出现前没有回落至较低水位,意味着部分防洪库容被占用,使得主峰削峰效果稍差。而采用POA和TPPOA算法进行防洪优化调度后,万安水库水位在入库洪水主峰出现前,基本回落至汛限水位,以腾出库容,削减主峰。从图8(b)、图9(b)和图10(b)可知:万安水库出库洪水经洪水演进、支流汇入、航电枢纽防洪调度后,峡江入库洪水较为宽胖。对于各典型设计洪水,采用TPPOA算法优化防洪调度后的峡江入库洪峰最小,常规防洪调度后的峡江入库洪峰最大,这说明万安水库的防洪优化调度,有利于下游峡江入库洪峰的削减。从图11(a)(c)(e)也可看出,采用TPPOA算法优化防洪调度后的吉安洪峰相较常规防洪调度更低。此外,对于1973典型和1994典型,常规防洪调度后峡江水库的出库洪峰比优化防洪调度后出库洪峰要小,但是从下游防洪控制点洪峰流量上看,如图11(d)(f)所示,优化防洪调度后的外洲洪峰相较常规防洪调度更低,说明优化防洪调度的峡江下泄流量通过与下游汇入的支流洪峰形成错峰补偿,以削减外洲洪峰。
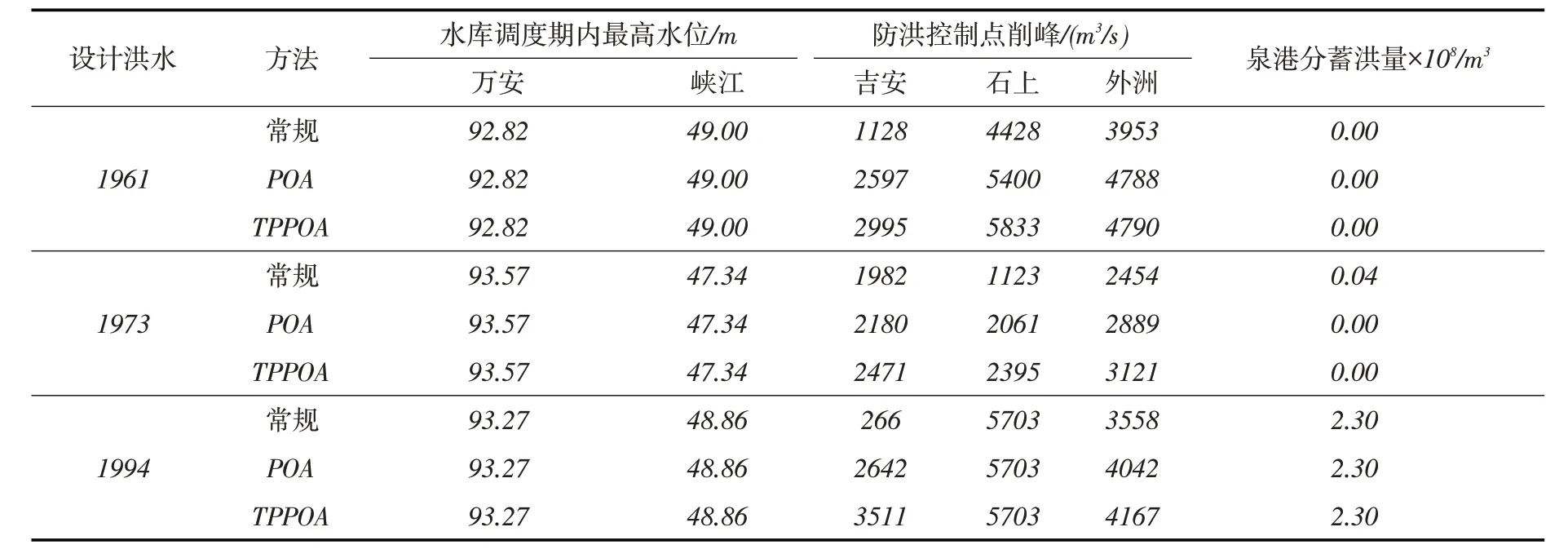
表2 不同方法的防洪调度结果对比
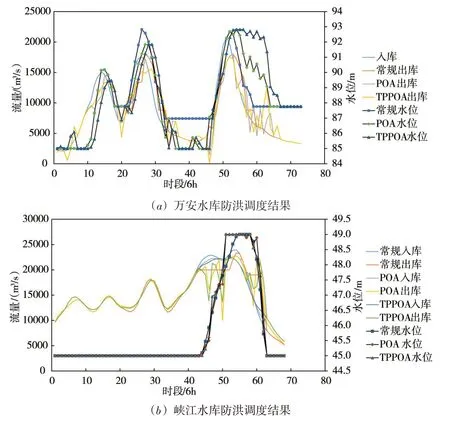
图8 1961年梯级水库防洪调度过程

图9 1973年梯级水库防洪调度过程
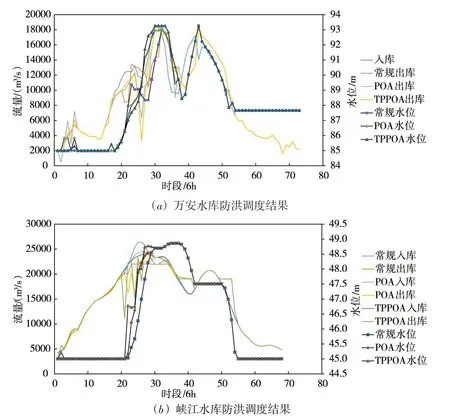
图10 1994年梯级水库防洪调度过程
为对比分析算法计算时间,采用并行POA算法在相同计算条件下,对上述洪水进行优化防洪调度,POA算法、并行POA算法和TPPOA算法计算时长对比如表3所示。从表3可知:POA算法计算时长大于并行POA算法和TPPOA算法。POA算法的计算时长大于TPPOA算法。本文采用6核并行计算,由于计算核心间的通信损失,POA算法计算时长约为并行POA算法的6倍。对于“1961”设计洪水,POA算法计算时长为TPPOA算法的6.95倍,TPPOA算法计算速度相较POA算法更快,这是因为TPPOA算法的第二层算法对主要调度决策进行优化更新,节省计算资源,加快了计算速度。对于“1973”和“1994”设计洪水,POA算法计算时长分别为TPPOA算法的2.91倍和4.37倍,并行POA算法计算时长比TPPOA短。这主要是由于并行POA算法在迭代5次后就陷入局部最优解,计算时长较短。从整体上看,TPPOA算法计算速度高于POA算法,并且防洪控制点的削峰流量相较常规防洪调度规则和POA算法均有提升。
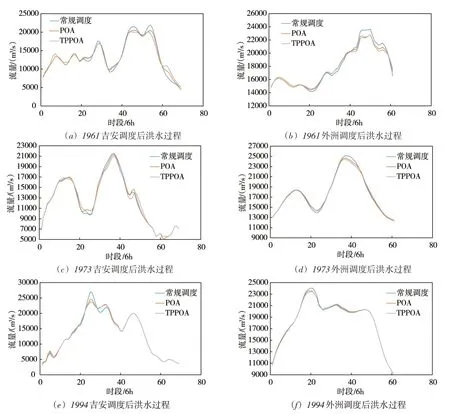
图11 防洪控制点调度后流量过程

表3 不同优化算法计算时间比
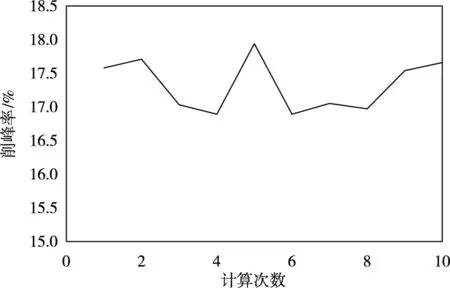
图12 TPPOA算法多次优化结果
为分析莱维飞行的随机性对最优解的影响,采用“1961”设计洪水进行10次计算,削峰率结果如图12所示。削峰率是按式(2)进行计算,其它计算条件设置同4.2节。从图12可知:经过10次优化计算,吉安、石上和外洲防洪控制点的加权平均削峰率在17%~18%左右,莱维飞行的随机性对求解结果有一定影响,但总体来看,采用TPPOA算法优化的削峰率结果较为平稳。
5 结论
针对复杂防洪系统的优化调度问题,本文提出了TPPOA算法,将POA算法分成三个层次,结合莱维飞行、模式搜索法等思路,进行调度决策更新,并利用并行技术加快计算速度。以赣江中下游防洪系统为研究实例,分别采用常规防洪调度规则、POA算法、TPPOA算法对“1961”“1973”和“1994”等200年一遇设计洪水进行优化防洪调度分析,研究结果表明:(1)TPPOA算法优化调度后的吉安、石上和外洲的洪峰流量相较其他调度方式更低,削峰效果更优;(2)TPPOA算法计算速度约为POA算法的3~7倍,计算速度更快,更为有效地利用计算资源。
总体而言,TPPOA算法计算速度快,优化解质量更高,相较传统POA算法具有一定优势,是复杂防洪系统优化调度的一种有效方法。

