河道特征对黑龙江上游冰坝生消影响
宋春山朱新宇韩红卫林立邦姚 植
(1. 东北农业大学 水利与土木工程学院,黑龙江 哈尔滨 150030;2. 黑龙江省寒区水资源与水利工程重点实验室,黑龙江 哈尔滨 150030)
1 研究背景
黑龙江上游河道具有典型山区性河流特征,河谷宽窄相间,河道比降变化急剧,支流较多,而部分河段具备平原河流特征,岛屿串珠相连,浅滩急流相间出现[1]。上游支流的额木尔河和石勒喀河河道流向均为西南流向东北,由低纬度流向高纬度,易造成上游开河早于下游,形成“武开江”[2]。“武开江”是在水力和热力共同作用下的机械开河,其特点是水势变化急剧,冰质坚硬,流冰多而集中,开河过程时间短,而“武开江”易导致冰坝形成[3-4]。春季开河(江)时,大量流冰块在特定河段,如河道束窄处、浅滩、急弯、连续弯道、尚未解冻冰盖的前缘等处受阻,冰块上爬下插,堆积形成冰凌阻水体,往往严重阻塞过水断面,使其上游水位显著壅高[5]。冰坝的形成是水流条件、冰量以及河流边界条件综合作用的结果,具体可归纳为:需要有集中而又有足够数量和强度的冰量,以及需要有阻止流冰顺利宣泄的河流边界条件,如河道束窄处、急弯或连续弯道、多分叉河段、未解体的冰盖等,当冰量集中时往往容易在这些地点发生堵塞,形成冰坝[6]。由于冰坝形成后持续时间较短,溃决时常有凌峰产生,且一般沿程递增,易对沿岸人民生命财产安全和水利工程等造成严重的破坏。
冰塞冰坝成灾机理主要通过历史冰凌洪水灾害的成因分析、原型观测及建立数学模型三个途径进行研究。Beltaos[7-9]描述和分析了开河期冰块堆积、冰坝形成、冰坝破坏的物理过程,提出当雍高水位超过封江水位高度与封冻期冰厚成一定比例时,冰盖会发生破裂产生流冰,这一特定的临界值为经验数值;Nafziger等[10]对冰塞消减水位变化和流凌运动进行观测分析,提出冰塞上游段融化所产生的波浪会引起冰塞的固结和释放;郭新蕾等[11-12]采用一维树状数学模型模拟调水工程等人工渠道冰盖发展过程。针对黑龙江干流冰塞冰坝情况,戴长雷等[13]统计分析黑龙江历史冰坝典型年建立相应经验公式对黑龙江冰坝进行预报;许丽玲等[14]选取与开江时间预报密切相关的气象因子,采用多元统计回归,建立黑龙江上游开江日期预报模型;王涛等[15-16]通过对降雪(雨)和气温分析建立了基于神经网络的冰坝预报模型;杨开林等[17]把冰、水、热动力学理论与爆破效果相结合,进行了冰盖下爆破预防冰坝的理论探究。目前对于冰坝的成因机理分析在热力条件及水力条件下的研究较多,在河道特征下的机理研究却较少,难以为防凌防汛提供高效服务[18]。
影响冰坝生消是多种因素共同作用的结果,主要因素有三点:热力条件、水力条件和河道特征。其中河道特征是基本不变的,而热力、水力条件是变化因素。本文在对黑龙江开江期冰坝成因机理研究的基础上,选择冰坝易发河段量化河道特征参数,开展有利于冰坝形成的热力与水力条件下,河道特征与冰坝生消的相关性研究。重点是根据河道比降、河道弯曲系数、河道缩窄系数建立河段冰坝形成概率回归方程,通过对比分析典型年的河道特征,建立适用于黑龙江上游段冰坝发生位置预报模型,为冰凌灾害预防提供可靠的理论依据。
2 研究区域概况
黑龙江位于我国最北端,是中俄界河,流域处于寒温带地区,东亚大陆季风气候特点突出,在极地大陆气团、蒙古高压控制下,冬季漫长,寒冷干燥,且上游冰坝区河道狭窄曲折,河口流路散乱,所以黑龙江上游冰坝多为河床阻塞型[19]。一般将雍水高度超过8.0 m的冰坝定义为严重冰坝[20],表1为黑龙江历史冰坝发生情况[13],1950—2013年以来的64年间,严重冰坝发生22次,发生概率为34.4%,平均3年发生一次较为严重冰坝,且发生地点不固定,持续时间一般为2~3 d,最长达到15 d[21]。其中1960年和1985年为特大冰坝,最大雍高水头分别达到13.56 m和12.60 m;冰坝中心加林达最高水位超过1958年特大洪水2.18 m和1.22 m;在黑龙江霍尔莫津段以上近千公里的江段形成冰坝超过17处,持续时间均超过10 d。

表1 黑龙江历史冰坝发生情况
3 研究方法
“武开河”期间河槽蓄水量充足,春季融冰期降雨量及气温等区间内变化反常,此时的热力和水力条件有利于冰坝形成,开江期流凌受河道特征影响,改变了沿程阻力及水流流速和方向,使冰凌产生堆积,形成冰坝[22]。黑龙江上游冰坝区段河道狭窄曲折,比降变化较大,使水流流态沿程分布不均[23],原因是河道流量和流速的大小是冰凌流动中的能量和动量源[24],因此流速变化反映了碎冰块在河道阻塞程度[25]。通过GPS追踪试验获取各河段水流平均流速,对其整理分析并与1960、1985、2000和2009年历史冰坝典型年黑龙江上游冰坝发生位置对比,筛选得出冰坝典型河段。影响发生位置的河道特征元素包括:河道长短、河网覆盖密度、河道比降、河道弯曲系数和河道突缩宽窄比等。结合黑龙江上游河道特点,选取河道比降、河道弯曲系数及河道突缩宽窄比作为模型变量,运用多元回归分析拟合方程[26],建立统计型冰坝发生概率与河道特征的变量关系。
3.1 GPS追踪试验设计 从河道流向及历年资料综合分析,针对现有冰坝预报模型的限制性,选择黑龙江上游漠河段至呼玛段作为试验地点。黑龙江漠河段江道两岸多山,狭窄,江河蜿蜒回转与山地之间,急滩深槽上下交错,比降大,水流流态紊乱,加之地理位置和气候条件综合作用,冰凌易卡塞形成冰坝[27]。根据历史资料记载,1964、1971、1973、2000和2009年漠河段均形成灾害性冰坝,出现了严重冰坝凌汛。选择漠河河段进行流冰期现场观测,在开江期向河道抛投GPS定位器,进行流速测量。流冰开始选取形态较好的大冰块,将组装好的GPS定位器投放至冰块上,GPS定位器使用“北斗+GPS+基站”的定位模式,平面定位精度10 m,工作温度-20~70 ℃;GPS定位器采用12 V2.6 Ah蓄电池供电,正常情况下可维持定位器7~10 d供电需求。GPS定位器在有手机信号的区域以间隔10 s传回时间、经纬度、速度、速度方向信息,支持手机监测GPS定位器实时位置,方便快速研判流冰动态。图1给出了6#GPS定位器(设备名称:goome-96488)在整个工作时间段内漂流历程示意图,经过5 d漂流约600 km。GPS定位器返回得到瞬时速度为所在冰块的瞬时速度,此时速度为点纵向流速。通过对瞬时流速进行积分计算得到河段实际长度,河段实际长度与时间的比值为该河段平均流速,从而进一步预测冰坝冰塞易发生位置,为数值模型的率定检验提供基础数据。分析冰坝形成与河道特征的关系,建立适合黑龙江上游开河期冰坝的河道特征模型,需要先确定典型河段。通过记录GPS反馈即时流速进行积分计算可得到相应河段开河期平均流速,河段平均流速的计算公式为:


图1 6#GPS定位器漂流历程示意

式中:v0为河段平均流速,m/s;L为河段实际长度,m;n为GPS反馈次数;Ti+1为GPS第i+1次反馈时间,s;Ti为GPS第i次反馈时间,s;vi为i~i+1时间段内流速,m/s。
3.2 河道特征模型基本方程根据各河段流速对比,判断阻塞情况及冰坝典型年各河段凌汛灾害程度,进而确定典型河段,并选取相应河段河道特征作为模型因子,建立适用于黑龙江上游冰坝预报模型。预报工作的关键是通过大量实测资料和观测数据建立河段冰坝发生概率与其河道特征相关变量之间的关系,根据冰凌灾害发生机理和黑龙江上游河道特征,建立了反映凌情因子的河段冰坝形成概率P,河段冰坝实际发生概率计算公式为:

式中:P为河段冰坝实际发生概率;y为河段发生冰坝年数;Y为实验样区发生冰坝年总数。模型中各河道特征因子计算公式如下,河道比降计算公式为:

式中:X1为河道比降;H1、H2分别为河段起点和终点的河床标高,m;L0为河段长度,m;J为河道比降系数。
河道弯曲系数计算公式为:

式中:X2为河道弯曲系数;L为河段两端点间沿河道中心轴线长度,m;I为河段两端点直线距离,m。
河道突缩宽窄比[28]计算公式为:

式中:X3为河道突缩宽窄比;B1为原河道断面宽度,m;B2为缩窄后河道断面宽度,m。
回归分析是确定2种或2种以上变量间相互依赖的定量关系的一种统计分析方法[29-30]。典型河段确定后选取各河段河道比降、河道弯曲系数、河道突缩宽窄比作为模型因子,运用回归方程拟合上述变量之间的关系,采用SPSS软件对数据进行预处理,结果显示当变量次数超过3次方时,模型相关系数增加较少,而误差增大10倍以上,因此建立冰坝比例因子同河道特征的二项式关系,模型基本方程的计算公式为:

式中P′为河段冰坝预测发生概率。
卡方检验是一种具有广泛用途的假设检验方法,属于非参数检验范畴,主要是比较两个及两个以上样本率的关联性分析[31-32]。将典型河段各河道特征模型因子带入式(7)所得特征方程,得到典型河段对应P′值,固定实验样区发生冰坝年总数为15年,设定一个阈值k(0,1),整理后统计四格表如表2所示。确认自由度为1,选择显著水平α=0.05,由卡方分布表找到临界值3.84。比较卡方值和阈值,当χ2 >3.84时,阈值k可作为判断冰坝是否发生的一个临界值,当χ2取得最大值时,对应的k即为最佳阈值。卡方值计算公式为:

式中:χ2为卡方值;a、b、c、d代表统计四格表中4个格子中样本的频数;N为总次数,即a、b、c、d频数之和。

表2 典型河段冰坝发生统计
3.3 模型验证为比较河道特征模型模拟效果,采用经验统计法预报结果进行对比。黑龙江冰坝预报目前采用的经验统计学模型为成因几率统计法[13],发生率计算公式为:

式中:P″为n个冰坝形成影响因子的平均几率;P总为影响因子几率和;n为影响因子个数;Pn为第n个影响因子几率。
为进一步验证模型最佳回归方程可靠性,采用均方根误差(RMSE)来测量模拟和实际值的一致性,整理得出模型效率系数(EF)描述实际数据趋势,计算公式如下[33]:

式中:Fs为实际值;Fo为模型预测值;n为模型选取河段个数。

式中:Oi为模型预测值;Si为河道模拟量;O0为模型输出量平均值。
3.4 数据来源及处理漠河段GPS追踪试验,所得GPS反馈数据采用EXCEL程序进行数据计算;并采用Origin9.0软件进行作图。国家科技基础平台建设项目“地球系统科学数据中心共享平台(www.geo⁃data.cn)”为学科积累大量河道资料并广泛应用于冰灾害研究中[15],模型所需要的河道资料主要来自国家地球系统科学数据中心和典型年冰坝情况历史文献[13]。采用中国科学院计算机网络信息中心国际科学数据镜像网站(http://www.gscloud.cn)提供的空间分辨率为30 m的ASTERGDEM,作为获取地形因子的数据。采用OMAP软件及CAD软件对河道特征元素进行测绘整理;采用SAS9.2软件进行方程模拟及模型检验;采用MATLAB软件对不同河道特征因素进行耦合效应分析;采用SPSS19.0程序进行变量相关性分析和显著性分析。
4 结果与分析
4.1 典型河段选取结果漠河段GPS追踪试验共投放20枚GPS定位器,2019年4月28日在洛古河水文断面投放一枚,位移监测显现2019年4月30日03∶30左右洛古河断面开始流冰。2019年4月30日11∶10北极村观测断面,大块浮冰开始缓慢启动开始流动。北极村观测断面投放19枚GPS定位器,其中6枚未通过北红村,13枚通过兴安镇,其中的9枚停留在兴安镇与下地营子(二十四站附近),1枚停留在桂花站附近,3枚通过呼玛县,并最终停留在三卡乡附近。其中6#GPS定位器(设备名称:goome-96488)在河道中漂流约600 km。
GPS通过各河段平均流速情况如图2所示,2019年黑龙江开河期上游各江段平均流速呈现先减小后增大再减小的趋势,反映了黑龙江河流流向及地理位置制约着冰坝形成的动力条件。顺直江段平均流速为9 km/h,依西肯段平均流速最小为4.2 km/h,较顺直段偏低53%。通过流速对比可知,流冰行至此类河段流速减慢,容易发生堵塞。查阅1960、1971、1985、2000和2009年特大冰坝文献记录选取黑龙江上游易发生河段进行综合比较,开河期平均流速低于漠河段流速的江段在典型年均有冰坝形成。其中漠河段平均流速为顺直段平均流速的71%,故以低于顺直段平均流速29%为界,小于或等于此临界值时开河期冰盖破裂的碎冰块流至此类河段就会发生堵塞,反之,则不会发生阻塞。因此选取黑龙江上游漠河段、乌苏里段、加林达段、古城岛段、马伦段、开库康段、双合站段、依西肯段、欧浦段、正棋段、金山段、呼玛段12处江段的河道特征因素作为典型河段。

图2 GPS行至各河段平均流速(注:不同子母间表示处理间差异显著(P<0.05))
4.2 河道特征的多元回归分析河道特征的三个指标对冰坝形成的作用力各不同,存在定量指标权量不一的情况。黑龙江上游冰坝易发河段河道特征系数统计表如表3所示。将表3中河道比降、河道弯曲系数和河道突缩宽窄比参数输入到冰坝河道特征模型中,并采用多元回归对参数进行调整[34]。建立在式(7)回归方程基础上,计算典型河段冰坝预测发生概率同河道比降、河道弯曲系数及河道突缩宽窄比的纯二项式和交差二项式关系式如下:

式中:P′1为纯二项式下河段冰坝预测发生概率;P′2为交叉二项式下河段冰坝预测发生概率;X1为河道比降;X2为河道弯曲系数;X3为河道突缩宽窄比。
采用相关系数(R2)、显著系数(P-value)比较纯二项式与交差二项式的拟合优度,从而选出最佳,式(12)和式(13)预报结果和实际结果的可决系数和显著系数见表4。
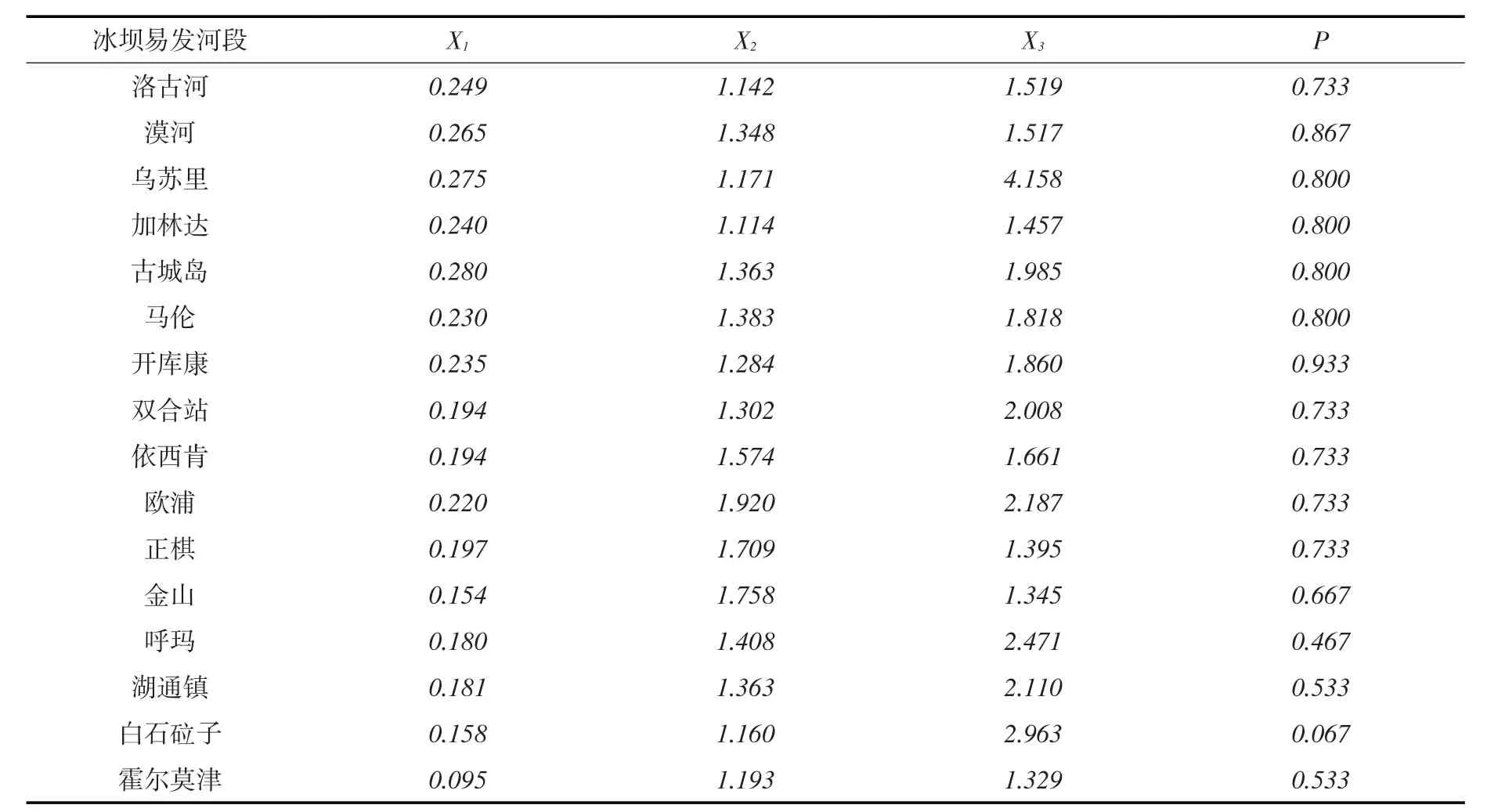
表3 黑龙江上游冰坝易发河段河道特征系数统计

表4 纯二项式与交差二项式评定对比
基于河道比降、河道弯曲系数和河道突缩宽窄比的河段冰坝发生概率关系式(12)和式(13)中,相关系数和显著系数交差二项式高于纯二项式,因此采用交差二项式(13)作为模型计算公式。将河段比降、河段实际长度、河段的直线长度、河道断面宽度、缩窄后河道断面宽度代入式(12)得到黑龙江上游河道特征方程如下:

式中:L为河段实际长度,m;B1为原河道断面宽度,m;B2为缩窄后河道断面宽度,m;I为河段的直线长度,m。
基于多元回归的黑龙江上游冰坝河道特征计算模型预报黑龙江冰坝发生情况,GPS追踪试验及1960、1985、2000和2009年冰坝发生河段河道特征数据作为模型的学习数据,将典型河段各河道特征模型因子带入所得特征方程式(13)中,得到典型河段对应P′值,固定实验样区发生冰坝年总数为15年,由表5可知当阈值k=0.69时,所求得卡方值最大为7.40,大于临界值3.84,故选取最佳阈值0.69作为发生冰坝的判别,大于或等于此临界值就发生冰坝,反之,则不会发生。

表5 卡方值统计
4.3 冰坝发生情况预报由3.2节所得最佳阈值0.69判别冰坝发生情况,以1971年数据作为模型基础数据,通过河道特征模型(式(14))预报该年典型河段冰坝发生位置的概率。将典型河段河道特征系数作为基础数据运用几率分析法(式(9))预报1971年各河段冰坝发生情况。河道特征模型预报结果和经验统计模型预报结果如表6所示。
分析1958—2010年冰坝成因发生率,因子平均发生率为41%,故以41%作为标准判断冰坝是否发生的依据。由表6可知预报1971年冰坝发生位置情况,河道特征模型预报错误2站,几率分析法预报错误5站,河道特征模型预报精度为85%,统计学模型预报精度为62%。金山段和呼玛段河道模型未预报冰坝发生,因为金山段河道比降较为平缓,呼玛段河道弯曲系数小于1.5,属顺直型河道,而1971年黑龙江上游,气温变化急剧,在漠河段至呼玛段区间有30~40 mm的强降雨过程,雨雪径流汇入河槽,促使上游干支流解冻开河,造成了以水力条件作用为主的“武开江”。表6对比结果表明,经验统计学模型预报准确率较低,对于主要影响因素要求较高,河道特征模型改进了传统的计算方法,构建具有一定指示意义的因子,使冰凌灾害的计算和预报具有明确的物理成因,能较好地反映冰坝发生的实际变化规律,为进一步建立较为合适的冰凌灾害预报方案提供了科学支撑。
4.4 各河道特征耦合效应分析为探究各河道特征之间的耦合效应,利用MATLAB对式(13)做二因素交互作用三维模型图。图3表示河道比降、河道弯曲系数和河道突缩宽窄比对冰坝生消的影响。由图3(b)可知,固定河道突缩宽窄比为3.0时,随着河道比降及河道弯曲系数增大,冰坝生成概率增加,在河道比降区间为2‰~3‰时增幅明显加强,由图3(c)可知,在河道弯曲系数区间为2.0~3.0时,随着河道比降和河道突缩宽窄比增大,冰坝生成概率增幅明显,由图3(d)可知,固定河道比降为2‰时,随着河道弯曲系数及河道突缩宽窄比增大冰坝发生概率增幅缓慢;固定河道比降为3‰时,随着河道弯曲系数和河道突缩宽窄比增大,冰坝发生概率增幅明显,这说明河道比降在河道特征三要素中对冰坝形成影响最大。在模型拟合范围内,河道比降及河道弯曲系数所引起的冰坝发生概率变化幅度大于河道突缩宽窄比,所以在有利于冰坝形成的热力和水力条件下,河道突缩宽窄比对冰坝形成影响最小,这可能是因为黑龙江上游突缩系数较大河段多位于高纬度,其源头额尔古纳河和石勒喀河两大支流从西南流向东北,由低纬度向高纬度流动,纬度相差7°,纬距700 km,造成开河期受热不同,致使解冻期河源及上游低纬度处地段先受热解冻开河,具备了“倒开江”的先决条件,易造成冰块堆积,壅冰成坝[6,22]。
4.5 精度评价利用均方根误差和模型效率系数模拟预报值和实际值之间的仿真能力和适用性,将4.3节所得预报值与实际值代入式(10)和式(11),得出RMSE值为0.02,EF值为0.98。参考《水文情报预报规范》(GB/T22482-2008)[35],评定结果属于甲等预报方案。说明基于多元回归的河道特征冰坝预报模型能够较好的模拟武开河或倒开江条件下的黑龙江上游各河段冰坝发生概率。通过对冰坝实际发生概率与预测发生概率进行比较,对模型进行了标定和验证。实际值与预测值对比如图4所示。除个体差异外,模型的仿真结果与实际发生概率结果吻合较好。回归分析表明,回归相关系数(R2)为0.83,回归方程斜率为0.86。预测值与实际值呈极显著相关(P<0.001)。
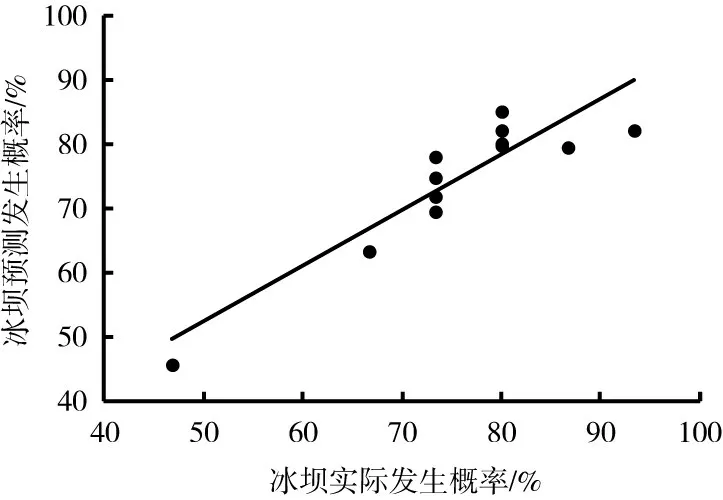
图4 冰坝预测发生概率与冰坝实际发生概率
5 讨论
针对黑龙江上游冰坝凌汛灾害,张义夫等[2]研究表明河道形态除了能够改变水流而影响冰情变化外,它还对冰凌具有卡塞作用。本文研究表明,冰坝形成与河道比降、河道弯曲系数和河道突缩宽窄比具有明显的相关性。黑龙江上游漠河至呼玛段间上河段与下河段比降之比为1.3~5.0,且相邻河段河道沿程变化急剧,为冰坝多发段[36]。Wuebben等[37]研究结果表明河道的自然构造特征会对冰坝的位置产生影响,水力坡度是促进冰坝形成的一个重要因素,本文观测结果也证实了这一点。冰坝形成最常见的位置是在河道比降由陡变化到缓的区域,如1960年冰坝凌汛灾害严重的加林达至古城岛段及新街基江段,其水面比降比相邻江段明显偏小,是由于重力作为流冰的驱动力,当河中碎冰块流至缓坡区域,阻力增大,水流动力逐渐减弱,冰块停止移动开始堆积,并减小了河道过水能力,最终形成冰坝,Urroz[38]也得出相似结论。黑龙江的上游段属于典型的山区性河流,江道弯曲呈L型、S型或者Ω型,部分河段甚至会出现大于90°的弯角转折,其中上中游弯曲系数均值为1.20,但在局部河段曲折系数出现高值跳跃点[39],在所研究区域的欧浦段河道弯曲系数达到为1.92。河道中的弯道对冰坝的形成产生积极影响,通过迫使流冰改变运动方向,并使冰块撞击外侧河岸,因此弯道常常被列为冰坝的起源地[40]。如黑龙江上游下地江段营子岛以下江段,槽线呈U形变化,连崟江段槽线呈双S形变化,当水流通过这些弯曲江段时,会产生附加离心作用,形成断面环流,易于形成冰坝[13]。随着河道断面的宽窄比的增大,水流进入河道突缩段后流速会越来越快,河道宽窄比越大水流在流经河道突缩段前后的流态更紊乱[28]。孙延锋等[24]研究表明当流凌行至束狭江段,由于水域的骤然收缩引起流冰的过分集中,易造成卡冰堵塞,这与本文的研究结果一致。黑龙江上游河谷宽窄程度相间,河道岸线非常的不规则,上游冰坝易发河段平均河道突缩宽窄比为1.98。开河期流凌行至主河道突缩段时,局部阻力损失增大,流态紊乱,易形成巨大的冰堆积体,引起过水能力不均,利于冰坝的产生。黑龙江上游的河道特征冰坝预报模型是建立“武开江”或“倒开江”有利于冰坝形成的水力和热力条件下,将各河段河道特征系数输入特征方程,预测各河段形成冰坝的概率,可初步确定冰坝发生位置,为黑龙江上游冰情凌汛预警工作提供一定的理论贡献。
6 结论
以黑龙江上游冰坝易发河段为研究对象,从河道特征角度入手对冰坝生消演变进行研究。得到结果如下:(1)分析对比典型河段历史冰坝发生位置,得出流域地势越陡峭,河道比降区间为2‰~3‰,河道弯曲系数处于2.0~3.0之间,河道突缩宽窄比超过3.0的河段,在“武开江”下越容易形成冰坝。(2)GPS追踪试验所得流速变化反馈开江期各河段流冰阻塞情况,与冰坝易发河段契合良好。冰坝的形成及演变极为复杂,将所选取的典型河段河道比降、河道弯曲系数和河道突缩宽窄比作为模型因子输入到冰坝预报模型中,并采用多元回归方法对参数进行优化,建立黑龙江上游河道特征方程,计算所得最佳阈值0.69作为发生冰坝的判别标准,大于或等于此临界值会发生冰坝,反之,则不会发生。(3)通过模拟上游各河段河道因素,预报冰坝在某河段的发生概率,模拟结果对比历史典型年凌汛情况吻合较好,验算得出模型均方根误差为0.02、模型效率系数为0.98。与传统经验统计冰坝预报模型比较,本研究以形成冰坝的动力条件为前提,建立了基于河道特征的黑龙江冰坝回归模型,预报精度为85%。根据《水文情报预报规范》(GB/T22482-2008),模型较为准确的预报了黑龙江上游不同河段开河期冰坝发生概率。
冰坝的发展机制是极其复杂的,概括来说主要影响因素有三点:河道特征、热力条件和水力条件,其中河道特征为固定因素,而热力与水力条件是变化因素,二者的本质存在内在联系,同时相互作用、互为转化。对于自然条件下,河床总是处在不断的变化过程中,在河流上修建水工建筑物后,会引起上下游河势的变化,在接下来的研究中应注重综合考虑多种水文因素与河道特征对冰坝形成的交互作用,提升技术设备条件。冰坝形成过程十分复杂,故对于冰坝形成机理有待进一步研究。

