超固结非饱和土的弹塑性双面模型

李潇旋，李 涛，李 舰

（北京交通大学 土木建筑工程学院，北京 100044）

1 研究背景

非饱和土在自然界中分布广泛，具有复杂的物理和力学特性。在地球表层的实际工程中，如高速公路和铁路路基工程、隧道工程及边坡海岸工程等，由于超载预压地基处理工艺以及卸荷、再加荷等循环加载作用，非饱和土大部分处于超固结状态。超固结非饱和土表现出应变软化和剪胀、高峰值应力比以及应力路径相关性，常规临界状态模型无法合理地描述这些特性。因此，研究超固结非饱和土的力学特性和本构关系具有重要的理论价值和工程意义。

国内外学者对正常固结和弱超固结非饱和土进行了大量的理论和试验研究，在本构模型方面取得了许多有益的成果。Alonso等[1]基于不同吸力下非饱和土体积和应力的变化关系试验结果，在临界状态土力学框架内最早提出非饱和土的弹塑性模型，被称为BBM（Barcelona Basic Model）模型。Wheeler[2]修正了BBM模型中的LC屈服面，提出了改进的BBM模型用于描述非饱和高岭土的基本力学性质。Sun等[3-4]基于SMP破坏准则，采用变换应力法推导了非饱和土的三维弹塑性本构关系，并用压实高岭土的试验结果进行了验证。后来，Wheeler等[5]考虑饱和度影响，采用Bishop应力和修正的基质吸力建立了较完整的水力-力学耦合模型。缪林昌[6]引用骨架应力的概念推导了LC屈服面的函数和硬化规律，建立了体应变引起饱和度变化的关系式。Sheng等[7-8]指出在非饱和土土-水特性中饱和度不仅与吸力有关，而且还与体应变有关，并据此建立了水力-力学完全耦合的弹塑性本构模型。蔡国庆等[9]以非饱和细砂为研究对象，运用等速率单轴拉伸方法开展了不同干密度和含水率条件下的非饱和土抗拉强度试验研究，探讨了土体抗拉强度随干密度和含水率的变化规律。在考虑循环荷载作用方面，Li和Meissner[10-11]将Masing准则推广到多维应力空间，提出了一种新型塑性硬化准则（以下简称Li-Meissner硬化准则），它采用径向映射法则和可移动的记忆中心，通过边界面和加载面在应力空间中的演化来反映循环加载过程中材料的循环塑性特征。基于该准则建立的饱和黏性土的弹塑性双面模型可以较好地模拟循环荷载作用下饱和黏性土的力学特性。李潇旋等[12-13]基于BBM和Li-Meissner硬化准则，建立了循环荷载下非饱和土的弹塑性双面模型，其中考虑了土体结构性的影响。孙德安和吴波[14]使用吸力可控或可测的非饱和土振动三轴试验仪，对非饱和及饱和粉土进行动态加载试验，在不同净围压应力、不同初始含水率的条件下，得到了非饱和及饱和粉土试样的动应力应变骨架曲线、动弹性模量和阻尼比，并量测了试样吸力。

以上模型均针对正常固结非饱和土进行研究，而有关超固结非饱和土在静态及循环荷载作用下的力学特性的研究近年已有所报道。徐连民等[15]在修正剑桥模型的屈服函数中引入描述超固结黏土变形和强度特性的状态量，进一步改进修正的剑桥模型以应用于超固结土的变形特性研究，并给出该状态量的演化规则。Estabragh等[16-17]针对超固结非饱和粉土在控制吸力条件下进行了系列三轴剪切试验，探索了吸力和超固结比的影响。Wu等[18]通过一系列固结排气不排水的常含水量（CW）三轴试验，分析了吸力和超固结比在超固结非饱和粉土的水力-力学耦合特性中的作用。姚仰平等[19]采用抛物线近似代替Hvorslev线，该抛物线将零拉应力线与Hvorslev线表达成一条统一的剪切强度包络线，提出了基于改进Hvorslev线的超固结土模型。随后，Yao等[20]、姚仰平等[21]将BBM与超固结土的UH模型相结合，建立了超固结非饱和土的UH模型，它们能够反映超固结非饱和土的硬化、软化、剪缩、剪胀特性和不同应力路径对超固结非饱和土变形特性的影响；还通过基于SMP准则的变换应力三维化方法将模型扩展到三维应力空间。李吴刚和杨庆[22-23]利用下加载面理论，将超固结的影响加入现有的水力-力学耦合模型中，给出了该超固结非饱和土水力-力学耦合模型的隐式积分算法和本构模型的一致切线模量，并对该算法进行了验证。

本文基于非饱和土经典BBM模型和可描述循环荷载下饱和与非饱和土循环塑性的Li-Meissner硬化准则，首先通过各向等压卸载引入超固结特性，尝试建立一个描述常吸力下超固结非饱和黏性土静态及动态力学特性的弹塑性双面模型；然后采用相关静态试验成果验证所建模型的合理性；最后，对超固结非饱和黏性土的循环塑性特征进行预测。本文所建模型可为掘进与非饱和土有关的实际工程问题提供理论基础。

2 超固结非饱和黏土双面模型的建立

2.1 边界面和加载面方程根据BBM模型[1]和弹塑性双面模型[10]理论，在循环荷载作用下，边界面和加载面在p-q-s应力空间中按照一定的规则进行演化，来表征非饱和土的动态力学特性。在演化过程中，不同吸力值对应的边界面以及加载面的演化规律是一致的。常吸力条件下应力路径只在某恒定吸力的p-q平面上发生变化，为了表达的方便和简洁，可用该p-q平面上边界面和加载面椭圆的演化规律，即边界面和加载面的常吸力截面的演化规律来反映p-q-s应力空间中三维边界面和加载面的演化规律[2]，因此超固结非饱和黏土的边界面方程可写为：

式中：m为循环加载过程中的独立加卸载事件，如m=0为初始固结加载，m=1为等向卸载过程，m=2为第一次剪切加载，余类推；分别为第m次加载过程中边界面在应力空间中圆心的坐标和p方向长半轴（图1）；M为临界状态线（CSL）的斜率。

加载面与边界面几何相似，方程可以写为：

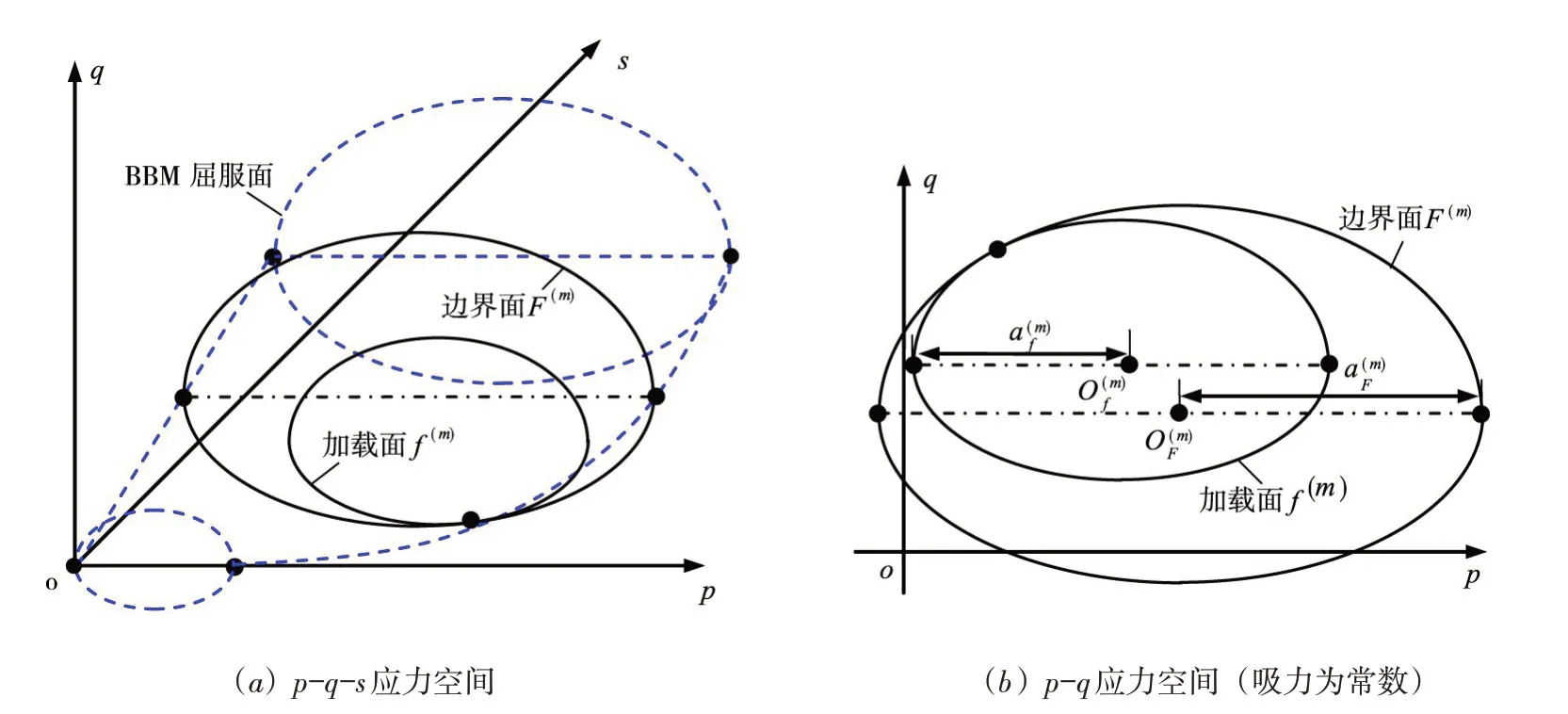
图1 非饱和土的边界面和加载面

2.2 非饱和土的超固结特性非饱和土在固结完成后，如果遇到等向卸载作用，则在卸载完成后非饱和土具有一定的超固结特性，超固结比OCR与卸载完成后的围压有关。

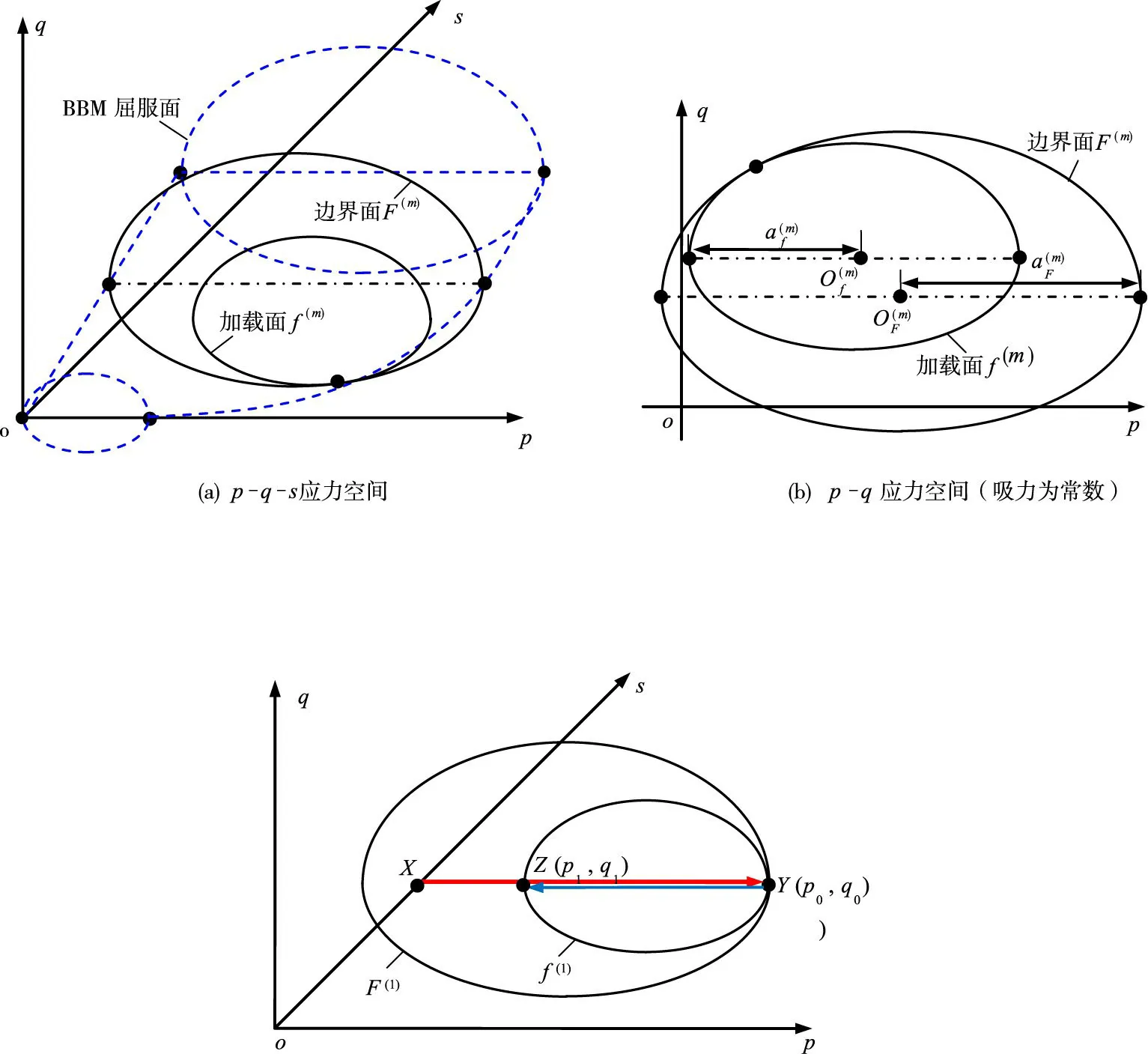
图2 应力空间中的超固结非饱和土（s=sc）

如图2所示，吸力平衡至X点s=sc（sc为常数）后，在常吸力条件下，非饱和土首先进行各向等压加载，固结至Y点，然后再各向等压卸载至Z点，有：

若卸载后的围压越小，则非饱和土的超固结比越大，具有的超固结特性就越强。

2.3 模型的塑性硬化准则模型采用的Li-Meissner塑性硬化准则[10]的主要特点如下：

（1）将应力空间中应力路径转折点（区分循环加卸载）定义为记忆中心，边界面与加载面几何相似并始终在记忆中心相切。

（2）在加载事件中，通过加载面膨胀描述该次加载事件，同时边界面因新的塑性体积应变而变化。当加卸载转换时应力路径发生突然转折，该应力转折点成为新的记忆中心，出现新的加载面描述新的加载事件。

（3）为了保证变形的连续性，每当记忆中心移动到新的位置时，边界面也随之发生移动，与新的加载面相切于新的记忆中心，且初始大小与上一次事件结束后边界面的大小一样。

根据以上特点，本模型塑性变形计算所需的塑性模量取决于加载点到映射点的距离和边界面映射点的塑性模量，而边界面的演化取决于塑性体积应变（塑性硬化参数），即边界面的大小不仅代表了塑性加载的历史，同时也影响了加载时塑性应变的计算。因此，模型要求在新加载事件开始的瞬间，土体不仅仍具有上一次事件结束时的塑性加载历史，而且还要保证边界面和加载面之间原有的几何构架，否则将不能保证塑性变形计算的连续性。

图3 加载面和边界面演化示意

常吸力条件下，初始各向等压固结过程（图3（a））通过F（0）来描述，记忆中心为X点。固结完成后，开始各向等压卸载（图3（b）），此时应力路径发生转折，Y点成为新的记忆中心。应力路径到达Z点时，卸载完成，非饱和土具有超固结特性。当应力点在Z点发生转折并指向A点（图3（c）），应力路径发生转折，Z点成为新的记忆中心，用f（2）和F（2）来描述加载事件ZA。当应力点在A点发生转折并指向B点（图3（d）），应力路径为AB，记忆中心移动到A点，产生新的f（3）和F（3）。

上述硬化法则的优点是把一个连续的加卸载过程分解为独立的加载事件，只用两个面的演化来描述一个加载事件，提高了弹塑性双面模型的模拟能力。

2.4 弹塑性增量本构关系弹性应变增量为：

式中：K为弹性体积模量；G为弹性剪切模量，有：

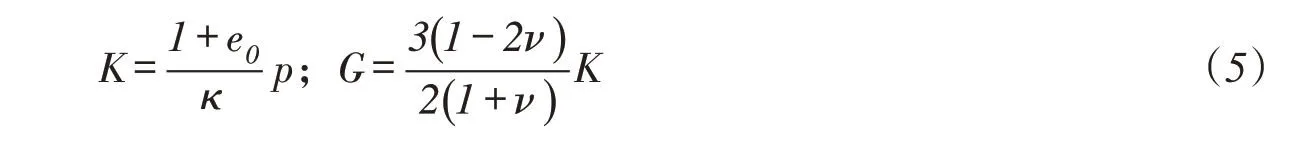
当前应力点的塑性应变增量由加载面来表示。采用相关联流动法则，塑性应变增量为：

式中：为Macauley运算符，当且仅当内部参量为正时取值；ψ为修正系数，由流动法则在侧压力系数K0加载时预估的侧应变为零这个条件来选择；n为当前应力点外法线的单位矢量，加载面上P点处外法线单位矢量在坐标轴方向的分量为：

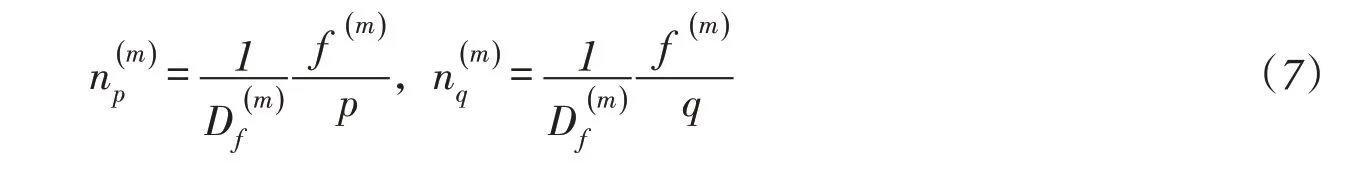
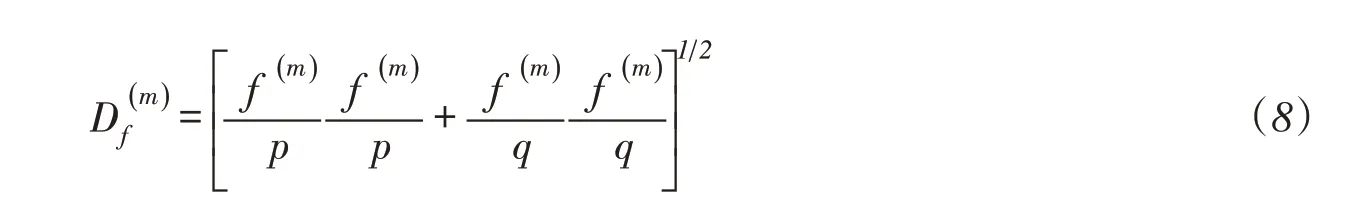
式中：hm为当前应力点的模量。

同理，因边界面和加载面相似，将上述方程中的小写字母f和n换成大写字母F和N即可得边界面上相关公式。

2.5 模型的演化规律在各向等压固结过程（m=0）中，边界面F（0）和加载面f（0）重合（见图4）。

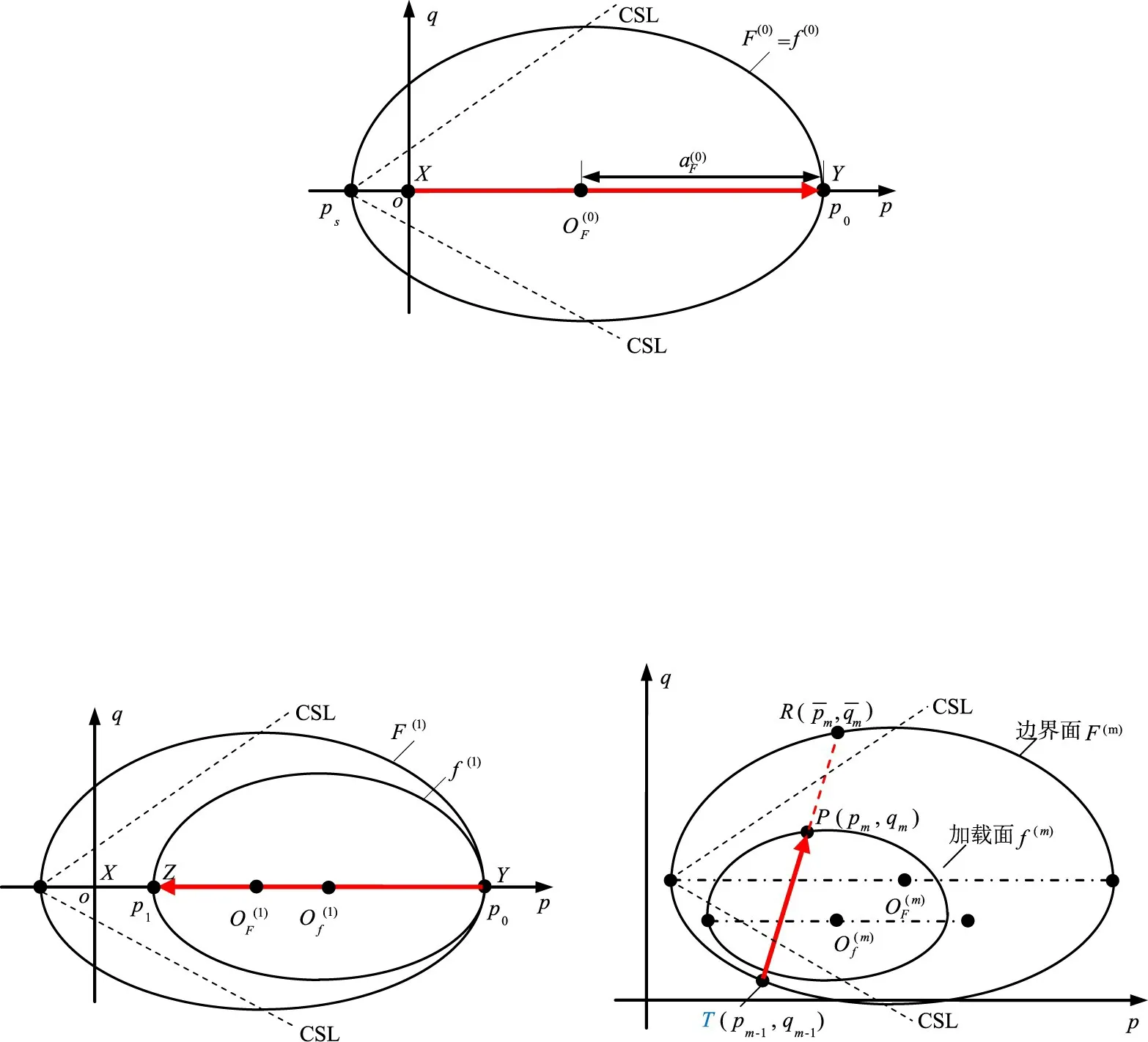
图4 各向等压固结过程中的边界面和加载面

F（0）的长半轴和中心坐标分别为：

式中：p0为常吸力s=sc（sc为常数）下非饱和土的固结应力；ps为因吸力存在引起的黏聚力，由BBM可得：

在各向等压卸载过程（m=1）中，Y点成为新的记忆中心，加载面f（1）围绕Y点进行演化，边界面F（1）随着塑性变形的产生而变化（见图5）。

边界面F（1）初始大小和位置与固结完成后的边界面F（0）一样。由加载面和边界面之间的几何关系，加载面f（1）的大小和位置可写为：

对于第m次加载，边界面和加载面在记忆中心T点相切，P为当前应力点，R为边界面上的共轭点（见图6）。

由于边界面代表着应力历史，只跟塑性体应变有关，参照饱和黏土剑桥模型的硬化法则，在某吸力状态下有：

图5 各向等压卸载过程中的边界面和加载面

图6 第m次加载时的边界面和加载面

联立固结完成后m=0的表达式可推导出边界面长半轴计算公式：

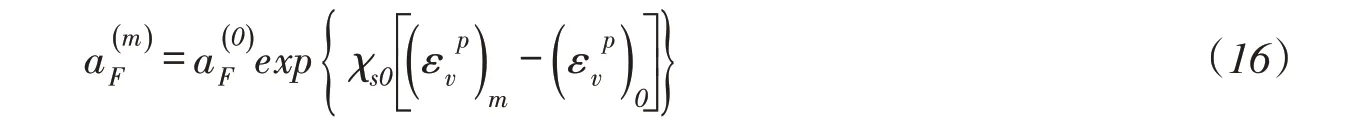
由于加载面和边界面始终在记忆中心相切，根据二者之间的几何关系可推导出其半径和圆心的坐标如下：

2.6 塑性硬化模量已知边界面的一致性条件为：

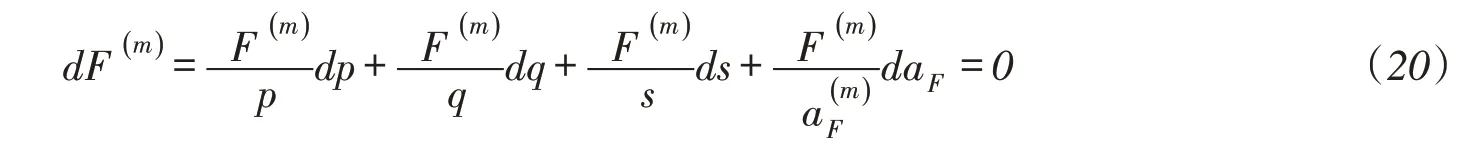
据此，可以推导出边界面上共轭点处的塑性硬化模量为：

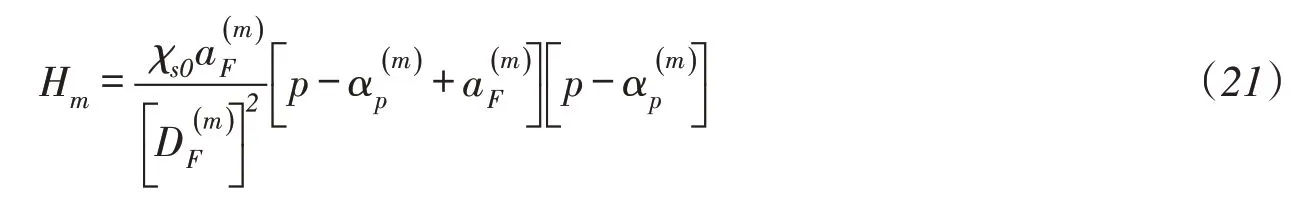
加载面上当前应力点的塑性硬化模量可由边界面上共轭点的模量以及二者之间的距离插值求出，本模型采用以下插值函数[24]：

式中：HR为边界面上共轭点的塑性模量，可由式（21）联立模型的演化规律进行计算；HM为记忆中心点的塑性模量，与土的性质和加载条件有关；δ、δ0分别为当前应力点和记忆中心到共轭点的距离，有当d=d0时，当前应力点位于记忆中心，hm=HM，当d=0时，当前应力点位于共轭点，hm=HR。参数γ定义为：

式中：b和γb为常数，取决于土的初始孔隙比、静强度和动剪应力幅值等因素；εQ为整个加载过程中产生的有效塑性应变，

3 模型的静态加载试验验证

Estabragh等[16]针对超固结非饱和粉土在控制吸力条件下进行了系列各向等向压缩和三轴剪切试验。试验首先将试样平衡至不同的吸力（0，100，200，300 kPa），分别控制吸力不变将试样各向等向压缩至相同的前期固结压力550 kPa，然后分别各向等向回弹至不同的应力（50，200，400 kPa），以获得不同的超固结比OCR，最后再进行吸力不变的常规三轴剪切试验。试验的基本条件见表1。本文通过控制吸力各向等向压缩试验、控制吸力和净应力的剪切试验来拟合参数，标定过程如下：根据文献[16]中各向同性压缩试验的结果，可得λ（0）=0.078，λ（200）=0.071和λ（300）=0.055，带入λ（s）=λ（0）[r+（1-r）exp（-βs）]可求出β=0.001 kPa-1，r=0.06；根据文献[16]中饱和状态临界状态线可求出M=1.26；因M不随吸力的变化而改变，可通过q/（p+ks）=M求出k=0.2；根据饱和状态的压缩和回弹曲线可求出p 0=50 kPa，κ=0.01；初始孔隙比取平均值0.705；泊松比为0；参考应力pc取10 kPa。本文模型通过FORTRAN语言编程，在VS（Visual Studio）2012+IVF（Intel Visual FORTRAN）2013环境下编译。模型采用的参数取值如下：M=1.26，k=0.2，λ（0）=0.078，e0=0.705，ν=0，κ=0.01，β=0.001 kPa-1，r=0.06，p 0=50 kPa，pc=10 kPa。模型预测与试验结果对比如图7。

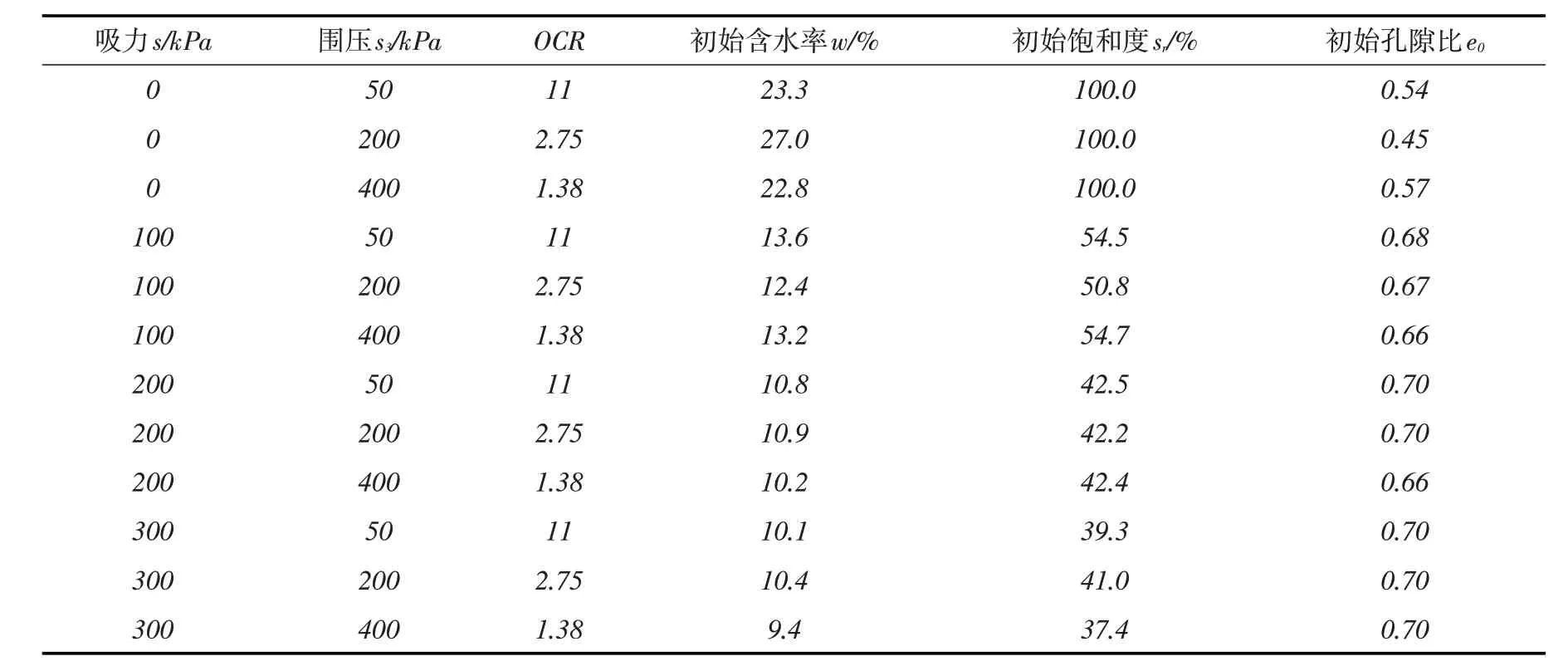
表1 常规三轴试验

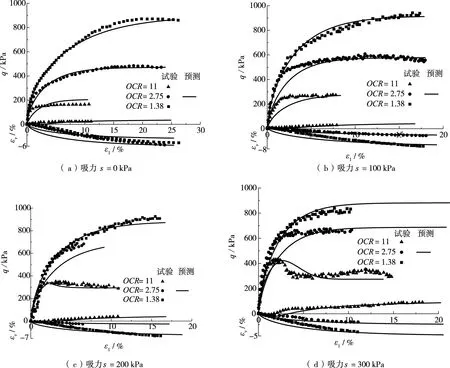
图7 预测结果与试验数据对比图

从图7可以看出模型预测结果与试验结果吻合较好。OCR值较小的非饱和土（轻超固结土）试样在剪切过程中应力-应变曲线没有明显的峰值点，一直处于硬化状态，体积也不断的减小（图7（a）（b））；具有较高OCR值的非饱和土（重超固结土）试样的应力-应变曲线有明显的峰值强度，到达峰值强度后出现了软化行为，体积随着加载首先收缩，随后又发生剪胀（图7（c）（d））；这说明本文模型能够合理反映静态加载条件下超固结非饱和黏性土的应变软化和剪胀等主要力学特性。

相同吸力条件下，OCR值越高，考虑围压后的应力比-应变峰值强度越高，应变软化越明显，说明重超固结土相对于轻超固结土和正常超固结土具有较高的强度；OCR值一定时，吸力越大，试样的峰值强度越高，应变软化越明显，说明吸力增加也可以提高超固结非饱和土的强度。

4 模型的动态加载试验预测

由于目前非饱和土吸力测试的技术达不到动力试验的要求，加之非饱和土本身物理力学性质的复杂性，有关超固结非饱和土在循环荷载作用下动态力学特性的试验研究少见报道。为了探索吸力和超固结比OCR对超固结非饱和土动态力学特性的影响，采用本文模型对超固结非饱和黏土在常吸力循环荷载下的动态力学特性进行预测，以了解超固结非饱和土的动态力学特性。预测采用上节静态加载试验的材料及非饱和状态相关参数，循环加载相关的参数中，b表征土体的初始刚度，并与其成正比；γb表征土体的极限强度，并与其成反比。b和γb可通过土体的循环三轴试验结果求出，它们与土体的初始状态、静强度和加载条件等因素有关。本文取b=13.4，γb =12.7，动应力幅值为250 kPa。受限于篇幅，仅采取吸力s=100 kPa和s=300 kPa，OCR=1.38和OCR=11共4种工况进行预测，预测结果如图8—9所示。

从图8和图9可以看出，循环荷载下超固结非饱和土的应力-应变曲线出现了滞回现象，较好地反映了土的循环塑性特性，表明本文提出的模型是可行的。在超固结比OCR一定时，吸力越大，土体达到稳定时累积应变越小，说明吸力提高了土体的强度。而吸力一定时，超固结比OCR越大，土体达到稳定时累积应变越小，说明超固结作用也可以提高土体强度。因此，非饱和土路基在经过超载预压地基处理工艺变成超固结状态后，路基土强度提高，沉降减少。

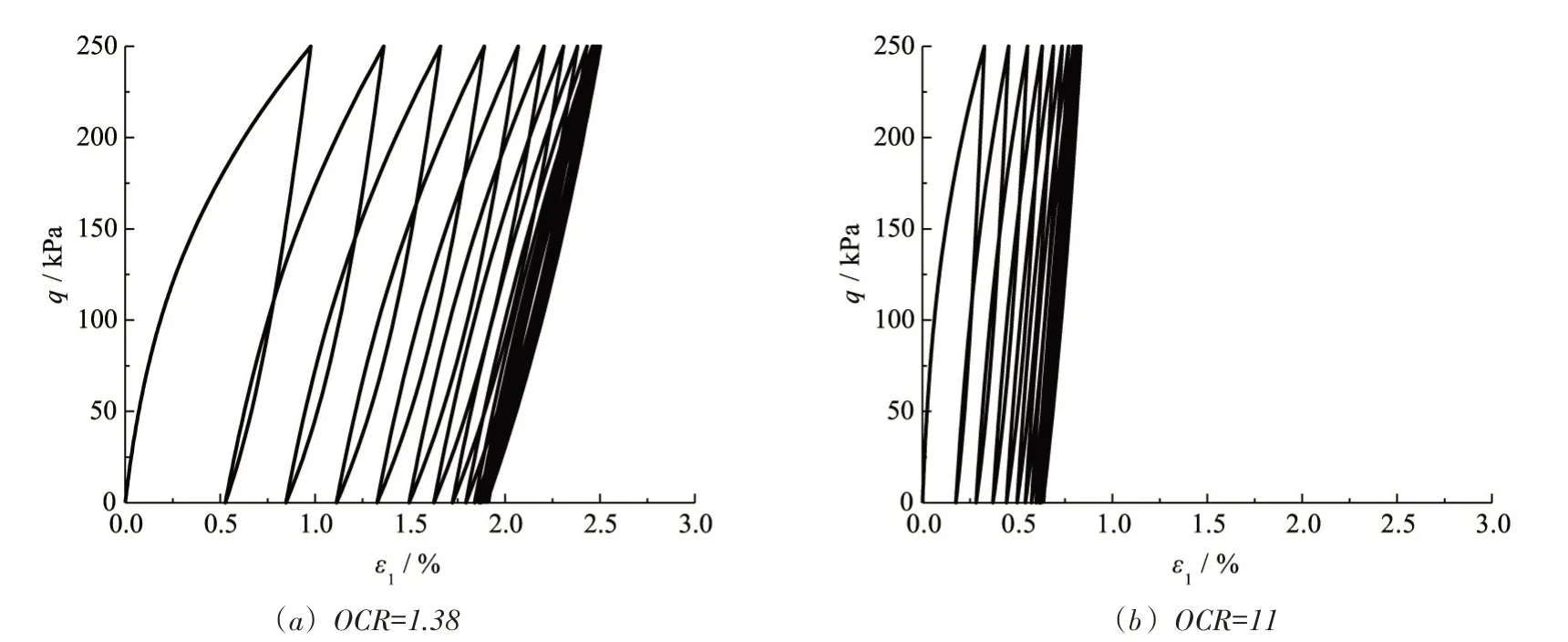
图8 循环三轴试验模型预测结果（s=100kPa）

图9 循环三轴试验模型预测结果（s=300kPa）

随着循环加载的进行，滞回圈的面积越来越小，加载过程和卸载过程的曲线趋于重合，最终处在一个循环稳定状态，说明在循环荷载的持续作用下，土体的变形逐渐以弹性变形为主，塑性特征越来越不明显。

5 结论

（1）将一个连续的循环加卸载过程分解为独立的加载事件，只用两个面的演化来描述一个加载事件，提高了弹塑性双面模型模拟非饱和土动态力学特性的能力。

（2）通过与控制吸力常规三轴静态试验结果的对比以及对动态特性的预测分析，表明本文模型可以合理描述超固结非饱和土的静态和动态力学特性。

（3）超固结比OCR和吸力均能在一定范围内提高超固结非饱和土的强度，从而减小超固结非饱和土路基的沉降。

（4）所建模型仅考虑了应力-应变关系，具有一定的局限性，后续需要对受荷过程中水力特性及水力-力学耦合关系进行深入研究。

（5）模型的推导过程还需要优化，对参数进行敏感性分析，忽略影响不大的参数，并尝试降低影响较大参数的确定难度。

（6）通过直接推导法或变换应力法，可将本文模型推广到三维形式来解决岩土工程中的边值问题，提高模型的实用性。