高中物理连接体模型透视

高峰

[摘要]连接体模型大致分为悬挂类、支架类、斜面类、板块类，文章采撷几则典例，对相关问题进行分析点评，以引导学生分类认识连接体模型，并在问题的分析、比较过程中适当归纳总结，以提升学生的解题能力。

[关键词]连接体;模型;高中物理

[中图分类号]G633.7

[文献标识码] A

[文章编号] 1674-6058（ 2020）35-0057-02

连接体是指两个或两个以上相互作用的物体组成的系统。在高考试卷中，经常出现连接体模型，甚至在压轴题中也会出现。连接体问题变化多端，考查内容多，能力要求高，很多学生在处理时感觉难度较大。因此，在实际教学时，教师要引导学生分类认识连接体模型，并归类分析各类连接体问题的解题思路，提升学生的解题能力。下面结合实例对典型的连接体问题进行分类例析。

一、悬挂类

悬挂类问题，一般牵涉绳，而绳对物体的作用力一定沿绳，要解决这类问题，可以灵活采用整体法和隔离法，并运用牛顿第二定律或平衡知识解决问题。

[例1]如图1，圆环A穿在一根水平放置的细杆上，用轻质细绳将小球B与圆环A连接起来。已知圆环A的质量是mA，小球B的质量是mB。因为存在水平向右的风，圆环A与小球B一起向

右匀速运动。此时，轻质细绳与竖直方向的夹角为θ，则（ ）。

A.风对小球B的作用力为F=mBgtanθ

B.突然风增大，小球B受到绳的作用力仍然不变

C.如果风力增加，水平杆对圆环A的力增大

D.杆和圆环A之间的动摩擦因数为mB/mA+mB

解析：如图2，分析小球B的受力可知：风的作用力为F=mBgtanθ，细绳对小球B的拉力为T=mBg/cosθ，因此A正确;假如风变大，根据T=mBg/cosθ，θ角变大，拉力也变大，因此B错误;将圆环A和小球B视为整体分析，整体重力为G总、水平杆对圆环A有向上的支持力Ⅳ、风力F水平向右、圆环A受到杆向左的摩擦力f。由平衡条件可得N=G总，f=F，因此杆对圆环A的支持力保持不变，可知C不正确;由N=G总=（mA+mB）g，f=F，F=

mBtanθmbgtan θ，f =μN得/μ=mA+mB，因此D错误。

点评：本题结合实际，考查悬挂类平衡问题。解决的办法是：运用整体法和隔离法，先用隔离法，并以挂件为入手点，分析挂件的受力情况，再以整体为研究对象，分析整体的受力情况。

二、支架类

支架类问题，一般牵涉轻杆。轻杆对物体的作用力一般沿杆.可以是拉力，也可以是支持力，解题时要具体分析。轻杆连接两球同轴转动时，两球具有相同的角速度，两球构成的系统机械能守恒（单个球机械能不守恒）。

[例2]如图3所示，在竖直平面内，将一个半径为R的环形槽固定住。已知环形槽内部光滑。将小球甲连接在一根轻杆上，已知轻杆的长度是√2R.球甲的质量是m。再在轻杆的另外一边固定一个小球乙，已知小球乙的质量是2m。将连接两个小球的轻杆放置在环形槽中。小球乙此时处于环形槽的最低端。将连接两个小球的轻杆由静止释放，则（ ）。

A.在下滑中，小球乙机械能的增加量等于小球甲机械能的减少量

B.在下滑中，小球乙重力势能的增加量等于小球甲重力势能的减少量

C.小球甲能够到达环形槽的最下端

D.从右向左返回时，小球乙能够回到环形槽最低端

解析：甲、乙物体组成的系统只有重力做功，机械能守恒。因此，下滑过程中甲球减少的机械能总是等于乙球增加的机械能，选项A正确;由于下滑过程中甲、乙物体的速度在变化，因此甲球减少的重力势能总是等于乙球增加的重力势能说法错误，选项B错误;若甲到凹槽的最低点时，乙到达与O点同一水平面的位置，显然机械能增加，选项C错误;杆从右向左滑回时，乙回到凹槽的最低点时机械能不变，选项D正确，答案选AD。

点评：解决支架类问题，常用系统机械能守恒、功能原理及牛顿第二定律等知识解决问题。

三、斜面类

斜面类问题，历来是高考命题的热点，可以考查斜面上物体的平衡，也可考查斜面整体的平衡，还可以考查加速问题。解题时应注意整体法和隔离法。

[例3]如图4，将一个斜面体放在水平面上。已知水平面粗糙，斜面体质量是M，倾角是θ。将一个物体放在斜面体上，用力F沿着斜面向下拉动物块。已知物体做匀速直线运动，斜面体保持静止，则下面选项正确的是（ ）。

A.斜面体有相对地面向右的运动趋势

B.斜面体受到地面的摩擦力为Fcosθ

C.斜面体受到地面的支持力是（M+m）g

D.物块受到斜面体的摩擦力为F

解析：可以用整体法分析，将斜面体与物块当成整体，整体的重力为G（大小等于mg+ Mg），地面对斜面的支持力为Ⅳ，对物块的拉力为F，斜面对地面的摩擦力为^，整体平衡，可以得到：f地 向右，大小是f地=Fcosθ，N=（M+m）g+ Fsinθ，因而B正确，A和C都是错误的。如图5，再将物体隔离开来，F+ mgsinθ=f，因此D错误。

点评：（1）几个物体都静止;（2）几个物体都匀速运动;（3）整体内一部分静止，其他匀速运动。这三种情况可以尝试使用整体法。

四、板块类

板块类问题是一类重要的连接体模型，牵涉两个物体的相对运动，解题时，要根据两物体的受力特点、运动特点，判断两物体是否发生相对运动，然后，运用整体法和隔离法解决问题。

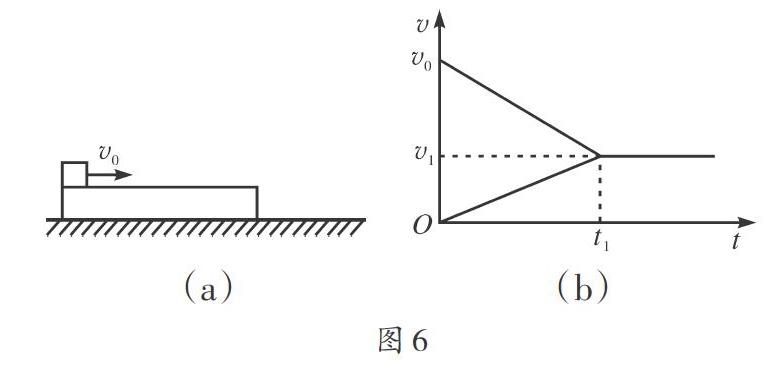
[例4]如图6（a）所示，在水平桌面上放一块长木板，已知桌面和长木板間没有摩擦力。从0时刻开始，一个小物块获得了一个速度v0，冲上了长木板。图6（b）所示为长木板和小物块的速度一时间图像，其中t1、v0、v1都是已知的。重力加速度为g。根据这些信息能求得（ ）。

A.长木板的长度

B.小物块质量与长木板质量的比值

C.长木板与小物块间的动摩擦因数

D.t1时刻长木板的动能

解析：由v-t图像的面积表示位移，可以求得从t=0开始到t1时刻物块比木板多发生的位移，但不能求得木板的长度;由v-t图可得木板和物块的加速度大小的比，物块和木板所受合外力都为物块和木板间的滑动摩擦力，因此物块和木板的质量比等于二者加速度的反比，选项B正确;物块的加速度大小为a=v0-v1/t1，对物块应用牛顿第二定律μmg=ma可得物 块与木板之间的动摩擦因数，选项C正确;由于不能求得木板的质量，因此不能求得木板获得的动能，选项D错误。

点评：物块和木板都在恒力作用下做匀变速直线运动，v-t图像的面积表示位移，v-t图像的斜率表示加速度，本题可利用比值法和图像法解决。

解决连接体问题，要利用整体法和隔离法进行分析。具体解题时，首先要搞清物体间的连接关系，然后分析清楚物体的运动情况，如果属于平衡类问题，一般从力的观点选择研究对象后求解;如果不属于平衡类问题，一般利用牛顿第二定律，确定物体间的运动关系后解方程求解;对于曲线运动和部分不牵涉加速度和时间的直线运动问题，常用能的观点解决问题。

（责任编辑 易志毅）