系统配分函数与子系配分函数关系探讨

王赵武， 雷建飞， 李立本

(河南科技大学物理工程学院， 河南洛阳 471023)

0 引言

配分函数方法是统计物理学的标准方法， 它的计算是统计物理计算中的核心内容[1-3]. 统计物理学教材中一般把配分函数分为系统配分函数ZN和子系配分函数Z1两种， 对于由全同粒子构成的近独立系， 这两种配分函数之间的关系如下.

那么对于全同粒子构成的近独立系， 粒子是否可分辨是唯一区分这两个公式的适用条件吗？ 是否还有其他条件？ 如果有， 是什么条件？

1 分析

为了分析这个问题， 我们先看一道题[4]：

由两个全同粒子组成的体系， 每个粒子有三个量子态， 能量为0，ε， 2ε. 体系同温度为T的大热源接触. 就下列情况写出体系的配分函数Z.

(1)服从经典统计， 粒子可分辨;(2)服从经典统计， 粒子不可分辨.

对于问题(1)， 如果全同粒子定域， 则可分辨， 经典统计中， 每个量子态上占据的粒子数不受限制， 系统的配分函数为

其中s表示系统的所有微观状态.

此系统的所有微观状态如下所示.

由于该系统为近独立系， 可以利用系统配分函数和子系配分函数的关系得到这个结果.

两者结果一致.

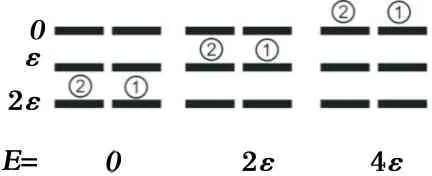
对于问题(2)， 如果全同粒子非定域， 则不可分辨， 系统所有的微观状态为

所以

两者结果不一致.

一般热力学统计物理教材中对于理想气体的系统配分函数和子系配分函数的关系使用的是

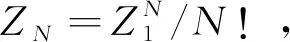
2 结论

对于近独立系， 统计物理中先求子系配分函数， 然后利用子系配分函数和系统配分函数关系求系统配分函数， 并进一步求系统性质时是有条件的， 即体系需要满足经典极限条件. 而当体系不满足经典极限条件时， 只能利用定义式求系统的配分函数.