短波电离层的吸收损耗计算

雷前召， 张修兴， 何 冰

（渭南师范学院物理与电气工程学院，陕西渭南 714099）

短波（频段3～30 MHz）的远距离传输主要经由电离层反射进行，故短波又称天波或电离层波. 地球大气的上层气体分子因受太阳辐射的紫外线、X射线、太阳喷射的粒子以及宇宙射线作用［1］，发生电离而形成电离层［2］. 按距离地面高度不同，通常将电离层分为D、E、F层，但距离地面最近的D层电离程度较小，对电波传播影响也小. E层距离地面90～140 km，F1层200～300 km，F2层300～400 km，F2层的电离密度最大，对电波的反射作用也最强.

短波在无线电广播和通讯［3］、在国防、科技领域以及实际生活中均发挥重要作用，但短波频段狭窄拥堵，通信频点的选择有限，更要考虑电离层D、E、F层的变化的影响［4］. 短波在选用通信频点时，应尽量接近电波能返回的最高可用频率（MUP），根据实际经验，通常选取最高可用频率的80%～90%作为工作频率. 一方面能避免当电离层变化较大、电离层电离分子浓度起伏加大［5］，增加了电波穿透电离层的风险；另一方面，选择频率偏高的短波，电波在电离层的传输与反射距离都会加大，电离层吸收损耗也会加大.

短波传播中的损耗包括4部分：电离层吸收损耗［6］，自由空间传播损耗，多跳地面反射损耗和额外系统损耗［7-8］. 电离层传播损耗模型很多［9-10］，本文讨论的短波电离层损耗是基础.

1 短波通信的电离层吸收损耗模型

短波可用较小的发射功率直接进行远距离通信，短波通信主要通过天波和地波两种传输途径来实现信号的远距离传输［11-12］. 由于地波最大传播距离30 km，天波一跳距离超过100 km，因此30至100 km区间是短波通信的“盲区”［13］. 电离层平均高度约为273 km［14］，短波传播距离是经电离层反射的距离，不是发射机和接收机之间间距.

电离层对短波能量的吸收有如下特性：天波经F2层传播及反射时，被吸收的电波能量一般不超过1 dB，但经E层传播及反射时，E层对其吸收能量很可观. D层白天吸收短波能量甚微，夜间D层消失. 因此，计算短波在电离层的传播损耗主要是计算E层对电波能量的吸收.

用图1示意说明短波的电离层损耗计算方法，P为发射台所在位置，Q为接受台所在位置，P′和Q′分别为电波上、下行透过电离层E层的穿过点，A和A′分别为电波在F2层和E层的反射点.

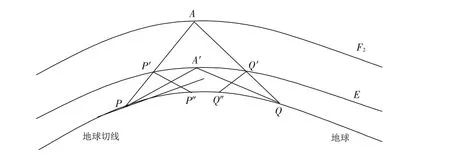
图1 天波反射路径示意图Fig.1 Sky-wave reflection path diagram

短波经电离层的一跳接收信号，电离层E层的吸收损耗建立有以下数学模型［15］：

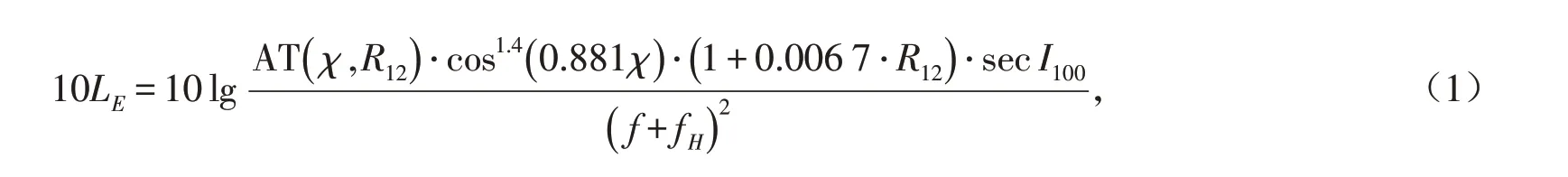
其中：AT( χ,R12)为吸收因子，其数值由天顶角χ 和太阳黑子数R12决定；I100为来自P点电磁波在A′处的入射角；电台工作频率f 和磁旋频率fH的单位均取MHz. 公式（1）的最终计算结果涉及短波电离层传输一众相关概念及其计算，通过实例示范如下.

2 短波电路几何参数及E层损耗计算

某短波电台，发射台和接收台分别设在100.0°E，35.0°N，115.0°E，32.5°N，电台频率为15 MHz，计算某年六月某日干扰电台工作在12时的电离层损耗.

发射台和接收台所在位置用P、Q两点表示. 由于电离层的不稳定性，每年每月每天每时都在变化，电离层的传播损耗计算都是临时的，也就是说某时的损耗计算只能适用于该时，而不能适用它时. 电离层短波损耗主要考虑E 层损耗，但由于电离层变化受到太阳黑子、地理纬度以及地球磁场和时间等诸多因素的影响，在利用（1）式求解短波天波损耗时，先后会涉及这些量的计算：PQ 大圆距离，电离层高度，电波射线仰角Δ 及到达电离层的入射角β，太阳黑子数，P′、Q′和A′在地球表面投影的经纬度及吸收因子，电波在P′、Q′和A′处的入射角，电离层E层吸收因子，P′、Q′和A′的天顶角.

2.1 大圆距离

假设地球是球形，设地表任意两点与地心所在平面与地球表面相交，交线为大圆周长，不在地球直径两端的两点分圆周为一长一短两部分，较短部分就是两点的大圆距离. 如图2所示，P为发射电台所在地球表面位置，Q为接收电台所在地理位置. 大圆弧线所对的地心角φ 由球面三角的余弦定理计算［16］

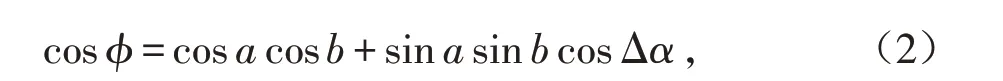
式中：a（=90°-βQ）、b（=90°-βP）、Ф为球面三角PQN的三个大圆弧NQ（a）、NP（b）、PQ（c）各自对应的地心角，βP和βQ为P点和Q点所在处的纬度；Δα 为Q 与P两点的经度的差值.

将P 和Q 点的经纬度值代入公式（2），得到Ф=12.707°，则大圆距离c

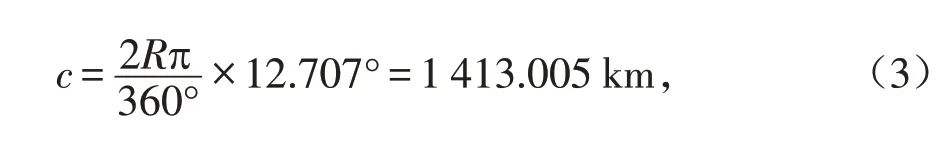
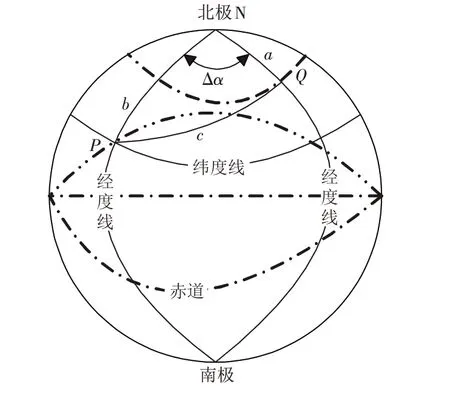
图2 大圆距离Fig.2 Great circle distance

其中：地球半径R取值6 371.230 km.

2.2 电离层反射点高度

F2高度值随月份不同而变化，可通过查表1［15］得到所需电离层高度，电离层F2上反射点A的纬度介于P、Q之间，故其纬度大于35°，因此电离层高度应选363 km、而不是300 km. E层高度不随月份变化，工程计算一般取为100 km.

表1 电离层（F2层）高度与季节、时间的关系Tab.1 The relationship among the heights of the ionosphere（F2 layer），seasons and times

2.3 地面仰角及电波进入电离层入射角

如图3 所示，地平线PF 是地球切线，PQ 直线中点D 到地球表面的最短距离（即DE）为地球曲率高度.PD=R sin α=705.055 4 km（α=6.353 5°），OD=R cos α=6 332.098 3 km，ED=R-DO=39.131 7 km.

CE为F2层电离层高度（363 km），则F2层曲率高度CD=ED+EC=402.131 7 km. 设E层反射点为CE，其曲率高度CED=139.131 7 km.

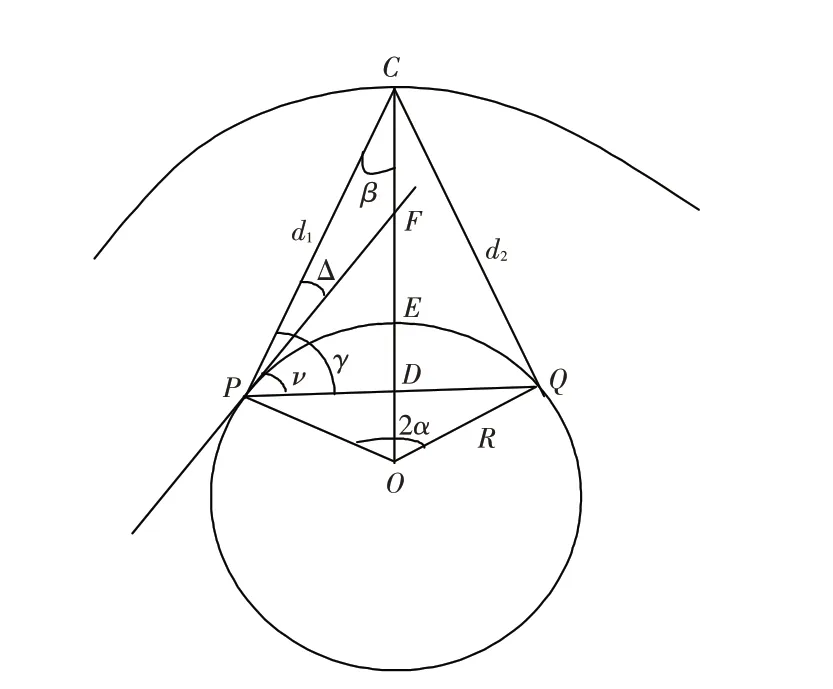
图3 地面仰角Δ、电波到达电离层的入射角βFig.3 The ground elevation angle Δ，and the incident angle β of the radio wave reaching the ionosphere

具体结果：γF2=29.698 5°. 同理可得PQ射线相对E 层反射点（CE）的射线仰角γE=arcsin（CED/PCE）=11.163 0°.

电波的地面仰角为［16］：

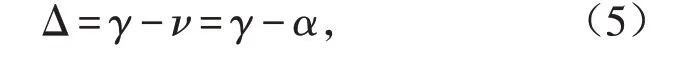
式中：Δ 为电波到达电离层的射线PC相对地球切线PF 所张的角度；弦切角ν 等于弦PQ 所对圆心角（即大圆距离PQ所对地心角）的一半（α）. 故有α=c/2=6.353 5°，则由（5）式可得F2层、E层地面仰角值分别为ΔF2=23.345°，ΔE=4.81°.

2.4 太阳黑子数

黑子数多则太阳离子辐射能力强，电离层对短波信号的反射就强，所以在太阳黑子的高峰期，能听到更多平时不易听到的小功率电台. 太阳黑子数每11年有一规律性小变化、60年一规律性大变化，数目在0到200范围内. 本例未设定具体年份，不失一般性，选取太阳黑子数中值R12=100.

2.5 P′、A′、Q′各点在地球表面投影的经纬度，各点在E层的吸收因子

电波在F2层反射，上下行穿过E层，其穿过点为P′和Q′. 根据E和F2层反射点的射线仰角，在图4中查询E层的截止距离，即仰角曲线与E层高度交会点在底横线上标出的大圆距离. 其距离中点就是P′投影点到P点的距离以及Q′投影点到Q点的距离.

由电波F2层反射点的地面仰角ΔF2=23.345°、E 层高度100 km，在图4 中［18］查得电波在E 层截止距离dE=440 km，因此PP′=QQ′=440/2=220.0 km. A′在P、Q中点，设A′在地表投影为A″，则PA″=QA″=1 413.005/2=706.503 km.

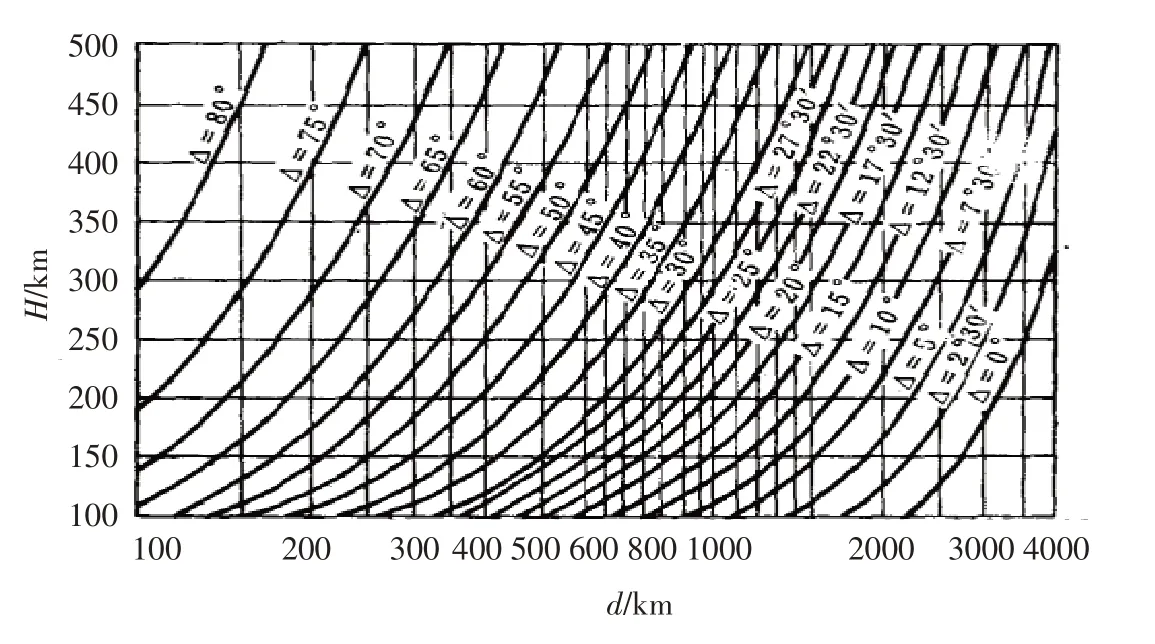
图4 电离层反射高度、通信截止距离和射线仰角之间的关系Fig.4 The relationship among ionospheric reflection heights,communication cut-off distances and ray elevation angles

根据P，Q的经纬度，用透明纸罩在图5［16］上划出PQ直线. 把划好的直线放到图6上，因P、Q间的大圆距离已知（1 413.005 km），确定所画直线PQ在图6［16］大圆中对应的比例尺，再根据PP′、QQ′的数值，标出P′、Q′在直线PQ上的位置；A′投影点A″在PQ直线中点，标出A″点. 然后将透明纸移到图5上，查P′、Q′以及A′投影点的经纬度. 由于使用相同的比例尺，这里使用直线视线距离代替大圆有效距离是可以接受的.

测量结果，P′、Q′在地表投影的经纬度分别为（103.0°E，36.0°N）、（113.0°E，37.5°N），A″经纬度（108.0°E，37.0°N）.

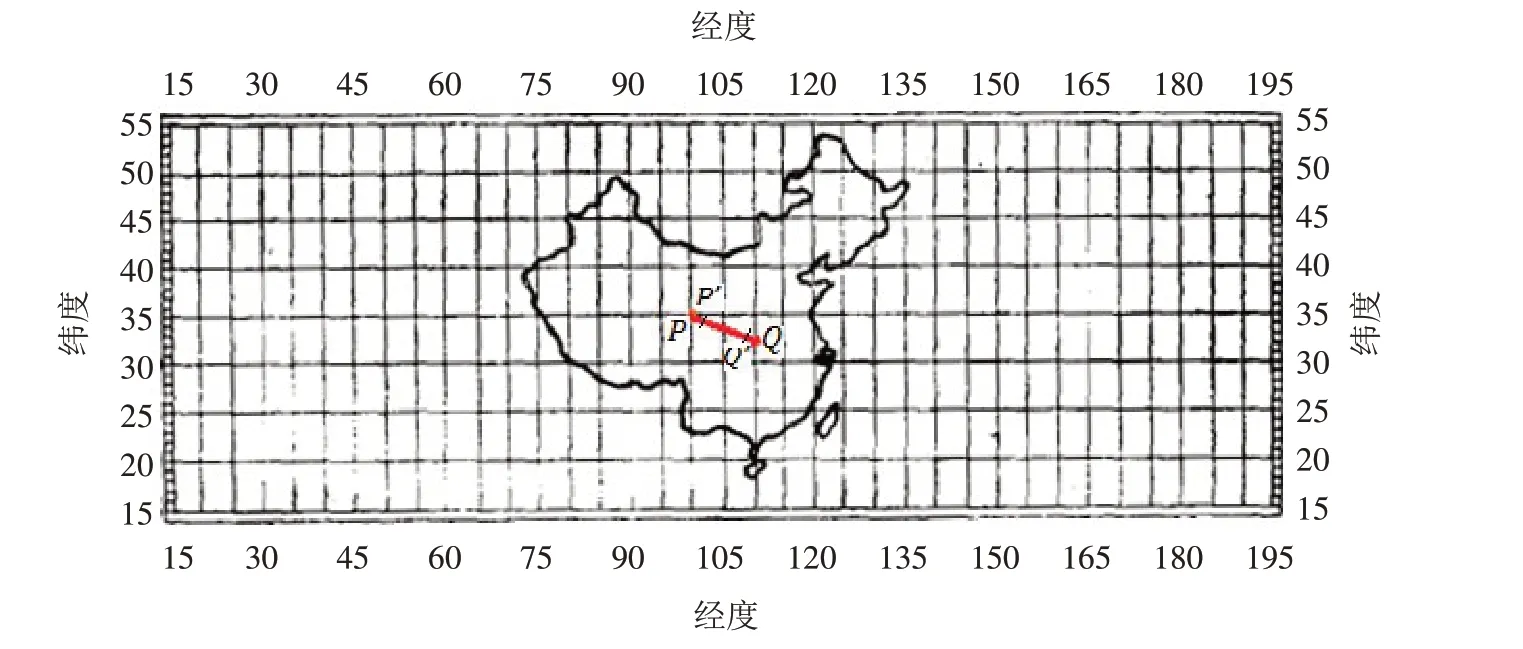
图5 地图Fig.5 Map

图6 大圆图（单位为103 km）Fig.6 Great circle chart（Unit：103 km）

地球表面任一点的地磁场总强度的矢量方向与水平面的夹角称为磁倾角，改进型磁倾角 ||X［17］增加了地理纬度的因素. 利用P′、Q′、A′在地表投影的纬度，由图7［15］查得各点改进型磁倾角 ||X 、磁旋频率fH值为：（ ||X =45°，fH=1.325 MHz）P′；（ ||X =47°，fH=1.35 MHz）Q′；（ ||X =46°，fH=1.35 MHz）A′.

根据图8［16］磁倾角 ||X 和吸收因子AT（0，0）关系查得各点吸收因子数值：AT（χ，R12）P′=320，AT（χ，R12）Q′=320，AT（χ，R12）A′=320.

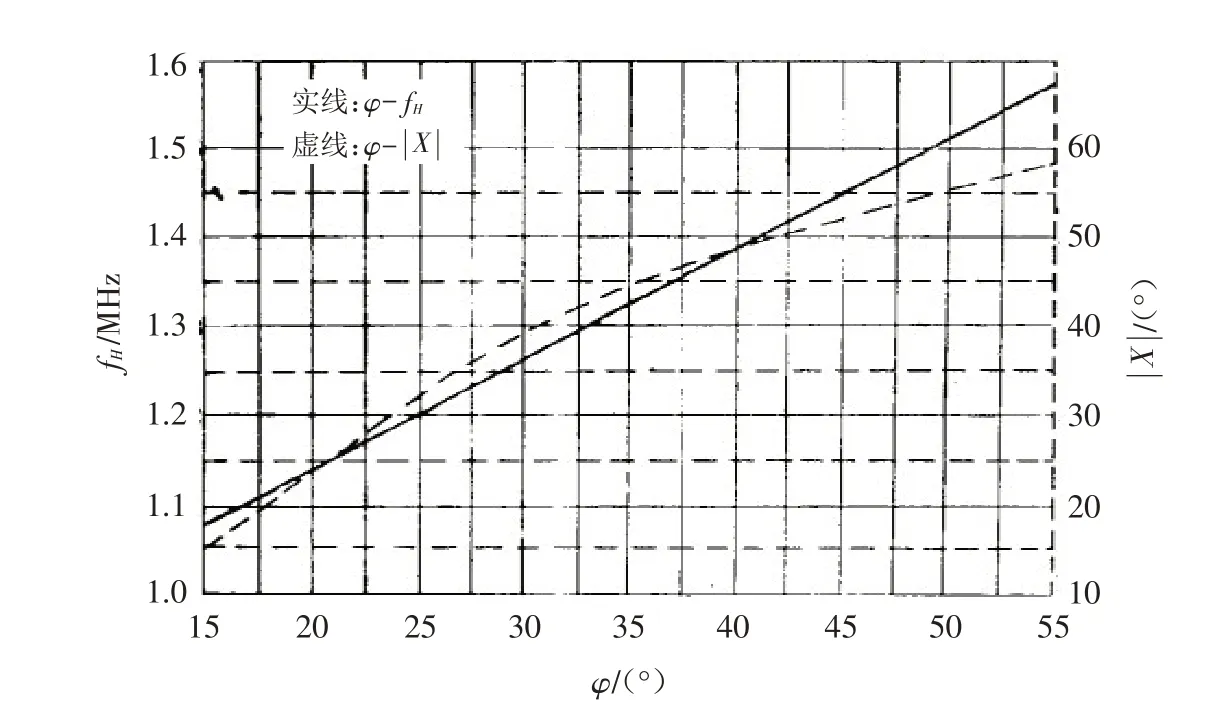
图7 地球纬度φ 和磁旋频率fH 与磁倾角 ||X 的关系Fig.7 The relationship among the earth’s latitude φ，the magnetic rotation frequency and the magnetic inclination ||X

图8 磁倾角 ||X 和吸收因子AT（0，0）的关系Fig.8 The relationship between the magnetic inclination ||X and the absorption factor AT（0，0）

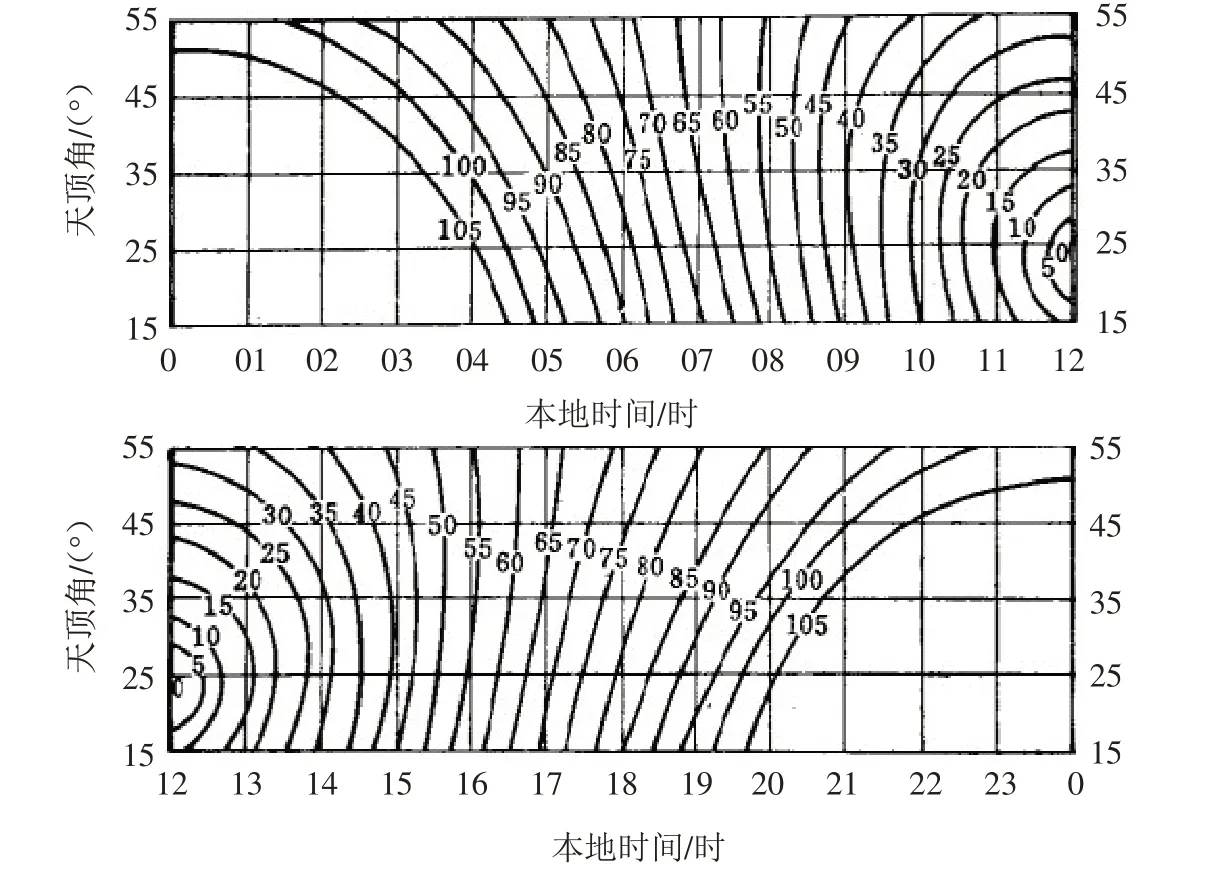
图9 六月份天顶角Fig.9 Zenith angle in June

2.6 天顶角

垂直入射地球表面的太阳光线、再继续延伸到地心的直线，与电台所在点到地心的直线之间的夹角称为电台所在处的太阳天顶角［18］，天顶角会影响遥感反射率［19］.

太阳某处的天顶角由其纬度和时间决定. 地球表面经度平分360°，每经度时差为4分钟. P′、Q′、A′和Q点的经纬度已知，由P点时间和经度，可推算出P′、Q′、A′和Q的时间.

计算时间是以太阳直射到东经120°，12时零分零秒为参考标准时间（即北京时间），计算东经120°以西某位置的时间，需减去经度差对应的时间（以东则改为加）.

由此计算P′点时间（120°-103°）×4=68 min，12 时延迟68 min 即10 点52 分；类似地得到Q′点时间延迟28 min即11点32分，A′点时间延迟48 min即11点12分. 根据它们的时间和纬度，在图9中［15］查得它们各自的太阳天顶角：χP′=20°，χQ′=16°，χA′=18°.

2.7 电波在电离层反射点P′、Q′、A′处的入射角

计算入射角I100，直接利用公式I100=arcsin（0.985 cos Δ）（Δ为来自发射电台（P点）的电波相对于F2或E反射点的地面倾角）［16］，电波经F2层反射时，上、下行穿过E层对应的入射角为I100P′=I100Q′=arcsin（0.985 cos ΔF2）=64.738°，电波经E层反射的入射角I100A′=arcsin（0.985 cos ΔE）=78.971°.

电离层吸收损耗包括经F2层反射的E层吸收损耗（LP′，LQ′）和经E层反射的E层吸收损耗LA′，将以上计算的相关量带入公式（1），分别得到

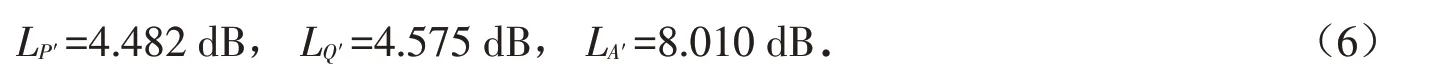
经E层反射的E层吸收损耗：

经F2层反射的电波在P′和Q′点只是进行了反射的一半，其E层总吸收损耗：

所以天波一跳的电离层E层总吸收损耗为

此结果只适合此时、此处，虽不至影响接收点正常工作所需的信噪比［20］，但已是不容小觑.

3 结语

电离层的损耗吸收计算也是短波的天波干扰计算的依据，将上文实例中的接收电台视为工作电台，则实例中的发射电台就是干扰源，其干扰源传输能量减去上述电离层吸收损耗量才构成对工作电台的干扰因素.另外，上述电离层损耗计算只是短波一跳的电离层吸收损耗，超过一跳还需要计算电离层反射落地的地面吸收损耗. 由于电离层的不稳定性，影响电离层吸收损耗的参数众多，电离层多径效应、电波极化方式、聚焦效应以及天线不稳定引起的增益下降都能引起电波能量损耗，这些损耗计算非常复杂，当前我们对其计算尚有很多局限性，需要我们对电离层进行更多的实时监测. 中国电波传播研究所（中国电子科技集团22研究所）不久前在西安电子科技大学建立电离层观测站，笔者有幸参与观测站的测量与科研. 电离层观测站的建立无疑会给我们提供更多本地电离层有价值的参数，同时也必将进一步促进短波电离层传播及应用研究.