基于气象系统指数的辽宁地区中长期降水预测回归模型的建立及应用
孙海波
(营口市水利事务中心,辽宁 营口 11500)
0 引 言
辽宁省降水主要集中在夏季,初夏和盛夏是辽宁地区暴雨集中的两个节气[1]。辽宁地区初夏和盛夏降水量占全年降水量总量的比重分别达到25%和45%,每年汛情形式研判都需要对夏季降水量进行中长期预测,一般主要预测7-8月份的降水量[2]。对于降水量的中长期预测近些年来,取得不少研究成果。这其中大体可以归类为两种方法,第一种方法主要采用数理统计方法,通过建立回归方程,对中长期降水进行预测,这种方法的优点在于具有强大的数理统计功能,通过建立经验回归模型,对降水变量进行中长期预测,缺点在于需要较长系列的降雨数据系列,且模型验证难度较大[3-6]。第二种方法即采从气象变化特征分析,通过建立气象指数与降水的相关方程,实现降水的中长期预测,这种方式的优点在于物理基础强,充分考虑降水因子和气象因子之间的相关度,这种方式的缺点在于由于气象系统影响较为复杂,需要建立多种气象系统指数和降水之间的回归方程,从而满足降水中长期预测的精度需求[7-11]。邹铠杰研究表明当前气象系统指数已可满足降水中长期预测的需求[12]。为此文章从气象变化特征出发,基于大气环流因子、海温外强迫因子等气象系统指数建立辽宁地区初夏和盛夏降水量的多因子中长期预测模型,对辽宁地区夏季降水中长期进行预测,
从而为防汛抗旱决策提供支撑依据。
1 回归模型构建步骤
对方程中的因子变量进行引进和剔除步骤的逐步回归过程,称为双重筛选逐步回归。具体技术通常使用标准化回归方程,其技术过程如下。
1)第一步,建立初始矩阵。
建立标准化变量的多元回归方程正规方程组,在p个因子相关阵基础上面扩展一列,该列为p个变量与预报量的相关系数项链,并组成一个新的增广的对称阵,记为:
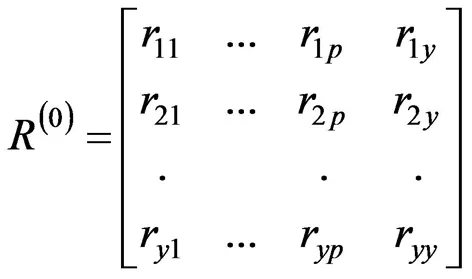
(1)
矩阵R右上角的“(0)”表示第0步,其矩阵中元素也类似表示。对矩阵某列进行逐步消去求逆运算,其矩阵右端列对应元素就是解,即对应变量的回归系数。按消去求逆的性质有:
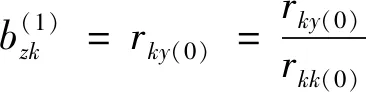
(2)
2)第二步,引入引自变量。计算各因子变量方差贡献:
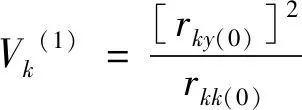
(3)
对第k个因子做统计检验时可用统计量:
(4)
采用F检验对统计变量进行分析,对其中检验值最大的变量进行实际检验,其中对Vmax(1)=Vk(1)进行假定,若通过检验,则将变量进行选取,此时对于R(0)值进行消除,修正为R(1),此时计算的rky(1)表示为基于选取变量构建的回归系数标准值。
3)第三步,继续因子变量的引入。
对各变量的方差贡献率进行回归系数标准值的计算,通过对矩阵R(0)中的变量进行消除,这样可以简化计算流程。在实际计算中需要对各计算步骤的变量进行选取,并重点分析其变量的方差贡献率,均可采用类似方法进行分析。通过前面各步骤进行多个变量选取后,考虑到下一个未选取的变量方差贡献度时,对第k个变量方差贡献率进行计算:
(5)
对其他未选取的p-1个变量进行方差贡献率的计算,结合前面方差贡献率的计算结果,采用R(0)进行多次消去求逆分析,得到R(l)矩阵对应的变量,其中如果第k个变量的方差贡献率最大,则基于Vmax=Vk(l+1)进行变量的检验,检验统计量计算方程为:
(6)
则可得计算Q(l+1)的公式为:
Q(l+1)=Q(l)-Vk(l+1)
(7)
其中:
Q(l)=ryyl
(8)
使用下面的统计量进行检验,即:
(9)
符合自由度分别为1及n-(l+1)-1的的F分布。未进行选取的变量按照公式(5)进行方差贡献度的计算,选取方差贡献度最大的因子进行检验,当检验通过后,则将变量进行选取,对各变量对应的序列值进行消减,并基于该变量构建标准回归方程。
4)第四步,剔除因子。
当变量选取后,各变量方差贡献会产生相应的变化,对于不能通过检验的变量进行剔除,采用统计检验的方式对未通过检验的变量进行剔除,当全部因子经过检验和剔除后,对无因子变量进行筛选,若未通过检验,则进行剔除,再进行其他变量因子的选取,重复以上步骤,直到所选变量因子均通过检验为止。
5)第五步,计算结果。
当引入l个变量对回归方程进行构建后,对未通过检验的变量进行剔除后,进行R(0)到R(l)的转换,构建的回归方程主要形式为:
(10)
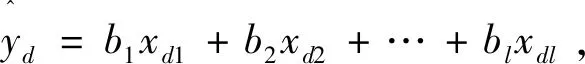
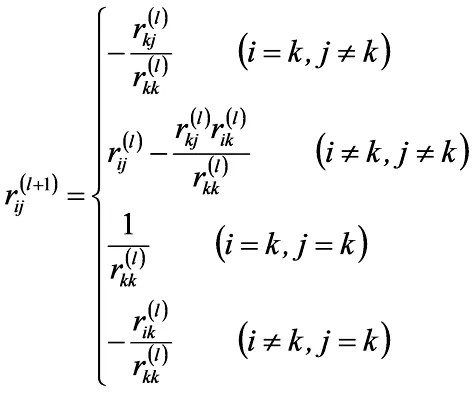
(11)
在每消去一列时,就得到对应该列因子回归方程的解,以及系数矩阵的逆矩阵。求解过程与消去列的顺序无关。对已经消去的列进行再消去等于恢复该列未消去前的元素。
2 模型应用
2.1 数据概况
文章将利用1951年1月至今的逐月130项环流指数,建立起辽宁省夏季分区域分时段的降水量预测模型。结合建立的回归方程对前一年1月至当年1月的预测变量进行当年夏季的降水量进行预测,则预测因子年限为1965-2014年,拟合年限为1966-2015年。
2.2 初夏降水预测模型
结合回归方程构建原理,结合辽宁地区初夏1951年1月至今的逐月130项环流指数,对各分区的降水中长期预测回归模型进行建立,结果见表1。

表1 初夏降水回归模型建立结果
从表中可以看出,对初夏降水有影响的环流指数主要包括极涡面积指数、极涡中心经向位置指数、各地的副高北界位置指数、副高面积指数等。文章结合各分区实测降水值和各模型的拟合值进行对比,发现所建立的模型与实测的情况拟合效果非常好,其中全省降水量模型对实际降水量的模拟效果最好,两者相关系数高达0.90,在模型中不仅可以模拟出降水平常值,还可模拟出降水的极值情况,这在其他模型中是非常少见的,回归方程的可靠性非常高[13-15]。
2.3 盛夏降水预测模型
在初夏回归模型构建的基础上,结合盛夏时期逐月130项环流指数,对各分区的盛夏时期降水中长期预测回归模型进行建立,结果见表2。

表2 盛夏降水回归模型建立结果
从表中可以看出,对盛夏降水有影响的环流指数主要包括极涡面积指数、极涡中心经向位置指数、各地的副高北界、脊线位置、面积指数以及一些海温指数等。前期因子的时间主要集中在前一年冬季(前一年11月至当年1月)。通过对各分区拟合值与实测值的对比可以发现盛夏的模型与实测的情况拟合效果也非常好,其中,除东南部外,其余地区的拟合值与实测值的相关系数均在0.8以上。并且对序列当中降水的极值情况也可进行模拟,因此构建的回归方程的可靠性非常高。
2.4 模型验证结果分析
在初夏和盛夏回归模型构建的基础上,结合2017年初夏和盛夏的实测降水量对辽宁省不同区域中长期降水预测值进行验证,验证结果见表3。
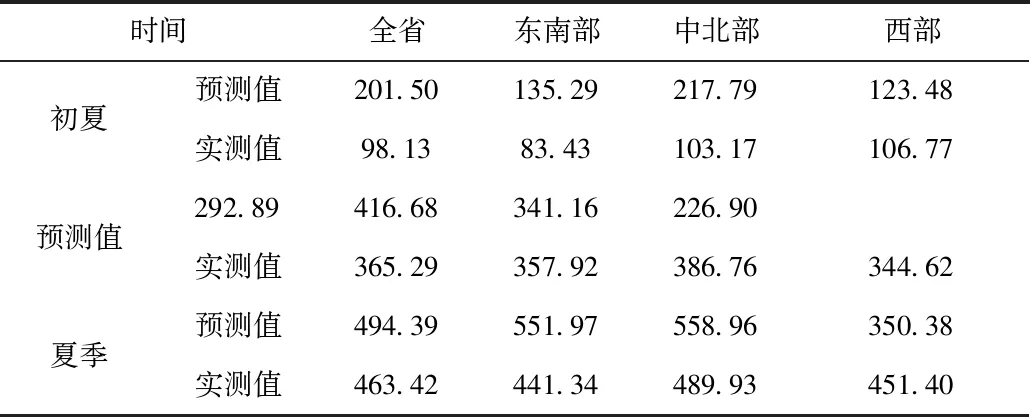
表3 2017年降水量预测与实测对比表
从模型初夏和盛夏两个季节不同分区的降水中长期预测值和实测值对比结果可看出,盛夏的预测值和实测值的相关度要好于初夏预测相关度,这主要是因为初夏气象环流指数对于辽宁地区降水影响程度要小于盛夏时节,但在初夏各区域降水预测值和实测值的相关系数总体也可达到0.70。而进入盛夏时节,大气环流因子及其他气象系统指数对辽宁地区盛夏降水影响的主因,使得其基于气象系统指数建立的回归模型相关度较好,因此回归模型预测降水值和实测降水值吻合度较高。将初夏降水与盛夏降水的拟合值相加,得到夏季降水量的拟合值,从分析结果可看出,在辽宁各分区,建立的回归方程的相关系数均可达到0.80以上,此外,各分区回归方程对降水极值年模拟也较好。构建的基于气象系统指数的降水中长期预测回归模型的可靠性较高[13-15]。
3 结 语
根据上述分析可以看出,对初夏降水有影响的环流指数主要包括极涡面积指数、极涡中心经向位置指数、各地的副高北界位置指数、副高面积指数等,所建立的模型与实测的情况拟合效果非常好,其中全省降水量模型对实际降水量的模拟效果最好,两者相关系数可达0.70。对盛夏降水有影响的环流指数主要包括极涡面积指数、极涡中心经向位置指数、各地的副高北界、脊线位置、面积指数以及一些海温指数等,前期因子的时间主要集中在前一年冬季(前一年11月至当年1月)。盛夏的模型预测结果与实测的情况拟合效果非常好。将初夏降水与盛夏降水的拟合值相加,得到夏季降水量的拟合值,不管全省还是各分区,本研究对降水量的模拟效果非常好,除东南部以外,其余地区拟合值与实测值的相关系数均在0.8以上,并且对降水极值年模拟也较好。因此构建的模型的可靠性较高。

