多时间尺度下Kriging与IDW空间插值方法的适用性研究

肇毓锋，吴 奇

(1.辽宁省水利事务服务中心，沈阳 110003；2.沈阳农业大学，沈阳 110866)

0 前 言

在人类社会的发展中，降雨是至关重要的，尤其体现在生态环境的整治、地区水文、水资源的分配和利用、旱涝灾害分析。当降雨过少或达不到农作物灌溉的标准时，常常会发生干旱减产现象。一般来说，人们都是通过自动雨量观测站或者分散的气象台站来获得一个地区的降雨数据，然而可供测量的水文站点也不多，且可供测量站点的空间布局也有不合理的，如若想要获得多年的气象资料更是困难重重。使用地区部分站点的实测降水数据进行空间插值是当下获得降雨资料的卓有成效的办法[1]。

空间插值是能表现该区域地理特性的空间分布特征的样本，通过运用已知的地理要素来分析未知的空间特征，也就是利用已知空间数据预测未知领域，从而得出预测的数据值；他的本质就是采用部分已知点对陌生研究地区进行空间预估[2]。空间插值可以采用的方法比较多，常用的有反距离加权法(Inverse Distance Weight tension IDW)、张力样条函数法(Spline With Tension)、趋势面法(Trend)、普通克里金法(Ordinary Kriging)、协同克里金法(Ordinary Cokriging)、全局多项式插值(Global Polynomial Interpolation)、局部多项式插值 (Local Polynomial Interpolation)等[3]。实验得出的结论基本都是：对于空间数据插值方法，不存在适合于所有条件的空间插值；然而如若空间变量不同，地域不同和时空尺度不同，那关于最优内插法的结论也是不准确的[4]。而事实上不可避免的是使用相同数据和不同方法得到的结果也可能存在差别。研究地区的地形地貌和数据不同，同时降雨时空分布不均匀、趋势性、周期性等特征都会造成结果存在差异。因而，就降雨量来说，科研人员尝试采用不同方法研究降水序列，并运用ArcMap对地区所有离散数据进行空间插值，以期取得研究区域降水量的空间分布。

由于人们不断对降雨的精度提出更高的要求，因而通过细致分析和比较多种空间插值方法，选择出最适合某一地区的就显得尤其重要。文章选取吉林西部平原区为研究区域，对比IDW插值法和Kriging插值法并用典型的误差分析来估测两者插值精度，总结两者差距的原因，为今后的降水空间插值研究能有所帮助。

1 数据处理方法

1.1 研究区概况

吉林西部平原内部有东、西两片闭流区，面积约12959 km2，为平原区面积的24%。西部闭流区主要为风沙地貌，洼地和沙垅交错分布。东部闭流区的主要地貌同样为风沙沉积地貌，其内部由于地下水以及地表水排泄缓慢，有大量的天然湖泊分布，如查干湖等。近年来，由于全球气候变化和人类活动加剧的共同影响，吉林西部平原区的环境因素也出现了明显变化，其后果主要体现为土地荒漠化加速、水体面积减小，进一步使得土壤盐碱化、土地沙化、水土流失和水质受到污染。吉林西部平原研究区概况，见图1。由图1(a，b)可以看出，吉林西部平原区高程约在108-583m，总体呈东南高、西北低的态势，且东南部高程变化明显。

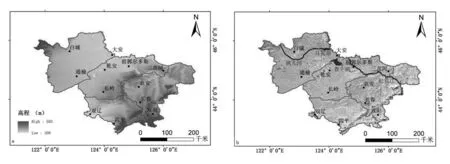
(a)研究区高程图 (b)研究区地形图

1.2 数据处理方法

文章用到的降雨量数据来源于吉林西部平原区共12个测量站点，站点名称及位置信息，见表1。利用这12个站点1975-2015年的实测降雨资料对吉林西部平原区年际降雨和生长季降雨进行时间演变分析。并将白城、双阳预留作为检查站点，根据剩余10个站点数据进行基于IDW和Kriging法的空间特征分析，最后使用白城、双阳站点的实测值与空间插值结果比较，以进行空间插值的误差分析。

表1 站名及位置

1.3 分析方法

IDW插值(反距离权重法)，是空间插值方法中的一种[5-7]，在1972年被美国国家气象局首次提出。其逻辑支撑是地理学第一定律——相近相似原理，即认为插值点受已知样本的影响受到插值点与已知点的距离控制，距离越近则影响越大，距离越远则影响越小。IDW插值的计算公式可表示为：

(1)

式中：Z(X0)为待估计的X0点属性值；Z(Xi)为X0点周围局部区域内第i点Zi的属性值；n为局部邻域内点的个数；Wi为Xi点对于X0点的权值。反距离的幂值依赖于反距离权重法。

Kriging插值法(克里金插值)，也称空间局部插值算法。这是在变异函数理论和结构分析的基础上，在一定区域内对变量计算无偏最优值的方法，在逐步改进中已成为地理统计的主要方法之一[8-9]，并衍生出不同的克里金插值方法。

克里金插值的计算公式可表示为：

(2)

式中：Z(X0)为X0处降雨量估计值；Z(Xi)为Xi处的观测值；λ为Kriging(克里金)权重系数；λi为Xi处的Kriging权重系数；n为观测点个数。

目前，一般使用交叉验证法来验证空间插值的误差，计算样本实测值与估算值两者间的误差，借此来估算两种插值方法的精度。通过计算平均绝对误差(MAE)和均方根误差(RMSE)来求出IDW插值(反距离权重法)和Kriging插值(克里金插值法)的空间插值精度。其中，平均绝对误差(MAE)可以有效评估计算值与真实值可能的误差范围，而均方根误差(RMSE)则可以反映利用样点的估算灵敏度和极值效应。并且，如若MAE和RMSE这两个数值越大，代表插值方法的精度越差，相反代表越好。

MAE和RMSE的计算公式分别如公式(3)和公式(4)所示：

(3)

(4)

式中：Qi表示第i站的实测降雨量；Ei表示第i站的预测降雨量；n表示用于检验的站点数。

2 结果与分析

2.1 吉林西部平原区降雨时间演变特征

棕色折线图为41a间的降雨量情况，黑色实线为降雨量随时间变化的趋势线。吉林西部平原区年际降雨量变化规律，见图2。从图2棕色折线图可以看出：①吉林西部平原的降雨量年际间波动较为明显，最大降雨量为出现在1998年的622.64 mm；②最小降雨量为出现在1982的281.1mm。此外，由黑色趋势线可以看出，吉林西部平原的降雨量在1975-2015年间呈现逐年降低趋势，降低速率为0.32 mm/a。

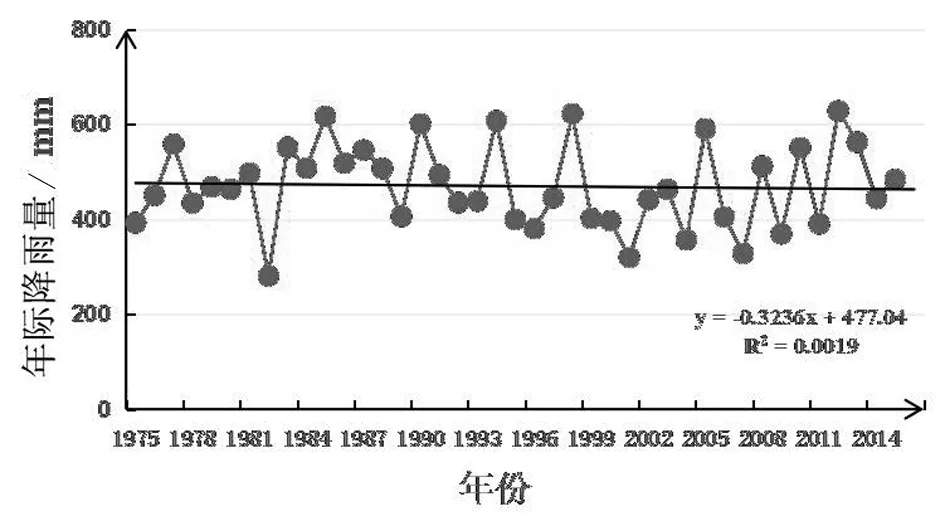
图2 吉林西部平原区年际降雨量变化规律

吉林西部平原区生长季降雨量变化规律，见图3。如图3所示，棕色折线图为41a间的生长季降雨量情况，黑色实线为生长季降雨量随时间变化的趋势线。从图3棕色折线图可以看出：①吉林西部平原的生长季降雨量年际间波动同样较为明显，最大降雨量为出现在1994年的574.25 mm；②最小降雨量为出现在1982年的238.4 mm。此外，由黑色趋势线可以看出，吉林西部平原的生长季降雨量在1975-2015年间呈现逐年降低趋势，降低速率为0.80 mm/a。

图3 吉林西部平原区生长季降雨量变化规律

年际和生长季降雨量箱型图，见图4。蓝色为年际降雨量箱型图，由图4可知：年际降雨量不存在异常值，非异常范围内数值在281.10-628.69，中位数为463.76，平均数为470.24，上四分位数为548.75，下四分位数为400.99。综合数据可以看出，年际降雨量很好的符合了正态分布，且呈现轻微右偏态。橙色为生长季降雨量箱型图，由图4可见，生长季降雨量同样不存在异常值，非异常范围内数值在238.40-574.25，中位数为413.79，平均数为420.41，上四分位数为473.04，下四分位数为363.67。综合数据可以看出，生长季降雨量同样很好地符合了正态分布，且与年纪降雨量相同，呈现轻微右偏态。

图4 年际和生长季降雨量箱型图

2.2 降雨量的空间特征分析

2.2.1 基于Kriging的年际降雨空间特征

基于IDW的年际降雨空间特征，见图5。由图5可以看出，吉林西部平原区的年际降雨量空间分布总体呈现东南高、西北低的态势。吉林西部平原区的年际降雨量被分为6个等级，以长春、四平附近为最高，在570.51-609.30mm；以通榆、乾安附近最低，在376.58-415.36mm范围。此外，由图5可知：西北部地区降雨量较为平均，跨度为2个等级；而东南部地区的降雨量则变化较大，跨越4个等级。

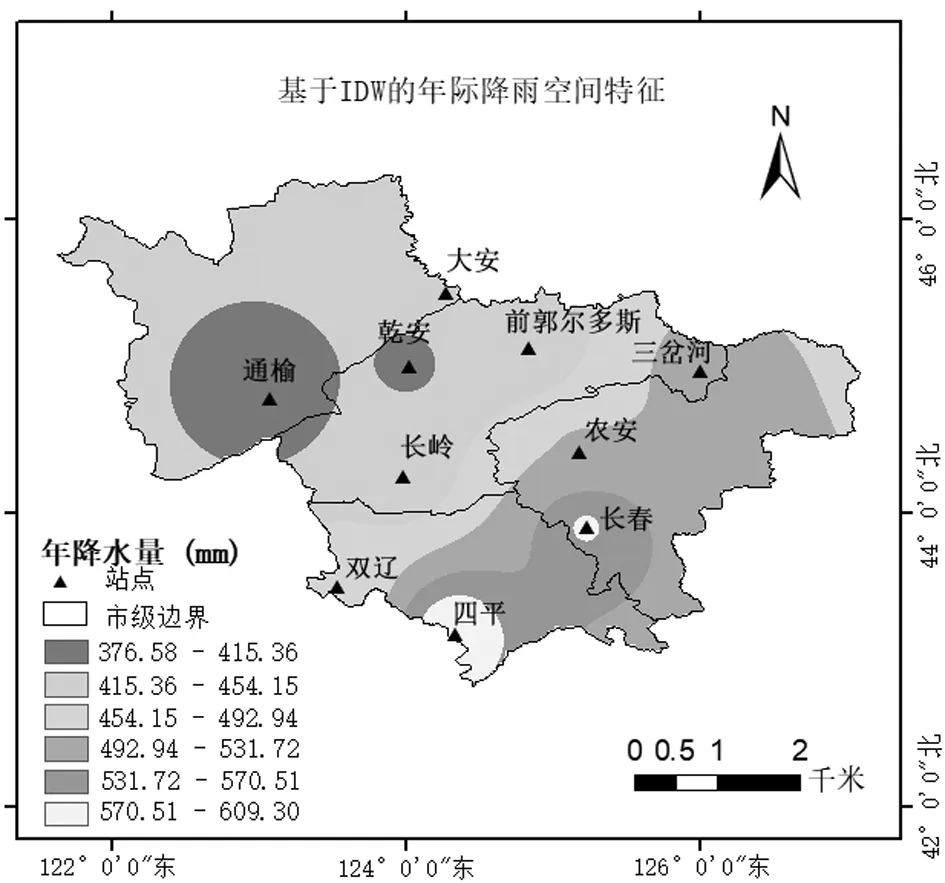
图5 基于IDW的年际降雨空间特征

与基于IDW的年际降雨空间分布类似，吉林西部平原区的生长季降雨量空间分布总体呈现东南高、西北低的态势。文章同样将吉林西部平原区的生长季降雨量分为6个等级，以长春、四平附近为最高，在497.85-528.02mm范围；以通榆、乾安附近最低，在347.00-377.17 mm范围。基于IDW的生长季降雨空间特征，见图6。与年际降雨量特征类似，西北部地区降雨量较为平均，跨度为2个等级；而东南部地区的降雨量则变化较大，跨越4个等级。

图6 基于IDW的生长季降雨空间特征

2.2.2 基于Kriging的年际降雨空间特征

基于Kriging的年际降雨空间特征，见图7。由图7可见：基于Kriging空间插值法的吉林西部平原区年际降雨量的空间分布，可以看出，年际降雨量同样呈现东南高、西北低的态势。此外，由图7同样可以发现在东南部降雨量分级跨度大于西北部，有4个降雨量等级集中分布于东南部，只有降雨量最低的两级分布于西北部。在年际降雨量被分为的6个等级中，长春、四平位于降雨量最高一级，在570.57-609.32 mm；通榆、乾安位于降雨量最低一级，在376.80-415.56 mm。

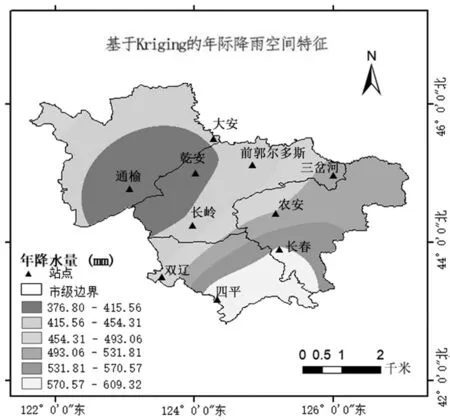
图7 基于Kriging的年际降雨空间特征

基于Kriging的生长季降雨空间特征，见图8。基于Kriging空间插值法的吉林西部平原区生长季降雨量的空间分布如图8所示，可以看出，基于Kriging法的吉林西部平原区生长季降雨量同样呈现东南高、西北低的态势。由图8同样可以发现在东南部降雨量分级跨度大于西北部，有4个降雨量等级集中分布于东南部，只有降雨量最低的两级分布于西北部。在年际降雨量被分为的6个等级中，长春、四平位于降雨量最高一级，在498.09-528.28 mm；通榆、乾安位于降雨量最低一级，在347.17-377.35 mm。

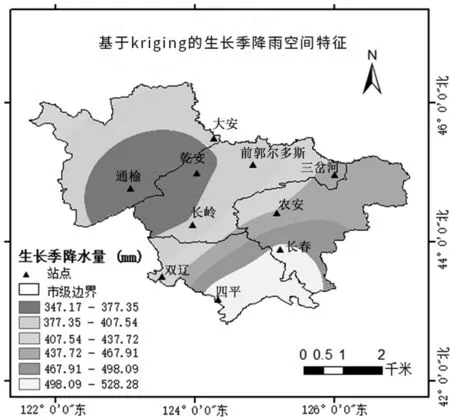
图8 基于Kriging的生长季降雨空间特征

通过对比基于IDW法所得的图5、图6与基于Kriging法所得的图7、图8，基于视觉效果可以得到以下结论：

1)Kriging法空间插值结果的不同降雨量分界线较为平滑，更为符合实际情况中降雨量的分布情况，而基于IDW法的空间插值结果则更接近于以站点为圆心的圆形组合，导致降雨量分布梯度边界更弯曲。

2)在通榆、乾安地区以及四平、长春地区可以看出，基于Kriging法空间插值结果中，通榆、乾安两地之间的区域降雨量和这两地在同一分级之中，四平、长春两地之间类似，而在基于IDW法的空间插值结果中，两地之间的区域则另属于一个分级，使得两地成为相互孤立的圆形区域。

这可能是由于Kriging空间插值法通过对整组空间数据点的关系来进行空间插值，不仅仅考虑插值点与实测点的空间相对关系，还考虑各临近点之间的位置关系，从而使插值结果更加真实、也更加客观。

2.3 误差分析

在ArcGIS中利用10个站点对吉林西部平原区内部年平均降雨量分别进行IDW法和Kriging法两种空间插值；然后，使用Extract Values to Points工具将空间插值所得的值赋予白城、双阳两个点位；最后，将空间插值所得降雨量与实测降雨量进行对比，检查站点降雨量实测值和计算值，见表2。白城站的IDW插值与实测值差异略小，说明IDW法插值所得结果在白城附近更为接近于真实值；而双阳站Kriging插值与实测值差异仅为IDW插值与实测值差异的1/2，说明Kriging法插值所得结果在双阳附近更为接近于真实值。

表2 检查站点降雨量实测值和计算值

MAE和RMSE计算结果，见表3。表3中所示为平均绝对误差(MAE)和均方根误差(RMSE)的计算结果，可以看出Kriging插值结果无论是MAE还是RMSE均

表3 MAE和RMSE计算结果

3 结 论

文章选取吉林西部平原区为研究区域，利用其内部共12个降雨量测量站点数据分析其降雨量的时空分布及演变特征。通过在年际和生长季两个时间尺度上，分析和评价IDW和Kriging两种空间插值方法在该地区的适用性研究，得出以下结论：

1)吉林西部平原区年际和生长季降雨量波动都很明显，年际和生长季降雨量降低速率分别为0.32 mm/a和0.80 mm/a，可以看出年际降雨量降低速率明显略低。

2)吉林西部平原区的年际降雨量和生长季降雨量的空间分布总体呈现东南高、西北低的态势。吉林西部平原区的年际降雨量生长季降雨量均以长春、四平附近为最高，以通榆、乾安附近最低。此外，西北部地区降雨量较为平均，跨度较小，而东南部地区的降雨量则跨度较大。

3)Kriging插值结果无论是基于MAE还是RMSE评价，其误差均