基于ARIMA模型的新能源汽车销量预测

缪辉 唐晨添 罗露璐

【摘 要】新能源汽车是近几年在汽車行业发展势头迅猛，其销量也反映出它的市场前景是一片大好，因此寻找一种准确简便的方法预测新能源汽车销量是十分必要的。文章选取了我国2014年1月至2019年5月新能源汽车月销量作为随机的时间序列数据，采用ARIMA模型对序列进行分析，同时建立最优且适合此序列的ARIMA模型对销量进行预测与对比，为新能源汽车行业的发展提供有益的参考。

【关键词】ARIMA模型;新能源汽车;预测分析

【中图分类号】F426.471 【文献标识码】A 【文章编号】1674-0688（2020）10-0097-02

0 引言

随着全球的环境问题和石油能源危机日趋严峻，世界各国都在积极采取相应措施实现经济的快速发展，新能源汽车的布局和发展已然成为世界各国汽车产业发展的重中之重。近几年，在全球环境问题日益严峻的形势下，各国积极改进技术研究环保节能汽车，新能源汽车就这样迅速地进入人们的生活。时下，占据大部分市场份额的为纯电动汽车和混合动力汽车，它们具有以下优点：①减少对石油资源的消耗和对环境的污染。②能源转换率高，使用成本低。③国内免征车辆购置税，上牌容易且无限行。为了节能减排，我国积极制定相关政策要求车企研究并生产新能源汽车，鼓励百姓购买新能源汽车。由于我国汽车厂商对新能汽车的研究与制造起步较晚，国内学者对这方面的研究也于近几年才逐渐兴起，对新能源汽车销量预测的研究也相对较少。针对新能源汽车发展趋势和市场销售的实际情况，建立销量预测模型有利于了解我国新能源汽车市场未来的需求，也能为相关学者的研究和汽车企业发展战略的制定提供参考。因此，有必要对新能源汽车销量进行预测研究。

近几年来，国内许多学者使用时间序列模型对汽车销量进行研究。例如，柳东威等人用时间序列法对2014年乘用车月销量进行预测[1];郭顺生利用时间序列模型预测汽车销量[2];凌拓对我国电动汽车市场销量进行研究[3];田锐锋用季节性模型预测“奥迪”汽车在华销量[4];王旭天等人运用SARIMA对我国汽车销量预测分析[5]等。综上可以看出，国内学者都采用了定量的预测方法，并且各位研究人员均取得了满意的研究结果。本文采用ARIMA模型实现对我国新能源汽车销量的预测。

1 模型概述

自回归移动平均模型通常简称ARIMA模型，该模型是由Box与Jenkins在20世纪70年代提出的，因此该模型通常也被称为box-jenkins模型，它是一种应用范围十分广泛的时间序列预测模型。ARIMA模型本质上是利用差分运算实现时间序列由非平稳化转换为平稳化，再利用因变量进行滞后值的回归拟合处理，基于模拟随机误差现值与滞后值进行模型的构建及回归模拟。本文以分析预测新能源汽车销量为例，运用ARIMA（p、d、q）（P、D、Q）模型对汽车销量月度数据进行分析预测。

2 ARIMA模型应用实例

2.1 数据来源及分析

本文数据来自中国汽车工业协会及知名汽车网站，选取了2014年1月至2019年5月的新能源汽车销量数据。新能源汽车的销量趋势和传统汽车销量趋势相近，每年的2～3月是销售的淡季，而10月～次年1月是销售的旺季。在具体预测过程中存在一定因素的影响，但在未来3个月时间范围内的销量预测还是能够有效地满足有关部门及市场的需要，同时在实际预测过程当中，政策的改变必然会造成销量的改变，因此主要是通过更新数据实现对预测结果的更新，超出3个月范围的预测结果不具有预测意义;本文在时间序列的基础上建立此模型，而时间序列来具有“近大远小”效应，预测时间如果超过要求，将导致精度有一定程度的降低。所以，本文预测的主要是最近3个月的销量情况，基于2014年1月到2019年5月的数据信息进行模型的构建，采用2019年3月到5月的数据进行模型验证。

2.2 时间序列平稳性分析

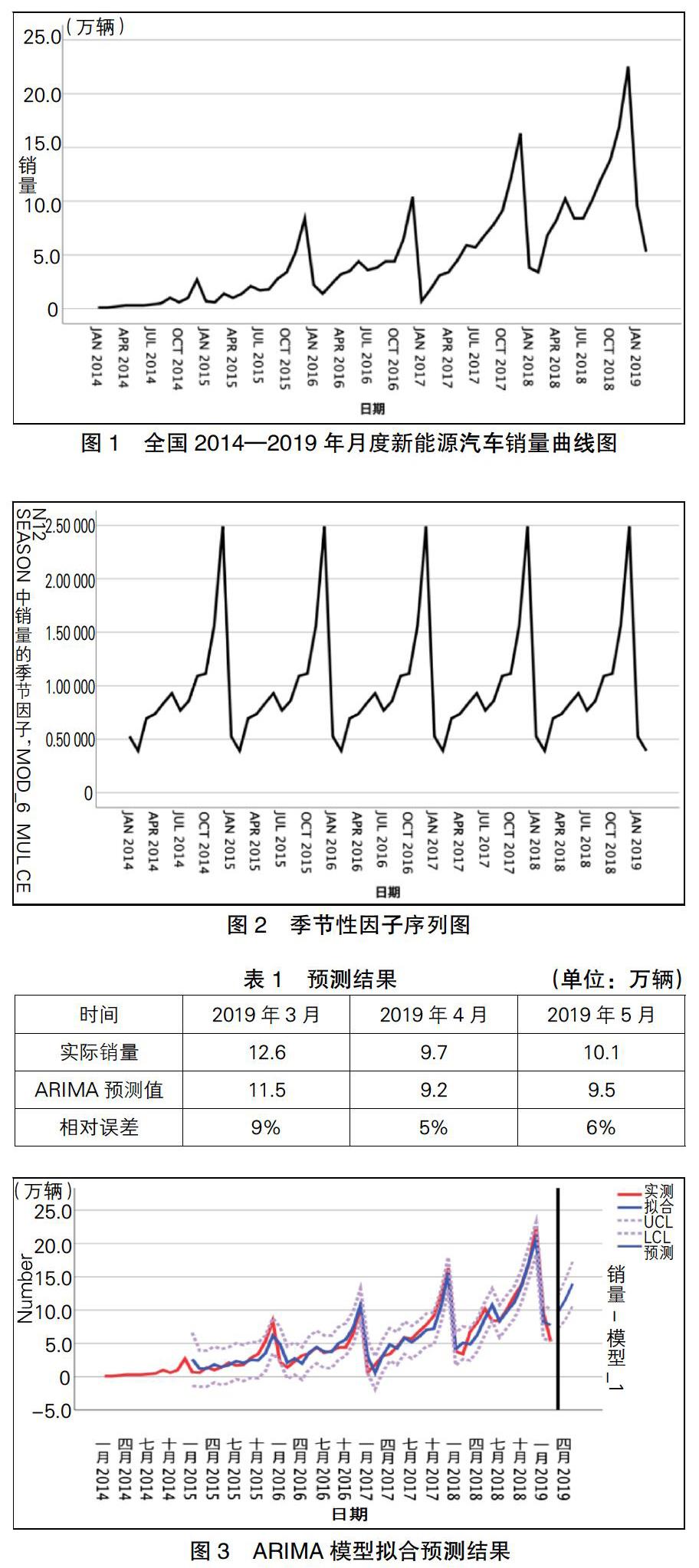
从图1可以看出，我国新能源汽车6年来的月销量呈现明显的变化趋势，上升趋势尤为明显，由序列图的分析可知，序列数据随着季节波动。由SPSS软件对数据进行季节性分解得到图2。

数据的非平稳性消除是必须先做的，按移位水平对某些异常离散值进行处理，之后进行差分处理，进行一次差分后的原始数据变为新的时序数据，同时逐渐表现出平稳性的基本特征，ADF单位根检验的新时序数据比较符合平稳性的要求，主要通过ARIMA模型开展相应的分析预测。

2.3 模型识别定阶及检验

这里的差分自回归移动平均模型包括6个参数：ARIMA（p、d、q）（P、D、Q），p和P表示自回归方程阶数;d和D表示差分次数;q和Q表示平均过程阶数。小写字母的p、d、q和大写字母的P、D、Q分别代表的是不包含和包含季节变动成分的ARIMA模型结果。因为本文是包含季节变动成分的时间序列，所以需看后面括号的结果。经过一次差分的时间序列，自回归过程阶数为1。

按照ACF和PACF（ACF是自相关函数，PACF是偏相关函数）分析原理开展相应的拟合过程，基于拟合的具体情况，最后取p=1，q=0，建立ARIMA（1，0，0）（1，1，0）模型的效果较为理想，并运用SPSS软件对AR（1）进行参数估计。

由模型输出参数发现：Sig<0.05，所以其建立的模型满足统计学要求，具有统计学意义。平稳R方为0.538，考虑季节变动的整体R方为0.932，证明SPSS软件自动计算生成的ARIMA（1，0，0）（1，1，0）模型的拟合效果是不错的。

2.4 模型拟合与预测

利用建立的模型对销量进行拟合及预测，结果见表1和图3。由图3可知，ARIMA（1，0，0）（1，1，0）拟合结果与实际销量趋势基本一致，但由于某些月份销量波动较大，例如2018年12月新能源汽车销量高达22.5万辆，而最低月份销量为3.4万辆，这就导致此模型在个别时段拟合与预测误差相对较大。ARIMA模型可以实现对销量趋势的有效预测，然而在极值处的预测误差有时会较大。

3 结语

本文选取的新能源汽车销量数据是近几年才开始统计的，导致只能对仅有数据的变化趋势进行分析预测，影响汽车销量的因素有很多，也较为复杂。时间序列分析的方法运用在此仅是一个大趋势的概括，有一定的局限性，例如只能对短期的数据进行较精确的预测，下一步可以考虑组合多种方法预测，效果可能更加理想。但从某些程度来说，此分析法概括的汽车销量变化的趋势较为有效，可将预测过程变得简单化。随着时间的推移，为了增加模型的精准和时效性，可以将旧数据不断更替为最新的销量数据。与此同时，应适当考虑时间序列和随机因素并增加样本，这样得出的结果可能会更优，而且预测精度会有所提高。预测新能源汽车销量的整体趋势是上升的，汽车厂商可以由此作为一定参考，合理调整产销计划，迎合国家优惠政策制定相关的销售方案，促进我国新能源汽车用户快速增长。就本文而言，采用的ARIMA模型拟合的不一定是最优的结果，但是就本文选取的新能源汽车销量数据来说，可能是最优的。

参 考 文 献

[1]柳东威，张海波，吴淑霞，等.基于时间序列法的2014年乘用车月销量预测[J].汽车工程师，2013（12）：13-14.

[2]郭顺生，王磊，黄琨.基于时间序列模型预测汽车销量研究[J].机械工程师，2013（5）：8-10.

[3]凌拓.我国电动汽车市场销量预测研究[D].重庆：重庆理工大学，2018.

[4]田锐锋.用季节性交乘模型预测奥迪汽车在华销量[J].统计与管理，2016（8）：70-71.

[5]王旭天，李政远，舒慧生.基于SARIMA的我国汽车销量预测分析[J].中国市场，2016（1）：71-74.