基于Abaqus仿真分析的某项目空气滤清器模态性能优化

白子琦 李光武

摘 要：汽车空气滤清器工作时，容易受到发动机等运动部件的激励，产生有害振动，传播辐射噪声。提升空滤的模态性能可以遏制振动与噪声的传播，一般情况下，主机厂要求空滤的一阶固有频率达到250Hz。文章以某车型空滤器性能优化为例，对空滤器进行了模态仿真，分析模态振型，通过调整上下壳体连接位置、合理布置加强肋、更改壳体材料等方法对空滤壳体模态进行了优化，使空滤器模态性能最终达到主机厂要求。

关键词：空气滤清器;模态分析;固有振动;固有频率

中图分类号：U464  文献标识码：A  文章编号：1671-7988（2020）21-46-03

Abstract： The air filter is easily affected by the engines excitation in its working process， which produces harmful vibrations and spreads radiated noise. Improving the modal performance of air filter can restrain the propagation of vibration and noise， generally， the manufacturer requires the first-order natural frequency of air filter to reach 250Hz. This paper takes the optimization of the air filter performance as an example， modal simulation of the air filter was carried out， the modal vibration mode was analyzed， and the air filter was optimized by adjusting the connection position of the upper and lower shells， reasonable arranging the ribs， and changing the air filter material to make the air filter modal performance finally reaches the requirements of the manufacturer.

Keywords： Air filter box; Modal analysis; Natural vibration; Natural vibration frequency

CLC NO.： U464  Document Code： A  Article ID： 1671-7988（2020）21-46-03

1 前言

空气滤清器作为进气系统的主要部件，其作用是过滤空气中的灰尘、杂质，為发动机内部燃烧提供纯净的空气。空滤器在工作过程中，壳体外部受到发动机振动的激励，内部受到高速气流的冲击，容易产生有害振动，从而影响空滤器的使用寿命，造成漏气、破裂、失效。

噪声和振动与壳体的模态性能有关，提高空滤的模态性能，使其固有频率远离发动机激励频率时，可避免共振现象的发生，抑制辐射噪声。本文以研究某车型空滤器结构和固有振动特性入手，对空滤器的初始设计进行模态仿真分析，并对空滤进行了结构优化、材料优化，使最终设计满足发动机要求，并对仿真结果展开了讨论。

2 空滤器模态分析理论

2.1 模态分析理论

模态分析[1]是一种研究结构动力特性的方法，应用振动理论求解结构的模态参数。每一阶模态都对应特定的固有频率、阻尼比和模态振型。求解空滤器自由模态时，不考虑阻尼的影响，系统的动力学方程可表示为：

式中：[M]为质量矩阵;[K]为刚度矩阵;方程的解为：

解得特征方程为：

根据此式可求得多个特征值ω及特征向量x，对应系统的固有频率值和各阶振型。模态优化的过程就是通过分析各阶振型，找出产品结构强度相对薄弱的位置并进行优化，使产品整体的固有频率达到要求。在振动系统中，低阶模态对系统的影响更大，进行模态分析时，重点研究空气滤清器的1～4阶模态的固有频率和振型。

2.2 空滤器模态要求

发动机[2]工作时，气流通过滤清器、进气管路到达节气门，节气门周期性的开启与闭合，使发动机气缸中的周期性压力脉动通过进气管路传递至空滤。为避免空滤受发动机激励形成共振，要求空滤的一阶固有频率需高于发动机的点火频率。发动机点火频率可通过计算获得：

式中：n为发动机转数;i为气缸数。

对于四冲程发动机，根据计算，得出发动机点火频率为200Hz。考虑到安全系数的影响，要求其滤清器的固有频率需达到250Hz。

3 空滤器有限元模型的建立

3.1 空滤器几何模型

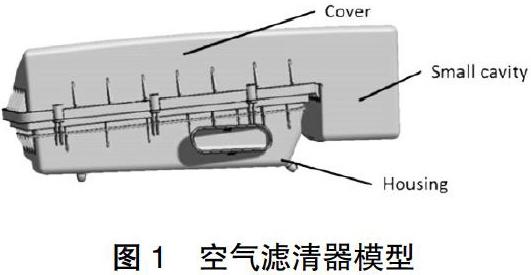
本文的研究对象为发动机顶置空滤器，其三维模型如图1所示。模型只包括空滤上壳体、空滤下壳体。做空滤模态分析时，一般不考虑内部滤芯的影响。

3.2 网格划分

模型前处理工作是仿真分析前的重要一步，网格质量的优劣直接影响计算结果的准确性。将空滤器三维模型导入Hypermesh软件中进行网格划分，按照模型结构特点，选择单元尺寸为2mm，在模型的表面上划分面网格，然后调整网格结构，使面网格满足网格单元质量要求;再根据四面体网格划分方法，利用面网格生成体网格。生成的体网格共计225010个节点，682951个网格单元。

3.3 参数设置及边界条件

空滤器上、下壳体材料初始为PP+TD20，该材料的弹性模量为2200MPa，密度为1.06e-9t/mm3，泊松比为0.38。约束上下壳体连接位置的6个自由度[3]，在Abaqus软件中设置，其中三个螺栓连接采用MPC约束方式，插接约束设置为Tie约束形式，建立好的有限元模型如图2所示。

4 空滤模态仿真及优化

4.1 空滤器结构优化及模态分析

将空滤器有限元模型导入Abaqus软件中进行计算，利用Lanczos算法提取空滤器前四阶模态，如图3所示，系统的1阶固有频率为160.97Hz，不满足高于250Hz的标准。根据初始状态的仿真结果，进行多轮方案优化空滤结构。

优化方案一：调整中间及最右侧卡接、螺接位置，使其更靠近小腔体。

方案一的修改变化如图4所示，上下壳体在空滤中间及最右侧卡接、螺接位置向小腔体位置移动。对方案一的模型进行模态仿真计算，仿真结果如图5（a）所示，从振型上看，相比于初始设计，上下壳体连接处靠近小腔位置的变形量明显减小。方案一的1阶固有频率为195.43Hz，相比于初始设计提升了37.36Hz。

优化方案二：在方案一的基础上，加密壳体外部的加强肋。

增加壳体上的加强肋，可以提高空滤整体的结构强度，且无需增加太多重量。方案二在方案一的基础上，增加壳体外部加强肋的数量，如图4所示。图5（b）为方案二的各阶模态振型，方案二的一阶固有频率为198.33Hz，相比于方案一，只提升了2.9Hz。

优化方案三：在方案二的基础上，在上壳体内部布置加强肋。

为消除上壳体顶部曲面的振动，在上壳体内部布置加强肋，其中，加强肋平均高度为14mm，厚度为1.5mm，加强肋之间间距为42mm，如图4所示。对方案三进行仿真分析，仿真结果如图5（c），可以看出，上壳体曲面振幅明显减小，方案三的一阶固有频率达到229.99Hz，相比于方案二，提升了31.66Hz。但方案三的一阶固有频率仍未达到目标高于250Hz，后续需进一步优化空滤壳体模态。

4.2 空滤器材料优化及模态分析

壳体材料对壳体模态性能的影响极大，一般情况下，材料的弹性模量越大，密度越小，壳体的模态性能越好。PP+GF30是一种常用的空滤壳体材料，其弹性模量为5800MPa，泊松比为0.4，密度为1.13e-9 t/mm3。本文在空滤器结构为方案三的基础上，提出三种材料方案优化壳体模态，分别为：

方案四：下壳体采用PP+GF30，上壳体为PP+TD20;

方案五：上壳体采用PP+GF30，下壳体为PP+TD20;

方案六：上、下壳体均采用PP+GF30。

对三种材料优化方案进行仿真分析，分析结果如表1所示，可以看出，方案五、方案六一阶固有频率满足发动机要求，考虑到PP+GF30的价格高于PP+TD20，减少制造成本，选择方案五为最终优化方案，方案五的一阶固有频率为283.52Hz。

5 结论

本文针对空气滤清器在工作过程中产生的振动与噪声问题，从壳体结构强度的角度出发，对滤清器的模态性能进行了仿真分析及优化。结果表明，合理设计上下壳体连接位置、在壳体上布置加强肋对空滤模态性能均有提升;又探究了壳体材料对模态性能的影响，将方案五：上壳体采用PP+GF30，下壳体采用PP+TD20材料选为空滤器最终方案，空滤一阶固有频率也从初始的160.97Hz提升至283.52Hz，优化后的结构满足发动机要求，优化设计为产品开发提供了可靠的依据。

参考文献

[1] 孟淼等.汽车空气滤清器的结构分析及优化[J].噪声振动与控制， 2016（4）.344-348.

[2] 郭付洋，陈剑.空气滤清器的声振耦合特性分析及优化[J].噪声振动与控制，2011（4）.169-172.

[3] 马春文.基于HYPERWORKS的空氣滤清器壳体模态分析方法[J].企业科技与发展，2014（10）26-27.