新型柔性导流坝下游断面水流分布特性试验
郭 婷,姚 宇,3*,刘 璟,李鑫斐,邓 斌,3,蒋昌波,3,唐梦君
(1.长沙理工大学 水利工程学院,长沙 410114;2.中交(天津)生态环保设计研究院有限公司,天津 300461;3.洞庭湖水环境治理与生态修复湖南省重点实验室,长沙 410114)
水生植物作为一种天然屏障,在护岸与水体修复等方面发挥出巨大的作用。而水流流态是影响水生植被存活与生长的重要因素。工程中常采用设置整治建筑物来改变水流特性[1-4],为坝后初生植物生长创造条件。因此如何有效地设计整治建筑物对于维护水体生态系统具有重要意义。
在整治建筑物对水流特性影响的研究中,对于刚性建筑物特别是丁坝的研究较为充分。例如:Tang等[5]采用大涡模型对丁坝影响下的流速、流线和涡流分布进行了模拟分析。Yazdi等[6]利用Fluent对不同流量、不同丁坝角度和长度影响下丁坝周围的流场进行了模拟研究。还有一些学者分析了不同形态的丁坝坝后的水流特性,如正态曲面形[7]和台阶式[8]。上述刚性整治建筑物虽然能取得较好的工程效果,但是需要大量的资本投资,而且对河道的水沙动力和生态环境具有负面影响,因此近年来学者们开展了柔性坝对水流特性影响的研究。如李怀恩等[9]通过野外试验,研究了沙棘柔性坝各种植参数对沟道水流水位及流速分布的影响。张鸿敏等[10]基于野外水流试验探讨在不同坡度条件下沙棘植物柔性坝对流速变幅值和水深沿程分布的影响。上述试验中对柔性坝的研究都是基于天然植物作为坝体,但对于某些难以定植的河流来说是不太可行的,可采用更易于稳固的柔性坝作为该类河流的整治建筑物。目前关于柔性坝的相关研究仅限于对柔性坝在不同流速下的运作机理和运作形态的研究[11],并未发现有学者对柔性坝影响下的流速分布开展研究。
因此本文拟采用一种新型柔性导流坝模型,该模型由柔性透水材料制作并采用了主坝和多个支坝相结合的设计,旨在改进植物因上层水流流速过大而倾伏于河底的缺点;通过水槽物理模型试验分析柔性导流坝模型下游断面的水流特性,有助于以有利于植被生长和恢复为目的优化柔性导流坝的设计,为水生植被修复工程提供一种切实可行的解决方案。
1 试验设置
本试验在长沙理工大学水利试验中心的长30 m、宽1.2 m、高1.2 m的全自动通用水槽中进行(图1-a)。根据江苏省无锡市某地现场的勘测资料,综合考虑多个河道原型中水深和流速等因素,按照Froude相似准则以1:3的长度比尺换算得试验水深与试验流速,如表1所示,并结合原工程实际投放效果与试验水深设计导流坝模型。模型由浮筒、矩形主坝和三角形支坝三部分组成(图1-b)。主坝和支坝均采用透水性良好的柔性聚乙烯格网制作(图1-c),多个支坝均匀等距排列缝制连接在主坝两侧,塑料浮筒安装在主坝上部,模型充分伸展时总高度为0.51 m。将整个模型用密集的螺丝钉固定在槽底,导流坝两侧先用铁杆固定,再用密封剂将边壁两侧间隙填塞。模型在沿流方向布置在水槽中段,以减小受到入流和出流口的影响,模型沿槽宽方向均匀布置于整个断面(图1-d和1-e)。沿水槽长度方向分别布置3个测量横断面,以主坝为原点位置,各试验横断面距离原点的位置分别为:1.3 m、2 m和3 m(分别标记为1#、2#、3#断面)。在每个横断面上均匀设置7条流速测量垂线,相邻垂线的间距均为0.15 m。对于单条垂线,以当前水面下0.04 m为起始位置,自上而下每隔3.5 cm布置一个测点,一条垂线上有10~16个测点。本试验中的流速测量采用声学多普勒三维剖面流速仪(ADCP),该仪器采样起始点位于探头以下4 cm处,测量精度为1 mm/s。为保证数据的稳定性与可靠性,试验中测量频率采用50 Hz,单点的测量时间为120 s。
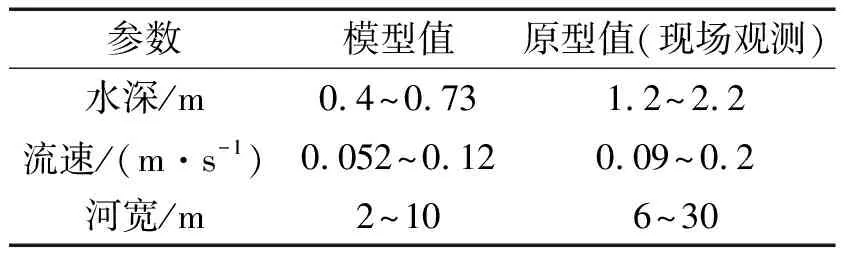
表1 河道的参数范围Tab.1 The ranges of stream parameters

图1 试验设置(单位:m)Fig.1 Experimental setup

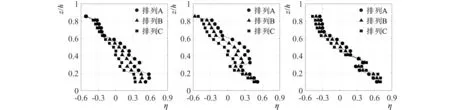
图2 模型排列方式Fig.2 Model arrangement
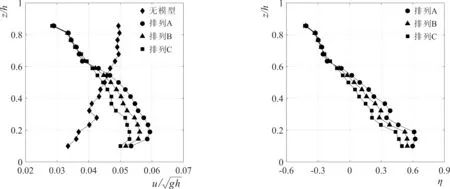
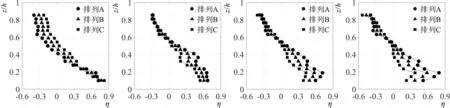
本文仅限于研究模型沿整个河流断面均匀布置的情况,因此并没有按比尺考虑河流的宽度(本试验的原型河宽为3.6 m,小于表1中现场观测的范围),但后述试验数据分析将证明水槽壁仅对近边壁的水流存在一定的影响。将试验静水深与模型总高度(浮筒加坝体)之比定义为相对淹没高度,本试验拟在表1所示的范围内测试3种水深(0.45 m、0.55 m和0.65 m,分别对应的相对淹没度为0.88、1.08和1.28)、3个入流流量(0.05 m3/s、0.075 m3/s和0.1 m3/s)和3种不同排列方式的柔性生态导流坝物理模型。模型在保持主坝与水流方向垂直的情况下,通过改变支坝末段的位置,使支坝与主坝的夹角分别为90°、60°和30°,对应排列A、B和C,阻水面积比A 水流在坝体存在的前后改变可由流速变化率η来描述,定义为η=(v2-v1)/v1,其中,v1为投放柔性生态导流坝前测点的流速,v2为投放导流坝后的流速。由上述定义可知流速变化率的值越小,模型对该测点的减速效果越好。图3-b展示了图3-a三种淹没度下有模型时的流速相对无模型时的减速率:在相对淹没度0.88和1.08工况下流速变化率较为接近,均大约以相对水深z/h=0.55为界,分界点以上断面平均流速变化率小于0,此时模型对水流具有减速效果,且该效果随着相对水深的减小而加强,在水面附近可以达到40%;由于整个断面流量守恒,在分界点以下则模型对水流具有加速效果,在水底附近水流加速了近80%;而在相对淹没度为1.28时情况则相反,以相对水深z/h=0.6为分界点,在分界点以下,断面平均流速变化率小于0,表现为减速,且减速效果随着相对是水深的增加而加强,并在z/h=0.3位置达到最强,近60%;在分界点以上则对水流具有加速效果,最大加速率约为60%。 3-a 无量纲水平平均流速(u/gh)3-b 流速变化率(η)沿相对水深(z/h)的分布图3 模型相对淹没度变化下3# 横断面上无量纲水平平均流速(u/gh)和流速变化率(η)沿相对水深(z/h)的分布Fig.3 Distribution of the dimensionless mean streamwise velocity and the velocity variation rate with the relative water depth (z/h) on the cross-section 3# under different relative model submergences 图4-a展示的是相对淹没度为0.88和模型支坝与主坝角度为90°(排列A)时,试验的三种入流流量下(0.05 m3/s、0.075 m3/s和0.1 m3/s)3#断面(对断面上7条垂向测线进行平均后)水平流速的垂向分布,并与无模型的情况进行的对比。从图4-a可以发现:相对于无模型的情况,有模型存在时三种入流流量下垂向水流结构均显著改变,断面平均流速除了底部边界层附近外均随着相对水深的增大而增加,这同样是由于2.1节所述的在淹没度0.88时上层水体由于受到浮筒的阻挡水流流速减小,此时断面要维持流量守恒则更多的水流需要通过下层透水性较好的坝体,因此下层水体的流速显著增大。对比不同的流量的结果发现:上层的水流流速较为接近,断面流量的差异主要通过下层流速差异的增大来实现;底部边界层附近存在一定的测量误差,特别是流量为0.1 m3/s时的近底位置处,这是因为流量较大时水流与模型支坝底部相互作用加强,导致水流更加紊乱。 图4-b展示了淹没度为0.88和模型支坝与主坝角度为90°(排列A)时,试验的三种入流流量下模型的断面水平流速相对无模型时的变化率。图中可以发现入流流量变化基本上不改变模型下游相对于无模型情况时流速的减速和加速效果:三种试验流量下流速变化率的垂向分布基本相同,流速变化率大致上均随着水深的增大而呈线性增长,并在大约相对水深z/h=0.5位置表现出从减速到加速的过渡;最大的减速率约为60%,发生在测量的最小水深z/h=0.85处,不考虑近底部的误差最大加速率约为60%,发生在测量的最大水深z/h=0.2处。 4-a 无量纲水平平均流速(u/gh)4-b 流速变化率(η)沿相对水深(z/h)的分布图4 入流流量变化下3# 横断面上无量纲水平平均流速(u/gh)和流速变化率(η)沿相对水深(z/h)的分布Fig.4 Distribution of the dimensionless mean streamwise velocity and the velocity variation rate with the relative water depth (z/h) on the cross-section 3# under different inflow rates 图5-a展示的是相对淹没度为0.88和水槽流量为0.05 m3/s时,模型支坝与主坝夹角不同的三种排列下(A、B和C)3#断面(对断面上7条垂向测线进行平均后)水平流速的垂向分布,并与无模型的情况进行的对比。从图4-a可以发现,测试的3种排列模型下游的水平流速垂向分布规律一致:断面平均流速随着相对水深的增加而增加,但在底部附近由于边界效应断面平均流速随着相对水深的增加而减小,其原因与2.1节相对淹没度为0.88时工况一致。对比3种模型排列方式下的流速发现:在相对水深z/h=0.6以上位置,3种排列相对无模型时对水流的阻流效果类似,因为主要是受浮筒的影响;在相对水深z/h=0.6以下位置,水流相对于无模型时均得到了加速,但是流速增加幅度随着主坝与支坝夹角的增大而增大,特别在相对水深z/h=0.2的最大流速位置,排列A(夹角90°)下的水平流速较排列C(夹角30°)下增大约15%。 图5-b展示了相对淹没度为0.88和水槽流量为0.05 m3/s时,3种排列下的断面水平流速相对无模型时的流速变化率。与图4-a流速的分布基本对应,3种排列下的流速的变化率均随着水深的增大而呈线性增长。在相对水深z/h=0.6以上时,3种排列的流速变化率相似,均表现为减速效应;在此水深以下时,流速变化率随着主坝与支坝夹角的增大而增大;在相对水深z/h=0.5以下时,模型的影响表现为加速;在相对水深z/h=0.2时排列A(夹角90°)达到的最大加速效果约为60%,排列C(夹角30°)约为40%,两者相差20%,而排列B(夹角60°)的加速效果始终介于二者之间。 5-a 无量纲水平平均流速(u/gh)5-b 流速变化率(η)沿相对水深(z/h)的分布图5 模型支坝与主坝的夹角变化下3# 横断面上无量纲水平平均流速(u/gh)和流速变化率(η)沿相对水深(z/h)的分布Fig. 5 Distribution of the dimensionless mean streamwise velocity and the velocity variation rate with the relative water depth (z/h) on the cross-section 3# under different angles between the main dike and the branch dike 6-a y/b=0.1256-b y/b=0.2506-c y/b=0.3756-d y/b=0.500 6-e y/b=0.6256-f y/b=0.7506-g y/b=0.875注:y为测线到水槽右边壁的距离;b为水槽宽度。图6 模型支坝与主坝的夹角变化下3# 横断面上各测线(y/b)的流速变化率(η)沿相对水深(z/h)的分布Fig.6 Distribution of the velocity variation rate with the relative water depth (z/h) for sampling profiles (y/b) on the cross-section 3# under different angles between the main dike and the branch dike 由于支坝角度变化后的模型排列B和C相对于水槽中心线不再对称,水流可能会受到水槽边壁的影响,因此有必要通过分析断面3#上各测线上流速的分布情况,来验证图5中采用各侧线平均后的垂线流速,作为断面流速代表的合理性。图6展示了与图5对应的工况下,3种模型排列下所有测线上的水平流速相对无模型时的流速变化率。对比3种模型排列下各测线上的流速变化率发现:仅在最靠近水槽两边壁的测线(y/b=0.125、0.750和0.875)时(y为测点到水槽右边壁的距离,b为水槽宽度),3种排列下的上层水流流速变化率表现出一定的差异;同时由于支坝偏向左岸,因此左边壁的这种差异更大;在靠近右边壁的y/b=0.125处时,减速率的幅值随着主坝与支坝的角度(从排列A到排列C)的减小而减小,在靠近左边壁的y/b=0.750和0.875处时,减速率的幅值随着角度的增大而减小,因此当对断面所有的测线进行平均时,这种差异会相互抵消,故对断面所有垂线进行平均后的水平速度变化率的垂向分布(图5-b)与靠水槽中间侧线上(y/b=0.250、0.375、0.500、0.625)的分布趋于一致,证明了本文选用断面所有垂线平均后流速来进行分析的合理性。 本文通过物理模型试验研究了一种主坝与支坝相结合的新型柔性坝下游水流的分布特性。试验分别测量了在不同淹没度、不同流量以及不同支坝角度组合下,坝后断面水平流速和相对于无坝时流速变化率的垂向分布,通过数据分析得到如下主要结论: (1)相对淹没度对水平流速的垂向分布影响十分显著:当相对淹没度较小时,水流主要通过下层的坝体透过,水体上层流速减小,下层流速增大,减速区在近表层;当相对淹没度为增大时,水流可翻越坝体通过,上层流速增大,下层流速减小,减速区在近底层。 (2)坝后断面水平流速的垂向分布规律受入流流量变化的影响不大,且垂线上各点的流速随着流量的增大而增加;断面流速变化率的垂向分布在3个流量级试验下趋于一致。 (3)主坝与支坝呈90°夹角时对坝后断面下层水流流速的垂向分布的改变最大,水流的变化率随着夹角的增大而增大。 断面上层水流的减小更适宜保护根系不着生于河床底部的浮游水生植被和漂浮水生植被;断面下层水流的减小则更利于保护根系固定于河床底部的挺水植物与沉水植被,因此实际工程中可根据当地主要水生植物的特性选择因地制宜的柔性坝布置方式。2 试验数据分析
2.1 相对淹没度对坝下游断面水平流速垂向分布的影响
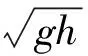

2.2 入流流量对坝下游断面水平流速垂向分布的影响

2.3 模型支坝与主坝的夹角对坝下游断面水平流速垂向分布的影响
3 结论

