线性经济模型换基迭代准则的研究
李永平
(天津财经大学理工学院,天津 300222)
一、引言
资源优化配置模型是经济优化决策的核心问题,也是决策的关键所在,特别是线性经济模型由于其结构简单、经济意义明晰、算法相对成熟,因此作为管理科学的基础理论—线性规划技术在实践中得以广泛应用。
对资源优化配置的线性经济模型,G.B.Dantzig的单纯形方法(Simplex method)在实践中证明是非常有效和普遍适用的,其基本的思想方法与步骤分为两个阶段:其一是寻找初始基可行解,对其进行最优性的判别,若是,则求解结束;否则,转入第二个阶段即换基迭代,得到使目标函数改进的下一个基可行解,对此基可行解置其为初始基可行解,即回到第一个阶段;如此循环,有限步迭代之后一定可以得到问题的最优解(或判定无最优解)。但在具体的换基迭代过程中,其进基变量的选择,通常选择检验数所对应的基变量xj为进基变量,这样的选择,一定可以使目标函数f 得以改进(特别是在非退化情形下,f的改进是严格增加的;在退化的情形下,它至少是不减的)。但我们经过认真研究发现它并不是当前状态下的最好的选择,在换基迭代时,如果在考虑λj的同时一并考虑xj的调整量θj,则可使目标函数得到更好的改进(即增加值更大),从而使迭代步骤有效减少,这一点,对大型的线性经济模型问题,有着十分重要的意义;同时,对一类退化的线性经济决策模型,可以避免迭代循环现象的发生。
二、问题及相关命题
(一)线性经济模型
一般地,在标准化意义下,基于资源优化配置的线性经济模型表述为:

其中,c=(c1,c2,…,cn),x=(x1,x2,…,xn)T

这里f 是目标函数,Am×n为技术系数矩阵,b 为可利用的资源数量,c 为产品的价格向量,且约定矩阵Am×n行满秩,以表明产品生产的m 种资源约束均为有效约束。
(二)典式及单纯形表



定理3 所表述的实际是问题(1)的换基迭代具体算法,在经过以上步骤后,实现了从可行基x0到可行基x1的转换。
在具体的模型求解中,为方便过程叙述与求解,将定理1、定理2、定理3 就基可解的判别、换基迭代等过程,归纳总结列于表当中,也就是通常说的单纯形(Dantzig)表。在具体计算过程中,当出现两个或两个以上的检验数λj>0 的情形,以往迭代的一般做法是:取其中最大的检验数λm+k[3]67:


由此,{p1,p2,…,pl-1,pl,pl+1,…,pm}向量组可由{p1,p2,…,pl-1,pm+k,pl+1,…,pm}向量组线性表示,另B为基阵,向量组{p1,p2,…,pl-1,pm+k,pl+1,…,pm}自然可由向量组{p1,p2,…,pl-1,pl,pl+1,…,pm}线性表示,因此两向量组可相互表示,为等价关系,由定理:等价向量组有相同的秩,{p1,p2,…,pl-1,pm+k,pl+1,…,pm}线性无关得证。
由所证第一、第二,参考定理3 的证明[1]30-33易得定理4。
需要指出的是:定理4 在实现一个基可行解到另一个基可行解迭代的同时,实现了当前状态下目标函数最大的增加值,是最优步长选择的迭代,较过去换基迭代方法减少一些迭代步骤,特别是当面临较大型的资源配置线性经济模型时,其优越性更加凸显;同时,在模型(1)的基可行解是退化情形下,可以避免原来换基迭代方法出现的循环情形。
三、算例分析
例1:求解下列问题:

解:引入松弛变量,将问题标准化,易得第一张单纯形表(见表1)。

表1


表2

表3
由表3 可知原问题的最优解是:

它经过3 次换基迭代,而如果按原来的做法,则需要4 次换基迭代(因篇幅所限,具体做法这里略去)。
下面再举一例,这是1955 年,由著名数学家E.Beale 所提出的一个退化的、换基迭代出现循环的线性经济模型的经典范例。
例2:求x1,x2,…,x7满足:

在这个例中,有一个明显的可行基{x5,x6,x7},而且这是一个退化的可行基,从这个基开始进行迭代,在迭代过程中,当有几个λj同时是正时,选λj绝对值较大的列对应的变量作为换入变量。如果有几个基变量同时使θ 达到最小,就取下标较小的那一个作为换出变量。可以发现经过6 次迭代后,又得到了最初的可行基{x5,x6,x7},即出现循环,这样下去永远不会得到最优解[1]53-56。它表明对退化的线性经济模型问题用定理3 的方法进行迭代计算,有可能因出现循环而得不到结论。当然,避免循环以求解线性经济模型有摄动法和字典序方法,这里,针对例2采用定理4 之方法就可以避免其出现循环,且只需迭代2 次即得最优解。具体迭代过程,列于表4、表5、表6 中(表中带星号的数是迭代选定的枢纽元素)。
由表6 可得:例2 的最优解为:

最优值为:

四、结论与展望
以上我们讨论了有关资源配置的线性经济模型Dantzig 的换基迭代算法,并作了一点的改进,通过实例计算它是有效的。但就算法而言,由于面临现实问题的复杂性、多样性与特殊性,任何一种算法都只能是相对有效的,表现为“此优彼劣”,不可能“一劳永逸”解决所有的问题。“没有最好,只有更好”,在此,我们抛砖引玉期待有更好的算法以丰富与完善线性规划技术,为经济优化决策、为经济过程的定量化分析提供更有效也更有力的工具。

表4
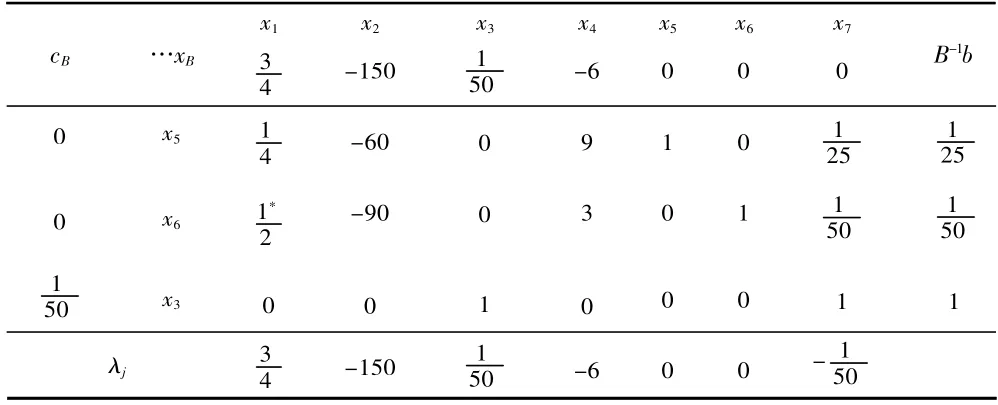
表5

表6

