稀土镁合金热变形行为和组织演变研究

王艳彬，陈文，黄少东，胡传凯，吴洋，夏祥生

（中国兵器工业第五九研究所，重庆 400039）

随着节能减排、减重增效任务的日趋严峻，汽车、电子及国防军工行业对轻质高强的镁合金构件提出了紧迫需求[1—3]。目前，商用的AZ 和ZK 等镁合金体系的性能提升基本已达极限，但还是不能满足装备轻量化对轻质高性能镁合金的现实需求[4]。Mg-RE 系镁合金具有优良的室温和高温力学性能，在轻型装备上应用的潜力巨大[5—9]，为节约材料成本，主要采用的方式一是降低稀土元素含量，二是以Mn 元素代替常用昂贵晶粒细化元素Zr，因此，开发了4Gd-2Y-1Zn-0.5Mn 合金，但对于该合金，其变形机理及变形特性尚不明确，这对合金的成形方案设计、设备选型和变形参数设计提出了挑战，因此，开展该合金的热变形行为及组织演变研究，为该合金成形方案设计、设备选型和变形参数设计提供一定的理论方法和实验依据。

1 试验材料及方法

采用中频感应熔炼炉进行合金熔炼，首先在铁坩埚中将纯镁、纯锌和镁锰中间合金熔化，待温度稳定在780 ℃时加入Mg-30Y 和Mg-30Gd 中间合金，搅拌静置后进行半连续铸造，车去铸锭外皮，铸锭最终尺寸为Φ80 mm×3000 mm，合金的具体成分为Mg-3.94Gd-2.0Y-0.78Zn-0.56Mn（质量分数）。

在Gleeble3500 热模拟机上进行单向压缩试验，变形温度为350～500 ℃，变形速率为0.0005～0.5 s−1，变形量为60%（真应变0.91），首先将试样加热到指定温度，并保温2 min，压缩试验完成后，立即水淬。显微组织取自于压缩试样的心部，观察面平行于压缩方向，腐蚀液为体积分数为4%的硝酸酒精溶液。

2 结果及分析

2.1 流变应力特征

图1 所示为合金的应力-应变曲线。可见，其主要特征有：①在所有变形条件下，随着应变的增加，流变应力先急剧增加，然后随着应变的增加，流变应力增加速率放缓，到达峰值应力后，随着应变的增加，应力逐渐降低；② 当变形速率恒定时，随变形温度的升高，应力逐渐降低；③当变形温度恒定时，随变形速率的升高，应力随之升高；④ 在低温高应变速率条件下（300 ℃/0.05 s−1和0.5 s−1），试验发生了断裂，这主要是因为在低温下变形，滑移系少，不能协调晶粒之间的变形而发生早期断裂。

图1 合金的应力-应变曲线Fig.1 Stress-strain curves of alloy

2.2 热变形参数对流变应力的影响

2.2.1 变形速率对流变应力的影响

通过对多种材料高温热变形数据的分析表明，在低的应力条件下，指数关系可用来描述流变应力σ、应变速率和变形温度T之间的关系[10—11]：

式中：A1，n1为材料常数。

在高的应力条件下，幂指数关系可用来描述流变应力σ、应变速率和变形温度T之间的关系：

式中：A2，β为材料常数。

指数关系和幂指数关系描述了硬化和软化的动态平衡，这与稳态变形所对应的关系非常相似，因此，Sellars 等提出了一种修正的Arrhenius 函数来描述流变应力σ、变形速率和变形温度T之间的关系[12—13]：

式中：A，α和n为材料常数，其中α=β/n1；T为热力学温度（K）；Q为变形激活能；R为气体常数。

对式（1）和式（2）两边取自然对数，可以得到：

取合金不同速率下的峰值应力为流变应力，将数值分别带入式（4），作关系曲线，并进行线性回归，结果如图2 所示。根据式（4），取图2 中直线斜率平均值并取倒数得n1=9.541。

图2 lnε˙与lnσ 的关系Fig.2 Relationship between lnε˙and lnσ

同理，取合金不同速率下的峰值应力为流变应力，将数值带入式（5）中，作关系曲线，并进行线性回归，结果如图3 所示。根据式（5），取图3 中直线斜率的平均值并取倒数得β=0.129，结合n1数值，可得：α=β/n1=0.013。

假定变形温度对激活能的影响不大，对式（3）两边分别取对数得：

图3 lnε˙与σ 的关系Fig.3 Relationship between lnε˙and σ

将α值代入式（6），作lnε˙-ln[sinhασ]的关系曲线，并进行线性回归，结果如图4 所示。可见，合金流变应力和变形速率的双曲对数具有线性关系。

图4 ln[sinh α]σ 与lnε˙的关系Fig.4 Relationship between ln[sinhα ]σ and lnε˙

2.2.2 变形温度对流变应力的影响

变形温度对镁合金的流变应力影响较大，一方面是由于镁合金柱面和棱面滑移系的分切应力与变形温度有关，随着温度的升高，柱面和棱面滑移系易启动，合金的塑性变形能力增强，导致流变应力下降；另一方面镁合金在高温条件下变形易发生动态再结晶，降低变形过程中的加工硬化，从而使流变应力降低。

在热变形时，变形速率受到热激活的控制，可引入因子Z来表示变形速率和温度对应力的影响[14—15]：

根据式（3），可得到：

当变形速率一定时，假定变形温度对激活能的影响不大，对式（8）两边分别取对数得：

取合金不同速率下的峰值应力为流变应力，将数值分别带入式（9）中，作1000/T-ln[sinh]关系曲线，并进行线性回归，结果如图5 所示。可见，流变应力的双曲正弦对数与变形温度的倒数之间满足线性关系。

图5 ln[sinh ασ]与1/T 的关系Fig.5 Relationship between ln[sinh ασ] and 1/T

2.2.3 合金的本构方程

从以上分析可知，高温塑性变形时，合金的流变应力、变形速率和变形温度之间满足双曲正弦函数关系，根据式（3），只要求出合金的材料常数A，α，n，Q，即可得到合金的本构方程。本节采用 Z参数法来求解变形激活能等材料常数，根据式（3）可得：

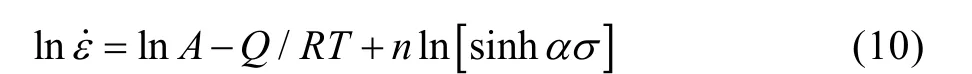
假定变形温度对激活能的影响不大，对式（10）两边分别取对数得：

对于常数A，将Q 值代入式（8），可得到Z 和ln Z 的值，根据式（9），作ln[sinh ασ]-ln Z 关系曲线，并进行线性回归，结果如图6 所示。可见，两者在试验速率和温度范围内符合线性关系，其中ln[sinh ασ]-ln Z 关系曲线的斜率为n 值，而其截距为ln A 值，从而求得常数的数值为：A=3.704×1021，n=6.309。

综上分析，可得到合金的本构方程为：

图6 峰值应力与Z 参数的关系Fig.6 Relationship between peak stress and Z parameter

2.3 变形条件对显微组织的影响

2.3.1 变形温度对显微组织的影响

图7 所示为合金在变形速率为0.0005 s−1条件下不同变形温度的显微组织，由图7 可见，当在350 ℃变形时，原始的大晶粒沿垂直于压缩方向被严重拉长，在晶粒的晶界周围可以看到许多的小晶粒，在此条件下试样内部发生了动态再结晶，但小晶粒所占的比例较少，说明动态再结晶不完全，显微组织由晶界的小晶粒和原始的大晶粒共同组成，呈现为混晶组织，如图7a 所示；在变形温度为400 ℃时，合金的小晶粒所占的比例相对于350 ℃变形时有所增大，说明升高温度有利于再结晶比例的提高；继续升高变形温度到450 ℃，再结晶比例进一步增大；当变形温度为500 ℃时，显微组织全部由再结晶晶粒所组成，发生了完全再结晶。由此可以看出，当其他变形条件一样的情况下，在高温区变形有利于得到完全的再结晶组织。

由上述分析可见，变形温度能显著影响稀土镁合金组织形态，形变温度较低时，稀土镁合金中可开动的动滑移系较少，形成少量位错，相互作用几率减少，难以形成有效的位错塞积，导致再结晶形核率低；升高变形温度，位错的形成与运动过程中，易于增殖和产生相互作用，形成具有高位错塞积的畸变区，增大再结晶的形核率。温度升高同时会引起再结晶晶粒尺寸变大，合金在0.0005 s−1条件下不同变形温度的再结晶晶粒尺寸如图8 所示，可见在350 ℃变形时，动态再结晶晶粒尺寸在1.2 µm 左右，当在500 ℃变形时，动态再结晶晶粒尺寸在51.3 µm 左右。由此可以看出，虽然在高温区变形有利于得到完全的再结晶组织，但晶粒长大也比较明显，在变形温度选择时还需与其他变形参数匹配选择。

图7 合金在0.0005 s−1 条件下不同变形温度的显微组织Fig.7 Microstructures of alloy at different deformation temperatures at 0.0005 s−1

图8 合金在0.0005 s−1 条件下不同变形温度的再结晶晶粒尺寸Fig.8 Recrystallized grain size of alloy at different deformation temperatures at 0.0005 s−1

从图7 的分析发现，在400 ℃和450 ℃中温区变形时，晶粒之间的衬度明显不同，再结晶区为亮色，而原始大晶粒内部呈灰色，进而对灰色区域进行了高倍观察，结果如图9 所示，可见，灰色区域由针状的LPSO 相组成，从图7 也可发现，该相的出现与变形温度有直接的关系，在低温下该相析出较为困难，在中温区原子的热激活加剧，原子的热扩散加强，而且溶质原子在微区存在过饱和的状态，使其易于析出，而在高温区（变形温度为500 ℃），其在基体的固溶度较大，析出得到了抑制。

图9 变形温度为400 ℃、变形速率为0.0005 s−1条件下的高倍显微组织Fig.9 High magnification microstructure deformed at 400℃/0.0005s−1

2.3.2 应变速率对显微组织的影响

图10 所示为合金在变形温度为500 ℃条件下不同变形速率的显微组织，由图10 可见，变形组织同样受到变形速率的显著影响。当变形速率为0.0005 s−1时，组织为完全的动态再结晶组织，晶粒尺寸较大，随着变形速率的升高到0.005 s−1时，显微组织也为完全再结晶组织，继续升高变形速率，动态再结晶比例逐渐减小。

图10 合金500 ℃条件下不同变形速率的显微组织Fig.10 Microstructures of alloy at different strain rates at 500 ℃

在高变形速率下变形时，位错在晶界等位置急剧塞积，形成高畸变能区，为再结晶形核提供必要的能量，并且变形速率高，作用时间短，动态再结晶晶粒形核后的长大受到了抑制，组织表现为晶粒尺寸差别大。合金500 ℃条件下不同变形速率的再结晶晶粒尺寸如图11 所示，可见变形速率越高，动态再结晶晶粒尺寸越小，在0.0005 s−1变形时，动态再结晶晶粒尺寸在51.3 µm 左右，当在0.5 s−1变形时，动态再结晶晶粒尺寸在11.0 µm 左右。由此可以看出，虽然高变形速率有利于获得细小的再结晶晶粒，但与此同时，其再结晶比例也相对较低。

图11 合金500 ℃条件下不同变形速率的再结晶晶粒尺寸Fig.11 Recrystallized grain size of alloy at different strain rates at 500 ℃

3 结论

通过热模拟试验研究了Mg-3.94Gd-2.0Y-0.78Zn-0.56Mn（质量分数）合金的高温变形特性，建立了基于修正的Arrhenius 方程，并分析了变形条件对显微组织的影响，得出以下结论。

1）当变形速率恒定时，随变形温度的升高，应力逐渐降低，当变形温度恒定时，随变形速率的升高，应力随之升高，在低温高应变速率条件下（300 ℃/0.05 s−1和0.5 s−1），试验发生了断裂。

2）合金高温压缩变形时，峰值应力和应变速率、ln[sinhασ]与1/T之间满足线性的关系，根据线性拟合，求得合金的材料常数，基于修正的Arrhenius方程获得了合金的本构方程为1021[sinh 0.013σ]6.309exp(-324 619/RT)。

3）当变形速率一定时，随着变形温度的升高，合金的动态再结晶比例逐渐提高，而再结晶晶粒尺寸也逐渐增大，在变形速率为0.0005 s−1变形时，当变形温度从350 ℃增大到500 ℃时，动态再结晶晶粒尺寸从1.2 µm 增大到51.3 µm。

4）当变形温度一定时，随着变形速率的升高，合金的再结晶比例逐渐降低，而再结晶晶粒尺寸也逐渐减小，在变形温度为500 ℃变形时，当变形速率从0.0005 s−1增大到0.5 s−1时，动态再结晶晶粒尺寸从51.3 µm 减少到11.0 µm。