基于改进迭代贪婪算法的预制构件调度研究

陈竑翰，熊福力，曹劲松，李 志

(西安建筑科技大学 信息与控制工程学院，西安 710055)

0 引言

在混凝土预制构件生产的系统中，利润最大化是企业的首要目标。决策者需要根据两个重要的约束条件，即企业生产能力约束和交货期约束，在两个约束条件下会迫使企业来决定是否接受或拒绝哪些候选订单以及如何对订单进行安排。这种问题被称为订单接受与调度问题(order acceptance and scheduling, OAS)[1]。

有许多精确的方法被用来解决小规模的OAS问题，例如分枝定界算法[2]和动态规划算法[3]。目前已经证实流水车间的OAS问题属于NP-hard问题[4]，所以当问题规模过大时为了在合理的计算时间内获得近似最优解，一些学者提出了有效的启发式算法[5]和元启发式算法[6-7]进行求解。郑凡等[8]针对订单接收的流水车间调度问题，提出了一种并行变邻域搜索算法,采用双串表示方法、新型的邻域结构和并行搜索机制解决了该问题。Wang等人[9]考虑了模具制造、预制构件储存和运输的影响，以最小化延迟和早期惩罚的总成本，并通过GA解决了这一调度问题。Prata[10]考虑了铸梁模具有效生产能力的约束条件，并采用整数线性规划方法来最小化订单生产损失。Ko等人[11]讨论了相邻工序之间带缓冲区容量的预制调度问题，并通过GA进行求解。

目前在预制构件的生产中还未对OAS问题进行过研究。因此，本文以最大化总净收益为目标，提出了一个预制流水车间的OAS模型。针对此模型本文设计了一种改进的IG算法。在改进的IG算法中，在重建过程之前加入了一种构造启发式的规则，并且结合阈值接受算法设计了一种自适应接受准则。最后将改进的IG算法与禁忌搜索算法、遗传算法以及经典IG算法进行了对比分析。结果表明改进的IG算法能获得更好的效果。

1 问题描述

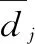
在生产过程中需满足以下条件：1)相邻工序之间工件的安装时间和运输时间可忽略不计;2)每道工序一次最多只能处理一个工件；3)每个工件一次最多只能在一道工序上处理；4)工件在工序上处理完成之前不能被其他工件抢占。

2 生产调度模型

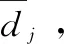
(1)

订单j的拖期时间Tj和完工时间Cj可由以下约束计算。

(2)

(3)

(4)

(5)

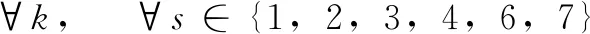
(6)

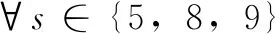
(7)

xj∈{0, 1}∀j

(8)

yj,[k]∈{0, 1}∀j,k

(9)

其中:式(2)和(3)表示每个订单的拖期时间的约束，式中Ω是一个大数；式(4)确保将每个接受的订单分配到一个位置，式中[k]表示订单序列的位置指标；式(5)表示每个位置只能分配一个订单；式(6)表示预制供应链环境下连续工序的完工时间,式中C[k]是指在第k个位置上订单的完工时间,pj,s是指订单j在工序s上的处理时间；式(7)表示预制供应链环境下并行工序的完工时间。式(8)和式(9)表示变量xj和yj,[k]均为二进制变量，若订单j被接受，xj取1，否则为0；若订单j分配到了订单序列第k个位置，yj,[k]取1,否则为0。

3 改进迭代贪婪算法

迭代贪婪(iterative greedy，IG)算法最初是由Ruiz[12]提出的，是对贪婪搜索方法的一种扩展。经典IG算法主要由两个主要阶段构成，一个是可行解的破坏阶段，另一个是可行解的重建阶段。在破坏阶段中，从完整的可行解中删除一些元素。然后在重建阶段通过应用一些贪婪规则重新构成一个完整的可行解。最后对完整的可行解进行选择性接受。由于其在调度问题上良好的寻优能力，目前它已在许多领域得到了广泛的应用。本文在结合预制构件订单接受与调度问题的基础上提出了一种结合构造式启发规则的带阈值接受的迭代贪婪算法(iterative greedy with threshold acceptance，IGTA)，以下各节详细介绍了IGTA算法的主要过程。

3.1 编码方式

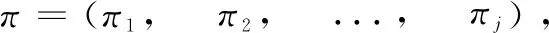
3.2 基于构造启发式的破坏-重建策略

在经典IG算法中的破坏-重建阶段中分为两个主要过程，首先在破坏过程中，从当前解中随机选择g个订单并将其移除，然后可以得到两组序列，一组是由剩余的订单组成的部分序列，另外一组是有移除的订单组成的部分序列，其中，移除订单数即破坏因子g通常在(2，3，...，8)中取值；其次在重建过程中，将移除订单组成的部分序列从左至右逐一插入所有的位置，并进行比较，最终将订单插入是目标值增加最多的位置，从而可以得到一个当前最优解。

从经典IG算法中可以看出，重建过程直接对剩余订单序列进行插入操作，并未充分利用剩余订单集合中交货期、处理时间以及最大净收益等信息，很可能导致求解质量下降。因此，为了在调度序列重建过程中有效改善目标值，本文结合预制构件订单接受与调度问题数据信息，提出了一种基于构造启发式规则的重建操作策略，如图1所示，首先利用公式(10)在剩余订单集合中对ξj进行递减排序，然后再从移除订单集合中逐个抽出订单，并插入到使得总净利润最小的剩余订单序列位置，直到移除订单集合中没有订单。

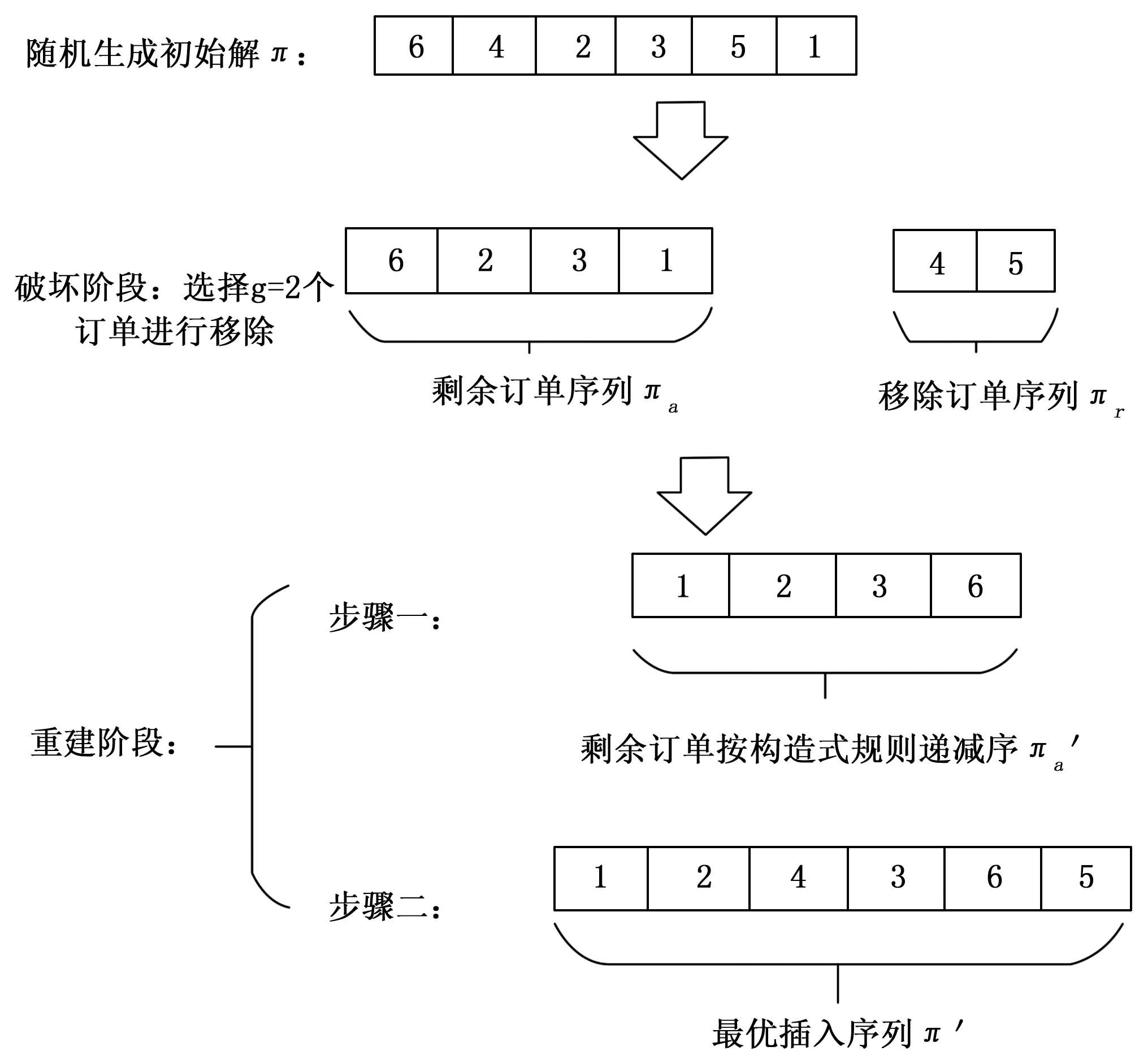
图1 基于构造启发式规则的破坏-重建策略图

(10)

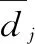
3.3 局部邻域搜索

本文中的邻域搜索方法采用是一种插入式的局部邻域搜索方法。其基本思想是：每次从当前解中随机地选择一个订单，将订单从左至右逐一试插，最终将订单插入是目标值增加最多的位置。如果通过邻域搜索找到的新解优于当前解，则对当前解进行替换并继续搜索，否则就结束搜索。

3.4 阈值接受准则

经典IG算法中的接受准则是基于模拟退火算法中的按概率接受新解作为当前解。为了帮助IG算法能够拥有更好扰动性能，并能更加容易跳出局部最优，本文通过结合一种阈值接受算法，提出了一种新的阈值接受准则。阈值接受算法是对模拟退火算法的改进，它是使用阈值对整个求解过程进行控制。阈值接受准则能够使IG算法在一定范围内接受稍差的解，从而使算法跳出局部最优值，与模拟退火算法中的接受准则相比，阈值接受准则能进行更小范围内的搜索[13]。

在本文中，为了综合考虑订单规模和优化效率，初始阈值设置为T0=n2，其中n表示订单数；阈值衰减系数α是随着迭代次数Iter不断进行变化的一个自适应值，由式(11)确定。

(11)

3.5 终止条件

本文中提出的IGTA算法为了综合考虑问题的规模，且保证算法充分收敛情况下，设定终止条件为10*n2毫秒的程序运行时间。其中，n为待决策订单的数量。

IGTA算法的伪代码如算法1所示。

算法1：IGTA算法伪代码

1:输入初始可行解π ，初始目标值f (π)

2: 设置算法参数，其中包括：移除订单数g以及初始化阈值T0；

3: 设定初始解为当前最好解 π*← π

4: while 不满足结束条件 do

5: 令 π’← π，flag=1, Iter=1，利用式(11)计算α;

6: for i=1 to g do

7: 从π’中随机选择一个订单移除，并将其置入移除订单集，组成剩余订单序列πa和移除订单序列πr；

8: end for

9: for i=1 to g do

10: 通过公式(10)中的构造式规则对剩余订单序列πa进行递减排序优化得到πa’ ；

11: 从移除订单序列πr中选择一个订单将其插入πa’中所有可能位置中能使目标增加最多的位置，得到最优插入序列π’；

12: end for

13: while flag=1 do

14: flag=0

15: for i=1 to n do

16: 从π’中不重复地随机移除一个订单并将其插入π’所有剩余位置中的最优位置，得到邻域搜索解π’’；

17: if f(π’’ )>f(π’ ) then

18: π’ ←π’’, flag=1;

19: end if

20: end for

21: end while

22: if f(π’’ )>f(π) then

23: π ←π’’

24: if f(π)>f(π*) then

25: π*←π

26: end if

27: elseif (f(π )-f(π’’ ))<α×T0then

28: π←π’’

29: end if

30: end while

31: return π*

4 实验结果及分析

本节根据所研究问题的特点设计了仿真实验，分析了本文所提出算法对不同问题规模求解的效果，并通过与禁忌搜索算法(tabu search，TS)、遗传算法(genetic algorithm，GA)以及经典IG算法进行比较，对算法的鲁棒性和求解质量给出分析结果。

4.1 测试实例

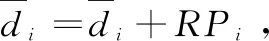
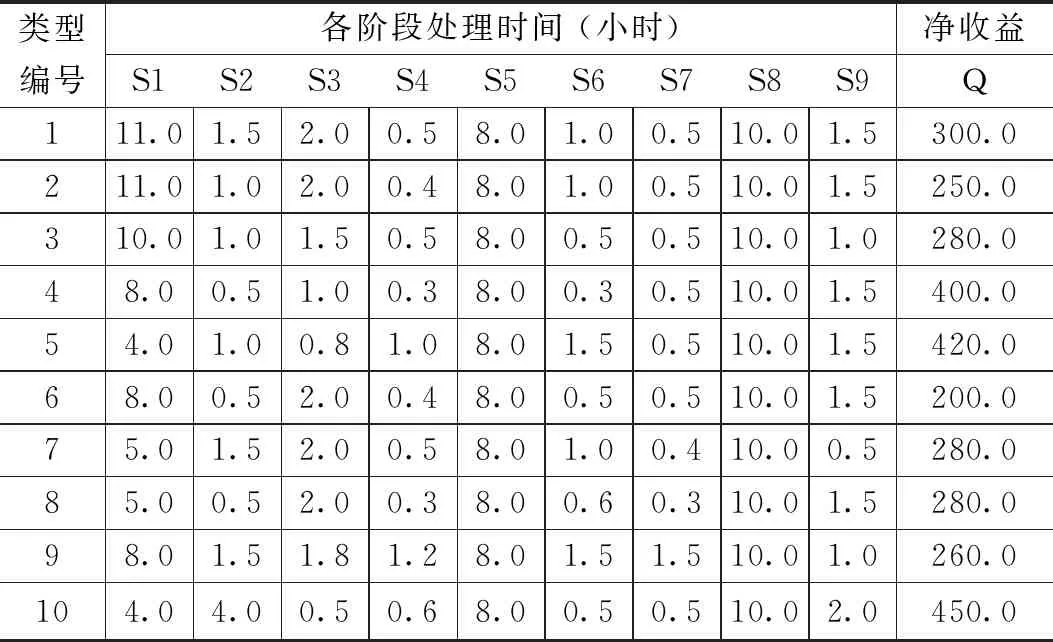
表1 生产数据

4.2 仿真结果与分析

所有实验均通过Matlab 2017b编程实现，并在计算机配置为Microsoft Windows 10，处理器为Intel Core i5-6300HQ CPU @ 2.3 GHz，8 GB RAM的个人电脑上运行。本文针对订单n为20，40和60的3种小、中、大规模的问题测试实例在实验中使用了禁忌搜索算法，遗传算法以及经典IG算法和本文所提出的IGTA算法进行对比，它们将在每个问题实例下进行30次测试。总计运行3 240(27×30×4)次。在本文中GA算法中的种群数量，交叉率和变异率分别选取为Ps=100，Pc=0.8，Pm=0.02；TS算法中的禁忌长度和邻域大小分别取(n(n-1)/2)1/2和2n，其中n表示待决策订单的数量；经典IG算法中的参数分别取g=4，T=0.4；本文中的IGTA算法中的阈值和破坏因子分别取T0=n2，g=4。

具体来说，针对每个测试的问题实例，分别比较4种算法在不同实例上的求解效果，文中用最优目标均值(AVG)和最大值(MAX)来对算法的求解质量进行评估，以及使用标准差(STD)来评价算法的鲁棒性。此外对于某个问题规模下的测试实例l，考虑到算法会重复运行M次，本文定义了一个平均相对百分偏差(average relative percentage deviation，ARPD)来对各个规模下不同算法的性能进行评估，计算公式如(12)：

(12)

其中:TNRalg(l,m)表示对于给定算法alg在实例l下运行第m次所获得的目标值，TNRbest(l)表示在实例l下所有实验得到的最优目标值，L表示同规模问题下的测试实例之和。

在问题规模n=20情况下的仿真实验结果如表2所示。

由表2所示的实验结果比较分析可知：本文所提出的IGTA算法表现较好，在最优值的寻找方面均能找到不差于其余3种对比算法的解，在均值和标准差方面IGTA算法与经典IG算法求解效果相近。

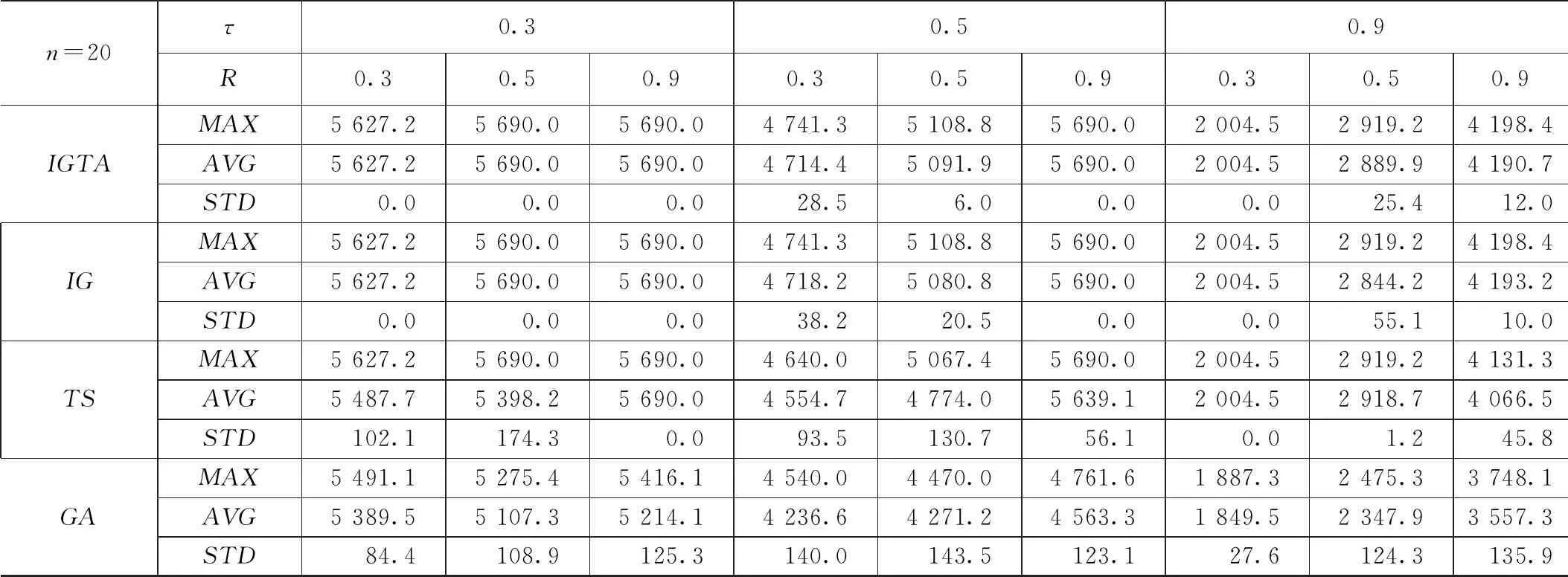
表2 n=20 时 4种算法的性能比较

在问题规模n=40和n=60情况下的仿真实验结果如表3和表4所示。由表3和表4中所列出的数据可以明显的看出随着订单规模的增加，改进的IG算法无论是在最优值的寻找还是整体均值的计算都能找到4种算法中最好的解。除此之外，从上表的STD对比中可以看出，本文提出的IGTA算法始终保持着比较稳定的状态，由此说明IGTA算法相比于其余3种算法具有更好的鲁棒性。

为了更加直观的展示4种算法在不同订单规模下的求解效果对比，本文通过提出一种平均相对偏差的评价指标可以更加清楚的看到在不同问题规模下的4种算法的差异，4种对比算法的总体ARPD对比柱状图如图2所示。

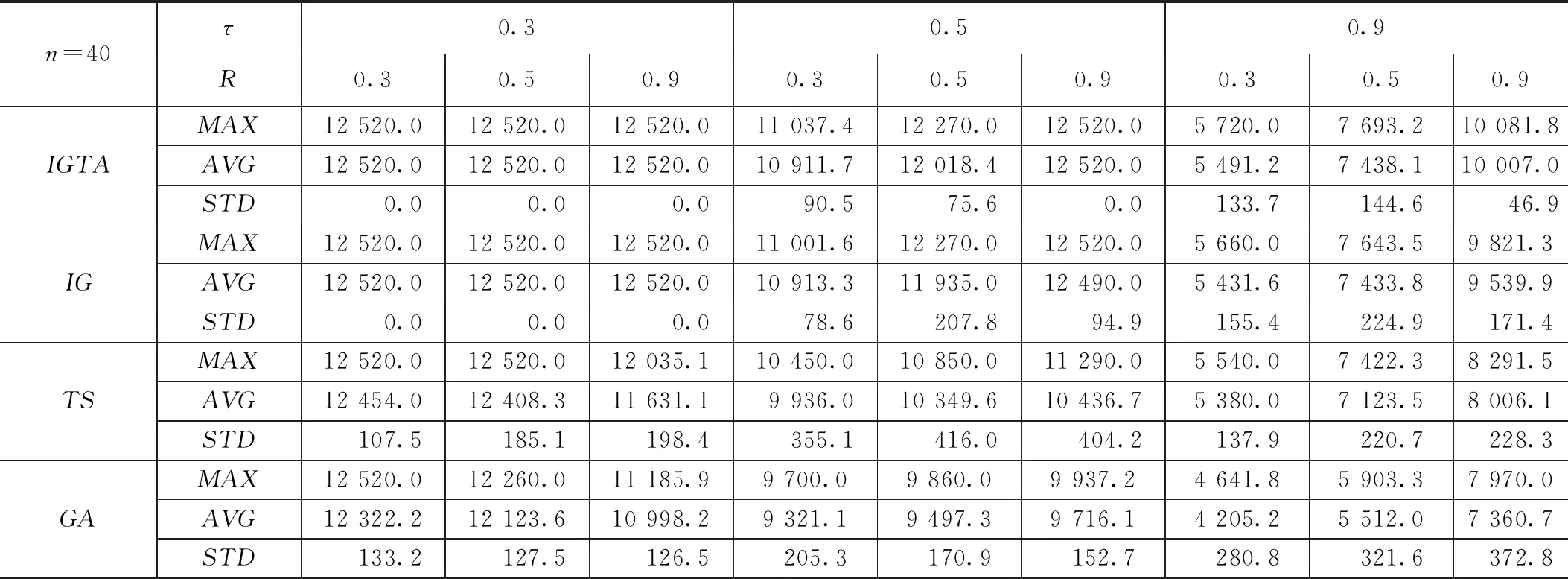
表3 n=40 时 4种算法的性能比较

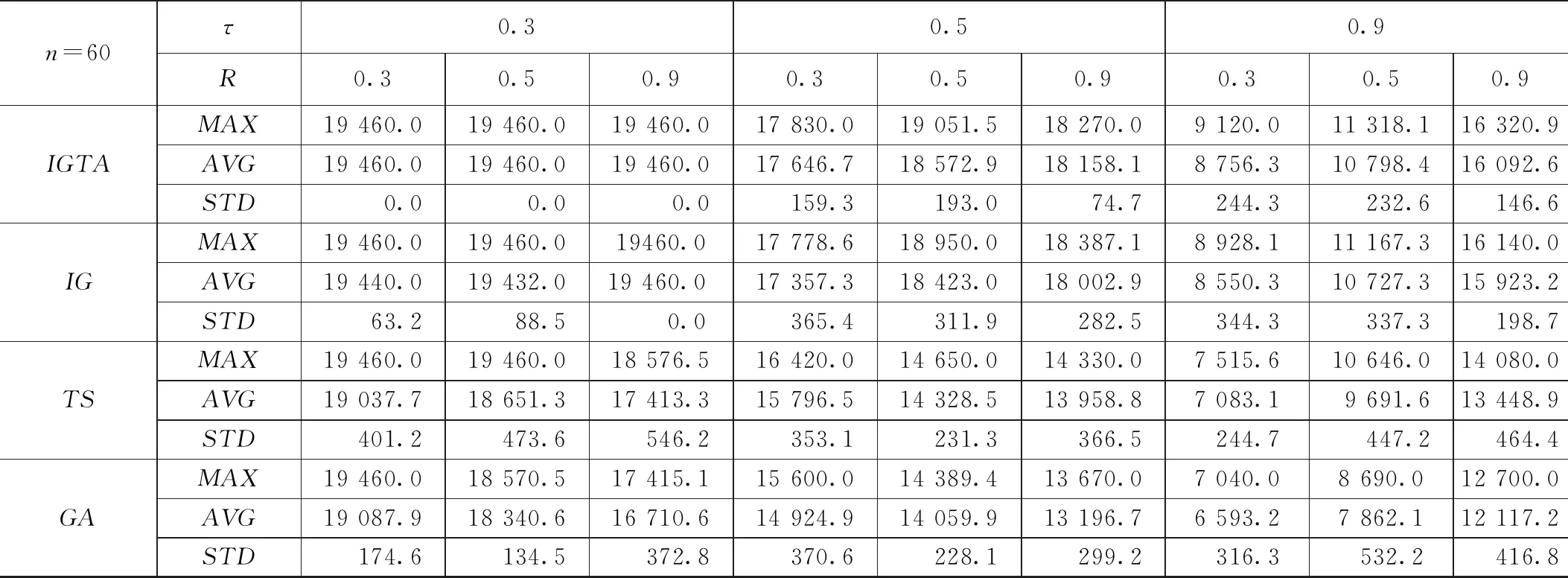
表4 n=60 时 4种算法的性能比较

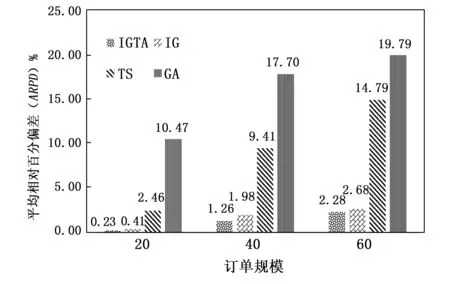
图2 4种算法在不同规模下的ARPD对比图

从图2中可以看出当订单规模为20的时候所有算法的ARPD值均很小，随着问题规模的增大，IGTA算法的ARPD值呈现出递增趋势。且在哪种订单规模下，统计上IGTA算法的ARPD值都是最小的，由此我们可以得出IGTA算法在小、中、大规模问题下的求解质量均优于其余3种对比算法。

5 结束语

本文针对预制流水车间的订单接受与调度问题，构建了线性整数规划模型，并通过提出一种改进的迭代贪婪算法来求解这一问题，并通过计算仿真的方式与经典IG，TS以及GA算法进行对比。结果通过最优目标值、目标均值、标准差以及平均相对百分偏差，4个性能评价指标进行对比分析，表明了本文提出的IGTA算法有良好的求解效果。下一步的研究可以对IGTA算法中的局部搜索作进一步改良以开发效率更高的预制流水车间的订单接受与调度模型的元启发式算法；同时，在未来的研究中可以将本文方法推广到汽车制造，钢生产等按订单进行生产的行业中。